平行四边形及特殊的平行四边形 复习[上学期]
文档属性
| 名称 | 平行四边形及特殊的平行四边形 复习[上学期] | 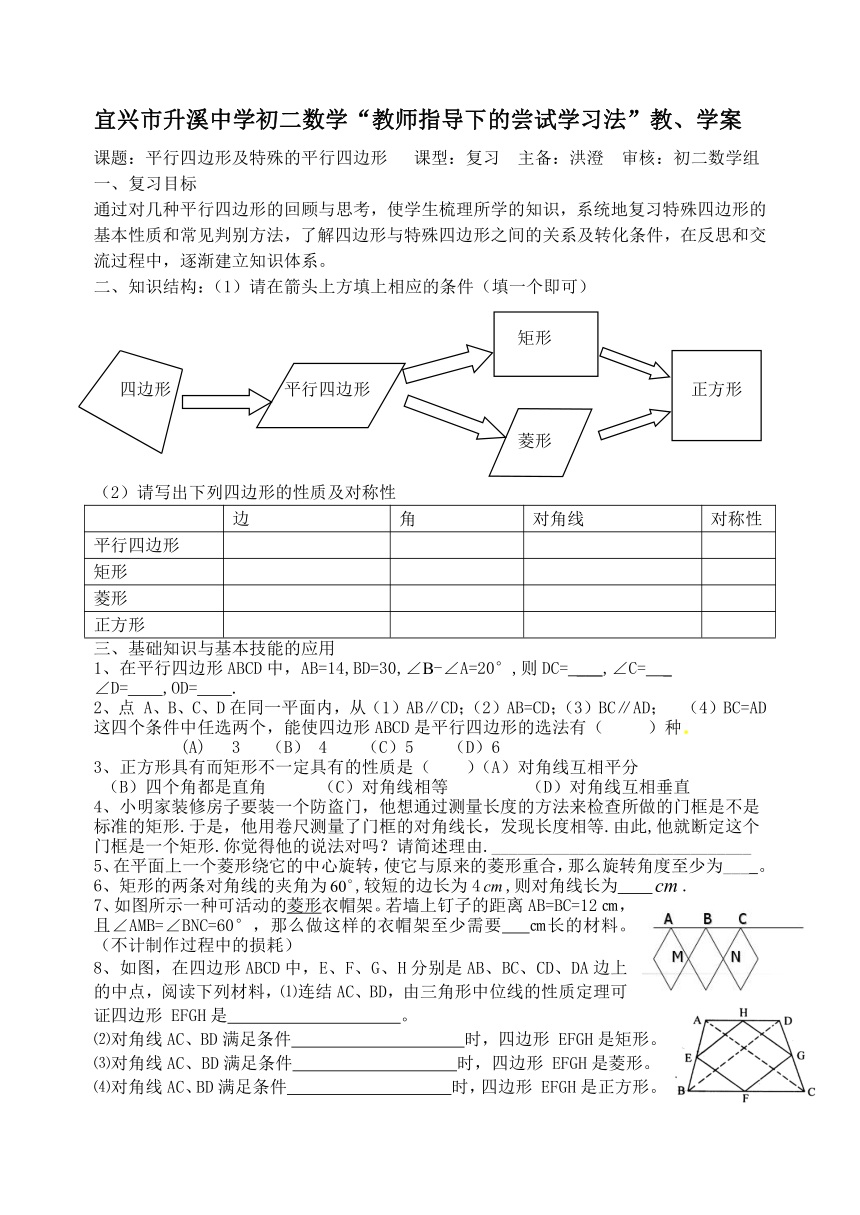 | |
| 格式 | rar | ||
| 文件大小 | 114.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-22 13:33:00 | ||
图片预览

文档简介
宜兴市升溪中学初二数学“教师指导下的尝试学习法”教、学案
课题:平行四边形及特殊的平行四边形 课型:复习 主备:洪澄 审核:初二数学组
1、 复习目标
通过对几种平行四边形的回顾与思考,使学生梳理所学的知识,系统地复习特殊四边形的基本性质和常见判别方法,了解四边形与特殊四边形之间的关系及转化条件,在反思和交流过程中,逐渐建立知识体系。
二、知识结构:(1)请在箭头上方填上相应的条件(填一个即可)
矩形
四边形 平行四边形 正方形
菱形
(2)请写出下列四边形的性质及对称性
边 角 对角线 对称性
平行四边形
矩形
菱形
正方形
三、基础知识与基本技能的应用
1、在平行四边形ABCD中,AB=14,BD=30,∠B-∠A=20°,则DC= ___,∠C= _
∠D= ,OD= .
2、点 A、B、C、D在同一平面内,从(1)AB∥CD;(2)AB=CD;(3)BC∥AD; (4)BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )种.
(A) 3 (B) 4 (C)5 (D)6
3、正方形具有而矩形不一定具有的性质是( )(A)对角线互相平分
(B)四个角都是直角 (C)对角线相等 (D)对角线互相垂直
4、小明家装修房子要装一个防盗门,他想通过测量长度的方法来检查所做的门框是不是标准的矩形.于是,他用卷尺测量了门框的对角线长,发现长度相等.由此,他就断定这个门框是一个矩形.你觉得他的说法对吗?请简述理由.______________________________
5、在平面上一个菱形绕它的中心旋转,使它与原来的菱形重合,那么旋转角度至少为___ 。
6、矩形的两条对角线的夹角为,较短的边长为4,则对角线长为 .
7、如图所示一种可活动的菱形衣帽架。若墙上钉子的距离AB=BC=12㎝,且∠AMB=∠BNC=60°,那么做这样的衣帽架至少需要 ㎝长的材料。(不计制作过程中的损耗)
8、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,⑴连结AC、BD,由三角形中位线的性质定理可证四边形 EFGH是 。
⑵对角线AC、BD满足条件 时,四边形 EFGH是矩形。
⑶对角线AC、BD满足条件 时,四边形 EFGH是菱形。
⑷对角线AC、BD满足条件 时,四边形 EFGH是正方形。
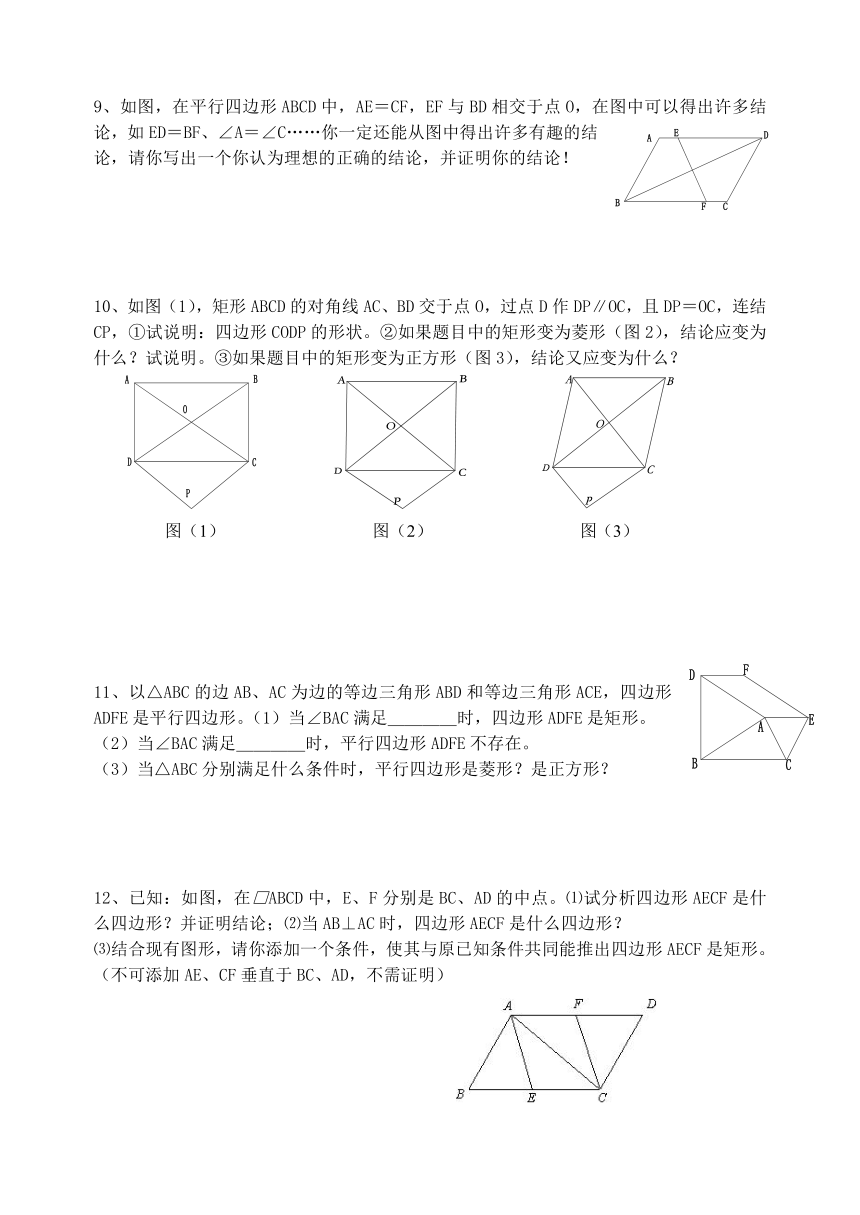
9、如图,在平行四边形ABCD中,AE=CF,EF与BD相交于点O,在图中可以得出许多结论,如ED=BF、∠A=∠C……你一定还能从图中得出许多有趣的结论,请你写出一个你认为理想的正确的结论,并证明你的结论!
10、如图(1),矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连结
CP,①试说明:四边形CODP的形状。②如果题目中的矩形变为菱形(图2),结论应变为什么?试说明。③如果题目中的矩形变为正方形(图3),结论又应变为什么?
11、以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形。(1)当∠BAC满足____时,四边形ADFE是矩形。
(2)当∠BAC满足____时,平行四边形ADFE不存在。
(3)当△ABC分别满足什么条件时,平行四边形是菱形?是正方形?
12、已知:如图,在□ABCD中,E、F分别是BC、AD的中点。⑴试分析四边形AECF是什么四边形?并证明结论;⑵当AB⊥AC时,四边形AECF是什么四边形?
⑶结合现有图形,请你添加一个条件,使其与原已知条件共同能推出四边形AECF是矩形。(不可添加AE、CF垂直于BC、AD,不需证明)
四、拓展与提高
1、下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是图形_____________(请填图形下面的代号)。
2、如图,有一块边长为4的正方形塑料模板ABCD,现将一块足够大的直角三角板的直角顶点落在A点上,两条直角边分别与CD交于F与CB延长线交于点E,则四边形AECF的面积是__。
3、如图菱形ABCD中,AB=2,∠BAD=60 ,E是AB的中点P是对角线AC上的一个动点,则PE+PB的 最 小值是____
4、如图已知,正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3,则EF等于( )A.7 B.5 C.4 D.3
已知:如图,在梯形中,,,,点自点向以的速度运动,到点即停止.点自点向以的速度运动,到点即停止,直线截梯形为两个四边形.问当,同时出发,几秒后其中一个四边形为平行四边形?
5、如图,在一张长12cm、宽5cm的矩形纸片上,要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),张丰同学沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到菱形AECF(见方案二).请你通过计算,比较李颖同学和张丰同学的折法,哪种菱形面积较大?
整合提高:
1、四边形ABCD中,∠A=∠C,∠B=∠D,则下列结论中不一定正确的是( )
A.AB=CD B.AD∥BC C.∠A=∠B D.对角线AC、BD互相平分
2、下列说法中,错误的是( )A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边形 C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形
3、如图,BD是菱形ABCD的一条对角线,∠ABD=65°,则∠A=____________.
4、如图,菱形ABCD的对角线长分别为2和5.P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于E,PF∥CD交AD于F.则阴影部分的面积是____________.
5、如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是中点四边形.如果AC=3,BD=4,那么A1B1C1D1的面积为
6、如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.(1)求∠2的度数.
(2)求证:BO=BE.
7、 如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且
CD=BF,以AD为一边作等边三角形ADE。①△ACD与△CBF是
全等三角形吗?说说你的理由。②四边形CDEF是平行四边形吗?
说说你的理由。
8、如图,O为矩形ABCD对角线交点,过O作EF⊥AC分别交AD,BC于F,E,若AB=2cm,BC=4cm.求四边形AECF的面积.
9、已知:如图,在正方形ABCD中,AC、BD交于点O,延长CB到点F,使 BF=BC
连结DF交AB于E.求证:OE=( )BF(在括号中填人一个适当的常数,再证明).
图(1)
图(2)
图(3)
图(1)
回答问题:
课题:平行四边形及特殊的平行四边形 课型:复习 主备:洪澄 审核:初二数学组
1、 复习目标
通过对几种平行四边形的回顾与思考,使学生梳理所学的知识,系统地复习特殊四边形的基本性质和常见判别方法,了解四边形与特殊四边形之间的关系及转化条件,在反思和交流过程中,逐渐建立知识体系。
二、知识结构:(1)请在箭头上方填上相应的条件(填一个即可)
矩形
四边形 平行四边形 正方形
菱形
(2)请写出下列四边形的性质及对称性
边 角 对角线 对称性
平行四边形
矩形
菱形
正方形
三、基础知识与基本技能的应用
1、在平行四边形ABCD中,AB=14,BD=30,∠B-∠A=20°,则DC= ___,∠C= _
∠D= ,OD= .
2、点 A、B、C、D在同一平面内,从(1)AB∥CD;(2)AB=CD;(3)BC∥AD; (4)BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )种.
(A) 3 (B) 4 (C)5 (D)6
3、正方形具有而矩形不一定具有的性质是( )(A)对角线互相平分
(B)四个角都是直角 (C)对角线相等 (D)对角线互相垂直
4、小明家装修房子要装一个防盗门,他想通过测量长度的方法来检查所做的门框是不是标准的矩形.于是,他用卷尺测量了门框的对角线长,发现长度相等.由此,他就断定这个门框是一个矩形.你觉得他的说法对吗?请简述理由.______________________________
5、在平面上一个菱形绕它的中心旋转,使它与原来的菱形重合,那么旋转角度至少为___ 。
6、矩形的两条对角线的夹角为,较短的边长为4,则对角线长为 .
7、如图所示一种可活动的菱形衣帽架。若墙上钉子的距离AB=BC=12㎝,且∠AMB=∠BNC=60°,那么做这样的衣帽架至少需要 ㎝长的材料。(不计制作过程中的损耗)
8、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,⑴连结AC、BD,由三角形中位线的性质定理可证四边形 EFGH是 。
⑵对角线AC、BD满足条件 时,四边形 EFGH是矩形。
⑶对角线AC、BD满足条件 时,四边形 EFGH是菱形。
⑷对角线AC、BD满足条件 时,四边形 EFGH是正方形。
9、如图,在平行四边形ABCD中,AE=CF,EF与BD相交于点O,在图中可以得出许多结论,如ED=BF、∠A=∠C……你一定还能从图中得出许多有趣的结论,请你写出一个你认为理想的正确的结论,并证明你的结论!
10、如图(1),矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连结
CP,①试说明:四边形CODP的形状。②如果题目中的矩形变为菱形(图2),结论应变为什么?试说明。③如果题目中的矩形变为正方形(图3),结论又应变为什么?
11、以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形。(1)当∠BAC满足____时,四边形ADFE是矩形。
(2)当∠BAC满足____时,平行四边形ADFE不存在。
(3)当△ABC分别满足什么条件时,平行四边形是菱形?是正方形?
12、已知:如图,在□ABCD中,E、F分别是BC、AD的中点。⑴试分析四边形AECF是什么四边形?并证明结论;⑵当AB⊥AC时,四边形AECF是什么四边形?
⑶结合现有图形,请你添加一个条件,使其与原已知条件共同能推出四边形AECF是矩形。(不可添加AE、CF垂直于BC、AD,不需证明)
四、拓展与提高
1、下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是图形_____________(请填图形下面的代号)。
2、如图,有一块边长为4的正方形塑料模板ABCD,现将一块足够大的直角三角板的直角顶点落在A点上,两条直角边分别与CD交于F与CB延长线交于点E,则四边形AECF的面积是__。
3、如图菱形ABCD中,AB=2,∠BAD=60 ,E是AB的中点P是对角线AC上的一个动点,则PE+PB的 最 小值是____
4、如图已知,正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3,则EF等于( )A.7 B.5 C.4 D.3
已知:如图,在梯形中,,,,点自点向以的速度运动,到点即停止.点自点向以的速度运动,到点即停止,直线截梯形为两个四边形.问当,同时出发,几秒后其中一个四边形为平行四边形?
5、如图,在一张长12cm、宽5cm的矩形纸片上,要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),张丰同学沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到菱形AECF(见方案二).请你通过计算,比较李颖同学和张丰同学的折法,哪种菱形面积较大?
整合提高:
1、四边形ABCD中,∠A=∠C,∠B=∠D,则下列结论中不一定正确的是( )
A.AB=CD B.AD∥BC C.∠A=∠B D.对角线AC、BD互相平分
2、下列说法中,错误的是( )A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边形 C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形
3、如图,BD是菱形ABCD的一条对角线,∠ABD=65°,则∠A=____________.
4、如图,菱形ABCD的对角线长分别为2和5.P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于E,PF∥CD交AD于F.则阴影部分的面积是____________.
5、如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是中点四边形.如果AC=3,BD=4,那么A1B1C1D1的面积为
6、如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.(1)求∠2的度数.
(2)求证:BO=BE.
7、 如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且
CD=BF,以AD为一边作等边三角形ADE。①△ACD与△CBF是
全等三角形吗?说说你的理由。②四边形CDEF是平行四边形吗?
说说你的理由。
8、如图,O为矩形ABCD对角线交点,过O作EF⊥AC分别交AD,BC于F,E,若AB=2cm,BC=4cm.求四边形AECF的面积.
9、已知:如图,在正方形ABCD中,AC、BD交于点O,延长CB到点F,使 BF=BC
连结DF交AB于E.求证:OE=( )BF(在括号中填人一个适当的常数,再证明).
图(1)
图(2)
图(3)
图(1)
回答问题:
