四川省绵阳市2022-2023学年高二下学期期末教学质量测试数学(理)试卷(Word版含答案)
文档属性
| 名称 | 四川省绵阳市2022-2023学年高二下学期期末教学质量测试数学(理)试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 555.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 12:39:02 | ||
图片预览




文档简介
秘密★启用前【考试时间:2023年7月7日14:10—16:10】
绵阳市2022-2023学年高二下学期期末教学质量测试
理科数学
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
l.已知i为虚数单位,复数z=i(3+i)在复平面内对应的点所在的象限为
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.命题p:“>1,>0”,则为
A.>1, B. ,
C.>1, D.,
3.袋中有黑、白两种颜色的球,从中进行有放回地摸球,用表示第一次摸得黑球,表
示第二次摸得黑球,则与是
A.相互独立事件 B.不相互独立事件 C.互斥事件 D.对立事件
4.的展开式中,项的系数为
A.-4 B.1 C. 6 D.12
5.函数的大致图象为
6.若函数,则“a>0”是“函数f(x)在(-2,0)上为减函数”的
A,充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.已知命题p:随机变量的方差=l,则=2;命题q:已知两个不同平面
,的法向量分别为,若=0,则.则下列命题中的真命题是
A. B. C. D.
8.第31届世界大学生夏季运动会,将于2023年7月28日在成都举办,是中国西部第一
次举办世界性综合运动会.某高校有甲,乙,丙,丁,戊5名翻译志愿者去参加A,B,C,D,E五个场馆的服务工作,每人服务一个场馆且每个场馆需要一人.由于特殊原因甲不去A场馆,乙不去B场馆,则不同的安排方法有
A. 120种 B.96种 C.78种 D、48种
9.若函数有两个不同的极值点,则实数a的取值范围为
A. a<-4 B.a>4 C.-44
10.在四棱锥P-ABCD中,底面ABCD 是菱形, PA平面ABCD,BAD=120°,PA=AD=2,
Q为棱PD上的一动点.则线段BQ长度的最小值为
A.3 B. C. D.
11.甲、乙两名游客慕名来到四川旅游,准备分别从九瘀沟、增眉山、海螺沟、都江堰、青城山这5个景点中随机选一个.事件A:甲和乙选择的景点不同,事件B:甲和乙恰好有一人选择九寨沟.则条件概率P(B/A)=
A. B. C. D、
12.己知,使得成立,其中m,n为常数且m<0,则下列结论正确的是
A、mn≤0 B、 C. D、
二、填空题:本大题共4小题,每小题5分,共20分。将答案填在答题卡相应位置。
13.已知复数z满足z(1-i)=4-2i (i为虚数单位),则|
14.若,则(用数字作答)
15.过点P(1,4)作曲线的切线,则切线方程为________.
16.已知函数在上为减函数,命题P:
为假命题,则k的最大值为___.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
某学校为筑牢校园安全防线,提升学生安全意识,举办了一次知识竞赛,以学生团队为单位参加比赛,每个团队每题作答正确得5分,错误得1分.已知甲队回答题库中三类相关知识题目正确率如下表:
(1)若甲队抽到交通安全、消防安全各一道题目,求甲队作答这两道题目后得分不低于6分的概率;
(2)已知甲队抽到3道题目,且类别均不相同,设甲队在作答完这3道题目后的总分为Y,求Y的分布列及数学期望.
18.(12分)
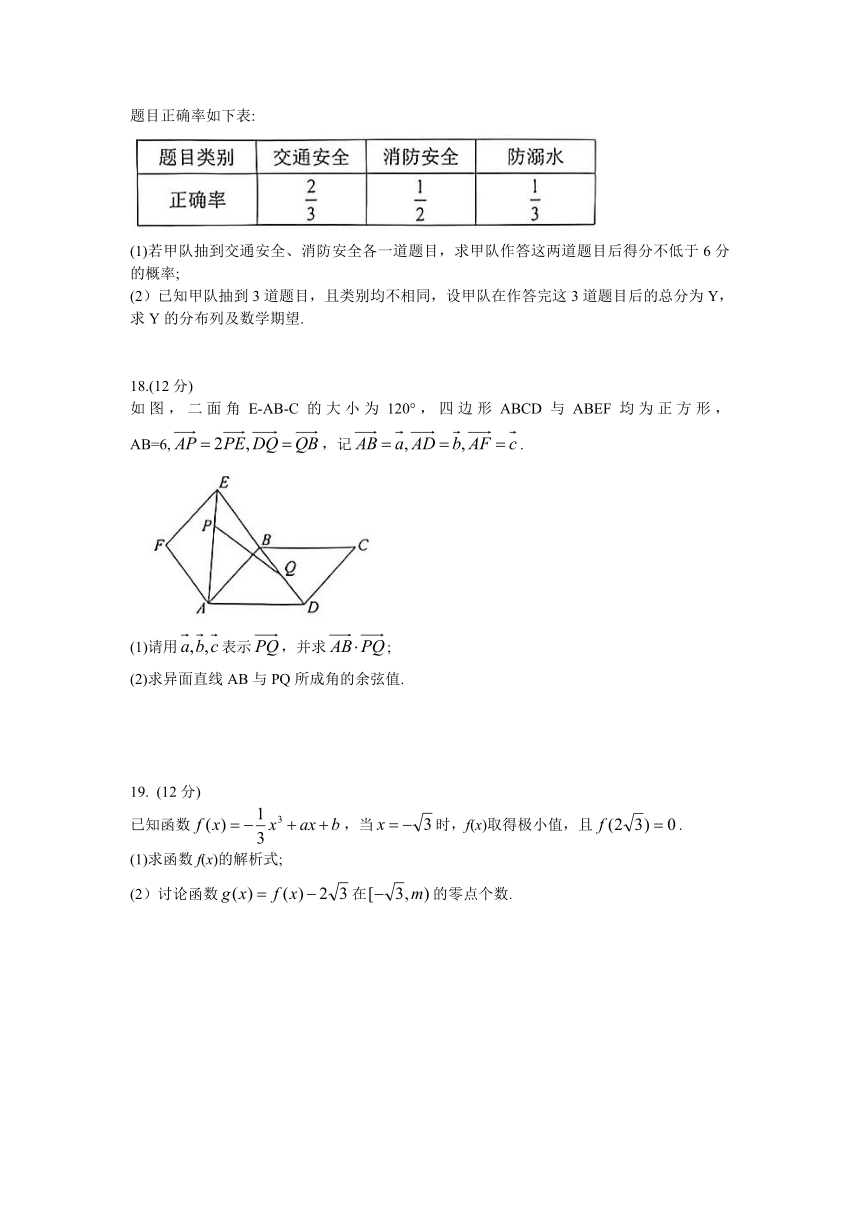
如图,二面角E-AB-C的大小为120°,四边形ABCD与ABEF均为正方形,AB=6,,记.
(1)请用表示,并求;
(2)求异面直线AB与PQ所成角的余弦值.
(12分)
已知函数,当时,f(x)取得极小值,且.
(1)求函数f(x)的解析式;
(2)讨论函数在的零点个数.
20.(12分)
如图,在多面体ABCDE中,平面ACD平面ABC,BE平面ABC,△ABC和△ACD均为正三角形,AC=2,,点M为棱CD上一点.
(1)求证:DE//平面ABC;
(2)若M为DC中点,求平面AMB与平面ACD所成锐二面角的余弦值.
21.(12分)
己知函数x -l
(1)当k=0时,求f(x)的单调性;
(2)若f(x)在上存在最小值,求实数k的取值范围.
(二)选考题:共10分。请考生在第22、23题中任选一题做答。如果多做,则按所做的第一题记分。
22.[选修44:坐标系与参数方程]( 10分)
在平面直角坐标系xOy中,曲线C1的参数方程为为参数),以坐标
原点О为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为,其中.
(1)求C1的普通方程与直线l的直角坐标方程;
(2)直线l与曲线C1交于A,B两点,且A,B两点对应的极角分别为,求的值.
23.「选修4—-5:不等式选讲](10分)
已知函数.
(1)当时,求不等式f(x)<4的解集;
(2)若函数f(x)的最小值为2,且,求的最小值.
绵阳市2022-2023学年高二下学期期末教学质量测试
理科数学参考答案及评分意见
一、选择题:本大题共12小题,每小题5分,共60分.
BDACD BCCAD AC
二、填空题:本大题共4小题,每小题5分,共20分.
13. 14.122 15. 16.2
三、解答题:本大题共6小题,共70分.
17.解:(1)设答对交通安全题目、答对消防安全题目的事件分别为,,
两道题目回答得分不低于6分的事件为B, 2分
则
, 4分
∴该队两道题目回答得分不低于6分的概率为; 5分
(2)X的可能取值为3,7,11,15, 6分
; 7分
; 8分
; 9分
, 10分
则Y的分布列为:
Y 3 7 11 15
P
11分
所以. 12分
18.解:(1)由已知得:=(a+c), 1分
=(a+b), 2分
∴b a c, 4分
∴a﹒(b a c)=a﹒b a2 a﹒c 5分
=0 -0 =-6; 6分
(2)由题意可得a·b=a·c=0, 7分
由(1)得,b a c,
∴(b a c)2
=b2+a2+c2-2××a·b-2××b·c+2××a·c 9分
=×36+×36+×36-0-2×××6×6×cos120 +0
=38
∴, 10分
∴===, 11分
∴异面直线AB与PQ所成角的余弦值为. 12分
19.解:(1)因为,所以, 1分
∵时,有极小值,
∴,即,即. 2分
当时,,令,即; 3分
令,即或,
∴在上单调递减,在上单调递增,在上单调递减,
∴在处取得极小值,符合题目条件. 4分
又,所以, 5分
∴. 6分
(2)由(1)可知,函数在上单调递减,
在上单调递增,在上单调递减, 7分
令,得,, 8分
①当时,则在上单调递增,,
∴在上无零点; 9分
②当时,则,则在上仅有一个零点, 10分
③当时,在上单调递减,,
∴在上有两个零点; 11分
综上所述,当时,在上无零点;
当时,在上仅有一个零点;
当时,在上有两个零点. 12分
20.解:(1)取AC中点O,连接DO、OB,
在正△ACD和正△ABC中,,
∴DO⊥AC,BO⊥AC,DO=BO=, 2分
而平面平面ABC,平面平面,
平面ACD,平面ABC,
∴平面ABC,平面ACD, 4分
又平面ABC,则有,而.
∴四边形DOBE是平行四边形,则, 5分
而平面ABC,平面ABC,
∴DE//平面ABC. 6分
(2)由(1)知,OB,OC,OD两两垂直,建立如图所示的空间直角坐标系O-xyz,
则A(0, 1,0),B(,0,0),D(0,0,),C(0,1,0),, 8分
∴,, 9分
显然平面DAC的一个法向量为, 10分
设平面MAB的一个法向量为,
则,令,得, 11分
,
∴平面AMB与平面ACD所成锐二面角的余弦值为. 12分
21.解:(1)由题,的定义域为, 1分
, 2分
令,则, 3分
∴当时,,为减函数,,;
当时,,为增函数,,; 4分
∴的单调递增区间为,. 5分
(2)令,
∴
, 7分
令,
; 8分
①当时,恒成立,则在上单调递增,
∴,即,则在上单调递增,
此时在上不存在最小值,不合题意; 9分
②当时,若,则;若,则;
∴在上单调递减,在上单调递增,
又,,又,
∴存在,使得,且当时,,即;
当时,,即; 10分
∴在上单调递减,在上单调递增,
∴,即存在最小值; 11分
综上所述:实数的取值范围为. 12分
22.解:(1)由,得,消去,
∴C的普通方程为; 2分
由,得,
令,,
∴直线的直角坐标方程为. 4分
(2)在中,令,,所以,
即C的极坐标方程为, 5分
联立,得, 6分
∴,所以, 7分
又,则,所以或或或,
解得或或或, 8分
由图可知,两交点位于第一、四象限,
∴或, 9分
∴. 10分
23.解:(1)当时,等价于, 1分
当时,,则, 2分
当时,,则, 3分
当时,,则, 4分
综上所述,不等式的解集为. 5分
(2)∵,
当且仅当等号成立,,即, 6分
∵,∴, 7分
∴, 8分
当且仅当,即,即,时,等号成立, 9分
∴的最小值为9. 10分
绵阳市2022-2023学年高二下学期期末教学质量测试
理科数学
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
l.已知i为虚数单位,复数z=i(3+i)在复平面内对应的点所在的象限为
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.命题p:“>1,>0”,则为
A.>1, B. ,
C.>1, D.,
3.袋中有黑、白两种颜色的球,从中进行有放回地摸球,用表示第一次摸得黑球,表
示第二次摸得黑球,则与是
A.相互独立事件 B.不相互独立事件 C.互斥事件 D.对立事件
4.的展开式中,项的系数为
A.-4 B.1 C. 6 D.12
5.函数的大致图象为
6.若函数,则“a>0”是“函数f(x)在(-2,0)上为减函数”的
A,充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.已知命题p:随机变量的方差=l,则=2;命题q:已知两个不同平面
,的法向量分别为,若=0,则.则下列命题中的真命题是
A. B. C. D.
8.第31届世界大学生夏季运动会,将于2023年7月28日在成都举办,是中国西部第一
次举办世界性综合运动会.某高校有甲,乙,丙,丁,戊5名翻译志愿者去参加A,B,C,D,E五个场馆的服务工作,每人服务一个场馆且每个场馆需要一人.由于特殊原因甲不去A场馆,乙不去B场馆,则不同的安排方法有
A. 120种 B.96种 C.78种 D、48种
9.若函数有两个不同的极值点,则实数a的取值范围为
A. a<-4 B.a>4 C.-4
10.在四棱锥P-ABCD中,底面ABCD 是菱形, PA平面ABCD,BAD=120°,PA=AD=2,
Q为棱PD上的一动点.则线段BQ长度的最小值为
A.3 B. C. D.
11.甲、乙两名游客慕名来到四川旅游,准备分别从九瘀沟、增眉山、海螺沟、都江堰、青城山这5个景点中随机选一个.事件A:甲和乙选择的景点不同,事件B:甲和乙恰好有一人选择九寨沟.则条件概率P(B/A)=
A. B. C. D、
12.己知,使得成立,其中m,n为常数且m<0,则下列结论正确的是
A、mn≤0 B、 C. D、
二、填空题:本大题共4小题,每小题5分,共20分。将答案填在答题卡相应位置。
13.已知复数z满足z(1-i)=4-2i (i为虚数单位),则|
14.若,则(用数字作答)
15.过点P(1,4)作曲线的切线,则切线方程为________.
16.已知函数在上为减函数,命题P:
为假命题,则k的最大值为___.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
某学校为筑牢校园安全防线,提升学生安全意识,举办了一次知识竞赛,以学生团队为单位参加比赛,每个团队每题作答正确得5分,错误得1分.已知甲队回答题库中三类相关知识题目正确率如下表:
(1)若甲队抽到交通安全、消防安全各一道题目,求甲队作答这两道题目后得分不低于6分的概率;
(2)已知甲队抽到3道题目,且类别均不相同,设甲队在作答完这3道题目后的总分为Y,求Y的分布列及数学期望.
18.(12分)
如图,二面角E-AB-C的大小为120°,四边形ABCD与ABEF均为正方形,AB=6,,记.
(1)请用表示,并求;
(2)求异面直线AB与PQ所成角的余弦值.
(12分)
已知函数,当时,f(x)取得极小值,且.
(1)求函数f(x)的解析式;
(2)讨论函数在的零点个数.
20.(12分)
如图,在多面体ABCDE中,平面ACD平面ABC,BE平面ABC,△ABC和△ACD均为正三角形,AC=2,,点M为棱CD上一点.
(1)求证:DE//平面ABC;
(2)若M为DC中点,求平面AMB与平面ACD所成锐二面角的余弦值.
21.(12分)
己知函数x -l
(1)当k=0时,求f(x)的单调性;
(2)若f(x)在上存在最小值,求实数k的取值范围.
(二)选考题:共10分。请考生在第22、23题中任选一题做答。如果多做,则按所做的第一题记分。
22.[选修44:坐标系与参数方程]( 10分)
在平面直角坐标系xOy中,曲线C1的参数方程为为参数),以坐标
原点О为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为,其中.
(1)求C1的普通方程与直线l的直角坐标方程;
(2)直线l与曲线C1交于A,B两点,且A,B两点对应的极角分别为,求的值.
23.「选修4—-5:不等式选讲](10分)
已知函数.
(1)当时,求不等式f(x)<4的解集;
(2)若函数f(x)的最小值为2,且,求的最小值.
绵阳市2022-2023学年高二下学期期末教学质量测试
理科数学参考答案及评分意见
一、选择题:本大题共12小题,每小题5分,共60分.
BDACD BCCAD AC
二、填空题:本大题共4小题,每小题5分,共20分.
13. 14.122 15. 16.2
三、解答题:本大题共6小题,共70分.
17.解:(1)设答对交通安全题目、答对消防安全题目的事件分别为,,
两道题目回答得分不低于6分的事件为B, 2分
则
, 4分
∴该队两道题目回答得分不低于6分的概率为; 5分
(2)X的可能取值为3,7,11,15, 6分
; 7分
; 8分
; 9分
, 10分
则Y的分布列为:
Y 3 7 11 15
P
11分
所以. 12分
18.解:(1)由已知得:=(a+c), 1分
=(a+b), 2分
∴b a c, 4分
∴a﹒(b a c)=a﹒b a2 a﹒c 5分
=0 -0 =-6; 6分
(2)由题意可得a·b=a·c=0, 7分
由(1)得,b a c,
∴(b a c)2
=b2+a2+c2-2××a·b-2××b·c+2××a·c 9分
=×36+×36+×36-0-2×××6×6×cos120 +0
=38
∴, 10分
∴===, 11分
∴异面直线AB与PQ所成角的余弦值为. 12分
19.解:(1)因为,所以, 1分
∵时,有极小值,
∴,即,即. 2分
当时,,令,即; 3分
令,即或,
∴在上单调递减,在上单调递增,在上单调递减,
∴在处取得极小值,符合题目条件. 4分
又,所以, 5分
∴. 6分
(2)由(1)可知,函数在上单调递减,
在上单调递增,在上单调递减, 7分
令,得,, 8分
①当时,则在上单调递增,,
∴在上无零点; 9分
②当时,则,则在上仅有一个零点, 10分
③当时,在上单调递减,,
∴在上有两个零点; 11分
综上所述,当时,在上无零点;
当时,在上仅有一个零点;
当时,在上有两个零点. 12分
20.解:(1)取AC中点O,连接DO、OB,
在正△ACD和正△ABC中,,
∴DO⊥AC,BO⊥AC,DO=BO=, 2分
而平面平面ABC,平面平面,
平面ACD,平面ABC,
∴平面ABC,平面ACD, 4分
又平面ABC,则有,而.
∴四边形DOBE是平行四边形,则, 5分
而平面ABC,平面ABC,
∴DE//平面ABC. 6分
(2)由(1)知,OB,OC,OD两两垂直,建立如图所示的空间直角坐标系O-xyz,
则A(0, 1,0),B(,0,0),D(0,0,),C(0,1,0),, 8分
∴,, 9分
显然平面DAC的一个法向量为, 10分
设平面MAB的一个法向量为,
则,令,得, 11分
,
∴平面AMB与平面ACD所成锐二面角的余弦值为. 12分
21.解:(1)由题,的定义域为, 1分
, 2分
令,则, 3分
∴当时,,为减函数,,;
当时,,为增函数,,; 4分
∴的单调递增区间为,. 5分
(2)令,
∴
, 7分
令,
; 8分
①当时,恒成立,则在上单调递增,
∴,即,则在上单调递增,
此时在上不存在最小值,不合题意; 9分
②当时,若,则;若,则;
∴在上单调递减,在上单调递增,
又,,又,
∴存在,使得,且当时,,即;
当时,,即; 10分
∴在上单调递减,在上单调递增,
∴,即存在最小值; 11分
综上所述:实数的取值范围为. 12分
22.解:(1)由,得,消去,
∴C的普通方程为; 2分
由,得,
令,,
∴直线的直角坐标方程为. 4分
(2)在中,令,,所以,
即C的极坐标方程为, 5分
联立,得, 6分
∴,所以, 7分
又,则,所以或或或,
解得或或或, 8分
由图可知,两交点位于第一、四象限,
∴或, 9分
∴. 10分
23.解:(1)当时,等价于, 1分
当时,,则, 2分
当时,,则, 3分
当时,,则, 4分
综上所述,不等式的解集为. 5分
(2)∵,
当且仅当等号成立,,即, 6分
∵,∴, 7分
∴, 8分
当且仅当,即,即,时,等号成立, 9分
∴的最小值为9. 10分
同课章节目录
