12.2 全等三角形的判定同步练习题(含答案)
文档属性
| 名称 | 12.2 全等三角形的判定同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 18:13:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.2全等三角形的判定
一、选择题
根据下列条件,能画出形状、大小确定的三角形的是
A. ,
B. ,,
C. ,,
D. ,,
如图,已知 ,,如果要说明 ,那么还可以补充的条件是
A. B. C. D.
为测量池塘两端 , 的距离,小王设计了如下方案:如图,先在平地上取一个可以直接到达 , 的点 ,再连接 ,,并分别延长至点 ,,使得 ,,由 得到 ,所以测出 的长即为 , 的距离,那么判定 的理由是
A.边边边 B.边角边 C.角边角 D.角角边
如图,已知 ,,增加下列条件:;;;,其中能使 的条件的个数是
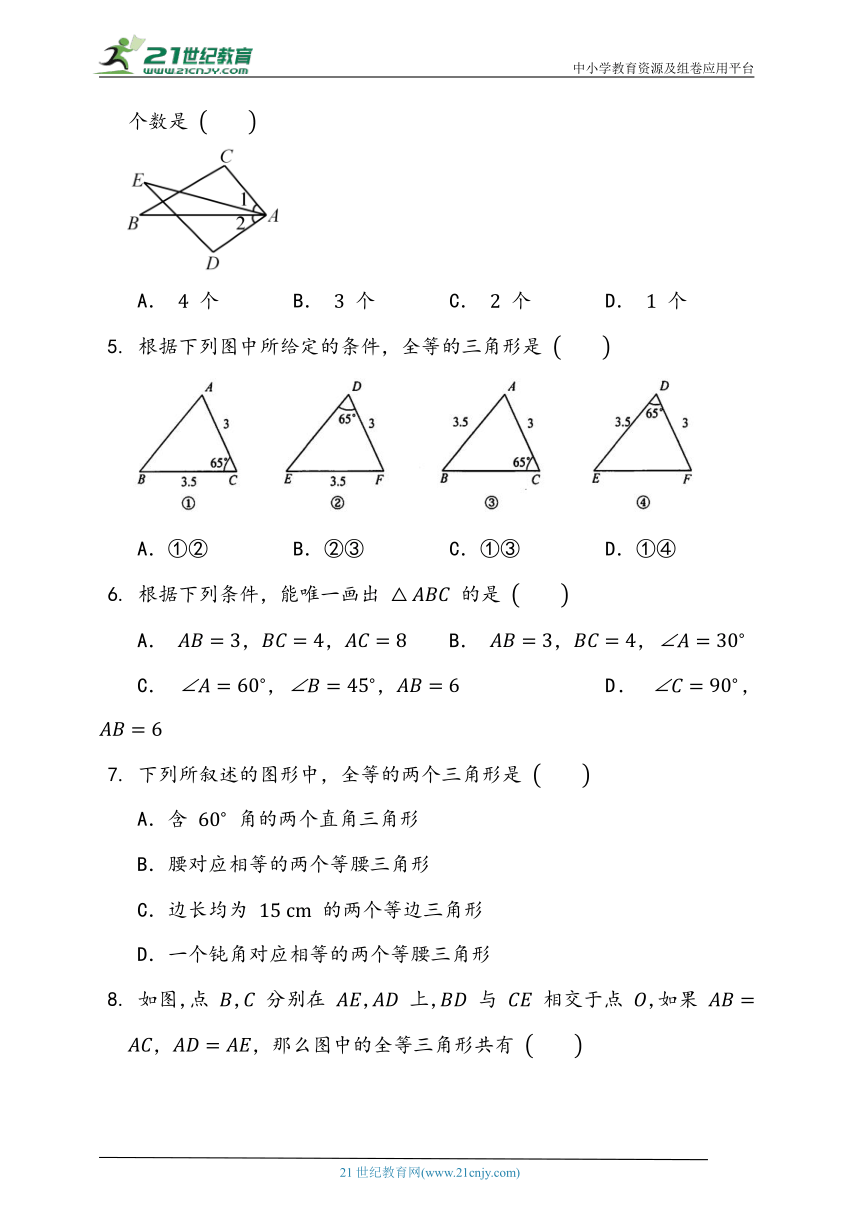
A. 个 B. 个 C. 个 D. 个
根据下列图中所给定的条件,全等的三角形是
A.①② B.②③ C.①③ D.①④
根据下列条件,能唯一画出 的是
A. ,, B. ,,
C. ,, D. ,
下列所叙述的图形中,全等的两个三角形是
A.含 角的两个直角三角形
B.腰对应相等的两个等腰三角形
C.边长均为 的两个等边三角形
D.一个钝角对应相等的两个等腰三角形
如图,点 , 分别在 , 上, 与 相交于点 ,如果 ,,那么图中的全等三角形共有
A. 对 B. 对 C. 对 D. 对
二、填空题
如图,如果 ,,,那么 ,理由 ,所以 , .
如图,点 ,,, 在同一直线上,已知 ,,添加条件 ,可以判定 ,判定理由是 ;也可添加条件 ,可以判定 ,判定理由是 .
如图所示,已知 ,,要推得 ,若以" "为依据,还缺条件 .
如图所示的两个三角形 全等.(填“一定”或“不一定”)
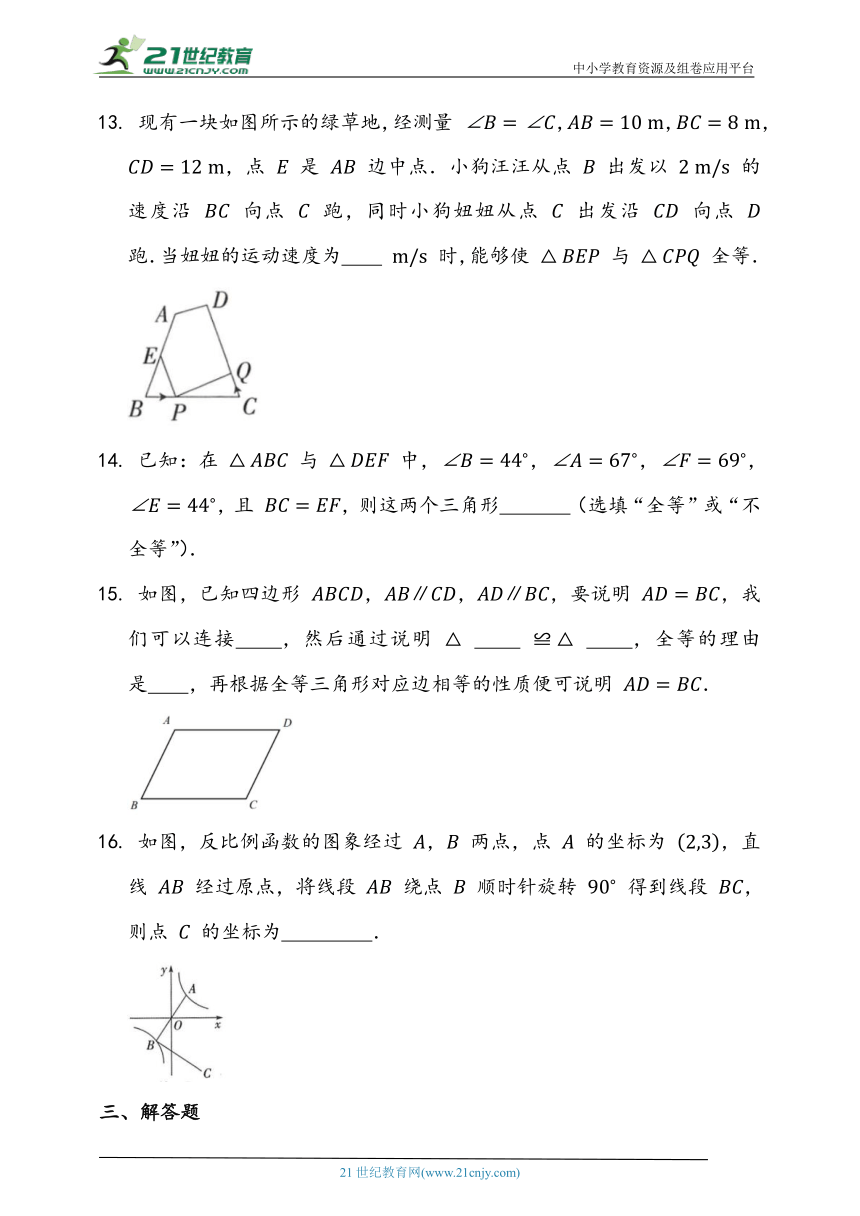
现有一块如图所示的绿草地,经测量 ,,,,点 是 边中点.小狗汪汪从点 出发以 的速度沿 向点 跑,同时小狗妞妞从点 出发沿 向点 跑.当妞妞的运动速度为 时,能够使 与 全等.
已知:在 与 中,,,,,且 ,则这两个三角形 (选填“全等”或“不全等”).
如图,已知四边形 ,,,要说明 ,我们可以连接 ,然后通过说明 ,全等的理由是 ,再根据全等三角形对应边相等的性质便可说明 .
如图,反比例函数的图象经过 , 两点,点 的坐标为 ,直线 经过原点,将线段 绕点 顺时针旋转 得到线段 ,则点 的坐标为 .
三、解答题
在 中,,, 为 延长线上一点,点 在 上,且 .
(1) 求证:;
(2) 若 ,求 度数.
如图,在四边形 中, 与 相交于点 , 为 上一点,且 ,.
(1) 说明 与 全等的理由;
(2) 说明 与 全等的理由.
如图,,,.
说明:
(1) 的理由;
的理由.
如图,在 和 中,点 ,,, 在同一条直线上,有下面四个论断:① ;② ;③ ;④ .请用其中的 个作为条件,余下的一个作为结论,编写一道几何题,并加以证明.
答案
一、选择题
1. 【答案】C
2. 【答案】B
3. 【答案】B
4. 【答案】B
5. 【答案】D
6. 【答案】C
7. 【答案】C
8. 【答案】C
二、填空题
9. 【答案】 ; ; ;
10. 【答案】 ; ; ;
11. 【答案】
12. 【答案】一定
13. 【答案】 或
【解析】设点 运动的时间为 ,则 ,,
,
分情况求解如下:
①当 , 时,,
即有 ,解得 ,
,
此时妞妞的运动速度为 ;
②当 , 时,,
即有 ,解得 ,
此时妞妞的运动速度为 .
故答案为 或 .
14. 【答案】全等
15. 【答案】 或 ; 或 ; 或 ; 或
16. 【答案】
三、解答题
17. 【答案】
(1) ,
.
在 和 中,
.
(2) ,,
.
,由(1)知 ,
,
.
18. 【答案】
(1) 因为 (已知),
又因为 (邻补角的意义),
所以 (等式性质).
在 和 中,
所以 .
(2) 因为 ,
所以 (全等三角形对应边相等),(全等三角形对应角相等),
在 与 中,
所以 .
19. 【答案】
(1) 先证 ,
,
.
(2) 证 ,可得 .
20. 【答案】可编题一:已知①②④,求证③.证明如下:
,
,即 .
,
.
在 和 中,
,
.
可编题二:已知②③④,求证①.可用 证明 .
可编题三:已知①③④,求证②.可用 证明 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
12.2全等三角形的判定
一、选择题
根据下列条件,能画出形状、大小确定的三角形的是
A. ,
B. ,,
C. ,,
D. ,,
如图,已知 ,,如果要说明 ,那么还可以补充的条件是
A. B. C. D.
为测量池塘两端 , 的距离,小王设计了如下方案:如图,先在平地上取一个可以直接到达 , 的点 ,再连接 ,,并分别延长至点 ,,使得 ,,由 得到 ,所以测出 的长即为 , 的距离,那么判定 的理由是
A.边边边 B.边角边 C.角边角 D.角角边
如图,已知 ,,增加下列条件:;;;,其中能使 的条件的个数是
A. 个 B. 个 C. 个 D. 个
根据下列图中所给定的条件,全等的三角形是
A.①② B.②③ C.①③ D.①④
根据下列条件,能唯一画出 的是
A. ,, B. ,,
C. ,, D. ,
下列所叙述的图形中,全等的两个三角形是
A.含 角的两个直角三角形
B.腰对应相等的两个等腰三角形
C.边长均为 的两个等边三角形
D.一个钝角对应相等的两个等腰三角形
如图,点 , 分别在 , 上, 与 相交于点 ,如果 ,,那么图中的全等三角形共有
A. 对 B. 对 C. 对 D. 对
二、填空题
如图,如果 ,,,那么 ,理由 ,所以 , .
如图,点 ,,, 在同一直线上,已知 ,,添加条件 ,可以判定 ,判定理由是 ;也可添加条件 ,可以判定 ,判定理由是 .
如图所示,已知 ,,要推得 ,若以" "为依据,还缺条件 .
如图所示的两个三角形 全等.(填“一定”或“不一定”)
现有一块如图所示的绿草地,经测量 ,,,,点 是 边中点.小狗汪汪从点 出发以 的速度沿 向点 跑,同时小狗妞妞从点 出发沿 向点 跑.当妞妞的运动速度为 时,能够使 与 全等.
已知:在 与 中,,,,,且 ,则这两个三角形 (选填“全等”或“不全等”).
如图,已知四边形 ,,,要说明 ,我们可以连接 ,然后通过说明 ,全等的理由是 ,再根据全等三角形对应边相等的性质便可说明 .
如图,反比例函数的图象经过 , 两点,点 的坐标为 ,直线 经过原点,将线段 绕点 顺时针旋转 得到线段 ,则点 的坐标为 .
三、解答题
在 中,,, 为 延长线上一点,点 在 上,且 .
(1) 求证:;
(2) 若 ,求 度数.
如图,在四边形 中, 与 相交于点 , 为 上一点,且 ,.
(1) 说明 与 全等的理由;
(2) 说明 与 全等的理由.
如图,,,.
说明:
(1) 的理由;
的理由.
如图,在 和 中,点 ,,, 在同一条直线上,有下面四个论断:① ;② ;③ ;④ .请用其中的 个作为条件,余下的一个作为结论,编写一道几何题,并加以证明.
答案
一、选择题
1. 【答案】C
2. 【答案】B
3. 【答案】B
4. 【答案】B
5. 【答案】D
6. 【答案】C
7. 【答案】C
8. 【答案】C
二、填空题
9. 【答案】 ; ; ;
10. 【答案】 ; ; ;
11. 【答案】
12. 【答案】一定
13. 【答案】 或
【解析】设点 运动的时间为 ,则 ,,
,
分情况求解如下:
①当 , 时,,
即有 ,解得 ,
,
此时妞妞的运动速度为 ;
②当 , 时,,
即有 ,解得 ,
此时妞妞的运动速度为 .
故答案为 或 .
14. 【答案】全等
15. 【答案】 或 ; 或 ; 或 ; 或
16. 【答案】
三、解答题
17. 【答案】
(1) ,
.
在 和 中,
.
(2) ,,
.
,由(1)知 ,
,
.
18. 【答案】
(1) 因为 (已知),
又因为 (邻补角的意义),
所以 (等式性质).
在 和 中,
所以 .
(2) 因为 ,
所以 (全等三角形对应边相等),(全等三角形对应角相等),
在 与 中,
所以 .
19. 【答案】
(1) 先证 ,
,
.
(2) 证 ,可得 .
20. 【答案】可编题一:已知①②④,求证③.证明如下:
,
,即 .
,
.
在 和 中,
,
.
可编题二:已知②③④,求证①.可用 证明 .
可编题三:已知①③④,求证②.可用 证明 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
