沪科版数学九年级上册 22.3 相似三角形的性质(第3课时)同步练习(含答案)
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质(第3课时)同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 17:58:08 | ||
图片预览


文档简介
第3课时 相似三角形的性质(3)
1.两个正方形,其中一个正方形的边长为a,另一个正方形的边长为b,则两个正方形的对角线长的比为( )
A. B. C. D.
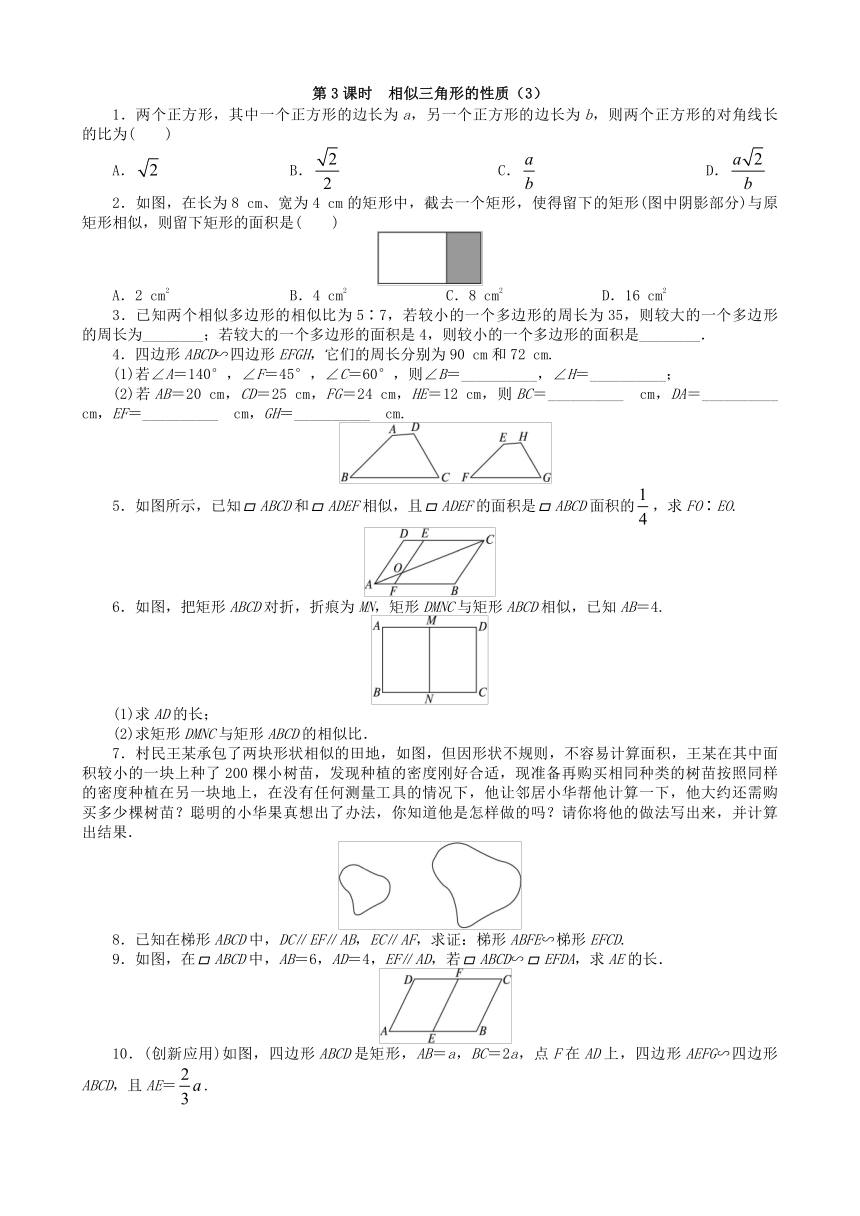
2.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
3.已知两个相似多边形的相似比为5∶7,若较小的一个多边形的周长为35,则较大的一个多边形的周长为________;若较大的一个多边形的面积是4,则较小的一个多边形的面积是________.
4.四边形ABCD∽四边形EFGH,它们的周长分别为90 cm和72 cm.
(1)若∠A=140°,∠F=45°,∠C=60°,则∠B=__________,∠H=__________;
(2)若AB=20 cm,CD=25 cm,FG=24 cm,HE=12 cm,则BC=__________ cm,DA=__________ cm,EF=__________ cm,GH=__________ cm.
5.如图所示,已知ABCD和ADEF相似,且ADEF的面积是ABCD面积的,求FO∶EO.
6.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
7.村民王某承包了两块形状相似的田地,如图,但因形状不规则,不容易计算面积,王某在其中面积较小的一块上种了200棵小树苗,发现种植的密度刚好合适,现准备再购买相同种类的树苗按照同样的密度种植在另一块地上,在没有任何测量工具的情况下,他让邻居小华帮他计算一下,他大约还需购买多少棵树苗?聪明的小华果真想出了办法,你知道他是怎样做的吗?请你将他的做法写出来,并计算出结果.
8.已知在梯形ABCD中,DC∥EF∥AB,EC∥AF,求证:梯形ABFE∽梯形EFCD.
9.如图,在ABCD中,AB=6,AD=4,EF∥AD,若ABCD∽EFDA,求AE的长.
10.(创新应用)如图,四边形ABCD是矩形,AB=a,BC=2a,点F在AD上,四边形AEFG∽四边形ABCD,且AE=.
(1)求AG的长;
(2)求证:△ABE∽△ADG;
(3)如果S矩形ABCD=630 cm2,求S矩形AEFG.
参考答案
1答案:C
2解析:因为阴影部分的矩形与原矩形相似,故阴影部分矩形的边长4应与原矩形的边长8为对应边,所以两矩形的相似比为1∶2,所以阴影部分的面积为×32=8(cm2).
答案:C
3答案:49
4答案:(1)45° 115° (2)30 15 16 20
5解:∵ABCD和ADEF相似,且ADEF的面积是ABCD的面积的,∴==.
∴CD=2AD=4AF.
又DE=AF,∴CE=3AF.
∵AB∥CD,∴△AOF∽△COE.
∴FO∶EO=AF∶CE=1∶3.
6解:(1)由已知,得MN=AB,MD==.
∵矩形DMNC与矩形ABCD相似,∴.∴=AB2.∴由AB=4,得AD=.
(2)矩形DMNC与矩形ABCD的相似比为.
7解:小华以相同的速度绕着这两块地走了一圈,分别用了20分钟和40分钟,说明这两块地的周长的比值等于20∶40=1∶2,又因为相似多边形面积的比值等于相似比的平方,所以这两块地的面积的比值等于1∶4.所以大块田地上种植的树苗的棵数是小块田地上的4倍,小华建议王某再购买800棵树苗比较合适.
8证明:∵CD∥FE,CE∥FA,∴∠D=∠FEA,∠CED=∠FAE.
∴△CDE∽△FEA.
同理可得△CFE∽△FBA.
∴,.
∵CD∥EF∥AB,
∴四边形CFED,FBAE分别是梯形.
∵∠D=∠FEA,∠FED=∠BAE,∠FCD=∠BFE,∠CFE=∠B, ,
∴梯形ABFE∽梯形EFCD.
9解:∵EF∥AD,四边形ABCD是平行四边形,AD=4,∴EF=AD=4.
∵ABCD∽EFDA,∴.
又∵AB=6,∴.
∴AE=.
10(1)解:∵四边形ABCD是矩形,且四边形AEFG∽四边形ABCD,
∴四边形AEFG是矩形.
∴.
∵AE=,AB=a,AD=2a,∴AG=.
(2)证明:由(1)知,∠1+∠3=∠2+∠3=90°,
∴∠1=∠2.
又∵,
∴△ABE∽△ADG.
(3)解:∵,
且S矩形ABCD=630,
∴S矩形AEFG=280(cm2).
1.两个正方形,其中一个正方形的边长为a,另一个正方形的边长为b,则两个正方形的对角线长的比为( )
A. B. C. D.
2.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
3.已知两个相似多边形的相似比为5∶7,若较小的一个多边形的周长为35,则较大的一个多边形的周长为________;若较大的一个多边形的面积是4,则较小的一个多边形的面积是________.
4.四边形ABCD∽四边形EFGH,它们的周长分别为90 cm和72 cm.
(1)若∠A=140°,∠F=45°,∠C=60°,则∠B=__________,∠H=__________;
(2)若AB=20 cm,CD=25 cm,FG=24 cm,HE=12 cm,则BC=__________ cm,DA=__________ cm,EF=__________ cm,GH=__________ cm.
5.如图所示,已知ABCD和ADEF相似,且ADEF的面积是ABCD面积的,求FO∶EO.
6.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
7.村民王某承包了两块形状相似的田地,如图,但因形状不规则,不容易计算面积,王某在其中面积较小的一块上种了200棵小树苗,发现种植的密度刚好合适,现准备再购买相同种类的树苗按照同样的密度种植在另一块地上,在没有任何测量工具的情况下,他让邻居小华帮他计算一下,他大约还需购买多少棵树苗?聪明的小华果真想出了办法,你知道他是怎样做的吗?请你将他的做法写出来,并计算出结果.
8.已知在梯形ABCD中,DC∥EF∥AB,EC∥AF,求证:梯形ABFE∽梯形EFCD.
9.如图,在ABCD中,AB=6,AD=4,EF∥AD,若ABCD∽EFDA,求AE的长.
10.(创新应用)如图,四边形ABCD是矩形,AB=a,BC=2a,点F在AD上,四边形AEFG∽四边形ABCD,且AE=.
(1)求AG的长;
(2)求证:△ABE∽△ADG;
(3)如果S矩形ABCD=630 cm2,求S矩形AEFG.
参考答案
1答案:C
2解析:因为阴影部分的矩形与原矩形相似,故阴影部分矩形的边长4应与原矩形的边长8为对应边,所以两矩形的相似比为1∶2,所以阴影部分的面积为×32=8(cm2).
答案:C
3答案:49
4答案:(1)45° 115° (2)30 15 16 20
5解:∵ABCD和ADEF相似,且ADEF的面积是ABCD的面积的,∴==.
∴CD=2AD=4AF.
又DE=AF,∴CE=3AF.
∵AB∥CD,∴△AOF∽△COE.
∴FO∶EO=AF∶CE=1∶3.
6解:(1)由已知,得MN=AB,MD==.
∵矩形DMNC与矩形ABCD相似,∴.∴=AB2.∴由AB=4,得AD=.
(2)矩形DMNC与矩形ABCD的相似比为.
7解:小华以相同的速度绕着这两块地走了一圈,分别用了20分钟和40分钟,说明这两块地的周长的比值等于20∶40=1∶2,又因为相似多边形面积的比值等于相似比的平方,所以这两块地的面积的比值等于1∶4.所以大块田地上种植的树苗的棵数是小块田地上的4倍,小华建议王某再购买800棵树苗比较合适.
8证明:∵CD∥FE,CE∥FA,∴∠D=∠FEA,∠CED=∠FAE.
∴△CDE∽△FEA.
同理可得△CFE∽△FBA.
∴,.
∵CD∥EF∥AB,
∴四边形CFED,FBAE分别是梯形.
∵∠D=∠FEA,∠FED=∠BAE,∠FCD=∠BFE,∠CFE=∠B, ,
∴梯形ABFE∽梯形EFCD.
9解:∵EF∥AD,四边形ABCD是平行四边形,AD=4,∴EF=AD=4.
∵ABCD∽EFDA,∴.
又∵AB=6,∴.
∴AE=.
10(1)解:∵四边形ABCD是矩形,且四边形AEFG∽四边形ABCD,
∴四边形AEFG是矩形.
∴.
∵AE=,AB=a,AD=2a,∴AG=.
(2)证明:由(1)知,∠1+∠3=∠2+∠3=90°,
∴∠1=∠2.
又∵,
∴△ABE∽△ADG.
(3)解:∵,
且S矩形ABCD=630,
∴S矩形AEFG=280(cm2).
