第七章 随机变量及其分布 章末小结 课件(共41张PPT)
文档属性
| 名称 | 第七章 随机变量及其分布 章末小结 课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 13:45:07 | ||
图片预览










文档简介
(共41张PPT)
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
章末复习与小结
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
学习内容
01 知识归纳
02 应用提升
03 对接高考
04 要点突破
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
学习目标
1.厘清随机变量及其分布;
2.筑牢章节知识体系;
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
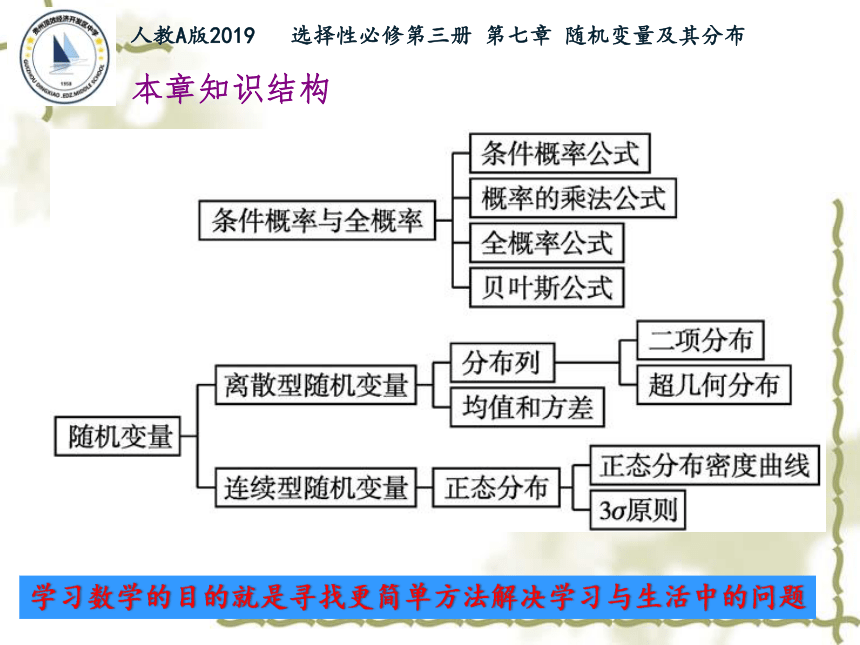
本章知识结构
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
条件概率是学习相互独立事件的前提和基础,计算条件概率时必须弄清要求的条件概率是在什么条件下发生的概率。
条件概率与全概率
解决条件概率问题,主要有以下几种方法:
(1)利用公式 计算;
(2)针对古典概型,可通过缩减基本事件总数求解。
(3)注意公式 的应用。
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
条件概率与全概率
解决全概率问题,主要有以下几种方法:
(1)结合古典概型与条件概率,厘清所求概率的含义。
(2)全概率公式
(3)注意公式的意义
(贝叶斯公式)
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
离散型随机变量及其分布列
X的概率分布列,简称分布列:
(1)利用公式 计算;列表表示。
(2)性质: 。
厘清所解决问题含义,准确确定变量取值
X服从两点分布,或0-1分布:
(1)利用公式 计算;列表表示。
(2)性质: 。
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
离散型随机变量及其分布列
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
二项分布与超几何分布
重伯努利试验特征:(1)同一个伯努力试验重复
做次;(2)各次试验结果相互独立。
X服从二项分布
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
二项分布与超几何分布
二项分布与超几何分布的区别:
放回抽样满足二项分布;不放回抽样满足超几何分布;
X服从超几何分布
抽样总数, 满足条件样本数, 抽取总数(或试验总数), 试验随机变量。
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
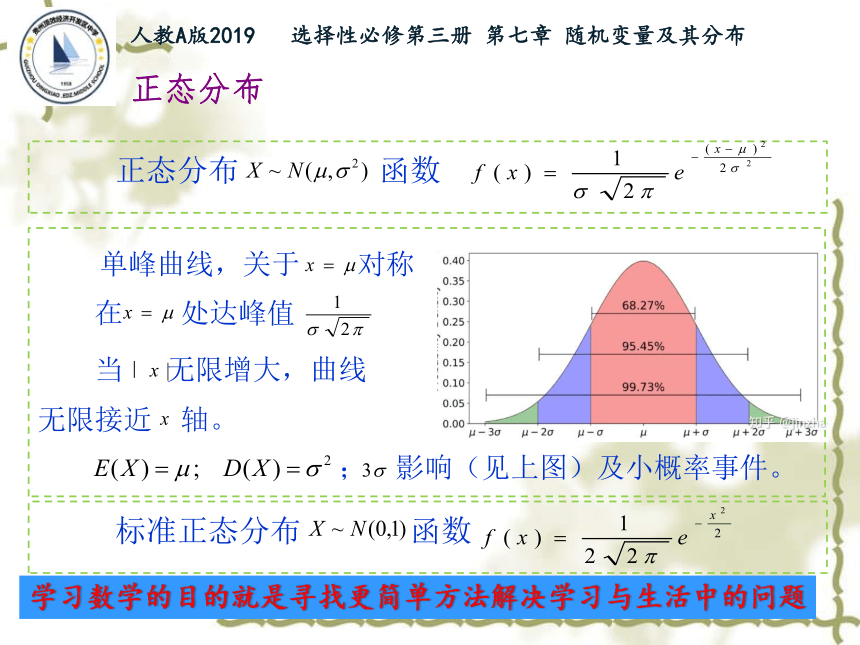
正态分布
正态分布 函数
标准正态分布 函数
单峰曲线,关于 对称
在 处达峰值
当 无限增大,曲线
无限接近 轴。
; 影响(见上图)及小概率事件。
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例1在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解:设“第1次抽到理科题”为事件A,“第2次抽到理科题”为事件B,则“第1次和第2次都抽到理科题”为事件AB.
(1)从5道题中不放回地依次抽取2道题包含的样本点数为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 条件概率的求解策略
其中(2)常用于古典概型的概率计算问题.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
变式训练1抛掷5枚硬币,在已知至少出现了2枚正面朝上的情况下,求正面朝上数恰好是3枚的概率.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例2某公司招聘员工,先由两位专家面试,若这两位专家都同意通过,则通过初审并予以录用;若这两位专家都未同意通过,则未通过初审并不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率均为 ,获得复审专家通过的概率为 ,各专家评审的结果相互独立.
(1)求某应聘人员被录用的概率.
(2)若4人应聘,设X为被录用的人数,试求随机变量X的分布列.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
故X的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 解决二项分布问题的两个关注点
(1)对于公式P(X=k)= pk(1-p)n-k(k=0,1,2,…,n)必须在随机变量服从二项分布时才能应用,否则不能应用.
(2)判断一个随机变量是否服从二项分布,关键有两点:一是对立性,即一次试验中,事件发生与否两者必有其一;二是重复性,即试验是独立重复地进行了n次.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
变式训练2一个暗箱里放着6个黑球、4个白球.
(1)依次不放回地取出3个球,若第1次取出的是白球,求第3次取到黑球的概率.
(2)有放回地依次取出3个球,若第1次取出的是白球,求第3次取到黑球的概率.
(3)有放回地依次取出3个球,求取到白球个数ξ的分布列和均值.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
解:(1)设事件A为“第1次取出的是白球”,事件B为“第3次取出的是黑球”,
(2)因为有放回地依次取出3个球,每次取出之前暗箱的情况没有变化,所以每次取球互不影响,
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例3在一次购物抽奖活动中,假设10张奖券中有一等奖奖券1张,可获价值50元的奖品,有二等奖奖券3张,每张可获价值10元的奖品,其余6张没有奖品.
(1)顾客甲从10张奖券中任意抽取1张,求中奖次数X的分布列;
(2)顾客乙从10张奖券中任意抽取2张,
①求顾客乙抽到中奖奖券数ξ的分布列;
②设顾客乙获得的奖品总价值为Y元,求Y的分布列.
故X的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
故ξ的分布列为
故Y的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 解决超几何分布问题的两个关键点
(1)超几何分布是概率分布的一种形式,一定要注意公式中字母的范围及其意义,解决问题时可以直接利用公式求解,但不能机械地记忆.
(2)在超几何分布中,只要知道M,N,n,就可以利用公式求出随机变量X取不同k值的概率P(X=k),从而求出X的分布列.
变式训练3老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格.某同学只能背诵其中的6篇,试求:
(1)抽到他能背诵的课文的数量X的分布列;
(2)他能及格的概率.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
故X的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例4一次同时投掷两枚相同的正方体骰子(骰子质地均匀,且各面分别刻有1,2,2,3,3,3六个数字).
(1)设随机变量η表示一次掷得的点数和,求η的分布列.
(2)若连续投掷10次,设随机变量ξ表示一次掷得的点数和大于5的次数,求E(ξ),D(ξ).
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 求离散型随机变量的均值与方差的步骤
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
变式训练4为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(1)设事件A为“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”,求事件A发生的概率;
(2)设X为选出的4人中种子选手的人数,求随机变量X的分布列和均值.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
故随机变量X的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例5设X~N(10,1).
(1)证明:P(1(2)设P(X≤2)=a,求P(10(1)证明:因为X~N(10,1),所以正态曲线f(x)关于直线x=10对称,而区间(1,2)和(18,19)关于直线x=10对称,
故P(1学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 正态分布的概率求法
(1)利用“3σ”原则,记住正态总体在三个区间内取值的概率.
(2)利用数形结合.由于正态分布密度曲线具有对称性,因此常结合图象,利用对称性,解决某一区间内的概率.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
解析:由题意,可知μ=60.5,σ=2,故P(58.5P(μ-σ答案:D
变式训练5为了解某地区高三男生的身体发育状况,抽查了该地区1 000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于58.5 kg,小于或等于62.5 kg属于正常情况,则这1 000名男生中属于正常
情况的人数约是( )
A.997 B.954
C.819 D.683
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
1.(2014·全国高考真题(理))某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 ( )
A.0.8 B.0.75 C.0.6 D.0.45
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
要点突破
1.在求n次独立重复试验中事件恰好发生k次的概率时,首先要确定好n和k的值,再准确利用公式求概率.
2.根据独立重复试验求二项分布的有关问题时,关键是理清事件与事件之间的关系,确定二项分布的试验次数n和变量的概率,求得概率.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
要点突破
超几何分布问题的两个关键点
(1)超几何分布是概率分布的一种形式,一定要注意公式中字母的范围及其意义,解决问题时可以直接利用公式求解,但不能机械地记忆.
(2)在超几何分布中,只要知道M,N,n,就可以利用公式求出随机变量X取不同k值的概率P(X=k),从而求出X的分布列.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
要点突破
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
章末复习与小结
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
学习内容
01 知识归纳
02 应用提升
03 对接高考
04 要点突破
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
学习目标
1.厘清随机变量及其分布;
2.筑牢章节知识体系;
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
本章知识结构
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
条件概率是学习相互独立事件的前提和基础,计算条件概率时必须弄清要求的条件概率是在什么条件下发生的概率。
条件概率与全概率
解决条件概率问题,主要有以下几种方法:
(1)利用公式 计算;
(2)针对古典概型,可通过缩减基本事件总数求解。
(3)注意公式 的应用。
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
条件概率与全概率
解决全概率问题,主要有以下几种方法:
(1)结合古典概型与条件概率,厘清所求概率的含义。
(2)全概率公式
(3)注意公式的意义
(贝叶斯公式)
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
离散型随机变量及其分布列
X的概率分布列,简称分布列:
(1)利用公式 计算;列表表示。
(2)性质: 。
厘清所解决问题含义,准确确定变量取值
X服从两点分布,或0-1分布:
(1)利用公式 计算;列表表示。
(2)性质: 。
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
离散型随机变量及其分布列
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
二项分布与超几何分布
重伯努利试验特征:(1)同一个伯努力试验重复
做次;(2)各次试验结果相互独立。
X服从二项分布
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
二项分布与超几何分布
二项分布与超几何分布的区别:
放回抽样满足二项分布;不放回抽样满足超几何分布;
X服从超几何分布
抽样总数, 满足条件样本数, 抽取总数(或试验总数), 试验随机变量。
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
正态分布
正态分布 函数
标准正态分布 函数
单峰曲线,关于 对称
在 处达峰值
当 无限增大,曲线
无限接近 轴。
; 影响(见上图)及小概率事件。
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例1在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解:设“第1次抽到理科题”为事件A,“第2次抽到理科题”为事件B,则“第1次和第2次都抽到理科题”为事件AB.
(1)从5道题中不放回地依次抽取2道题包含的样本点数为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 条件概率的求解策略
其中(2)常用于古典概型的概率计算问题.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
变式训练1抛掷5枚硬币,在已知至少出现了2枚正面朝上的情况下,求正面朝上数恰好是3枚的概率.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例2某公司招聘员工,先由两位专家面试,若这两位专家都同意通过,则通过初审并予以录用;若这两位专家都未同意通过,则未通过初审并不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率均为 ,获得复审专家通过的概率为 ,各专家评审的结果相互独立.
(1)求某应聘人员被录用的概率.
(2)若4人应聘,设X为被录用的人数,试求随机变量X的分布列.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
故X的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 解决二项分布问题的两个关注点
(1)对于公式P(X=k)= pk(1-p)n-k(k=0,1,2,…,n)必须在随机变量服从二项分布时才能应用,否则不能应用.
(2)判断一个随机变量是否服从二项分布,关键有两点:一是对立性,即一次试验中,事件发生与否两者必有其一;二是重复性,即试验是独立重复地进行了n次.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
变式训练2一个暗箱里放着6个黑球、4个白球.
(1)依次不放回地取出3个球,若第1次取出的是白球,求第3次取到黑球的概率.
(2)有放回地依次取出3个球,若第1次取出的是白球,求第3次取到黑球的概率.
(3)有放回地依次取出3个球,求取到白球个数ξ的分布列和均值.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
解:(1)设事件A为“第1次取出的是白球”,事件B为“第3次取出的是黑球”,
(2)因为有放回地依次取出3个球,每次取出之前暗箱的情况没有变化,所以每次取球互不影响,
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例3在一次购物抽奖活动中,假设10张奖券中有一等奖奖券1张,可获价值50元的奖品,有二等奖奖券3张,每张可获价值10元的奖品,其余6张没有奖品.
(1)顾客甲从10张奖券中任意抽取1张,求中奖次数X的分布列;
(2)顾客乙从10张奖券中任意抽取2张,
①求顾客乙抽到中奖奖券数ξ的分布列;
②设顾客乙获得的奖品总价值为Y元,求Y的分布列.
故X的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
故ξ的分布列为
故Y的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 解决超几何分布问题的两个关键点
(1)超几何分布是概率分布的一种形式,一定要注意公式中字母的范围及其意义,解决问题时可以直接利用公式求解,但不能机械地记忆.
(2)在超几何分布中,只要知道M,N,n,就可以利用公式求出随机变量X取不同k值的概率P(X=k),从而求出X的分布列.
变式训练3老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格.某同学只能背诵其中的6篇,试求:
(1)抽到他能背诵的课文的数量X的分布列;
(2)他能及格的概率.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
故X的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例4一次同时投掷两枚相同的正方体骰子(骰子质地均匀,且各面分别刻有1,2,2,3,3,3六个数字).
(1)设随机变量η表示一次掷得的点数和,求η的分布列.
(2)若连续投掷10次,设随机变量ξ表示一次掷得的点数和大于5的次数,求E(ξ),D(ξ).
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 求离散型随机变量的均值与方差的步骤
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
变式训练4为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(1)设事件A为“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”,求事件A发生的概率;
(2)设X为选出的4人中种子选手的人数,求随机变量X的分布列和均值.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
故随机变量X的分布列为
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
例5设X~N(10,1).
(1)证明:P(1
故P(1
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
方法技巧 正态分布的概率求法
(1)利用“3σ”原则,记住正态总体在三个区间内取值的概率.
(2)利用数形结合.由于正态分布密度曲线具有对称性,因此常结合图象,利用对称性,解决某一区间内的概率.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
应用提升
解析:由题意,可知μ=60.5,σ=2,故P(58.5
变式训练5为了解某地区高三男生的身体发育状况,抽查了该地区1 000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于58.5 kg,小于或等于62.5 kg属于正常情况,则这1 000名男生中属于正常
情况的人数约是( )
A.997 B.954
C.819 D.683
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
1.(2014·全国高考真题(理))某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 ( )
A.0.8 B.0.75 C.0.6 D.0.45
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
链接高考
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
要点突破
1.在求n次独立重复试验中事件恰好发生k次的概率时,首先要确定好n和k的值,再准确利用公式求概率.
2.根据独立重复试验求二项分布的有关问题时,关键是理清事件与事件之间的关系,确定二项分布的试验次数n和变量的概率,求得概率.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
要点突破
超几何分布问题的两个关键点
(1)超几何分布是概率分布的一种形式,一定要注意公式中字母的范围及其意义,解决问题时可以直接利用公式求解,但不能机械地记忆.
(2)在超几何分布中,只要知道M,N,n,就可以利用公式求出随机变量X取不同k值的概率P(X=k),从而求出X的分布列.
学习数学的目的就是寻找更简单方法解决学习与生活中的问题
人教A版2019 选择性必修第三册 第七章 随机变量及其分布
要点突破
