《一元一次方程》全章复习与巩固(基础)知识讲解
文档属性
| 名称 | 《一元一次方程》全章复习与巩固(基础)知识讲解 | 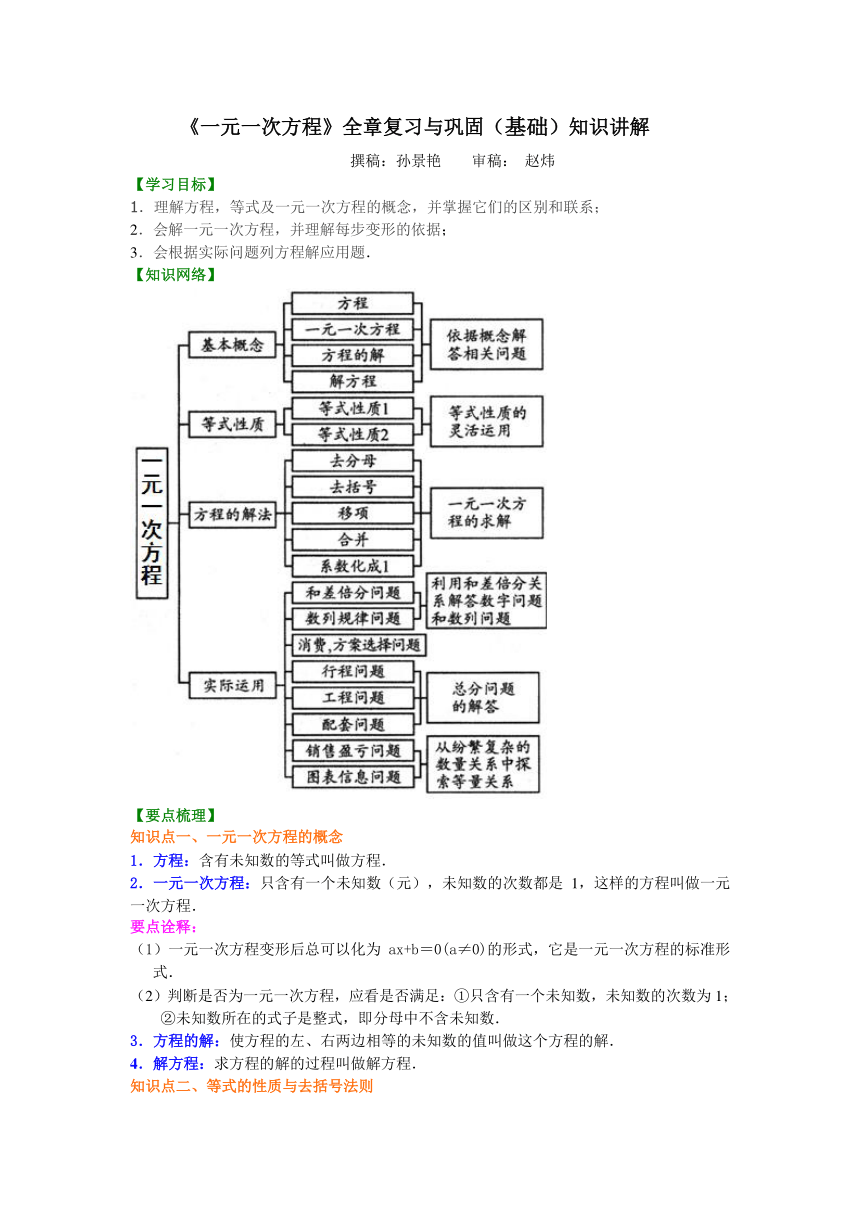 | |
| 格式 | zip | ||
| 文件大小 | 217.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-27 13:47:53 | ||
图片预览


文档简介
《一元一次方程》全章复习与巩固(基础)知识讲解
撰稿:孙景艳 审稿: 赵炜
【学习目标】
1.理解方程,等式及一元一次方程的概念,并掌握它们的区别和联系;
2.会解一元一次方程,并理解每步变形的依据;
3.会根据实际问题列方程解应用题.
【知识网络】
( http: / / www.21cnjy.com )
【要点梳理】
知识点一、一元一次方程的概念
1.方程:含有未知数的等式叫做方程.
2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程.
要点诠释:
(1)一元一次方程变形后总可以化为ax+b=0(a≠0)的形式,它是一元一次方程的标准形式.
(2)判断是否为一元一次方程,应看是否满足:①只含有一个未知数,未知数的次数为1;
②未知数所在的式子是整式,即分母中不含未知数.
3.方程的解:使方程的左、右两边相等的未知数的值叫做这个方程的解.
4.解方程:求方程的解的过程叫做解方程.
知识点二、等式的性质与去括号法则
1.等式的性质:
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
2.合并法则:合并时,把系数相加(减)作为结果的系数,字母的指数不变.
3.去括号法则:
(1)括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
(2)括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反.
知识点三、一元一次方程的解法
解一元一次方程的一般步骤:
(1)去分母:在方程两边同乘以各分母的最小公倍数.
(2)去括号:依据乘法分配律和去括号法则,先去小括号,再去中括号,最后去大括号.
(3)移项:把含有未知数的项移到方程一边,常数项移到方程另一边.
(4)合并:逆用乘法分配律,分别合并含有未知数的项及常数项,把方程化为ax=b(a≠0)的形式.
(5)系数化为1:方程两边同除以未知数的系数得到方程的解(a≠0).
(6)检验:把方程的解代入原方程,若方程左右两边的值相等,则是方程的解;若方程左右两边的值不相等,则不是方程的解.
知识点四、用一元一次方程解决实际问题的常见类型
1.行程问题:路程=速度×时间
2.和差倍分问题:增长量=原有量×增长率
3.利润问题:商品利润=商品售价-商品进价
4.工程问题:工作量=工作效率×工作时间,各部分劳动量之和=总量
5.银行存贷款问题:本息和=本金+利息,利息=本金×利率×期数
6.数字问题:多位数的表示方法:例如:.
【典型例题】
类型一、一元一次方程的概念
1.下列方程中,哪些是一元一次方程 哪些不是
(1); (2)2x+y=5; (3)x2-5x+6=0; (4); (5).
【思路点拨】若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.
【答案】 (1)、(5)是一元一次方程.因为它们或等价变形后是只含有一个未知数、并且未知数的次数是1的方程;
(2)、(3)、(4)都不是一元一次方 ( http: / / www.21cnjy.com )程,因为(2)中含有两个未知数;(3)中未知数的最高次数是2;(4)中分母含有未知数,它不是整式方程.
【解析】判断一个方程是不是一元一次方程,有时需要对方程进行等价变形后再判断.例如:
,可化为:,所以 是一元一次方程.
【总结升华】凡是分母中含有未知数的方程一定不是一元一次方程.
举一反三:
【高清课堂:一元一次方程复习 393349 等式和方程 例(1)】
【变式】下列说法中正确的是( ).
A.2a-a=a不是等式 B.x2-2x-3是方程 C.方程是等式 D.等式是方程
【答案】C
2. 若方程3(x-1)+8=2x+3与方程的解相同,求k的值.
【答案与解析】
解:解方程3(x-1)+8=2x+3,得x=-2.
将x=-2代入方程中,得.
解这个关于k的方程,得.
所以,k的值是.
【总结升华】由于两个方程的解相同,所以可以将其中一个方程的解代入另一个方程中,从而求得问题的答案.
举一反三:
【变式】若关于x的方程2(x-1)-a=0的解是x=3,则a的值是( ).
A.4 B.-4 C.5 D.-5
【答案】A.
类型二、一元一次方程的解法
3.解方程
【思路点拨】通过方程的同解原理(去分母,去 ( http: / / www.21cnjy.com )括号,合并同类项,系数化为1),一步一步将一个复杂的方程转化成与它同解的最简的方程,从而达到求解的目的.
【答案与解析】
解:去分母,得3(y+2)-2(3-5y)=12
去括号,得3y+6-6+10y=12
合并同类项,得13y=12
未知数的系数化为1,得
【总结升华】转化思想是初中数学中一种常见的 ( http: / / www.21cnjy.com )思想方法,它能将复杂的问题转化为简单的问题,将生疏的问题转化为熟悉的问题,将未知转化为已知.事实上解一元一次方程就是利用方程的同解原理,将复杂的方程转化为简单的方程直至求出它的解.
4.解方程:
【思路点拨】本题按常规方法求解,比较繁锁,如能根据题目的特点,巧用“整体思维”,就能算得又快又对,起到事半功倍的效果.
【答案与解析】
解:
x=-6
【总结升华】直接去括号太繁琐,若将(x+1)及(x-1)看作一个整体,并移项合并同类项,解答十分巧妙,可免去去分母的步骤及简化去括号的过程.
举一反三:
【变式】解方程:278(x-4)-463(8-2x)-888(7x-28)=0
【答案】
解:原方程可化为278(x-4)+463×2(x-4)-888×7(x-4)=0
(x-4)(278+463×2-888×7)=0
x-4=0
x=4
类型三、一元一次方程的应用
5. (南京)甲车从A地出发以60 km/h的速度沿公路匀速行驶,0.5 h后,乙车也从A地出发,以80 km/h的速度沿该公路与甲车同向匀速行驶,求乙车出发后几小时追上甲车.
【答案与解析】
解:设乙车出发后x小时追上甲车,依题意得60×0.5+60x=80x,解得x=1.5.
答:乙车出发后1.5小时追上甲车.
【总结升华】此题的等量关系为:甲前0.5 h的行程+甲后来的行程=乙的行程.
6. (南昌)剃须刀由刀片和刀架组成.某时期,甲、乙两厂家分别生产老式剃须刀(刀片不可更换)和新式剃须刀(刀片可更换).有关销售策略与售价等信息如下表所示:
( http: / / www.21cnjy.com )
某段时间内,甲厂家 ( http: / / www.21cnjy.com )销售了8400把剃须刀,乙厂家销售的刀片数量是刀架数量的50倍,乙厂家获得的利润是甲厂家的两倍,问这段时间内乙厂家销售了多少把刀架 多少片刀片
【答案与解析】
解:设这段时间内乙厂家销售了x把刀架.
依题意,得(0.55-0.05)·50x+(1-5)x=2×(2.5—2)×8400,
解得x=400.
销售出的刀片数:50×400=20000(片).
答:这段时间内乙厂家销售了400把刀架,20000片刀片.
【总结升华】本题的相等关系为:甲厂家利润×2=乙厂家利润.
举一反三:
【高清课堂:一元一次方程复习 393349 一元一次方程的解法和应用例6】
【变式】某文具店为促销X型计算器,优惠 ( http: / / www.21cnjy.com )条件是一次购买不超过10个,每个38元,超过10个,超过部分每个让利2元(即每个36元),问李老师用812元共买了多少个?
【答案】
解:设李老师用812元共买了个,依题意可得:
解得:
答:李老师用812元共买了22个.
撰稿:孙景艳 审稿: 赵炜
【学习目标】
1.理解方程,等式及一元一次方程的概念,并掌握它们的区别和联系;
2.会解一元一次方程,并理解每步变形的依据;
3.会根据实际问题列方程解应用题.
【知识网络】
( http: / / www.21cnjy.com )
【要点梳理】
知识点一、一元一次方程的概念
1.方程:含有未知数的等式叫做方程.
2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程.
要点诠释:
(1)一元一次方程变形后总可以化为ax+b=0(a≠0)的形式,它是一元一次方程的标准形式.
(2)判断是否为一元一次方程,应看是否满足:①只含有一个未知数,未知数的次数为1;
②未知数所在的式子是整式,即分母中不含未知数.
3.方程的解:使方程的左、右两边相等的未知数的值叫做这个方程的解.
4.解方程:求方程的解的过程叫做解方程.
知识点二、等式的性质与去括号法则
1.等式的性质:
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
2.合并法则:合并时,把系数相加(减)作为结果的系数,字母的指数不变.
3.去括号法则:
(1)括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
(2)括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反.
知识点三、一元一次方程的解法
解一元一次方程的一般步骤:
(1)去分母:在方程两边同乘以各分母的最小公倍数.
(2)去括号:依据乘法分配律和去括号法则,先去小括号,再去中括号,最后去大括号.
(3)移项:把含有未知数的项移到方程一边,常数项移到方程另一边.
(4)合并:逆用乘法分配律,分别合并含有未知数的项及常数项,把方程化为ax=b(a≠0)的形式.
(5)系数化为1:方程两边同除以未知数的系数得到方程的解(a≠0).
(6)检验:把方程的解代入原方程,若方程左右两边的值相等,则是方程的解;若方程左右两边的值不相等,则不是方程的解.
知识点四、用一元一次方程解决实际问题的常见类型
1.行程问题:路程=速度×时间
2.和差倍分问题:增长量=原有量×增长率
3.利润问题:商品利润=商品售价-商品进价
4.工程问题:工作量=工作效率×工作时间,各部分劳动量之和=总量
5.银行存贷款问题:本息和=本金+利息,利息=本金×利率×期数
6.数字问题:多位数的表示方法:例如:.
【典型例题】
类型一、一元一次方程的概念
1.下列方程中,哪些是一元一次方程 哪些不是
(1); (2)2x+y=5; (3)x2-5x+6=0; (4); (5).
【思路点拨】若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.
【答案】 (1)、(5)是一元一次方程.因为它们或等价变形后是只含有一个未知数、并且未知数的次数是1的方程;
(2)、(3)、(4)都不是一元一次方 ( http: / / www.21cnjy.com )程,因为(2)中含有两个未知数;(3)中未知数的最高次数是2;(4)中分母含有未知数,它不是整式方程.
【解析】判断一个方程是不是一元一次方程,有时需要对方程进行等价变形后再判断.例如:
,可化为:,所以 是一元一次方程.
【总结升华】凡是分母中含有未知数的方程一定不是一元一次方程.
举一反三:
【高清课堂:一元一次方程复习 393349 等式和方程 例(1)】
【变式】下列说法中正确的是( ).
A.2a-a=a不是等式 B.x2-2x-3是方程 C.方程是等式 D.等式是方程
【答案】C
2. 若方程3(x-1)+8=2x+3与方程的解相同,求k的值.
【答案与解析】
解:解方程3(x-1)+8=2x+3,得x=-2.
将x=-2代入方程中,得.
解这个关于k的方程,得.
所以,k的值是.
【总结升华】由于两个方程的解相同,所以可以将其中一个方程的解代入另一个方程中,从而求得问题的答案.
举一反三:
【变式】若关于x的方程2(x-1)-a=0的解是x=3,则a的值是( ).
A.4 B.-4 C.5 D.-5
【答案】A.
类型二、一元一次方程的解法
3.解方程
【思路点拨】通过方程的同解原理(去分母,去 ( http: / / www.21cnjy.com )括号,合并同类项,系数化为1),一步一步将一个复杂的方程转化成与它同解的最简的方程,从而达到求解的目的.
【答案与解析】
解:去分母,得3(y+2)-2(3-5y)=12
去括号,得3y+6-6+10y=12
合并同类项,得13y=12
未知数的系数化为1,得
【总结升华】转化思想是初中数学中一种常见的 ( http: / / www.21cnjy.com )思想方法,它能将复杂的问题转化为简单的问题,将生疏的问题转化为熟悉的问题,将未知转化为已知.事实上解一元一次方程就是利用方程的同解原理,将复杂的方程转化为简单的方程直至求出它的解.
4.解方程:
【思路点拨】本题按常规方法求解,比较繁锁,如能根据题目的特点,巧用“整体思维”,就能算得又快又对,起到事半功倍的效果.
【答案与解析】
解:
x=-6
【总结升华】直接去括号太繁琐,若将(x+1)及(x-1)看作一个整体,并移项合并同类项,解答十分巧妙,可免去去分母的步骤及简化去括号的过程.
举一反三:
【变式】解方程:278(x-4)-463(8-2x)-888(7x-28)=0
【答案】
解:原方程可化为278(x-4)+463×2(x-4)-888×7(x-4)=0
(x-4)(278+463×2-888×7)=0
x-4=0
x=4
类型三、一元一次方程的应用
5. (南京)甲车从A地出发以60 km/h的速度沿公路匀速行驶,0.5 h后,乙车也从A地出发,以80 km/h的速度沿该公路与甲车同向匀速行驶,求乙车出发后几小时追上甲车.
【答案与解析】
解:设乙车出发后x小时追上甲车,依题意得60×0.5+60x=80x,解得x=1.5.
答:乙车出发后1.5小时追上甲车.
【总结升华】此题的等量关系为:甲前0.5 h的行程+甲后来的行程=乙的行程.
6. (南昌)剃须刀由刀片和刀架组成.某时期,甲、乙两厂家分别生产老式剃须刀(刀片不可更换)和新式剃须刀(刀片可更换).有关销售策略与售价等信息如下表所示:
( http: / / www.21cnjy.com )
某段时间内,甲厂家 ( http: / / www.21cnjy.com )销售了8400把剃须刀,乙厂家销售的刀片数量是刀架数量的50倍,乙厂家获得的利润是甲厂家的两倍,问这段时间内乙厂家销售了多少把刀架 多少片刀片
【答案与解析】
解:设这段时间内乙厂家销售了x把刀架.
依题意,得(0.55-0.05)·50x+(1-5)x=2×(2.5—2)×8400,
解得x=400.
销售出的刀片数:50×400=20000(片).
答:这段时间内乙厂家销售了400把刀架,20000片刀片.
【总结升华】本题的相等关系为:甲厂家利润×2=乙厂家利润.
举一反三:
【高清课堂:一元一次方程复习 393349 一元一次方程的解法和应用例6】
【变式】某文具店为促销X型计算器,优惠 ( http: / / www.21cnjy.com )条件是一次购买不超过10个,每个38元,超过10个,超过部分每个让利2元(即每个36元),问李老师用812元共买了多少个?
【答案】
解:设李老师用812元共买了个,依题意可得:
解得:
答:李老师用812元共买了22个.
