第三章 整式及其加减单元检测题(含解析)
文档属性
| 名称 | 第三章 整式及其加减单元检测题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 593.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 16:52:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2023-2024学年度七年级上册数学第三章整式及其加减单元综合检测题
一、单选题
1.式子中,单项式有( )
A.1个 B.2个 C.3个 D.4个
2.下列各式符合代数式书写规则的是( )
A.a×5 B.a7 C. D.
3.某品牌冰箱进价为每台m元,提高20%作为标价.元旦期间按标价的9折出售,则出售一台这种冰箱可获得利润( )
A.m元 B.m元 C.m元 D.m元
4.多项式与多项式的和不含二次项,则m为( )
A.2 B. C.4 D.
5.如图,用规格相同的小棒按照图案规律摆放,2022根小棒最多可以摆出多少个小正方形?( )
A.503 B.124 C.808 D.252
6.如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点……按照此规律,第一百幅图中圆点的个数是( )
A.297 B.301 C.303 D.400
7.如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
A.2a﹣3b B.4a﹣8b C.2a﹣4b D.4a﹣10b
8.观察下列各式及其展开式
……
请你猜想的展开式从左往右第三项的系数是( )
A.35 B.45 C.55 D.66
二、填空题
9.单项式的系数是 ________,次数是_______.
10.多项式﹣3x+7是关于x的四次三项式,则m的值是_____.
11.按规律排列的单项式:﹣x,x3,﹣x5,x7,﹣x9,…,那么第15个单项式是 _____.
12.设甲数为x,乙数比甲数的3倍少6,则乙数用代数式表示为______.
13.一个三位数的十位为m,个位数比十位数的3倍多2,百位数比个位数少3,则这个三位数可表示为________.
14.若关于a,b的多项式中不含项,则m=_____.
15.若,则_____;
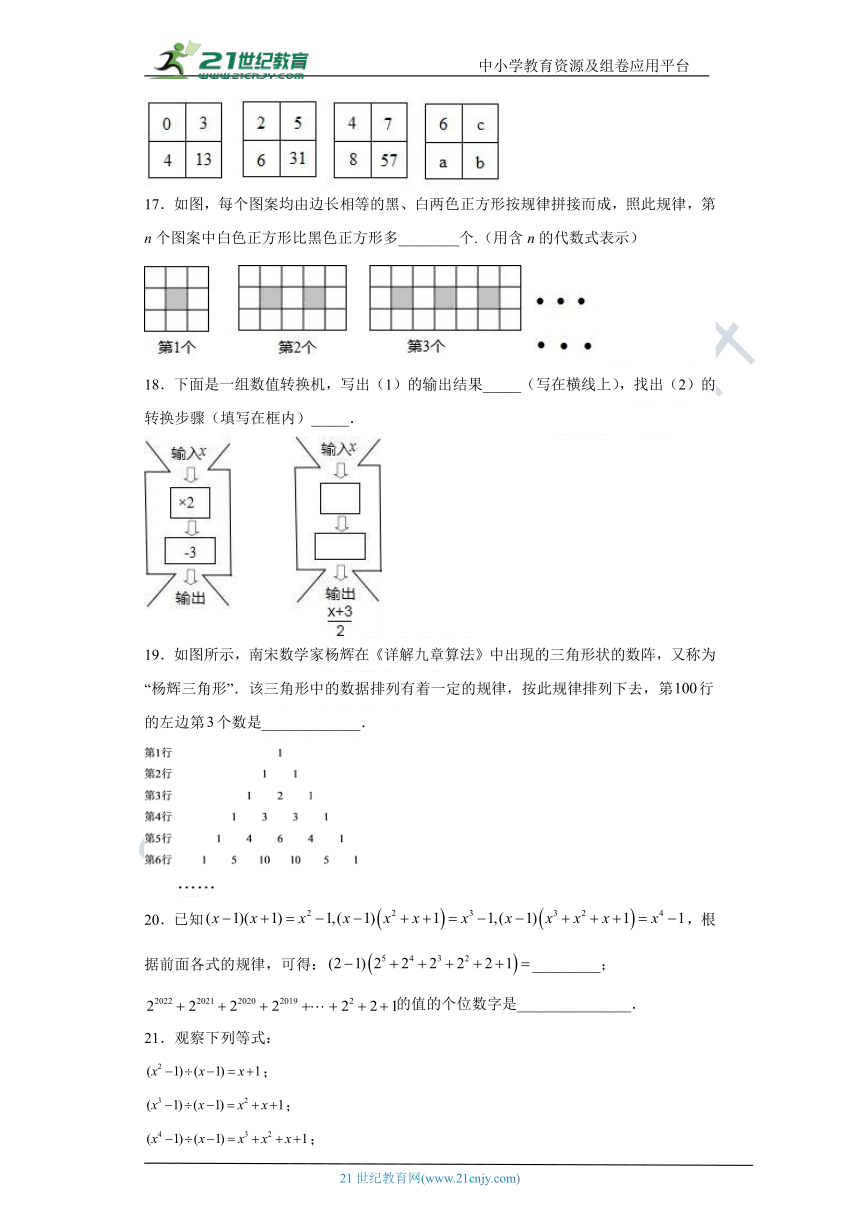
16.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a+b+c=____.
17.如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)
18.下面是一组数值转换机,写出(1)的输出结果_____(写在横线上),找出(2)的转换步骤(填写在框内)_____.
19.如图所示,南宋数学家杨辉在《详解九章算法》中出现的三角形状的数阵,又称为“杨辉三角形”.该三角形中的数据排列有着一定的规律,按此规律排列下去,第行的左边第个数是_____________.
20.已知,根据前面各式的规律,可得:_________;的值的个位数字是_______________.
21.观察下列等式:
;
;
;
;
;
根据以上等式总结规律并计算,则______.
三、解答题
22.计算
(1);
(2);
(3);
(4);
(5).
23.计算:
(1);
(2);
(3);
(4).
24.已知,,求:
(1)A+B;
(2)2A-B.
25.已知:,求的值.
26.化简:
(1)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b);
(2)5x2﹣[3x﹣2(2x﹣3)+7x2];
(3)先化简再求值:3a2b﹣[3a2b﹣(2abc﹣a2c)﹣4a2c]﹣abc.(若a=﹣2,b=﹣1,c=).
27.某同学做一道数学题:已知两个多项式A、B,计算,他误将“”看成“”,求得的结果是,已知,求的正确答案.
28.已知(m+3)x3y|m+1|是关于x,y的七次单项式,求m2﹣3m+1的值.
29.已知,a与b互为倒数,c与d互为相反数,求的值.
30.如图,若图中平面展开图折叠成正方体后,相对面上的两个数字互为相反数,求的值.
31.初一年级学生在名教师的带领下去公园秋游,公园的门票为每人元.现有两种优惠方案,甲方案:带队教师免费,学生按折收费;乙方案:师生都折收费.
若有名学生,用代数式表示两种优惠方案各需多少元?
当时,采用哪种方案优惠?
当时,采用哪种方案优惠?
32.如图,正方形和正方形的边长分别为a和6,点在一条直线上,点在一条直线上,将依次连接所围成的阴影部分的面积记为S阴影
(1)试用含a的代数式表示S阴影;
(2)当时,比较S阴影与面积的大小;当时,结论是否改变?为什么?
33.阅读下列材料:小明为了计算的值 ,采用以下方法:
设 ①
则 ②
②-①得
∴
(1)= ;
(2) = ;
(3)求的和( ,是正整数,请写出计算过程 ).
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据单项式定义逐个判断即可
【详解】解:题中的式子中单项式有、2x,共2个.
故选B.
【点睛】本题主要考查了单项式的定义,数字或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式.
2.D
【分析】根据代数式的书写要求判断各项.
【详解】解:A、数与字母相乘,数应该写在前边,乘号通常简写成“ ”或者省略不写,故此选项不符合题意;
B、数与字母相乘,数应该写在前边,故此选项不符合题意;
C、分数与字母相乘,带分数应该写成假分数的形式,故此选项不符合题意;
D、符合代数式的书写要求,故此选项符合题意.
故选:D.
【点睛】此题考查了代数式的书写,解题的关键是掌握代数式的书写要求.代数式的书写要求:(1)在代数式中出现的乘号,通常简写成“ ”或者省略不写;(2)数字与字母相乘时,数字要写在字母的前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写,带分数要写成假分数的形式.
3.D
【分析】先求出标价,再求出销售价,利用公式利润=售价-进价计算即可.
【详解】某品牌冰箱进价为每台m元,
提高20%作标价为:(1+20%)m元,
按标价的9折出售的售价为:1.2m×=1.08m元,
出售一台这种冰箱可获得利润=1.08m-m=0.08m元,
故答案为:D.
【点睛】本题考查销售利润问题,掌握标价,进价与利润率关系,标价折数与售价关系,售价进价与利润关系是解题关键.
4.C
【分析】由题意可以得到关于m的方程,解方程即可得到问题答案.
【详解】解:由题意可得:,
,
∵它们的和不含二次项
∴,
解之可得:,
故选:C.
【点睛】本题考查多项式的应用,熟练掌握多项式的相关概念是解题关键.
5.D
【分析】仔细观察发现,出现1个正六边形和1个小正方形时,需要小棒的根数是9根;出现2个正六边形和2个小正方形时,需要小棒的根数是17根;出现3个正六边形和3个小正方形时,需要小棒的根数是25根;……由此得出规律.
【详解】解:出现1个正六边形和1个小正方形时,需要小棒的根数是9根;
出现2个正六边形和2个小正方形时,需要小棒的根数是17根;
出现3个正六边形和3个小正方形时,需要小棒的根数是25根;
…,
则出现n个正六边形和n个小正方形时,需要小棒的根数是(8n+1)根;
(2022-1)÷8=252……5,
故选:D.
【点睛】本题主要考查图形的变化规律,根据图案的变化归纳出出现n个正六边形和n个小正方形时,需要小棒的根数是(8n+1)根是解题的关键.
6.B
【分析】首先根据前几个图形圆点的个数规律即可发现规律,从而得到第100个图摆放圆点的个数.
【详解】解:观察图形可知:第1幅图案需要4个圆点,即4+3×0,
第2幅图7个圆点,即4+3=4+3×1;
第3幅图10个圆点,即4+3+3=4+3×2;
第4幅图13个圆点,即4+3+3+3=4+3×3;
第n幅图中,圆点的个数为:4+3(n-1)=3n+1,
……,
第100幅图,圆中点的个数为:3×100+1=301.
故选:B.
【点睛】本题主要考查了图形的变化规律,解答的关键是由所给的图形总结出存在的规律.
7.B
【分析】剪下的两个小矩形的长为a b,宽为(a 3b),所以这两个小矩形拼成的新矩形的长为(a b),宽为(a 3b),然后计算这个新矩形的周长.
【详解】解:根据题意得:2(a﹣b+a﹣3b)=2(2a﹣4b)=4a﹣8b,
故选B.
【点睛】本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.解题的关键用a和b表示出剪下的两个小矩形的长与宽.
8.C
【分析】利用所给展开式探求各项系数的关系,特别是上面的展开式与下面的展开式中的各项系数的关系,可推出的展开式从左往右第三项的系数.
【详解】解:
∴依据规律可得到:
第三项的系数为1,
第三项的系数为,
第三项的系数为,
第三项的系数为:.
故选:C.
【点睛】此题考查了数字规律型,理解题意,找到系数的规律是解题的关键.
9.
【分析】直接根据单项式的系数与次数的定义得出答案,单项式中的数字因数叫做单项式的系数,一个单项式中所有字母的指数的和叫做单项式的次数.
【详解】解:单项式的系数和次数分别是:,.
故答案为:,6.
【点睛】本题考查了单项式的系数,单项式的次数,理解单项式的系数与次数是解题的关键.
10.5
【分析】根据多项式中次数最高的项的次数叫做多项式的次数进行分析即可.
【详解】解:∵多项式﹣3x+7是关于x的四次三项式,
∴m﹣1=4,
解得m=5,
故答案为:5.
【点睛】此题考查的是多项式的次数,掌握多项式的次数的定义是解决此题的关键.
11.
【分析】由题意可得第n个单项式是(﹣1)nx2n﹣1,当n=15时代入即可求解.
【详解】解:∵﹣x,x3,﹣x5,x7,﹣x9,…,
∴第n个单项式是(﹣1)nx2n﹣1,
∴第15个单项式是(﹣1)15x2×15﹣1
∴第15个单项式是﹣x29,
故答案为:﹣x29.
【点睛】本题考查数字的变化规律,根据所给的单项式的特点,探索出单项式的一般规律是解题的关键.
12.3x-6
【分析】根据题意列出代数式即可.
【详解】∵乙数比甲数的3倍少6,设甲数为x,
∴乙数是:3x-6.
故答案是:3x-6.
【点睛】考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系,列出代数式.
13.
【分析】根据题意先表示个位数为:再表示百位数为:从而可得答案.
【详解】解: 一个三位数的十位为m,个位数比十位数的3倍多2,百位数比个位数少3,
个位数为: 百位数为:
所以这个三位数为:
故答案为:
【点睛】本题考查的是列代数式,整式的加减运算,一个三位数的百位,十位,个位为分别为 则这个三位数表示为: 掌握列式的方法是解题的关键.
14.2
【分析】原式去括号合并得到最简结果,根据结果不含ab项,求出m的值即可.
【详解】原式,
由结果不含项,得到,
解得:.
故答案为:2.
【点睛】本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.
15.2029
【分析】先由,得,然后将变形为x[2(x2-2x)-3x+12]+2020,代入得x(-3x+6)+2020,再变形为-3(x2-2x)+2020,再代入则可求解.
【详解】解:∵,
∴,
∴
=x(2x2-4x-3x+12)+2020
=x[2(x2-2x)-3x+12]+2020
= x[2×(-3)-3x+12]+2020
=x(-3x+6)+2020
=-3(x2-2x)+2020
=-3×(-3)+2020
=9+2020
=2029
故答案为:2029.
【点睛】本题考查代数式求值,将代数式变形为已知式子形式是解题的关键.
16.110
【详解】试题分析:根据前三个正方形中的数字规律可知:C所处的位置上的数字是连续的奇数,所以c=9,而a所处的位置上的数字是连续的偶数,所以a=10,而b=ac+1=9×10+1=91,所以a+b+c=9+10+91=110.
考点:数字规律.
17.4n+3
【分析】利用给出的三个图形寻找规律,发现白色正方形个数=总的正方形个数-黑色正方形个数,而黑色正方形个数第1个为1,第二个为2,由此寻找规律,总个数只要找到边与黑色正方形个数之间关系即可,依此类推,寻找规律.
【详解】解:方法一:
第1个图形黑、白两色正方形共3×3个,其中黑色1个,白色3×3-1个,
第2个图形黑、白两色正方形共3×5个,其中黑色2个,白色3×5-2个,
第3个图形黑、白两色正方形共3×7个,其中黑色3个,白色3×7-3个,
依此类推,
第n个图形黑、白两色正方形共3×(2n+1)个,其中黑色n个,白色3×(2n+1)-n个,
即:白色正方形5n+3个,黑色正方形n个,
故第n个图案中白色正方形比黑色正方形多4n+3个,
方法二
第1个图形白色正方形共8个,黑色1个,白色比黑色多7个,
第2个图形比第1个图形白色比黑色又多了4个,即白色比黑色多(7+4)个,
第3个图形比第2个图形白色比黑色又多了4个,即白色比黑色多(7+4×2)个,
类推,第n个图案中白色正方形比黑色正方形多[7+4(n-1)]个,即(4n+3)个,
故第n个图案中白色正方形比黑色正方形多4n+3个.
【点睛】本题考查了几何图形的变化规律,是探索型问题,图中的变化规律是解题的关键.
18. 2x-3 +3;2
【分析】根据图(1)可得:2x﹣3;图(2)中所表现出来的规律是x先加3,然后再让x加3的和除以2,即(x+3)÷2=.
【详解】(1)先算乘法,再减3,为:2x﹣3;
(2)先算加法,再除以2.先填“+3”,接下来填“÷2”.
故答案为(1)2x-3;(2)+3;2.
【点睛】要学会读图,能从图中找到规律,例如,(1)中所揭示的规律为:2x﹣3;(2)中可由结果判断出是x先加2,然后再让x加3的和除以2,此题主要考查阅读思考能力的灵活性.
19.
【分析】观察前几行左边第个数的排列规律,进而推出第100行的左边第个数.
【详解】解:从第3行开始:
第3行:左边第个数是1==;
第4行:左边第个数是3==;
第5行:左边第个数是6==;
第6行:左边第个数是10==;
……
第100行:左边第个数是==4851.
故答案为:4851.
【点睛】本题的关键是找出从第3行开始,每行的左边第3个数的排列规律:1,3,6,10,15…,进而得出第n行左边第个数是,由此得解.
20. ; 7
【分析】仿照阅读材料中的等式写出的结果即可;利用得出的规律化简,计算即可求出值.
【详解】解:由题意可得:;
由以上过程可知:,
∴,
∵,个位数字为2,,个位数字为4,,个位数字为8,,个位数字为6;
,个位数字为2,,个位数字为4,,个位数字为8,,个位数字为6;
…;
∴的各位数字与的各位数字相同,都是8,
∴的值的个位数字是8-1=7.
故答案为:; 7.
【点睛】本题考查规律问题等知识,解题的关键是学会或转化的思想思考问题,学会从特殊到一般的探究规律的方法.
21.255
【分析】根据所给出的等式找到规律,再利用式子的规律进行逆用即可求解.
【详解】解:由给出等式可知,,
∴
故答案为:255.
【点睛】本题考查数字的变化规律,能够根据题中所给式子探索出式子的规律是解题的关键.
22.(1)2ab;
(2);
(3);
(4);
(5)
【分析】原式各项去括号合并即可得到结果.
(1)=2ab;
(2)==;
(3)==;
(4)==;
(5)==.
【点睛】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.
23.(1);(2);(3);(4).
【分析】(1)先去括号,然后再合并同类项即可;
(2)先去括号,然后再合并同类项即可;
(3)先去括号,然后再合并同类项即可;
(4)先去括号,然后再合并同类项即可.
【详解】解:(1)
=
=
=;
(2)
=
=
=;
(3)
=
=
=;
(4)
=
=
=.
【点睛】本题主要考查了整式的加减运算,掌握去括号法则和合并同类项法则成为解答本题的关键.
24.(1)-2x+3
(2)
【分析】(1)根据整式加法的运算法则计算即可;
(2)根据整式减法的运算法则计算即可;
【详解】(1)
;
(2)
【点睛】本题考查整式的加法和减法.掌握整式的加法和减法的运算法则是解题关键.
25.;
【分析】先根据绝对值和平方的非负性求出x,y,再根据整式的混和运算法则化成最简,然后代入数值计算即可.
【详解】解:∵,
,
解得:,,
∴原式
.
当,时,
原式
.
【点睛】本题主要考查了整式的化简求值,根据非负性求出x,y的值是解题的关键.
26.(1)
(2)
(3)abc+3a2c,7
【分析】(1)先去括号,然后合并同类项,即可得到答案;
(2)先去括号,然后合并同类项,即可得到答案;
(3)先去括号,然后合并同类项进行化简,再把a=﹣2,b=﹣1,c=代入计算,即可求出答案.
【详解】(1)解:原式=
=;
(2)解:原式=
=
=;
(3)解:3a2b﹣[3a2b﹣(2abc﹣a2c)﹣4a2c]﹣abc
=3a2b﹣3a2b+(2abc﹣a2c)+4a2c﹣abc
=3a2b﹣3a2b+2abc﹣a2c+4a2c﹣abc
=abc+3a2c,
当a=﹣2,b=﹣1,时,
原式=﹣2×(﹣1)×+3×(﹣2)2×=1+6=7;
【点睛】本题考查了整式的加减运算,整式的化简求值,解题的关键是熟练掌握运算法则,正确的进行化简.
27.
【分析】根据题意得,求出A的值,代入后求出即可.
【详解】解:∵
,
∴
.
【点睛】本题考查了整式的加减的应用,关键是求出A的值.
28.1或41
【分析】直接利用单项式的系数和次数确定方法分析得出答案.
【详解】解:∵(m+3)x3y|m+1|是关于x,y的七次单项式,
∴3+|m+1|=7且m+3≠0,
解得:m=3,或m=﹣5,
∴m2﹣3m+1=9﹣9+1=1,
或m2﹣3m+1=25+15+1=41.
故m2﹣3m+1的值是1或41.
【点睛】此题主要考查了单项式,正确把握单项式的系数和次数确定方法是解题关键.
29.-2
【分析】根据绝对值的性质、平方的性质可知,,再由相反数的性质,倒数的性质得出ab、c+d的值,再代入代数式计算可得.
【详解】解:,
,
,
因为与互为倒数,所以
因为与互为相反数,所以
原式
=-2.
【点睛】本题主要考查非负数的性质,互为倒数,互为相反数,代数式求值,含乘方的有理数混合运算,解题的关键是熟练掌握混合运算顺序和运算法则.
30.
【分析】根据正方体的展开图,判断出相对的面,利用相对面上的两个数字互为相反数,求出x、y、z,进而计算出x-y+z的值即可.
【详解】解:由题意得与,与,与分别是相对面上的两个数,
所以,,,
所以.
【点睛】考查正方体的展开与折叠,正方体的展开图中“相间、Z端是对面”判断对面.
31.(1) 甲16m, 乙:;(2) 甲方案优惠,理由见解析;(3) 乙方案优惠,理由见解析
【分析】 根据题意确定两种优惠方案所需的钱数;
把代入计算,比较即可;
把代入计算,比较即可得到答案.
【详解】解:甲方案需要的钱数为:,
乙方案需要的钱数为:;
当时,
乙方案:(元),
甲方案:(元),
∵,
∴甲方案优惠;
(3)当时,
乙方案:(元),
甲方案:(元),
∵,
∴乙方案优惠.
【点睛】本题主要考查代数式的计算,根据题意选择有效数据列出代数式是解题的关键.
32.(1)
(2);改变,见解析
【分析】(1)根据图形,把阴影的面积表示出来,化简即可解得.
(2)把当和分别代入求值,分情况讨论即可解得.
【详解】(1)
(2)当时,
当时,
∴结论改变.
当时,
当时,
当时,
【点睛】此题考查了列代数式求阴影的面积,解题的关键是把阴影部分的面积表示出来.
33.(1); (2) ; (3)n+1或 .
【分析】(1)利用题中的方法设S=1+2+22+…+29,两边乘以2得到2S=2+22+…+29,然后把两式相减计算出S即可;
(2)利用题中的方法设S=1+3+32+33+34+…+310 ,两边乘以3得到3S=3+32+33+34+35+…+311 ,然后把两式相减计算出S即可;
(3)利用(2)的方法计算.
【详解】(1)设S=1+2+22+…+29①
则2S=2+22+…+210 ②
②-①得2S-S=S=210-1
∴S=1+2+22+…+29=210-1;
故答案为210-1
(2)设S=3+3+32+33+34+…+310 ①,
则3S=32+33+34+35+…+311 ②,
②-①得2S=311-3,
所以S=,
即3+32+33+34+…+310=;
故答案为;
(3)设S=1+a+a2+a3+a4+..+an①,
则aS=a+a2+a3+a4+..+an+an+1②,
②-①得:(a-1)S=an+1-1,
a=1时,不能直接除以a-1,此时原式等于n+1;
a不等于1时,a-1才能做分母,所以S=,
即1+a+a2+a3+a4+..+an=.
【点睛】本题考查了规律型:数字的变化类:认真观察、仔细思考,善用联想,利用类比的方法是解决这类问题的方法.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2023-2024学年度七年级上册数学第三章整式及其加减单元综合检测题
一、单选题
1.式子中,单项式有( )
A.1个 B.2个 C.3个 D.4个
2.下列各式符合代数式书写规则的是( )
A.a×5 B.a7 C. D.
3.某品牌冰箱进价为每台m元,提高20%作为标价.元旦期间按标价的9折出售,则出售一台这种冰箱可获得利润( )
A.m元 B.m元 C.m元 D.m元
4.多项式与多项式的和不含二次项,则m为( )
A.2 B. C.4 D.
5.如图,用规格相同的小棒按照图案规律摆放,2022根小棒最多可以摆出多少个小正方形?( )
A.503 B.124 C.808 D.252
6.如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点……按照此规律,第一百幅图中圆点的个数是( )
A.297 B.301 C.303 D.400
7.如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
A.2a﹣3b B.4a﹣8b C.2a﹣4b D.4a﹣10b
8.观察下列各式及其展开式
……
请你猜想的展开式从左往右第三项的系数是( )
A.35 B.45 C.55 D.66
二、填空题
9.单项式的系数是 ________,次数是_______.
10.多项式﹣3x+7是关于x的四次三项式,则m的值是_____.
11.按规律排列的单项式:﹣x,x3,﹣x5,x7,﹣x9,…,那么第15个单项式是 _____.
12.设甲数为x,乙数比甲数的3倍少6,则乙数用代数式表示为______.
13.一个三位数的十位为m,个位数比十位数的3倍多2,百位数比个位数少3,则这个三位数可表示为________.
14.若关于a,b的多项式中不含项,则m=_____.
15.若,则_____;
16.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a+b+c=____.
17.如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)
18.下面是一组数值转换机,写出(1)的输出结果_____(写在横线上),找出(2)的转换步骤(填写在框内)_____.
19.如图所示,南宋数学家杨辉在《详解九章算法》中出现的三角形状的数阵,又称为“杨辉三角形”.该三角形中的数据排列有着一定的规律,按此规律排列下去,第行的左边第个数是_____________.
20.已知,根据前面各式的规律,可得:_________;的值的个位数字是_______________.
21.观察下列等式:
;
;
;
;
;
根据以上等式总结规律并计算,则______.
三、解答题
22.计算
(1);
(2);
(3);
(4);
(5).
23.计算:
(1);
(2);
(3);
(4).
24.已知,,求:
(1)A+B;
(2)2A-B.
25.已知:,求的值.
26.化简:
(1)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b);
(2)5x2﹣[3x﹣2(2x﹣3)+7x2];
(3)先化简再求值:3a2b﹣[3a2b﹣(2abc﹣a2c)﹣4a2c]﹣abc.(若a=﹣2,b=﹣1,c=).
27.某同学做一道数学题:已知两个多项式A、B,计算,他误将“”看成“”,求得的结果是,已知,求的正确答案.
28.已知(m+3)x3y|m+1|是关于x,y的七次单项式,求m2﹣3m+1的值.
29.已知,a与b互为倒数,c与d互为相反数,求的值.
30.如图,若图中平面展开图折叠成正方体后,相对面上的两个数字互为相反数,求的值.
31.初一年级学生在名教师的带领下去公园秋游,公园的门票为每人元.现有两种优惠方案,甲方案:带队教师免费,学生按折收费;乙方案:师生都折收费.
若有名学生,用代数式表示两种优惠方案各需多少元?
当时,采用哪种方案优惠?
当时,采用哪种方案优惠?
32.如图,正方形和正方形的边长分别为a和6,点在一条直线上,点在一条直线上,将依次连接所围成的阴影部分的面积记为S阴影
(1)试用含a的代数式表示S阴影;
(2)当时,比较S阴影与面积的大小;当时,结论是否改变?为什么?
33.阅读下列材料:小明为了计算的值 ,采用以下方法:
设 ①
则 ②
②-①得
∴
(1)= ;
(2) = ;
(3)求的和( ,是正整数,请写出计算过程 ).
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据单项式定义逐个判断即可
【详解】解:题中的式子中单项式有、2x,共2个.
故选B.
【点睛】本题主要考查了单项式的定义,数字或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式.
2.D
【分析】根据代数式的书写要求判断各项.
【详解】解:A、数与字母相乘,数应该写在前边,乘号通常简写成“ ”或者省略不写,故此选项不符合题意;
B、数与字母相乘,数应该写在前边,故此选项不符合题意;
C、分数与字母相乘,带分数应该写成假分数的形式,故此选项不符合题意;
D、符合代数式的书写要求,故此选项符合题意.
故选:D.
【点睛】此题考查了代数式的书写,解题的关键是掌握代数式的书写要求.代数式的书写要求:(1)在代数式中出现的乘号,通常简写成“ ”或者省略不写;(2)数字与字母相乘时,数字要写在字母的前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写,带分数要写成假分数的形式.
3.D
【分析】先求出标价,再求出销售价,利用公式利润=售价-进价计算即可.
【详解】某品牌冰箱进价为每台m元,
提高20%作标价为:(1+20%)m元,
按标价的9折出售的售价为:1.2m×=1.08m元,
出售一台这种冰箱可获得利润=1.08m-m=0.08m元,
故答案为:D.
【点睛】本题考查销售利润问题,掌握标价,进价与利润率关系,标价折数与售价关系,售价进价与利润关系是解题关键.
4.C
【分析】由题意可以得到关于m的方程,解方程即可得到问题答案.
【详解】解:由题意可得:,
,
∵它们的和不含二次项
∴,
解之可得:,
故选:C.
【点睛】本题考查多项式的应用,熟练掌握多项式的相关概念是解题关键.
5.D
【分析】仔细观察发现,出现1个正六边形和1个小正方形时,需要小棒的根数是9根;出现2个正六边形和2个小正方形时,需要小棒的根数是17根;出现3个正六边形和3个小正方形时,需要小棒的根数是25根;……由此得出规律.
【详解】解:出现1个正六边形和1个小正方形时,需要小棒的根数是9根;
出现2个正六边形和2个小正方形时,需要小棒的根数是17根;
出现3个正六边形和3个小正方形时,需要小棒的根数是25根;
…,
则出现n个正六边形和n个小正方形时,需要小棒的根数是(8n+1)根;
(2022-1)÷8=252……5,
故选:D.
【点睛】本题主要考查图形的变化规律,根据图案的变化归纳出出现n个正六边形和n个小正方形时,需要小棒的根数是(8n+1)根是解题的关键.
6.B
【分析】首先根据前几个图形圆点的个数规律即可发现规律,从而得到第100个图摆放圆点的个数.
【详解】解:观察图形可知:第1幅图案需要4个圆点,即4+3×0,
第2幅图7个圆点,即4+3=4+3×1;
第3幅图10个圆点,即4+3+3=4+3×2;
第4幅图13个圆点,即4+3+3+3=4+3×3;
第n幅图中,圆点的个数为:4+3(n-1)=3n+1,
……,
第100幅图,圆中点的个数为:3×100+1=301.
故选:B.
【点睛】本题主要考查了图形的变化规律,解答的关键是由所给的图形总结出存在的规律.
7.B
【分析】剪下的两个小矩形的长为a b,宽为(a 3b),所以这两个小矩形拼成的新矩形的长为(a b),宽为(a 3b),然后计算这个新矩形的周长.
【详解】解:根据题意得:2(a﹣b+a﹣3b)=2(2a﹣4b)=4a﹣8b,
故选B.
【点睛】本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.解题的关键用a和b表示出剪下的两个小矩形的长与宽.
8.C
【分析】利用所给展开式探求各项系数的关系,特别是上面的展开式与下面的展开式中的各项系数的关系,可推出的展开式从左往右第三项的系数.
【详解】解:
∴依据规律可得到:
第三项的系数为1,
第三项的系数为,
第三项的系数为,
第三项的系数为:.
故选:C.
【点睛】此题考查了数字规律型,理解题意,找到系数的规律是解题的关键.
9.
【分析】直接根据单项式的系数与次数的定义得出答案,单项式中的数字因数叫做单项式的系数,一个单项式中所有字母的指数的和叫做单项式的次数.
【详解】解:单项式的系数和次数分别是:,.
故答案为:,6.
【点睛】本题考查了单项式的系数,单项式的次数,理解单项式的系数与次数是解题的关键.
10.5
【分析】根据多项式中次数最高的项的次数叫做多项式的次数进行分析即可.
【详解】解:∵多项式﹣3x+7是关于x的四次三项式,
∴m﹣1=4,
解得m=5,
故答案为:5.
【点睛】此题考查的是多项式的次数,掌握多项式的次数的定义是解决此题的关键.
11.
【分析】由题意可得第n个单项式是(﹣1)nx2n﹣1,当n=15时代入即可求解.
【详解】解:∵﹣x,x3,﹣x5,x7,﹣x9,…,
∴第n个单项式是(﹣1)nx2n﹣1,
∴第15个单项式是(﹣1)15x2×15﹣1
∴第15个单项式是﹣x29,
故答案为:﹣x29.
【点睛】本题考查数字的变化规律,根据所给的单项式的特点,探索出单项式的一般规律是解题的关键.
12.3x-6
【分析】根据题意列出代数式即可.
【详解】∵乙数比甲数的3倍少6,设甲数为x,
∴乙数是:3x-6.
故答案是:3x-6.
【点睛】考查了列代数式,解决问题的关键是读懂题意,找到所求的量的等量关系,列出代数式.
13.
【分析】根据题意先表示个位数为:再表示百位数为:从而可得答案.
【详解】解: 一个三位数的十位为m,个位数比十位数的3倍多2,百位数比个位数少3,
个位数为: 百位数为:
所以这个三位数为:
故答案为:
【点睛】本题考查的是列代数式,整式的加减运算,一个三位数的百位,十位,个位为分别为 则这个三位数表示为: 掌握列式的方法是解题的关键.
14.2
【分析】原式去括号合并得到最简结果,根据结果不含ab项,求出m的值即可.
【详解】原式,
由结果不含项,得到,
解得:.
故答案为:2.
【点睛】本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.
15.2029
【分析】先由,得,然后将变形为x[2(x2-2x)-3x+12]+2020,代入得x(-3x+6)+2020,再变形为-3(x2-2x)+2020,再代入则可求解.
【详解】解:∵,
∴,
∴
=x(2x2-4x-3x+12)+2020
=x[2(x2-2x)-3x+12]+2020
= x[2×(-3)-3x+12]+2020
=x(-3x+6)+2020
=-3(x2-2x)+2020
=-3×(-3)+2020
=9+2020
=2029
故答案为:2029.
【点睛】本题考查代数式求值,将代数式变形为已知式子形式是解题的关键.
16.110
【详解】试题分析:根据前三个正方形中的数字规律可知:C所处的位置上的数字是连续的奇数,所以c=9,而a所处的位置上的数字是连续的偶数,所以a=10,而b=ac+1=9×10+1=91,所以a+b+c=9+10+91=110.
考点:数字规律.
17.4n+3
【分析】利用给出的三个图形寻找规律,发现白色正方形个数=总的正方形个数-黑色正方形个数,而黑色正方形个数第1个为1,第二个为2,由此寻找规律,总个数只要找到边与黑色正方形个数之间关系即可,依此类推,寻找规律.
【详解】解:方法一:
第1个图形黑、白两色正方形共3×3个,其中黑色1个,白色3×3-1个,
第2个图形黑、白两色正方形共3×5个,其中黑色2个,白色3×5-2个,
第3个图形黑、白两色正方形共3×7个,其中黑色3个,白色3×7-3个,
依此类推,
第n个图形黑、白两色正方形共3×(2n+1)个,其中黑色n个,白色3×(2n+1)-n个,
即:白色正方形5n+3个,黑色正方形n个,
故第n个图案中白色正方形比黑色正方形多4n+3个,
方法二
第1个图形白色正方形共8个,黑色1个,白色比黑色多7个,
第2个图形比第1个图形白色比黑色又多了4个,即白色比黑色多(7+4)个,
第3个图形比第2个图形白色比黑色又多了4个,即白色比黑色多(7+4×2)个,
类推,第n个图案中白色正方形比黑色正方形多[7+4(n-1)]个,即(4n+3)个,
故第n个图案中白色正方形比黑色正方形多4n+3个.
【点睛】本题考查了几何图形的变化规律,是探索型问题,图中的变化规律是解题的关键.
18. 2x-3 +3;2
【分析】根据图(1)可得:2x﹣3;图(2)中所表现出来的规律是x先加3,然后再让x加3的和除以2,即(x+3)÷2=.
【详解】(1)先算乘法,再减3,为:2x﹣3;
(2)先算加法,再除以2.先填“+3”,接下来填“÷2”.
故答案为(1)2x-3;(2)+3;2.
【点睛】要学会读图,能从图中找到规律,例如,(1)中所揭示的规律为:2x﹣3;(2)中可由结果判断出是x先加2,然后再让x加3的和除以2,此题主要考查阅读思考能力的灵活性.
19.
【分析】观察前几行左边第个数的排列规律,进而推出第100行的左边第个数.
【详解】解:从第3行开始:
第3行:左边第个数是1==;
第4行:左边第个数是3==;
第5行:左边第个数是6==;
第6行:左边第个数是10==;
……
第100行:左边第个数是==4851.
故答案为:4851.
【点睛】本题的关键是找出从第3行开始,每行的左边第3个数的排列规律:1,3,6,10,15…,进而得出第n行左边第个数是,由此得解.
20. ; 7
【分析】仿照阅读材料中的等式写出的结果即可;利用得出的规律化简,计算即可求出值.
【详解】解:由题意可得:;
由以上过程可知:,
∴,
∵,个位数字为2,,个位数字为4,,个位数字为8,,个位数字为6;
,个位数字为2,,个位数字为4,,个位数字为8,,个位数字为6;
…;
∴的各位数字与的各位数字相同,都是8,
∴的值的个位数字是8-1=7.
故答案为:; 7.
【点睛】本题考查规律问题等知识,解题的关键是学会或转化的思想思考问题,学会从特殊到一般的探究规律的方法.
21.255
【分析】根据所给出的等式找到规律,再利用式子的规律进行逆用即可求解.
【详解】解:由给出等式可知,,
∴
故答案为:255.
【点睛】本题考查数字的变化规律,能够根据题中所给式子探索出式子的规律是解题的关键.
22.(1)2ab;
(2);
(3);
(4);
(5)
【分析】原式各项去括号合并即可得到结果.
(1)=2ab;
(2)==;
(3)==;
(4)==;
(5)==.
【点睛】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.
23.(1);(2);(3);(4).
【分析】(1)先去括号,然后再合并同类项即可;
(2)先去括号,然后再合并同类项即可;
(3)先去括号,然后再合并同类项即可;
(4)先去括号,然后再合并同类项即可.
【详解】解:(1)
=
=
=;
(2)
=
=
=;
(3)
=
=
=;
(4)
=
=
=.
【点睛】本题主要考查了整式的加减运算,掌握去括号法则和合并同类项法则成为解答本题的关键.
24.(1)-2x+3
(2)
【分析】(1)根据整式加法的运算法则计算即可;
(2)根据整式减法的运算法则计算即可;
【详解】(1)
;
(2)
【点睛】本题考查整式的加法和减法.掌握整式的加法和减法的运算法则是解题关键.
25.;
【分析】先根据绝对值和平方的非负性求出x,y,再根据整式的混和运算法则化成最简,然后代入数值计算即可.
【详解】解:∵,
,
解得:,,
∴原式
.
当,时,
原式
.
【点睛】本题主要考查了整式的化简求值,根据非负性求出x,y的值是解题的关键.
26.(1)
(2)
(3)abc+3a2c,7
【分析】(1)先去括号,然后合并同类项,即可得到答案;
(2)先去括号,然后合并同类项,即可得到答案;
(3)先去括号,然后合并同类项进行化简,再把a=﹣2,b=﹣1,c=代入计算,即可求出答案.
【详解】(1)解:原式=
=;
(2)解:原式=
=
=;
(3)解:3a2b﹣[3a2b﹣(2abc﹣a2c)﹣4a2c]﹣abc
=3a2b﹣3a2b+(2abc﹣a2c)+4a2c﹣abc
=3a2b﹣3a2b+2abc﹣a2c+4a2c﹣abc
=abc+3a2c,
当a=﹣2,b=﹣1,时,
原式=﹣2×(﹣1)×+3×(﹣2)2×=1+6=7;
【点睛】本题考查了整式的加减运算,整式的化简求值,解题的关键是熟练掌握运算法则,正确的进行化简.
27.
【分析】根据题意得,求出A的值,代入后求出即可.
【详解】解:∵
,
∴
.
【点睛】本题考查了整式的加减的应用,关键是求出A的值.
28.1或41
【分析】直接利用单项式的系数和次数确定方法分析得出答案.
【详解】解:∵(m+3)x3y|m+1|是关于x,y的七次单项式,
∴3+|m+1|=7且m+3≠0,
解得:m=3,或m=﹣5,
∴m2﹣3m+1=9﹣9+1=1,
或m2﹣3m+1=25+15+1=41.
故m2﹣3m+1的值是1或41.
【点睛】此题主要考查了单项式,正确把握单项式的系数和次数确定方法是解题关键.
29.-2
【分析】根据绝对值的性质、平方的性质可知,,再由相反数的性质,倒数的性质得出ab、c+d的值,再代入代数式计算可得.
【详解】解:,
,
,
因为与互为倒数,所以
因为与互为相反数,所以
原式
=-2.
【点睛】本题主要考查非负数的性质,互为倒数,互为相反数,代数式求值,含乘方的有理数混合运算,解题的关键是熟练掌握混合运算顺序和运算法则.
30.
【分析】根据正方体的展开图,判断出相对的面,利用相对面上的两个数字互为相反数,求出x、y、z,进而计算出x-y+z的值即可.
【详解】解:由题意得与,与,与分别是相对面上的两个数,
所以,,,
所以.
【点睛】考查正方体的展开与折叠,正方体的展开图中“相间、Z端是对面”判断对面.
31.(1) 甲16m, 乙:;(2) 甲方案优惠,理由见解析;(3) 乙方案优惠,理由见解析
【分析】 根据题意确定两种优惠方案所需的钱数;
把代入计算,比较即可;
把代入计算,比较即可得到答案.
【详解】解:甲方案需要的钱数为:,
乙方案需要的钱数为:;
当时,
乙方案:(元),
甲方案:(元),
∵,
∴甲方案优惠;
(3)当时,
乙方案:(元),
甲方案:(元),
∵,
∴乙方案优惠.
【点睛】本题主要考查代数式的计算,根据题意选择有效数据列出代数式是解题的关键.
32.(1)
(2);改变,见解析
【分析】(1)根据图形,把阴影的面积表示出来,化简即可解得.
(2)把当和分别代入求值,分情况讨论即可解得.
【详解】(1)
(2)当时,
当时,
∴结论改变.
当时,
当时,
当时,
【点睛】此题考查了列代数式求阴影的面积,解题的关键是把阴影部分的面积表示出来.
33.(1); (2) ; (3)n+1或 .
【分析】(1)利用题中的方法设S=1+2+22+…+29,两边乘以2得到2S=2+22+…+29,然后把两式相减计算出S即可;
(2)利用题中的方法设S=1+3+32+33+34+…+310 ,两边乘以3得到3S=3+32+33+34+35+…+311 ,然后把两式相减计算出S即可;
(3)利用(2)的方法计算.
【详解】(1)设S=1+2+22+…+29①
则2S=2+22+…+210 ②
②-①得2S-S=S=210-1
∴S=1+2+22+…+29=210-1;
故答案为210-1
(2)设S=3+3+32+33+34+…+310 ①,
则3S=32+33+34+35+…+311 ②,
②-①得2S=311-3,
所以S=,
即3+32+33+34+…+310=;
故答案为;
(3)设S=1+a+a2+a3+a4+..+an①,
则aS=a+a2+a3+a4+..+an+an+1②,
②-①得:(a-1)S=an+1-1,
a=1时,不能直接除以a-1,此时原式等于n+1;
a不等于1时,a-1才能做分母,所以S=,
即1+a+a2+a3+a4+..+an=.
【点睛】本题考查了规律型:数字的变化类:认真观察、仔细思考,善用联想,利用类比的方法是解决这类问题的方法.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
