3.2.2函数的奇偶性 课件-2023-2024学年高一上学期数学人教A版(2019)必修第一册(共20张PPT)
文档属性
| 名称 | 3.2.2函数的奇偶性 课件-2023-2024学年高一上学期数学人教A版(2019)必修第一册(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 422.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
函数的奇偶性
生活中的对称
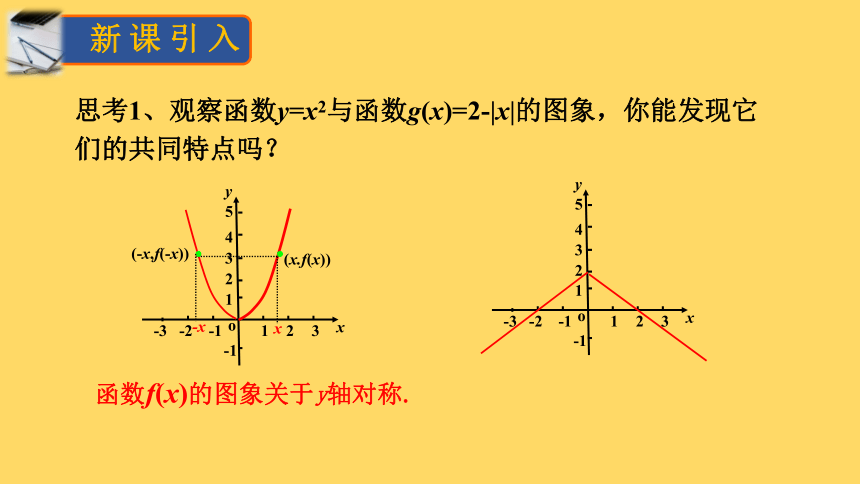
思考1、观察函数y=x2与函数g(x)=2-|x|的图象,你能发现它们的共同特点吗?
新课引入
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
(x.f(x))
-x
x
(-x,f(-x))
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
函数f(x)的图象关于y轴对称.
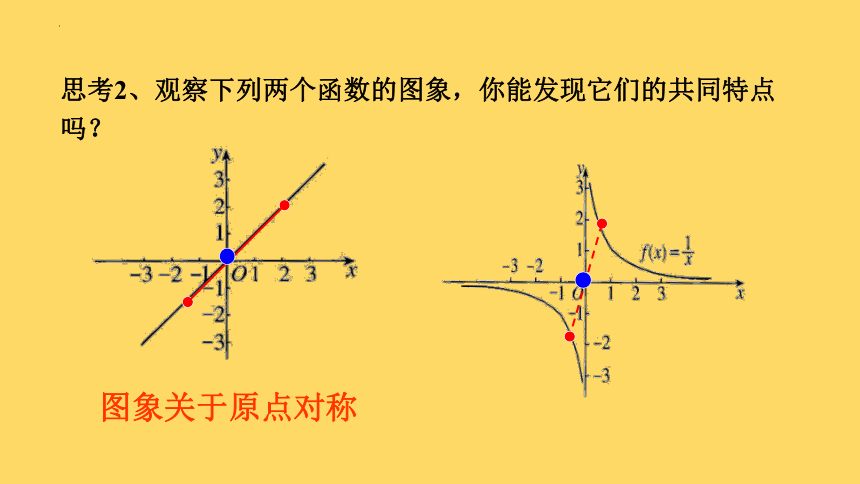
思考2、观察下列两个函数的图象,你能发现它们的共同特点吗?
图象关于原点对称
一般地,设函数f(x)的定义域为I,如果 x∈I.都-x∈I,且f(-x)=f(x).那么函数f(x)就叫做偶函数.
偶函数
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
(x.f(x))
-x
x
(-x,f(-x))
例如f(x)=x2:
注意:
1、定义域关于原点对称
2、图像关于y轴对称,即f(-x)=f(x)
奇函数
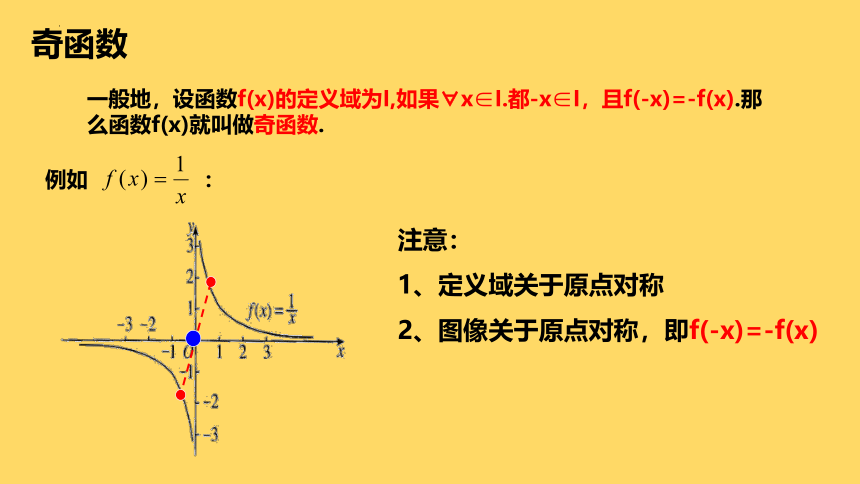
一般地,设函数f(x)的定义域为I,如果 x∈I.都-x∈I,且f(-x)=-f(x).那么函数f(x)就叫做奇函数.
例如 :
注意:
1、定义域关于原点对称
2、图像关于原点对称,即f(-x)=-f(x)
用奇偶性作为分类标准, 可以将函数分为:
奇函数
偶函数
非奇非偶函数
既奇又偶函数
则有f(0)=0
又是奇函数
例题讲解
例1、
1、奇、偶函数的定义域一定关于原点对称;
2、若f(x)为奇函数,且0在定义域内,则一定有f(0)=0
3、奇、偶函数的图象特征:
偶函数的图象关于y轴对称,
奇函数的图象关于原点对称.
总结
例题讲解
(3) 根据定义下结论.
(1) 先求定义域,看是否关于原点对称;
(2) 再判断f (-x)=-f (x)或f (-x)=f (x)是否恒成立;
一、判断函数的奇偶性的方法:
图像法
定义法
二、根据定义判断函数的奇偶性的步骤:
总结
巩固练习
偶函数 奇函数
定义
图象
定义域
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),
关于y轴对称
关于原点对称
关于原点对称
课堂小结
用定义法判断函数的奇偶性的步骤:
①首先确定函数的定义域,
并判断其定义域是否关于原点对称;
②确定f(-x)和f(x)的关系;
③作出相应结论。
课堂小结
函数的奇偶性
生活中的对称
思考1、观察函数y=x2与函数g(x)=2-|x|的图象,你能发现它们的共同特点吗?
新课引入
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
(x.f(x))
-x
x
(-x,f(-x))
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
函数f(x)的图象关于y轴对称.
思考2、观察下列两个函数的图象,你能发现它们的共同特点吗?
图象关于原点对称
一般地,设函数f(x)的定义域为I,如果 x∈I.都-x∈I,且f(-x)=f(x).那么函数f(x)就叫做偶函数.
偶函数
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
(x.f(x))
-x
x
(-x,f(-x))
例如f(x)=x2:
注意:
1、定义域关于原点对称
2、图像关于y轴对称,即f(-x)=f(x)
奇函数
一般地,设函数f(x)的定义域为I,如果 x∈I.都-x∈I,且f(-x)=-f(x).那么函数f(x)就叫做奇函数.
例如 :
注意:
1、定义域关于原点对称
2、图像关于原点对称,即f(-x)=-f(x)
用奇偶性作为分类标准, 可以将函数分为:
奇函数
偶函数
非奇非偶函数
既奇又偶函数
则有f(0)=0
又是奇函数
例题讲解
例1、
1、奇、偶函数的定义域一定关于原点对称;
2、若f(x)为奇函数,且0在定义域内,则一定有f(0)=0
3、奇、偶函数的图象特征:
偶函数的图象关于y轴对称,
奇函数的图象关于原点对称.
总结
例题讲解
(3) 根据定义下结论.
(1) 先求定义域,看是否关于原点对称;
(2) 再判断f (-x)=-f (x)或f (-x)=f (x)是否恒成立;
一、判断函数的奇偶性的方法:
图像法
定义法
二、根据定义判断函数的奇偶性的步骤:
总结
巩固练习
偶函数 奇函数
定义
图象
定义域
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),
关于y轴对称
关于原点对称
关于原点对称
课堂小结
用定义法判断函数的奇偶性的步骤:
①首先确定函数的定义域,
并判断其定义域是否关于原点对称;
②确定f(-x)和f(x)的关系;
③作出相应结论。
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
