28.1 锐角三角函数(课时2)同步练习 人教版数学九年级下册(含答案)
文档属性
| 名称 | 28.1 锐角三角函数(课时2)同步练习 人教版数学九年级下册(含答案) | 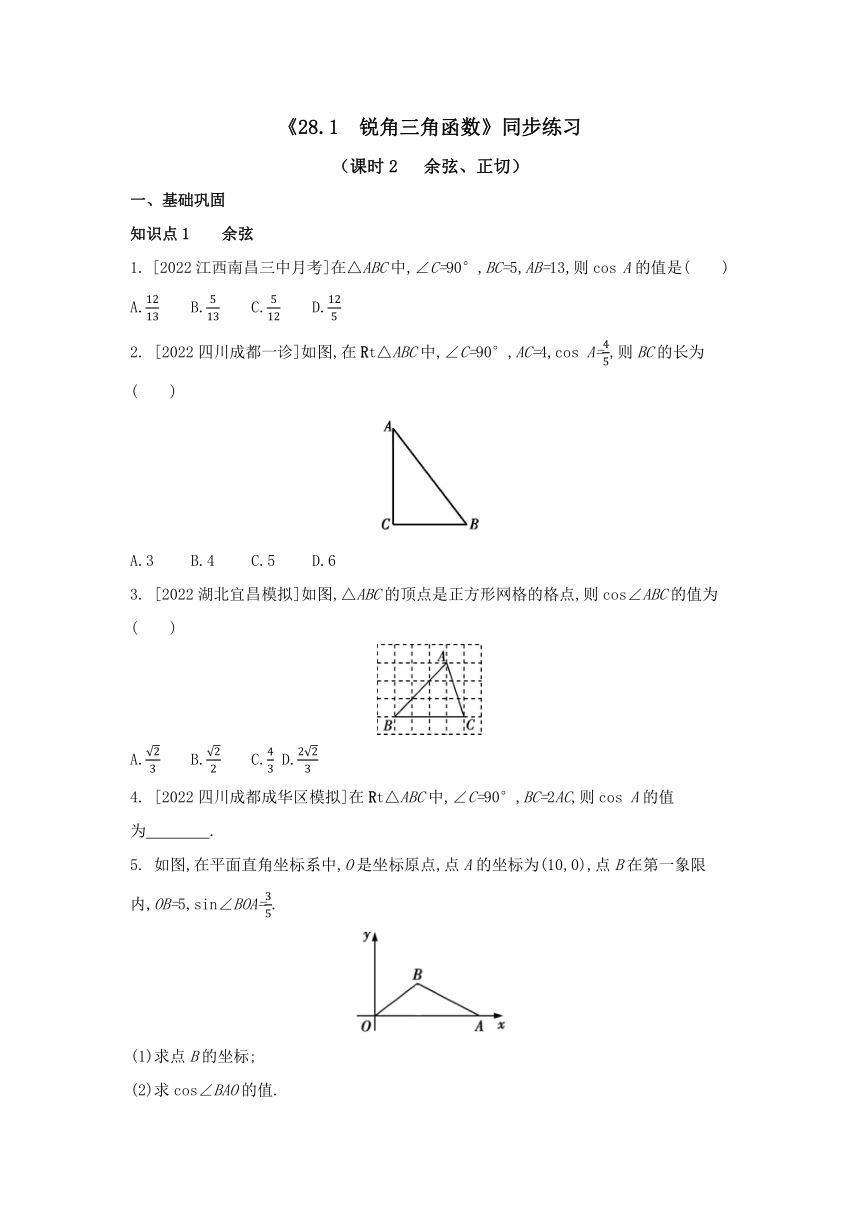 | |
| 格式 | docx | ||
| 文件大小 | 277.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 16:19:25 | ||
图片预览


文档简介
《28.1 锐角三角函数》同步练习
(课时2 余弦、正切)
一、基础巩固
知识点1 余弦
1. [2022江西南昌三中月考]在△ABC中,∠C=90°,BC=5,AB=13,则cos A的值是( )
A. B. C. D.
2. [2022四川成都一诊]如图,在Rt△ABC中,∠C=90°,AC=4,cos A=,则BC的长为( )
A.3 B.4 C.5 D.6
3. [2022湖北宜昌模拟]如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为( )
A. B. C. D.
4. [2022四川成都成华区模拟]在Rt△ABC中,∠C=90°,BC=2AC,则cos A的值为 .
5. 如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(10,0),点B在第一象限内,OB=5,sin∠BOA=.
(1)求点B的坐标;
(2)求cos∠BAO的值.
知识点2 正切
6. 如图,网格中小正方形的边长均为1,△ABC的三个顶点均在格点上,则tan A的值为( )
A. B. C. D.
7. [2022湖南常德模拟]如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于点H,则tan∠POH的值为( )
A. B. C.1 D.
8. [2022山东烟台模拟]已知直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 .
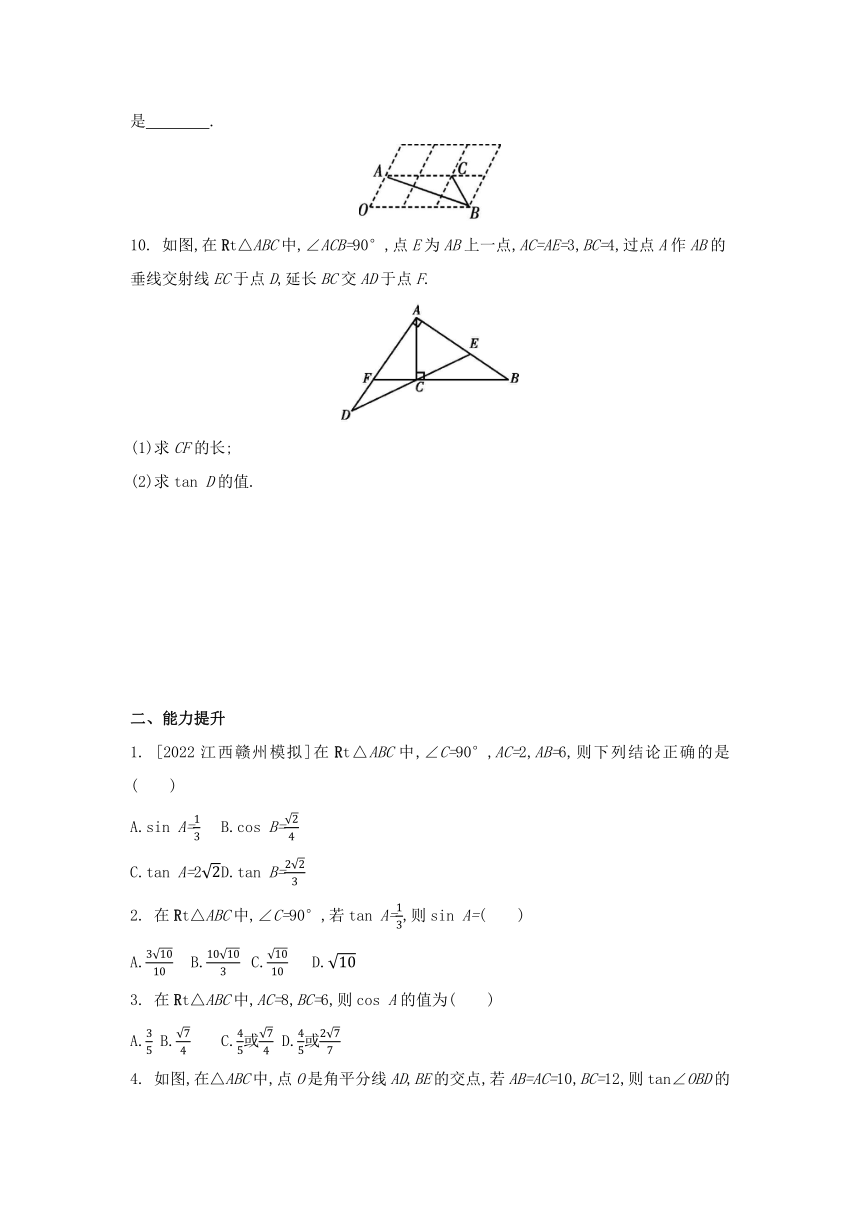
9. [2022福建泉州七中月考]如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(如∠O)为60°,A,B,C 都在格点上,则tan∠ABC的值是 .
10. 如图,在Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求tan D的值.
二、能力提升
1. [2022江西赣州模拟]在Rt△ABC中,∠C=90°,AC=2,AB=6,则下列结论正确的是( )
A.sin A= B.cos B=
C.tan A=2 D.tan B=
2. 在Rt△ABC中,∠C=90°,若tan A=,则sin A=( )
A. B. C. D.
3. 在Rt△ABC中,AC=8,BC=6,则cos A的值为( )
A. B. C.或 D.或
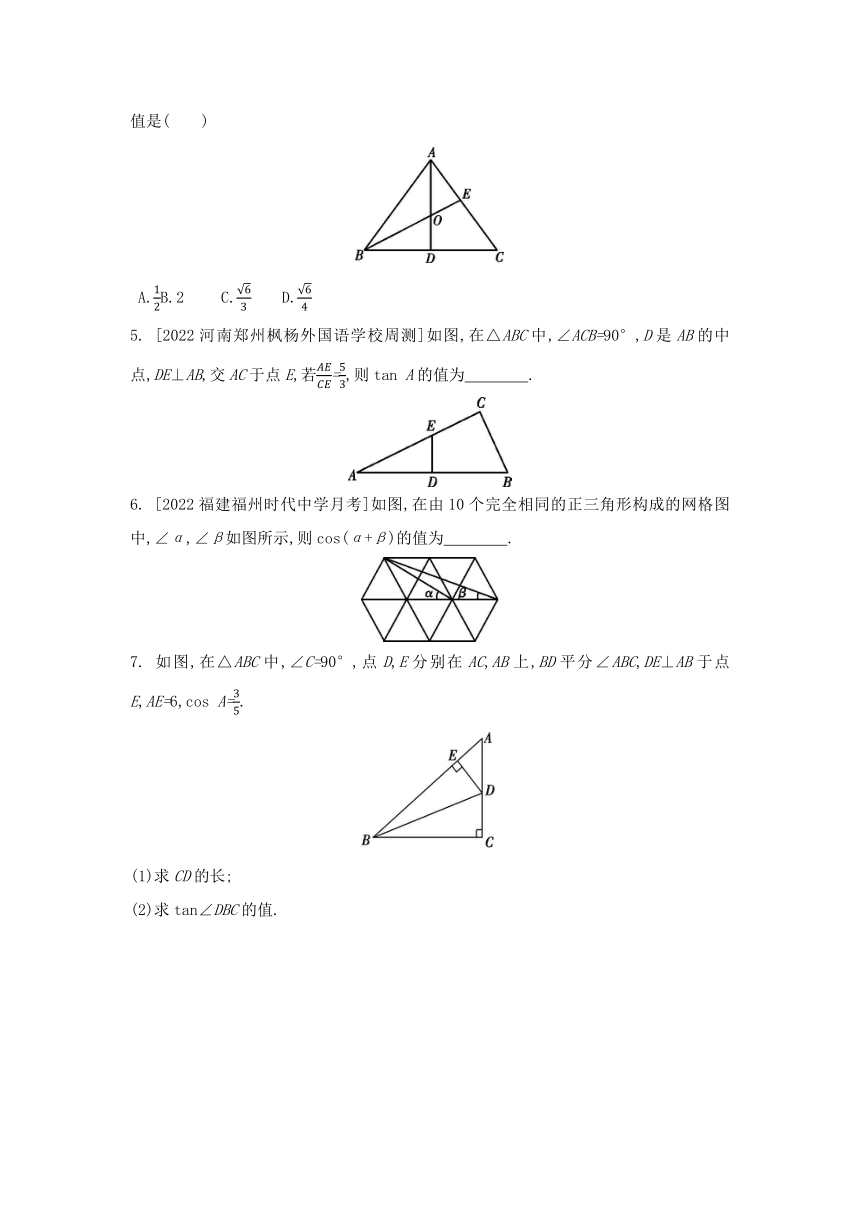
4. 如图,在△ABC中,点O是角平分线AD,BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A. B.2 C. D.
5. [2022河南郑州枫杨外国语学校周测]如图,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB,交AC于点E,若=,则tan A的值为 .
6. [2022福建福州时代中学月考]如图,在由10个完全相同的正三角形构成的网格图中,∠α,∠β如图所示,则cos(α+β)的值为 .
7. 如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,BD平分∠ABC,DE⊥AB于点E,AE=6,cos A=.
(1)求CD的长;
(2)求tan∠DBC的值.
8. 如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,BC=3,AB=8,CD=5.
(1)求梯形ABCD的面积;
(2)连接BD,求∠DBC的正切值.
参考答案
一、基础巩固
1.A 在△ABC中,∵∠C=90°,BC=5,AB=13,∴AC==12,∴cos A==.
2.A 在Rt△ABC中,∵∠C=90°,cos A=,∴=.∵AC=4,∴AB=5,∴BC==3.
3.B 如图,过点A作AD⊥BC于点D,由题意可知点D位于格点上,设网格中小正方形的边长均为1,则AD=BD=3,AB=3,∴cos∠ABC===.
4. 设AC=a(a>0),则BC=2a,∵∠C=90°,∴AB==a,∴cos A===.
5.(1)如图,过点B作BC⊥OA于点C.
∵OB=5,sin∠BOA=,∴BC=3,
∴OC===4,
又点B在第一象限内,
∴点B的坐标为(4,3).
(2)∵A(10,0),OC=4,∴AC=6,
∴AB===3.
∴cos∠BAO===.
6.D 由题图,可知BC=4,AB=3,则tan A==.
7.B ∵点P(12,a)在反比例函数y=的图象上,∴a==5.∵PH⊥x轴,∴PH=5,OH=12,∴tan∠POH==.
8. 由折叠的性质,知BE=AE.设CE=x,则BE=AE=8-x.在Rt△BCE中,由勾股定理,得BE2=BC2+CE2,即(8-x)2=62+x2,解得x=,∴CE=,∴tan∠CBE==.
9. 如图,连接EA,EC,易知E,C,B三点共线.设菱形的边长为a,由题意得∠AEF=30°,∠BEF=60°,AE=a,EB=2a,∴∠AEB=90°,∴tan∠ABC===.
10.(1)∵∠ACB=90°,∴∠B+∠BAC=90°.
∵AD⊥AB,∴∠BAC+∠CAF=90°,∴∠B=∠CAF.
∵tan B==,
∴tan∠CAF==,∴CF=AC=.
(2)如图,过点C作CH⊥AB于点H.
∵DA⊥AB,∴CH∥AD,∴∠D=∠ECH.
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,由勾股定理,得AB=5.
∵S△ABC=AC·BC=AB·CH,∴CH==,
∴AH==,∴EH=AE-AH=,
∴tan D=tan∠ECH==.
二、能力提升
1.C 在Rt△ABC中,∵∠C=90°,AC=2,AB=6,∴BC==4,∴sin A===,
cos B===,tan A===2,tan B===,故A,B,D错误,C正确.
2.C ∵tan A==,∴设BC=k,则AC=3k,根据勾股定理,得AB==k,∴sin A===.
3.C ①当∠C=90°时,由勾股定理,得AB==10,∴cos A===;②当∠B=90°时,由勾股定理,得AB==2,∴cos A===.综上所述,cos A的值为或.
4.A 如图,过点O作OF⊥AB于点F,∵AB=AC,AD平分∠BAC,∴AD⊥BC,BD=CD=BC=6,∴AD==8.∵BE平分∠ABC,∴OF=OD,BF=BD=6,∴AF=AB-BF=4.设OD=OF=x,则AO=AD-OD=8-x,在Rt△AOF中,由勾股定理,得x2+42=(8-x)2,∴x=3,∴OD=3.在Rt△OBD中,
tan∠OBD==.
5. 由D是AB的中点且DE⊥AB,得到ED垂直平分AB,从而想到连接EB,如图,则AE=BE,所以==.设EC=3k,则AE=BE=5k,AC=5k+3k=8k.在Rt△BCE中,BC==4k.在Rt△ABC中,∠ACB=90°,tan A===.
6. 如图,连接DE.在△ABC中,∠ABC=120°,BA=BC,∴∠α=30°.同理,可得∠CDE=∠CED=30°=∠α,∴∠α+∠β=∠CDE+∠β=∠ADE.∵∠AEC=60°,∴∠AED=∠AEC+∠CED=90°.设每个正三角形的边长为a,则AE=2a,DE=a,∴AD==a,∴cos(α+β)=cos∠ADE==.
7. (1)在Rt△ADE中,因为AE=6,cos A=,
所以AD==10,
由勾股定理,得DE===8.
因为DE⊥AB,DC⊥BC,且BD平分∠ABC,
所以CD=DE=8.
(2)由(1)得AC=AD+CD=18,
在△ABC中,因为∠C=90°,所以cos A==,所以AB=30,
由勾股定理,得BC===24,
所以tan∠DBC===.
8.(1)如图,过点C作CE⊥AB于点E,
则四边形AECD是矩形,
∴CE=AD,AE=DC=5,∴BE=8-5=3,
∴AD=CE===6,
∴S梯形ABCD=×(CD+AB)×AD=×(5+8)×6=39.
(2)如图,过点C作CF⊥BD于点F.
根据勾股定理,可得BD===10.
∵S△BCD=×BD×CF=DC×CE,
∴10×CF=5×6,∴CF=3,
∴BF===6,
∴tan∠DBC===.
故∠DBC的正切值为.
(课时2 余弦、正切)
一、基础巩固
知识点1 余弦
1. [2022江西南昌三中月考]在△ABC中,∠C=90°,BC=5,AB=13,则cos A的值是( )
A. B. C. D.
2. [2022四川成都一诊]如图,在Rt△ABC中,∠C=90°,AC=4,cos A=,则BC的长为( )
A.3 B.4 C.5 D.6
3. [2022湖北宜昌模拟]如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为( )
A. B. C. D.
4. [2022四川成都成华区模拟]在Rt△ABC中,∠C=90°,BC=2AC,则cos A的值为 .
5. 如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(10,0),点B在第一象限内,OB=5,sin∠BOA=.
(1)求点B的坐标;
(2)求cos∠BAO的值.
知识点2 正切
6. 如图,网格中小正方形的边长均为1,△ABC的三个顶点均在格点上,则tan A的值为( )
A. B. C. D.
7. [2022湖南常德模拟]如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于点H,则tan∠POH的值为( )
A. B. C.1 D.
8. [2022山东烟台模拟]已知直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 .
9. [2022福建泉州七中月考]如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(如∠O)为60°,A,B,C 都在格点上,则tan∠ABC的值是 .
10. 如图,在Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求tan D的值.
二、能力提升
1. [2022江西赣州模拟]在Rt△ABC中,∠C=90°,AC=2,AB=6,则下列结论正确的是( )
A.sin A= B.cos B=
C.tan A=2 D.tan B=
2. 在Rt△ABC中,∠C=90°,若tan A=,则sin A=( )
A. B. C. D.
3. 在Rt△ABC中,AC=8,BC=6,则cos A的值为( )
A. B. C.或 D.或
4. 如图,在△ABC中,点O是角平分线AD,BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A. B.2 C. D.
5. [2022河南郑州枫杨外国语学校周测]如图,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB,交AC于点E,若=,则tan A的值为 .
6. [2022福建福州时代中学月考]如图,在由10个完全相同的正三角形构成的网格图中,∠α,∠β如图所示,则cos(α+β)的值为 .
7. 如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,BD平分∠ABC,DE⊥AB于点E,AE=6,cos A=.
(1)求CD的长;
(2)求tan∠DBC的值.
8. 如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,BC=3,AB=8,CD=5.
(1)求梯形ABCD的面积;
(2)连接BD,求∠DBC的正切值.
参考答案
一、基础巩固
1.A 在△ABC中,∵∠C=90°,BC=5,AB=13,∴AC==12,∴cos A==.
2.A 在Rt△ABC中,∵∠C=90°,cos A=,∴=.∵AC=4,∴AB=5,∴BC==3.
3.B 如图,过点A作AD⊥BC于点D,由题意可知点D位于格点上,设网格中小正方形的边长均为1,则AD=BD=3,AB=3,∴cos∠ABC===.
4. 设AC=a(a>0),则BC=2a,∵∠C=90°,∴AB==a,∴cos A===.
5.(1)如图,过点B作BC⊥OA于点C.
∵OB=5,sin∠BOA=,∴BC=3,
∴OC===4,
又点B在第一象限内,
∴点B的坐标为(4,3).
(2)∵A(10,0),OC=4,∴AC=6,
∴AB===3.
∴cos∠BAO===.
6.D 由题图,可知BC=4,AB=3,则tan A==.
7.B ∵点P(12,a)在反比例函数y=的图象上,∴a==5.∵PH⊥x轴,∴PH=5,OH=12,∴tan∠POH==.
8. 由折叠的性质,知BE=AE.设CE=x,则BE=AE=8-x.在Rt△BCE中,由勾股定理,得BE2=BC2+CE2,即(8-x)2=62+x2,解得x=,∴CE=,∴tan∠CBE==.
9. 如图,连接EA,EC,易知E,C,B三点共线.设菱形的边长为a,由题意得∠AEF=30°,∠BEF=60°,AE=a,EB=2a,∴∠AEB=90°,∴tan∠ABC===.
10.(1)∵∠ACB=90°,∴∠B+∠BAC=90°.
∵AD⊥AB,∴∠BAC+∠CAF=90°,∴∠B=∠CAF.
∵tan B==,
∴tan∠CAF==,∴CF=AC=.
(2)如图,过点C作CH⊥AB于点H.
∵DA⊥AB,∴CH∥AD,∴∠D=∠ECH.
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,由勾股定理,得AB=5.
∵S△ABC=AC·BC=AB·CH,∴CH==,
∴AH==,∴EH=AE-AH=,
∴tan D=tan∠ECH==.
二、能力提升
1.C 在Rt△ABC中,∵∠C=90°,AC=2,AB=6,∴BC==4,∴sin A===,
cos B===,tan A===2,tan B===,故A,B,D错误,C正确.
2.C ∵tan A==,∴设BC=k,则AC=3k,根据勾股定理,得AB==k,∴sin A===.
3.C ①当∠C=90°时,由勾股定理,得AB==10,∴cos A===;②当∠B=90°时,由勾股定理,得AB==2,∴cos A===.综上所述,cos A的值为或.
4.A 如图,过点O作OF⊥AB于点F,∵AB=AC,AD平分∠BAC,∴AD⊥BC,BD=CD=BC=6,∴AD==8.∵BE平分∠ABC,∴OF=OD,BF=BD=6,∴AF=AB-BF=4.设OD=OF=x,则AO=AD-OD=8-x,在Rt△AOF中,由勾股定理,得x2+42=(8-x)2,∴x=3,∴OD=3.在Rt△OBD中,
tan∠OBD==.
5. 由D是AB的中点且DE⊥AB,得到ED垂直平分AB,从而想到连接EB,如图,则AE=BE,所以==.设EC=3k,则AE=BE=5k,AC=5k+3k=8k.在Rt△BCE中,BC==4k.在Rt△ABC中,∠ACB=90°,tan A===.
6. 如图,连接DE.在△ABC中,∠ABC=120°,BA=BC,∴∠α=30°.同理,可得∠CDE=∠CED=30°=∠α,∴∠α+∠β=∠CDE+∠β=∠ADE.∵∠AEC=60°,∴∠AED=∠AEC+∠CED=90°.设每个正三角形的边长为a,则AE=2a,DE=a,∴AD==a,∴cos(α+β)=cos∠ADE==.
7. (1)在Rt△ADE中,因为AE=6,cos A=,
所以AD==10,
由勾股定理,得DE===8.
因为DE⊥AB,DC⊥BC,且BD平分∠ABC,
所以CD=DE=8.
(2)由(1)得AC=AD+CD=18,
在△ABC中,因为∠C=90°,所以cos A==,所以AB=30,
由勾股定理,得BC===24,
所以tan∠DBC===.
8.(1)如图,过点C作CE⊥AB于点E,
则四边形AECD是矩形,
∴CE=AD,AE=DC=5,∴BE=8-5=3,
∴AD=CE===6,
∴S梯形ABCD=×(CD+AB)×AD=×(5+8)×6=39.
(2)如图,过点C作CF⊥BD于点F.
根据勾股定理,可得BD===10.
∵S△BCD=×BD×CF=DC×CE,
∴10×CF=5×6,∴CF=3,
∴BF===6,
∴tan∠DBC===.
故∠DBC的正切值为.
