人教版八年级数学上册11.1.1三角形的边 课件 (共21张ppt)
文档属性
| 名称 | 人教版八年级数学上册11.1.1三角形的边 课件 (共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 917.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 16:58:26 | ||
图片预览






文档简介
11.1.1三角形的边
学习目标
1.认识三角形的概念及三角形的基本要素。
2.理解三角形三条边之间的关系,会给三角形分类。
知识点1 三角形的概念
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形,三角形用符号“△”表示,读作“三角形”。
组成三角形的三条线段叫做三角形的边;相邻两边的公共端点叫做三角形的顶点;相邻两边的夹角叫做三角形的内角。
知识点1 三角形的概念
用数学语言描述如图所示的三角形,顶点是A,B,C的三角形记作△ABC,读作“三角形ABC”,三角形有三个顶点:A,B,C;有三条边:AB,BC,AC;有三个内角:∠A,∠B,∠C。
通常当△ABC的三边用a,b,c表示时,顶点A所对的边BC用a表示,顶点B所对的边AC用b表示,顶点C所对的边AB用c表示。
c
b
a
C
B
A
例题讲解
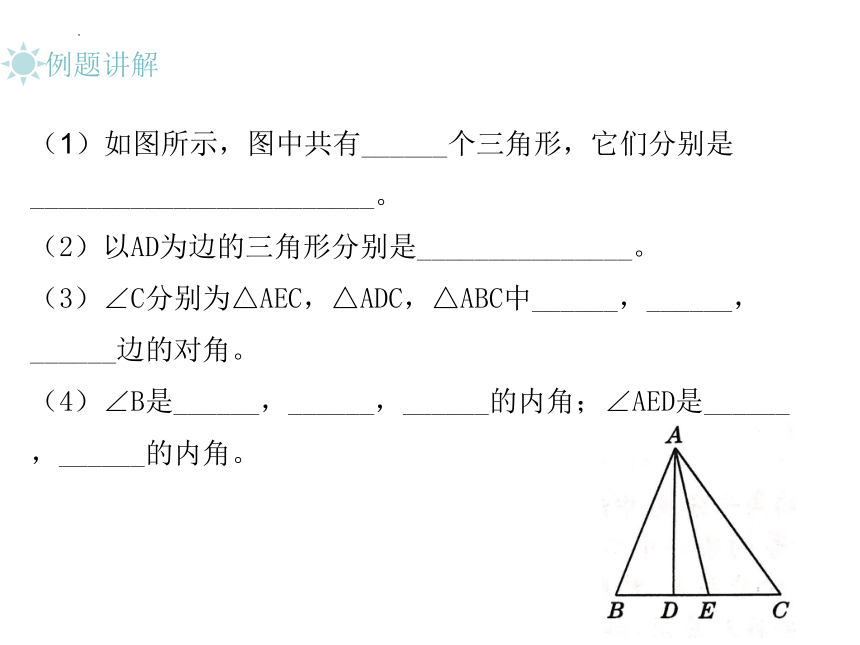
(1)如图所示,图中共有______个三角形,它们分别是________________________。
(2)以AD为边的三角形分别是_______________。
(3)∠C分别为△AEC,△ADC,△ABC中______,______,______边的对角。
(4)∠B是______,______,______的内角;∠AED是______,______的内角。
应用练习
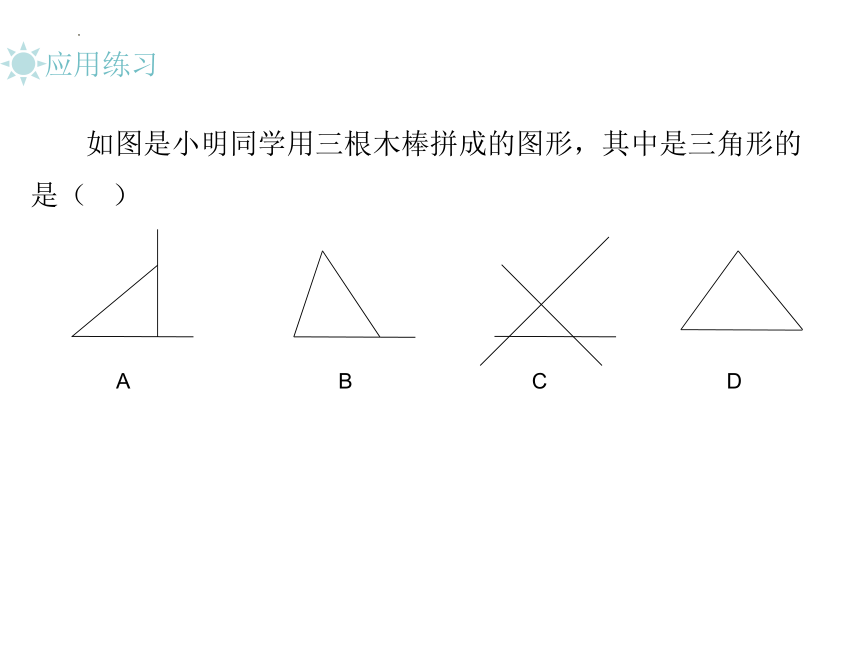
如图是小明同学用三根木棒拼成的图形,其中是三角形的是( )
A B C D
应用练习
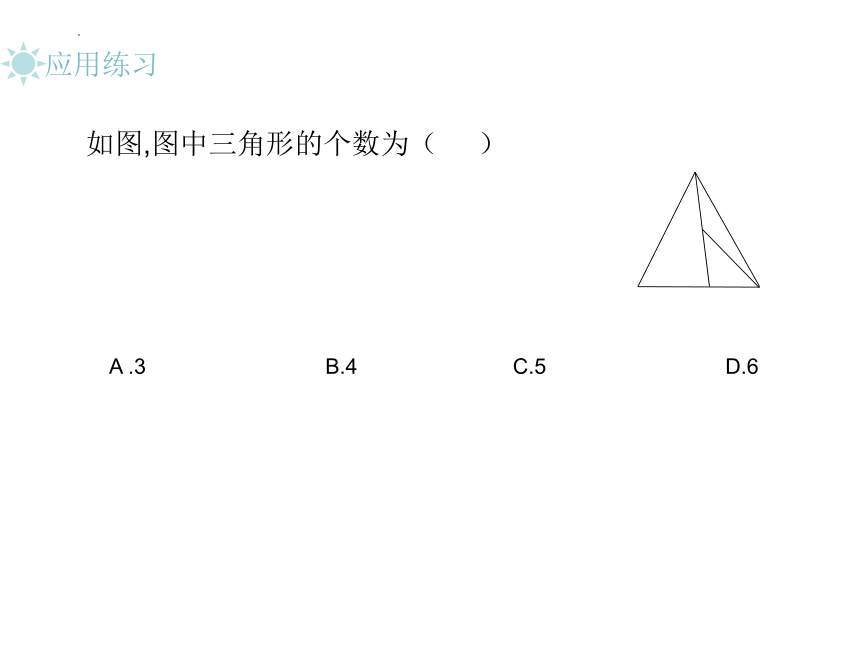
如图,图中三角形的个数为( )
A .3 B.4 C.5 D.6
知识点2 三角形的分类
三角形按角分类:可分为锐角三角形、直角三角形、钝角三角形。
锐角三角形:三个角都是锐角
直角三角形:有一个角是直角
钝角三角形:有一个角是钝角
实际上,这种分类和命名的方法是按照三角形中最大角来进行的,若最大角是钝角,则该三角形是钝角三角形。
例题讲解
已知在△ABC中,∠C=3(∠A+∠B),你能判断该三角形的形状吗?请说明理由。
应用练习
图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
知识点3 三角形的三边关系
三角形的三边有的各不相等,有的两边相等,有的三边相等,有两边相等的三角形叫做等腰三角形,如图所示。三边都相等的三角形是等边三角形。
知识点3 三角形的三边关系
(1)任意两边之和大于第三边。
(2)任意两边之差小于第三边。
用几何语言表示,如图所示,如果△ABC的三边长分别为a,b,c,则:
①a+b>c,a+c>b,b+c>a;
②I c-a I<b,I c-b I<a,I a-b I<c。
c
b
a
C
B
A
例题讲解
下列各组线段中,能构成三角形的是( )
A.a=6,b=8,c=15
B.a=7,b=6,c=13
C.a=4,b=5,c=6
D.a=12,b=14,c=18
?
应用练习
三角形按边可分为( )
A.等腰三角形、直角三角形、锐角三角形
B.直角三角形、不等边三角形
C.等腰三角形、不等边三角形
D.等腰三角形、等边三角形
应用练习
下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4 B.5,7,7 C.5,6,12 D.6,8,10
应用练习
长度为2cm,3cm,4cm和5cm的4根木棒,从中任取三根,可搭成( )种不同的三角形。
应用练习
已知一个三角形两边的长分别是2和3,若它的第三边长为奇数,则这个三角形的周长为______。
应用练习
已知三角形的三边长????,????,????满足(?????????)2+?????????=0,
则△ABC的形状是( )
A.钝角三角形 B.直角三角形
C.等边三角形 D.以上都不对
?
应用练习
一个三角形两边的长分别为3和7,且第三边的长为整数,这样的三角形的周长的最小值是( )
A.14 B.15 C.16 D.17
应用练习
若一个等腰三角形的周长为18cm,一边长为7cm,则其他两边的长为________。
应用练习
已知????,????,????是一个三角形的三边长,化简:
?????????+????+??????????????
学习目标
1.认识三角形的概念及三角形的基本要素。
2.理解三角形三条边之间的关系,会给三角形分类。
知识点1 三角形的概念
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形,三角形用符号“△”表示,读作“三角形”。
组成三角形的三条线段叫做三角形的边;相邻两边的公共端点叫做三角形的顶点;相邻两边的夹角叫做三角形的内角。
知识点1 三角形的概念
用数学语言描述如图所示的三角形,顶点是A,B,C的三角形记作△ABC,读作“三角形ABC”,三角形有三个顶点:A,B,C;有三条边:AB,BC,AC;有三个内角:∠A,∠B,∠C。
通常当△ABC的三边用a,b,c表示时,顶点A所对的边BC用a表示,顶点B所对的边AC用b表示,顶点C所对的边AB用c表示。
c
b
a
C
B
A
例题讲解
(1)如图所示,图中共有______个三角形,它们分别是________________________。
(2)以AD为边的三角形分别是_______________。
(3)∠C分别为△AEC,△ADC,△ABC中______,______,______边的对角。
(4)∠B是______,______,______的内角;∠AED是______,______的内角。
应用练习
如图是小明同学用三根木棒拼成的图形,其中是三角形的是( )
A B C D
应用练习
如图,图中三角形的个数为( )
A .3 B.4 C.5 D.6
知识点2 三角形的分类
三角形按角分类:可分为锐角三角形、直角三角形、钝角三角形。
锐角三角形:三个角都是锐角
直角三角形:有一个角是直角
钝角三角形:有一个角是钝角
实际上,这种分类和命名的方法是按照三角形中最大角来进行的,若最大角是钝角,则该三角形是钝角三角形。
例题讲解
已知在△ABC中,∠C=3(∠A+∠B),你能判断该三角形的形状吗?请说明理由。
应用练习
图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
知识点3 三角形的三边关系
三角形的三边有的各不相等,有的两边相等,有的三边相等,有两边相等的三角形叫做等腰三角形,如图所示。三边都相等的三角形是等边三角形。
知识点3 三角形的三边关系
(1)任意两边之和大于第三边。
(2)任意两边之差小于第三边。
用几何语言表示,如图所示,如果△ABC的三边长分别为a,b,c,则:
①a+b>c,a+c>b,b+c>a;
②I c-a I<b,I c-b I<a,I a-b I<c。
c
b
a
C
B
A
例题讲解
下列各组线段中,能构成三角形的是( )
A.a=6,b=8,c=15
B.a=7,b=6,c=13
C.a=4,b=5,c=6
D.a=12,b=14,c=18
?
应用练习
三角形按边可分为( )
A.等腰三角形、直角三角形、锐角三角形
B.直角三角形、不等边三角形
C.等腰三角形、不等边三角形
D.等腰三角形、等边三角形
应用练习
下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4 B.5,7,7 C.5,6,12 D.6,8,10
应用练习
长度为2cm,3cm,4cm和5cm的4根木棒,从中任取三根,可搭成( )种不同的三角形。
应用练习
已知一个三角形两边的长分别是2和3,若它的第三边长为奇数,则这个三角形的周长为______。
应用练习
已知三角形的三边长????,????,????满足(?????????)2+?????????=0,
则△ABC的形状是( )
A.钝角三角形 B.直角三角形
C.等边三角形 D.以上都不对
?
应用练习
一个三角形两边的长分别为3和7,且第三边的长为整数,这样的三角形的周长的最小值是( )
A.14 B.15 C.16 D.17
应用练习
若一个等腰三角形的周长为18cm,一边长为7cm,则其他两边的长为________。
应用练习
已知????,????,????是一个三角形的三边长,化简:
?????????+????+??????????????
