人教版八年级数学上册11.3多边形及其内角和 专题训练 (无答案)
文档属性
| 名称 | 人教版八年级数学上册11.3多边形及其内角和 专题训练 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 17:13:24 | ||
图片预览


文档简介
多边形及其内角和专题训练2023-2024学年人教版八年级数学上册
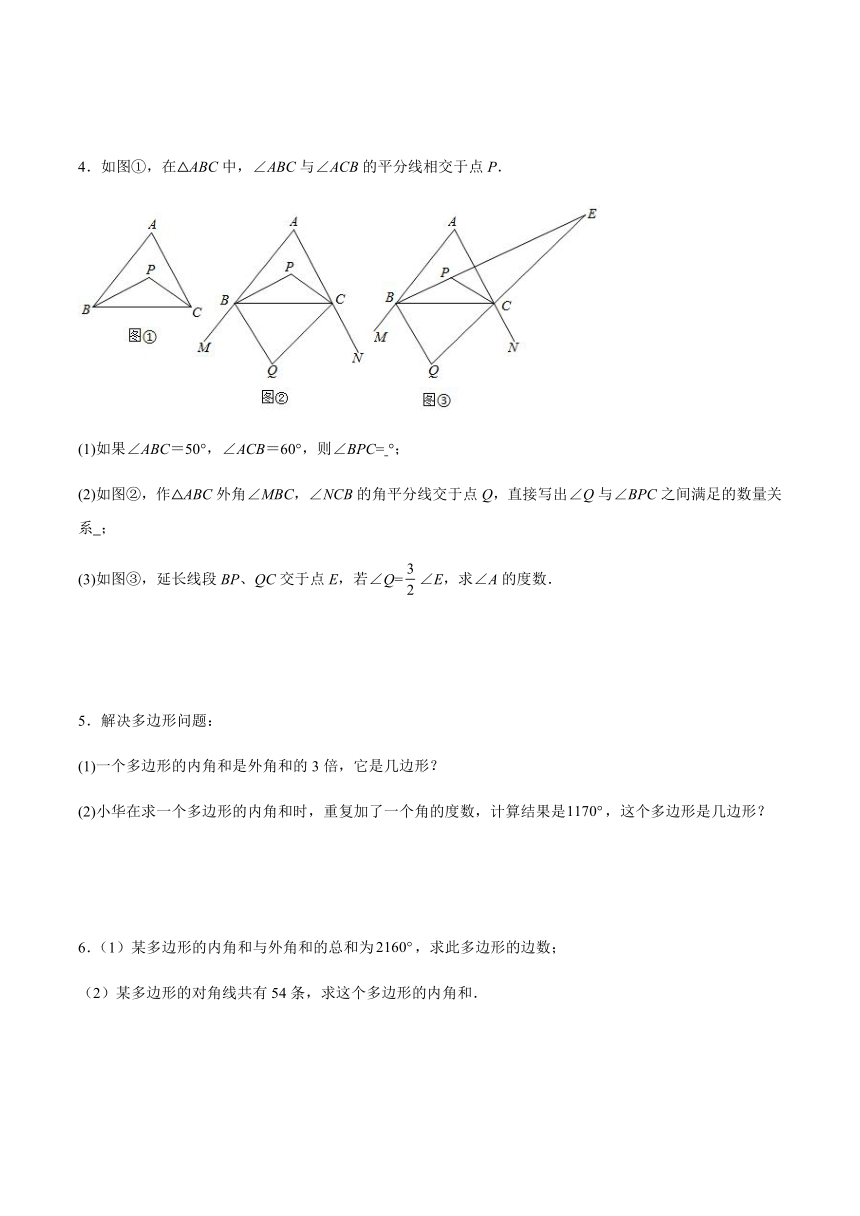
1.如图,阅读佳佳与明明的对话,解决下列问题:
(1)“多边形内角和为”可能吗?________;(选填“可能”或“不可能”)
(2)明明求的是几边形的内角和?
2.求下列各图中x的值.
3.如图,在四边形中,,与,相邻的外角都是.求的外角的度数.
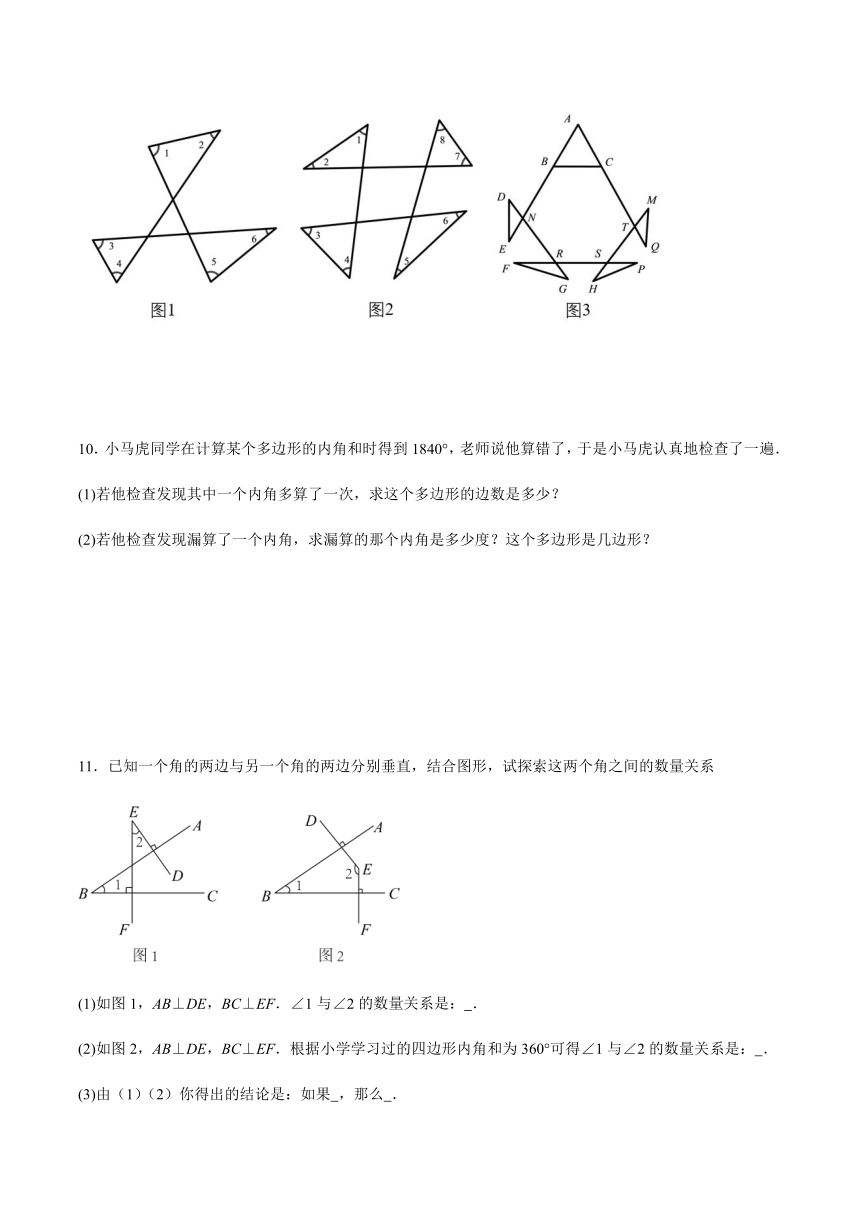
4.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠ABC=50°,∠ACB=60°,则∠BPC= °;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,直接写出∠Q与∠BPC之间满足的数量关系 ;
(3)如图③,延长线段BP、QC交于点E,若∠Q=∠E,求∠A的度数.
5.解决多边形问题:
(1)一个多边形的内角和是外角和的3倍,它是几边形?
(2)小华在求一个多边形的内角和时,重复加了一个角的度数,计算结果是,这个多边形是几边形?
6.(1)某多边形的内角和与外角和的总和为,求此多边形的边数;
(2)某多边形的对角线共有54条,求这个多边形的内角和.
7.已知一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的.
(1)求这个多边形每个外角的度数;
(2)求这个多边形的内角和.
8.已知如图1,线段AB,CD相交于O点,连接AD,CB,我们把如图1的图形称之为“8字形”.那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)在图1中,请写出∠A,∠B,∠C,∠D之间的数量关系,并说明理由;
(2)如图2,计算∠A+∠B+∠C+∠D+∠E+∠F的度数.
9.(1)如图1,则________;
(2)如图2,则________;
(3)如图3,则________.
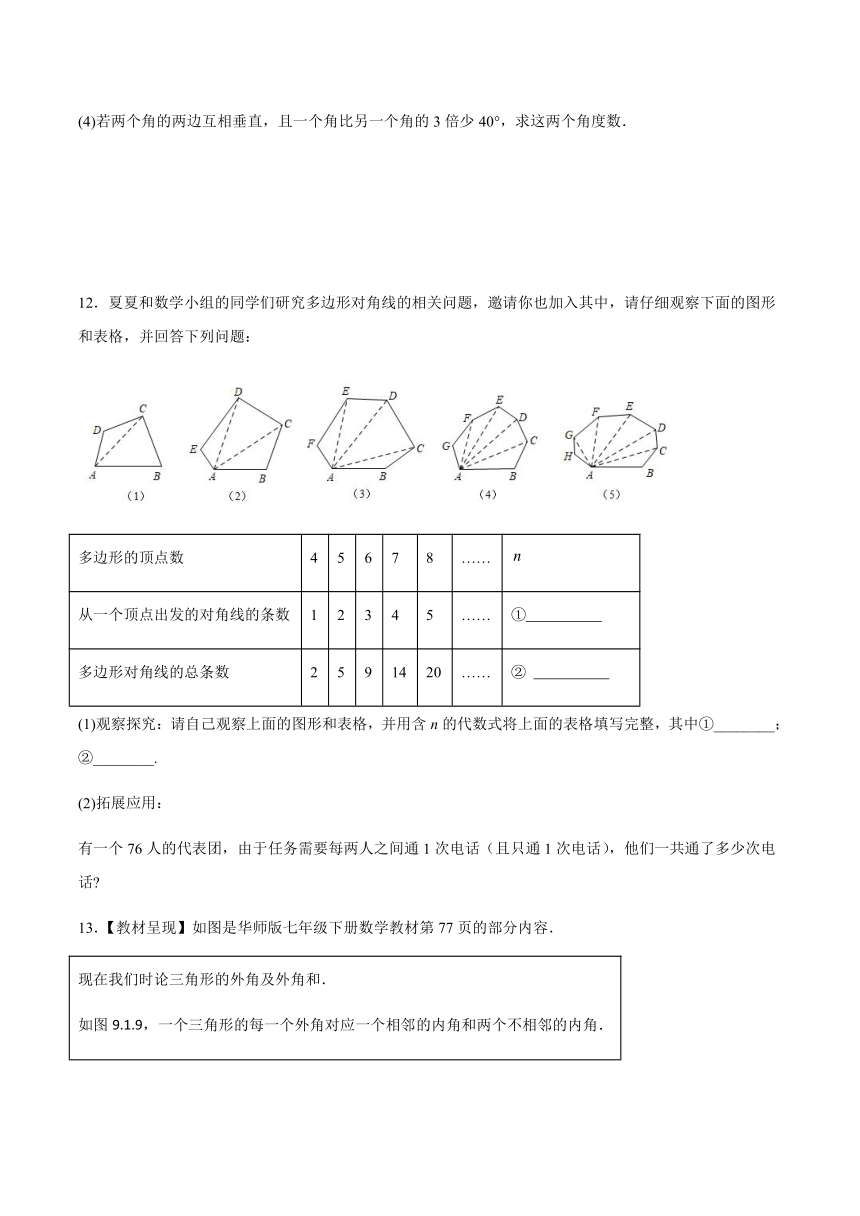
10.小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍.
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
11.已知一个角的两边与另一个角的两边分别垂直,结合图形,试探索这两个角之间的数量关系
(1)如图1,AB⊥DE,BC⊥EF.∠1与∠2的数量关系是: .
(2)如图2,AB⊥DE,BC⊥EF.根据小学学习过的四边形内角和为360°可得∠1与∠2的数量关系是: .
(3)由(1)(2)你得出的结论是:如果 ,那么 .
(4)若两个角的两边互相垂直,且一个角比另一个角的3倍少40°,求这两个角度数.
12.夏夏和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中,请仔细观察下面的图形和表格,并回答下列问题:
多边形的顶点数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 …… ①
多边形对角线的总条数 2 5 9 14 20 …… ②
(1)观察探究:请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①________;②________.
(2)拓展应用:
有一个76人的代表团,由于任务需要每两人之间通1次电话(且只通1次电话),他们一共通了多少次电话
13.【教材呈现】如图是华师版七年级下册数学教材第77页的部分内容.
现在我们时论三角形的外角及外角和. 如图9.1.9,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角. 三角形的外角写内角有什么关系呢? 在图9.1.10中,显然有 (外角)(相邻的内角) 那么外角与其他两个不相邻的内角又有什么关系呢? 依据三角形的内角和等于,我们有. 由上面两个式子,可以推出 . . 因而可以得到你与你的同伴所发现的结论: . 由此可知,三角形的外角有两条性质: 1.三角形的一个外角等于与它不相同的两个内角的和. 2.三角形的一个外角大于任何一个与它不相邻的内角.
【感知】如图①,在四边形中,分别是边的延长线,我们把、称为四边形的外角,若,则___________度.
【探究】如图②,在四边形中,分别是边的延长线,我们把、称为四边形的外角,试探究与之间的数量关系,并说明理由.
【应用】如图③,、分别是四边形的外角的平分线,若,则的度数为______________________.
14.如图:已知,与的角平分线相交于点F.
(1)如图1,若,求的度数;
(2)如图2,若,分别平分与,写出与之间的数量关系,并说明理由;
(3)若,,设,直接写出用含m,n的代数式表示________.
15.利用“模型”解决几何综合问题往往会取得事半功倍的效果.
几何模型:如图(1),我们称它为“A”型图案,
易证明:∠EDF = ∠A + ∠B + ∠C;
应用上面模型解决问题:
(1)如图(2),“五角星”形,求?
分析: 图中是“A”型图,于是,
所以= ;
(2)如图(3),“七角星”形,求;
(3)如图(4),“八角星”形,可以求得= ;
16.如图1,我们分别研究过三角形中两内角平分线所成的、两外角平分线所成的、一内角一外角平分线所成的与的关系.
(1)如图2,在四边形中,、分别平分和,则与,的数量关系为 .
(2)如图3,在四边形中,、分别平分和,请探究与,的数量关系,并说明理由.
(3)在四边形中,为的平分线与边和延长线所成角的平分线所在的直线构成的锐角,若设,,则 .(用α、β表示)
17.如图1,点M,N分别在正五边形ABCDE的边BC,CD上,BM=CN,连结AM,BN相交于H.
(1)求正五边形ABCDE外角的度数;
(2)求∠AHB的度数;
(3)如图2,将条件中的“正五边形ABCDE”换成“正六边形ABCDEF”,其他条件不变,试猜想∠AHB的度数.
18.已知:多边形的外角和的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图①,,BM与DN交于点P,求的度数;
②如图②,猜测当和满足什么数量关系时,,并证明你的猜想.
如图③,若多边形是五边形ABCDG,已知,BM与DN交于点P,求的度数.
19.如图,中,的角平分线与外角的平分线交于.
(1)如图1,若,则 .
(2)如图2,四边形中,的角平分线及外角的角平分线相交于点F,若,求的度数.
(3)如图3,中,的角平分线与外角的角平分线交于,若E为延长线上一动点,连接与的角平分线交于点Q,当E滑动时有下面两个结论:
①的值为定值;
②的值为定值;
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
20.阅读下题及解题过程.
如图(),我们知道四边形的内角和为,现在将一张四边形的纸剪掉一个角后,剩余纸所有内角的和是多少?
如图(),剩余纸为五边形,所以剩余纸所有内角的和为.
上面的解答过程是否正确?若正确,说出你的判断根据;若不正确,请说明原因,并写出你认为正确的结论.
21.探究归纳题:
(1)试验分析:
如图1,经过一个顶点(如点)可以作___________条对角线,它把四边形分为___________个三角形;
(2)拓展延伸:
运用(1)的分析方法,可得:图2过一个顶点作所有的对角线,把这个多边形分为___________个三角形;图3过一个顶点作所有的对角线,把这个多边形分为___________个三角形;
(3)探索归纳:对于边形,过一个顶点的所有对角线把这个边形分为___________个三角形.(用含的式子表示)
(4)特例验证:过一个顶点的所有对角线可把十边形分为___________个三角形.
1.如图,阅读佳佳与明明的对话,解决下列问题:
(1)“多边形内角和为”可能吗?________;(选填“可能”或“不可能”)
(2)明明求的是几边形的内角和?
2.求下列各图中x的值.
3.如图,在四边形中,,与,相邻的外角都是.求的外角的度数.
4.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠ABC=50°,∠ACB=60°,则∠BPC= °;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,直接写出∠Q与∠BPC之间满足的数量关系 ;
(3)如图③,延长线段BP、QC交于点E,若∠Q=∠E,求∠A的度数.
5.解决多边形问题:
(1)一个多边形的内角和是外角和的3倍,它是几边形?
(2)小华在求一个多边形的内角和时,重复加了一个角的度数,计算结果是,这个多边形是几边形?
6.(1)某多边形的内角和与外角和的总和为,求此多边形的边数;
(2)某多边形的对角线共有54条,求这个多边形的内角和.
7.已知一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的.
(1)求这个多边形每个外角的度数;
(2)求这个多边形的内角和.
8.已知如图1,线段AB,CD相交于O点,连接AD,CB,我们把如图1的图形称之为“8字形”.那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)在图1中,请写出∠A,∠B,∠C,∠D之间的数量关系,并说明理由;
(2)如图2,计算∠A+∠B+∠C+∠D+∠E+∠F的度数.
9.(1)如图1,则________;
(2)如图2,则________;
(3)如图3,则________.
10.小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍.
(1)若他检查发现其中一个内角多算了一次,求这个多边形的边数是多少?
(2)若他检查发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
11.已知一个角的两边与另一个角的两边分别垂直,结合图形,试探索这两个角之间的数量关系
(1)如图1,AB⊥DE,BC⊥EF.∠1与∠2的数量关系是: .
(2)如图2,AB⊥DE,BC⊥EF.根据小学学习过的四边形内角和为360°可得∠1与∠2的数量关系是: .
(3)由(1)(2)你得出的结论是:如果 ,那么 .
(4)若两个角的两边互相垂直,且一个角比另一个角的3倍少40°,求这两个角度数.
12.夏夏和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中,请仔细观察下面的图形和表格,并回答下列问题:
多边形的顶点数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 …… ①
多边形对角线的总条数 2 5 9 14 20 …… ②
(1)观察探究:请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①________;②________.
(2)拓展应用:
有一个76人的代表团,由于任务需要每两人之间通1次电话(且只通1次电话),他们一共通了多少次电话
13.【教材呈现】如图是华师版七年级下册数学教材第77页的部分内容.
现在我们时论三角形的外角及外角和. 如图9.1.9,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角. 三角形的外角写内角有什么关系呢? 在图9.1.10中,显然有 (外角)(相邻的内角) 那么外角与其他两个不相邻的内角又有什么关系呢? 依据三角形的内角和等于,我们有. 由上面两个式子,可以推出 . . 因而可以得到你与你的同伴所发现的结论: . 由此可知,三角形的外角有两条性质: 1.三角形的一个外角等于与它不相同的两个内角的和. 2.三角形的一个外角大于任何一个与它不相邻的内角.
【感知】如图①,在四边形中,分别是边的延长线,我们把、称为四边形的外角,若,则___________度.
【探究】如图②,在四边形中,分别是边的延长线,我们把、称为四边形的外角,试探究与之间的数量关系,并说明理由.
【应用】如图③,、分别是四边形的外角的平分线,若,则的度数为______________________.
14.如图:已知,与的角平分线相交于点F.
(1)如图1,若,求的度数;
(2)如图2,若,分别平分与,写出与之间的数量关系,并说明理由;
(3)若,,设,直接写出用含m,n的代数式表示________.
15.利用“模型”解决几何综合问题往往会取得事半功倍的效果.
几何模型:如图(1),我们称它为“A”型图案,
易证明:∠EDF = ∠A + ∠B + ∠C;
应用上面模型解决问题:
(1)如图(2),“五角星”形,求?
分析: 图中是“A”型图,于是,
所以= ;
(2)如图(3),“七角星”形,求;
(3)如图(4),“八角星”形,可以求得= ;
16.如图1,我们分别研究过三角形中两内角平分线所成的、两外角平分线所成的、一内角一外角平分线所成的与的关系.
(1)如图2,在四边形中,、分别平分和,则与,的数量关系为 .
(2)如图3,在四边形中,、分别平分和,请探究与,的数量关系,并说明理由.
(3)在四边形中,为的平分线与边和延长线所成角的平分线所在的直线构成的锐角,若设,,则 .(用α、β表示)
17.如图1,点M,N分别在正五边形ABCDE的边BC,CD上,BM=CN,连结AM,BN相交于H.
(1)求正五边形ABCDE外角的度数;
(2)求∠AHB的度数;
(3)如图2,将条件中的“正五边形ABCDE”换成“正六边形ABCDEF”,其他条件不变,试猜想∠AHB的度数.
18.已知:多边形的外角和的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图①,,BM与DN交于点P,求的度数;
②如图②,猜测当和满足什么数量关系时,,并证明你的猜想.
如图③,若多边形是五边形ABCDG,已知,BM与DN交于点P,求的度数.
19.如图,中,的角平分线与外角的平分线交于.
(1)如图1,若,则 .
(2)如图2,四边形中,的角平分线及外角的角平分线相交于点F,若,求的度数.
(3)如图3,中,的角平分线与外角的角平分线交于,若E为延长线上一动点,连接与的角平分线交于点Q,当E滑动时有下面两个结论:
①的值为定值;
②的值为定值;
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
20.阅读下题及解题过程.
如图(),我们知道四边形的内角和为,现在将一张四边形的纸剪掉一个角后,剩余纸所有内角的和是多少?
如图(),剩余纸为五边形,所以剩余纸所有内角的和为.
上面的解答过程是否正确?若正确,说出你的判断根据;若不正确,请说明原因,并写出你认为正确的结论.
21.探究归纳题:
(1)试验分析:
如图1,经过一个顶点(如点)可以作___________条对角线,它把四边形分为___________个三角形;
(2)拓展延伸:
运用(1)的分析方法,可得:图2过一个顶点作所有的对角线,把这个多边形分为___________个三角形;图3过一个顶点作所有的对角线,把这个多边形分为___________个三角形;
(3)探索归纳:对于边形,过一个顶点的所有对角线把这个边形分为___________个三角形.(用含的式子表示)
(4)特例验证:过一个顶点的所有对角线可把十边形分为___________个三角形.
