《有理数》全章复习与巩固(提高)知识讲解
文档属性
| 名称 | 《有理数》全章复习与巩固(提高)知识讲解 | 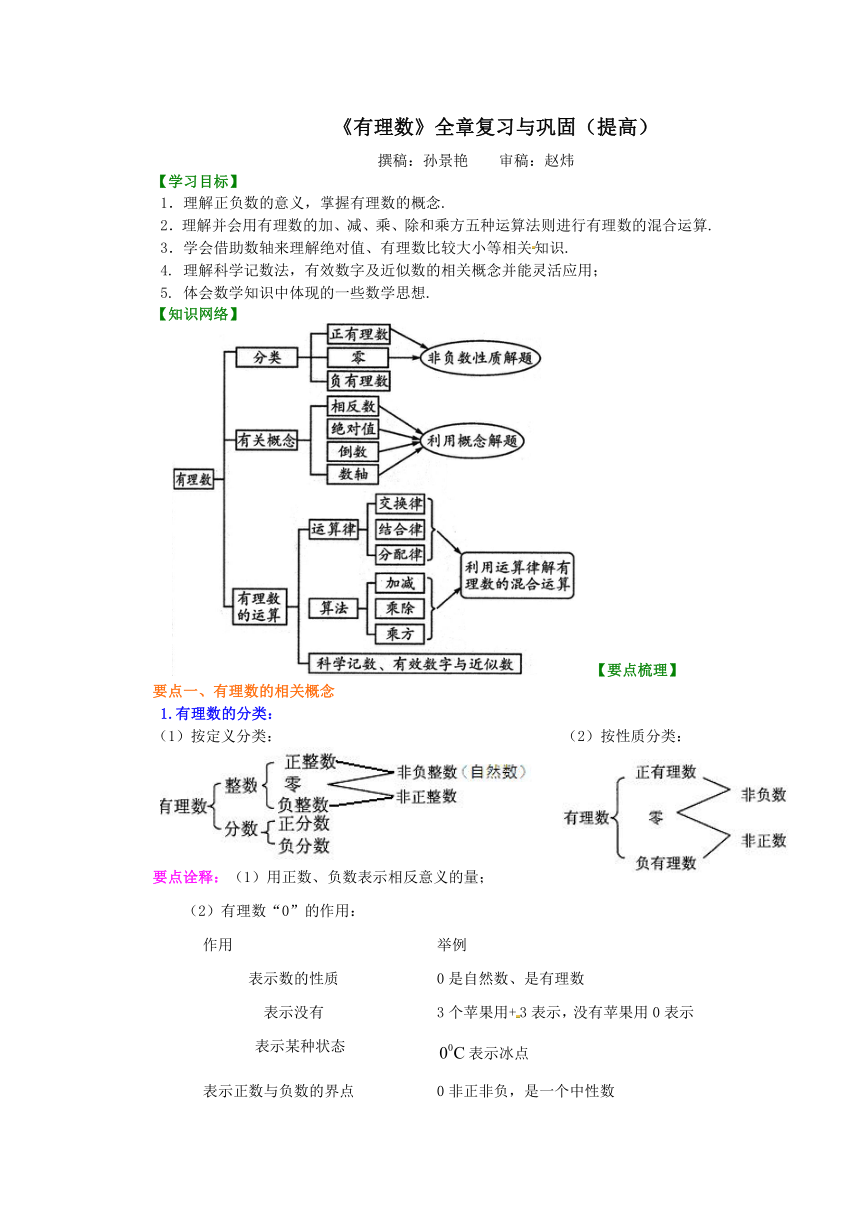 | |
| 格式 | zip | ||
| 文件大小 | 260.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-27 20:43:33 | ||
图片预览




文档简介
《有理数》全章复习与巩固(提高)
撰稿:孙景艳 审稿:赵炜
【学习目标】
1.理解正负数的意义,掌握有理数的概念.
2.理解并会用有理数的加、减、乘、除和乘方五种运算法则进行有理数的混合运算.
3.学会借助数轴来理解绝对值、有理数比较大小等相关知识.
4. 理解科学记数法,有效数字及近似数的相关概念并能灵活应用;
5. 体会数学知识中体现的一些数学思想.
【知识网络】
【要点梳理】
要点一、有理数的相关概念
1.有理数的分类:
(1)按定义分类: (2)按性质分类:
要点诠释:(1)用正数、负数表示相反意义的量;
(2)有理数“0”的作用:
作用 举例
表示数的性质 0是自然数、是有理数
表示没有 3个苹果用+3表示,没有苹果用0表示
表示某种状态 表示冰点
表示正数与负数的界点 0非正非负,是一个中性数
2.数轴:规定了原点、正方向和单位长度的直线.
要点诠释:(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.
(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.
3.相反数:只有符号不同的两个数互称为相反数,0的相反数是0.
要点诠释:(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“”号即可.
(3)多重符号的化简:数字前面“”号的个数若有偶数个时,化简结果为正,若有奇数个时,化简结果为负.
4.绝对值:
(1)代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
数a的绝对值记作.
(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.
要点二、有理数的运算
1.法则
(1)加法法则:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.③一个数同0相加,仍得这个数.
(2)减法法则:减去一个数,等于加这个数的相反数.即a-b=a+(-b)
(3)乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘.②任何数同0相乘,都得0.
(4)除法法则:除以一个不等于0的数,等于乘这个数的倒数.即a÷b=a·(b≠0)
(5)乘方运算的符号法则:①负数的奇次幂是负数,负数的偶次幂是正数;②正数的任何次幂都是正数,0的任何非零次幂都是0,
(6)有理数的混合运算顺序:①先乘方,再乘除,最后加减;②同级运算,从左到右进行;
③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
要点诠释:“奇负偶正”口诀的应用:
(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,
-[+(-3)]=3.
(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是负因数的个数,正负指结果中积的符号,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.
(3)有理数乘方,这里奇偶指的是指数,当底数为负数时,指数为奇数,则幂为负;指数为偶数,则幂为正,例如:, .
2.运算律 :
(1)交换律: ① 加法交换律:a+b=b+a; ②乘法交换律:ab=ba;
(2)结合律: ①加法结合律: (a+b)+c=a+(b+c); ②乘法结合律:(ab)c=a(bc)
(3)分配律:a(b+c)=ab+ac
要点三、有理数的大小比较
比较大小常用的方法有:(1)数轴比较法;(2)法则比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3) 作差比较法.(4)作商比较法;(5)倒数比较法.
要点四、科学记数法
1. 科学记数法:把一个大于10的数表示成的形式(其中,是正整数),此种记法叫做科学记数法.例如:200 000=.
2.有效数字:从一个数的左边第一个非0数字起,到末位数字止,所有数字都是这个数的有效数字. 如:0.000 27有两个有效数字:2,7.
注意:万=,亿=10
【典型例题】
类型一、有理数相关概念
1. 已知x与y互为相反数,m与n互为倒数,|x+y |+(a-1)2=0,求a2-(x+y+mn)a+(x+y)2009+(-mn)2010的值.
【思路点拨】(1)若有理数x与y互为相反数,则x+y=0,反过来也成立.
(2)若有理数m与n互为倒数,则mn=1,反过来也成立.
【答案与解析】因为x与y互为相反数,m与n互为倒数,(a-1)2≥0,
所以x+y=0,mn=1,a=1,
所以a2-(x+y+mn)a+(x+y)2009+(-mn)2010
=a2-(0+1)a+02009+(-1)2010
=a2-a+1.
∵a=1,∴原式=12-1+1=1
【总结升华】要全面正确地理解倒数,绝对值,相反数等概念.
举一反三:
【高清课堂:有理数的复习与提高 357129 复习例题2】
【变式1】选择题
(1)已知四种说法:
①|a|=a时,a>0; |a|=-a时, a<0. ②|a|就是a与-a中较大的数.
③|a|就是数轴上a到原点的距离. ④对于任意有理数,-|a|≤a≤|a|.
其中说法正确的个数是( )
A.1 B.2 C.3 D.4
(2)有四个说法:
①有最小的有理数 ②有绝对值最小的有理数
③有最小的正有理数 ④没有最大的负有理数
上述说法正确的是( )
A.①② B.③④ C.②④ D.①②
(3)已知(-ab)3>0,则( )
A.ab<0 B.ab>0 C.a>0且b<0 D.a<0且b<0
(4)若|x-1|+|y+3|+|z-5|=0,则(x+1)(y-3)(z+5)的值是( )
A.120 B.-15 C.0 D.-120
(5)下列各对算式中,结果相等的是( )
A.-a6与(-a)6 B.-a3与|-a|3 C.[(-a)2]3与(-a3)2 D.(ab)3与ab3
【答案】(1)C;(2)C;(3)A;(4)D;(5)C
【变式2】某市2008年的国民生产总值约为333.9亿元,预计2009年比上一年增长10%,表示2009年这个市的国民生产总值应是(结果保留3个有效数字)________元.
【答案】. 提示:(亿元)(元)
2. 在下列两数之间填上适当的不等号:
________.
【思路点拨】在a、b均为正数的条件下,根据“,,分别得到a>b,a=b,a<b”来比较两数的大小.
【答案】 >
【解析】法一:作差法:()
=,
∴.
法二:作商法:由于,所以.
再根据两个负数,绝对值大的反而小,得到:.
【总结升华】比较大小常用的有五种方法,要根据数的特征选择使用.
举一反三:
【变式】在下列两数之间填上适当的不等号.
_________.
【答案】> (提示:倒数法较简便)
类型二、有理数的运算
【高清课堂:有理数专题复习 357133 有理数的混合运算】
3. (1)
(2)
(4)
(5)
【答案与解析】(1)原式
(2)原式
(3)原式
(4)原式
(5)
【总结升华】有理数的混合运算有很多技巧,如:正、负数分别相加;分数中,同分母或分母有倍数关系的分数结合相加;除法转化为乘法、正向应用乘法分配律:a(b+c)=ab+ac;逆向应用分配律:ab+ac=a(b+c)等.
举一反三:
【变式】
(1)
(2)
【答案】
(1)
(2)
4. 先观察下列各式:;;
;…;,根据以上观察,计算:
…的值.
【答案与解析】原式
.
【总结升华】根据题中提供的拆项方法把每一项拆成的形式,然后再进行计算.
举一反三:
【高清课堂:有理数的复习与提高 例2】
【变式】用简单方法计算:
【答案】原式
=
类型三、数学思想在本章中的应用
5.(1)数形结合思想:已知有理数a、b在数轴上对应点的位置如图所示,且|a|>|b|,求|a|-|a+b|-|b-a|的值.
A.2b+a B.2b-a C.a D.b
(2)分类讨论思想:已知a是任一有理数,试比较|a|与-2a的大小.
(3)转化思想:.
【答案与解析】(1)从数轴上a、b两点的位置可以看出a<0,b>0,且|a|>|b|,所以|a|-|a+b|-|b-a|=-a+a+b-b+a=a.
(2)a可能是正数,0或负数,这就需要分类讨论:
当a>0时,|a|=a>0,-2a<0,所以|a|>-2a;
当a=0时,|a|=0,-2a=0,所以|a|=-2a;
当a<0时,|a|=-a>0,-2a>0,又-a<-2a,所以|a|<-2a.
综上所述:当a≥0时, |a|≥-2a;当a<0时,|a|<-2a.
(3).
【总结升华】在解题中合理利用数学思想,是解决问题的有效手段.数形结合——“以形助数”或“以数解形”使问题简单化,具体化;分类讨论中注意分类的两条原则:分类标准要统一,而且分类要做到不重不漏;转化思想就是把“新知识”转化为“旧知识”,将“未知”转化为“已知”.
类型四、规律探索
6. (安徽)下面两个多位数1248624…,6248624…都是按照如下方法得到的:将第1位数字乘以2,若积为一位数,将其写在第2位;若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( ).
A.495 B.497 C.501 D.503
【思路点拨】多位数1248624…是怎么来的?当第1个数字是1时,将第1位数字乘以2得2,将2写在第2位上,再将第2位数字2乘以2得4,将其写在第3位上,将第3位数字4乘以2的8,将8写在第4位上,将第4位数字8乘以2得16,将16的个位数字6写在第5位上,将第5位数字6乘以2得12,将12的个位数字2写在第6位上,再将第6位数字2乘以2得4,将其写在第7位上,以此类推.根据此方法可得到第一位是3的多位数后再求和.
【答案】A
【解析】按照法则可以看出此数为362 486 248…,后面6248循环,所以前100位的所有数字之和是3+(6+2+4+8)×24+6+2+4=495,所以选A.
【总结升华】特例助思,探究规律,这类题主要是通过观察分析,从特殊到一般来总结发现规律,并表示出来.
举一反三:
【变式】(2009·山东聊城)将1,,,,,,…,按一定规律排列如下:
请你写出第20行从左至右第10个数是________.
【答案】
撰稿:孙景艳 审稿:赵炜
【学习目标】
1.理解正负数的意义,掌握有理数的概念.
2.理解并会用有理数的加、减、乘、除和乘方五种运算法则进行有理数的混合运算.
3.学会借助数轴来理解绝对值、有理数比较大小等相关知识.
4. 理解科学记数法,有效数字及近似数的相关概念并能灵活应用;
5. 体会数学知识中体现的一些数学思想.
【知识网络】
【要点梳理】
要点一、有理数的相关概念
1.有理数的分类:
(1)按定义分类: (2)按性质分类:
要点诠释:(1)用正数、负数表示相反意义的量;
(2)有理数“0”的作用:
作用 举例
表示数的性质 0是自然数、是有理数
表示没有 3个苹果用+3表示,没有苹果用0表示
表示某种状态 表示冰点
表示正数与负数的界点 0非正非负,是一个中性数
2.数轴:规定了原点、正方向和单位长度的直线.
要点诠释:(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.
(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.
3.相反数:只有符号不同的两个数互称为相反数,0的相反数是0.
要点诠释:(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“”号即可.
(3)多重符号的化简:数字前面“”号的个数若有偶数个时,化简结果为正,若有奇数个时,化简结果为负.
4.绝对值:
(1)代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
数a的绝对值记作.
(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.
要点二、有理数的运算
1.法则
(1)加法法则:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.③一个数同0相加,仍得这个数.
(2)减法法则:减去一个数,等于加这个数的相反数.即a-b=a+(-b)
(3)乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘.②任何数同0相乘,都得0.
(4)除法法则:除以一个不等于0的数,等于乘这个数的倒数.即a÷b=a·(b≠0)
(5)乘方运算的符号法则:①负数的奇次幂是负数,负数的偶次幂是正数;②正数的任何次幂都是正数,0的任何非零次幂都是0,
(6)有理数的混合运算顺序:①先乘方,再乘除,最后加减;②同级运算,从左到右进行;
③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
要点诠释:“奇负偶正”口诀的应用:
(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,
-[+(-3)]=3.
(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是负因数的个数,正负指结果中积的符号,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.
(3)有理数乘方,这里奇偶指的是指数,当底数为负数时,指数为奇数,则幂为负;指数为偶数,则幂为正,例如:, .
2.运算律 :
(1)交换律: ① 加法交换律:a+b=b+a; ②乘法交换律:ab=ba;
(2)结合律: ①加法结合律: (a+b)+c=a+(b+c); ②乘法结合律:(ab)c=a(bc)
(3)分配律:a(b+c)=ab+ac
要点三、有理数的大小比较
比较大小常用的方法有:(1)数轴比较法;(2)法则比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3) 作差比较法.(4)作商比较法;(5)倒数比较法.
要点四、科学记数法
1. 科学记数法:把一个大于10的数表示成的形式(其中,是正整数),此种记法叫做科学记数法.例如:200 000=.
2.有效数字:从一个数的左边第一个非0数字起,到末位数字止,所有数字都是这个数的有效数字. 如:0.000 27有两个有效数字:2,7.
注意:万=,亿=10
【典型例题】
类型一、有理数相关概念
1. 已知x与y互为相反数,m与n互为倒数,|x+y |+(a-1)2=0,求a2-(x+y+mn)a+(x+y)2009+(-mn)2010的值.
【思路点拨】(1)若有理数x与y互为相反数,则x+y=0,反过来也成立.
(2)若有理数m与n互为倒数,则mn=1,反过来也成立.
【答案与解析】因为x与y互为相反数,m与n互为倒数,(a-1)2≥0,
所以x+y=0,mn=1,a=1,
所以a2-(x+y+mn)a+(x+y)2009+(-mn)2010
=a2-(0+1)a+02009+(-1)2010
=a2-a+1.
∵a=1,∴原式=12-1+1=1
【总结升华】要全面正确地理解倒数,绝对值,相反数等概念.
举一反三:
【高清课堂:有理数的复习与提高 357129 复习例题2】
【变式1】选择题
(1)已知四种说法:
①|a|=a时,a>0; |a|=-a时, a<0. ②|a|就是a与-a中较大的数.
③|a|就是数轴上a到原点的距离. ④对于任意有理数,-|a|≤a≤|a|.
其中说法正确的个数是( )
A.1 B.2 C.3 D.4
(2)有四个说法:
①有最小的有理数 ②有绝对值最小的有理数
③有最小的正有理数 ④没有最大的负有理数
上述说法正确的是( )
A.①② B.③④ C.②④ D.①②
(3)已知(-ab)3>0,则( )
A.ab<0 B.ab>0 C.a>0且b<0 D.a<0且b<0
(4)若|x-1|+|y+3|+|z-5|=0,则(x+1)(y-3)(z+5)的值是( )
A.120 B.-15 C.0 D.-120
(5)下列各对算式中,结果相等的是( )
A.-a6与(-a)6 B.-a3与|-a|3 C.[(-a)2]3与(-a3)2 D.(ab)3与ab3
【答案】(1)C;(2)C;(3)A;(4)D;(5)C
【变式2】某市2008年的国民生产总值约为333.9亿元,预计2009年比上一年增长10%,表示2009年这个市的国民生产总值应是(结果保留3个有效数字)________元.
【答案】. 提示:(亿元)(元)
2. 在下列两数之间填上适当的不等号:
________.
【思路点拨】在a、b均为正数的条件下,根据“,,分别得到a>b,a=b,a<b”来比较两数的大小.
【答案】 >
【解析】法一:作差法:()
=,
∴.
法二:作商法:由于,所以.
再根据两个负数,绝对值大的反而小,得到:.
【总结升华】比较大小常用的有五种方法,要根据数的特征选择使用.
举一反三:
【变式】在下列两数之间填上适当的不等号.
_________.
【答案】> (提示:倒数法较简便)
类型二、有理数的运算
【高清课堂:有理数专题复习 357133 有理数的混合运算】
3. (1)
(2)
(4)
(5)
【答案与解析】(1)原式
(2)原式
(3)原式
(4)原式
(5)
【总结升华】有理数的混合运算有很多技巧,如:正、负数分别相加;分数中,同分母或分母有倍数关系的分数结合相加;除法转化为乘法、正向应用乘法分配律:a(b+c)=ab+ac;逆向应用分配律:ab+ac=a(b+c)等.
举一反三:
【变式】
(1)
(2)
【答案】
(1)
(2)
4. 先观察下列各式:;;
;…;,根据以上观察,计算:
…的值.
【答案与解析】原式
.
【总结升华】根据题中提供的拆项方法把每一项拆成的形式,然后再进行计算.
举一反三:
【高清课堂:有理数的复习与提高 例2】
【变式】用简单方法计算:
【答案】原式
=
类型三、数学思想在本章中的应用
5.(1)数形结合思想:已知有理数a、b在数轴上对应点的位置如图所示,且|a|>|b|,求|a|-|a+b|-|b-a|的值.
A.2b+a B.2b-a C.a D.b
(2)分类讨论思想:已知a是任一有理数,试比较|a|与-2a的大小.
(3)转化思想:.
【答案与解析】(1)从数轴上a、b两点的位置可以看出a<0,b>0,且|a|>|b|,所以|a|-|a+b|-|b-a|=-a+a+b-b+a=a.
(2)a可能是正数,0或负数,这就需要分类讨论:
当a>0时,|a|=a>0,-2a<0,所以|a|>-2a;
当a=0时,|a|=0,-2a=0,所以|a|=-2a;
当a<0时,|a|=-a>0,-2a>0,又-a<-2a,所以|a|<-2a.
综上所述:当a≥0时, |a|≥-2a;当a<0时,|a|<-2a.
(3).
【总结升华】在解题中合理利用数学思想,是解决问题的有效手段.数形结合——“以形助数”或“以数解形”使问题简单化,具体化;分类讨论中注意分类的两条原则:分类标准要统一,而且分类要做到不重不漏;转化思想就是把“新知识”转化为“旧知识”,将“未知”转化为“已知”.
类型四、规律探索
6. (安徽)下面两个多位数1248624…,6248624…都是按照如下方法得到的:将第1位数字乘以2,若积为一位数,将其写在第2位;若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( ).
A.495 B.497 C.501 D.503
【思路点拨】多位数1248624…是怎么来的?当第1个数字是1时,将第1位数字乘以2得2,将2写在第2位上,再将第2位数字2乘以2得4,将其写在第3位上,将第3位数字4乘以2的8,将8写在第4位上,将第4位数字8乘以2得16,将16的个位数字6写在第5位上,将第5位数字6乘以2得12,将12的个位数字2写在第6位上,再将第6位数字2乘以2得4,将其写在第7位上,以此类推.根据此方法可得到第一位是3的多位数后再求和.
【答案】A
【解析】按照法则可以看出此数为362 486 248…,后面6248循环,所以前100位的所有数字之和是3+(6+2+4+8)×24+6+2+4=495,所以选A.
【总结升华】特例助思,探究规律,这类题主要是通过观察分析,从特殊到一般来总结发现规律,并表示出来.
举一反三:
【变式】(2009·山东聊城)将1,,,,,,…,按一定规律排列如下:
请你写出第20行从左至右第10个数是________.
【答案】
