28.2 解直角三角形及其应用(课时2)同步练习 人教版数学九年级下册(含解析)
文档属性
| 名称 | 28.2 解直角三角形及其应用(课时2)同步练习 人教版数学九年级下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 17:15:04 | ||
图片预览


文档简介
《28.2 解直角三角形及其应用》同步练习
(课时2 应用举例(1))
一、基础巩固
知识点1 一般的实际问题
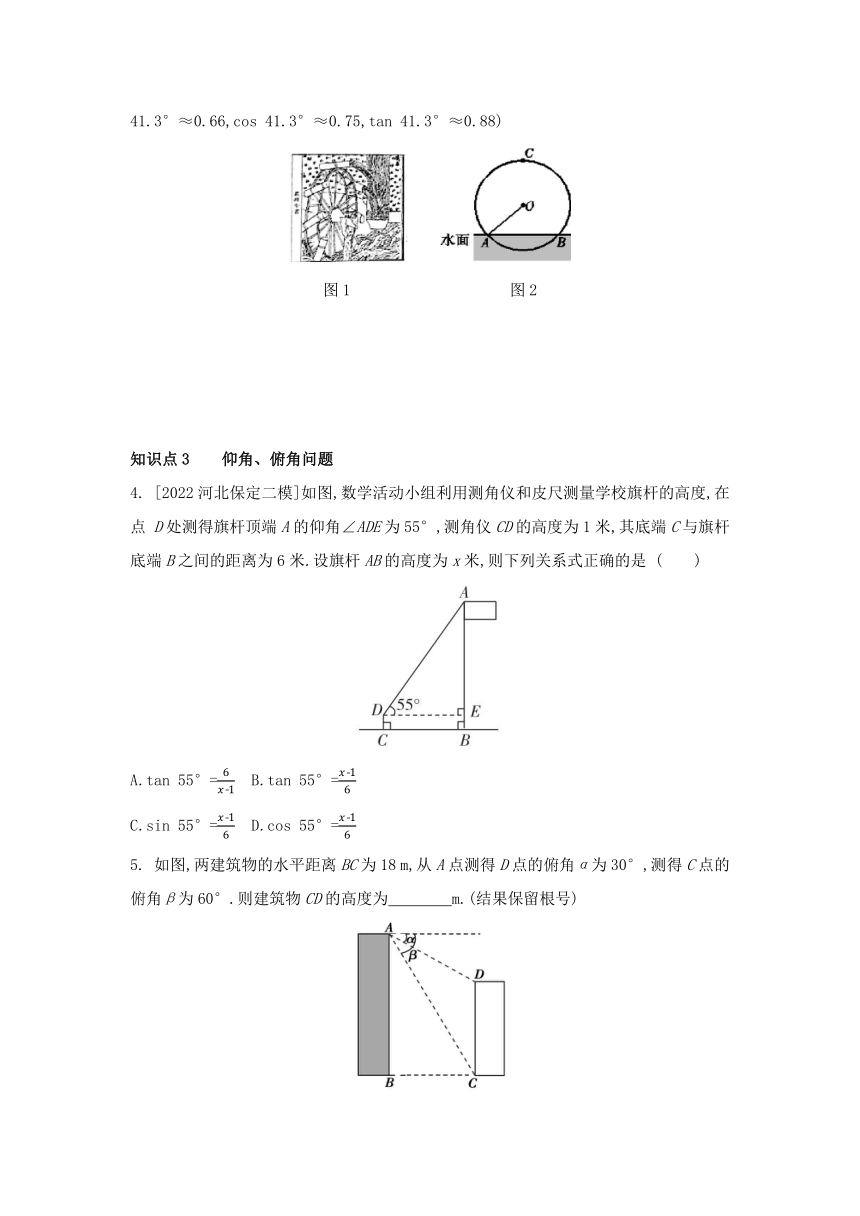
1. [2022山东菏泽期末]西周时期,丞相周公旦设计过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中立柱AC高为a.已知冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A.asin 26.5° B.
C.acos 26.5° D.
2. 如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.4cos α米 B.4sin α米
C.4tan α米 D.米
知识点2 与圆有关的问题
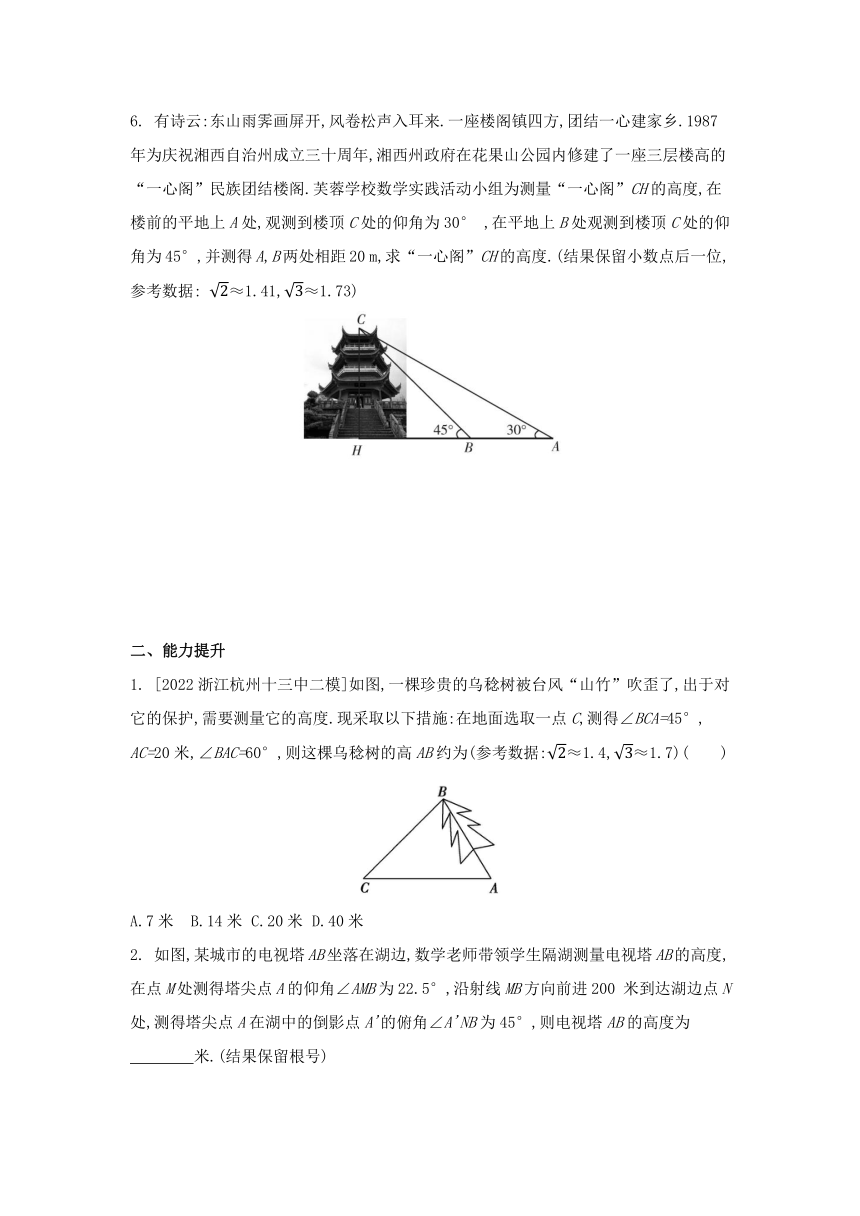
3. 筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB的长为6米,∠OAB=41.3°,若点C为运行轨迹的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin 41.3°≈0.66,cos 41.3°≈0.75,tan 41.3°≈0.88)
图1 图2
知识点3 仰角、俯角问题
4. [2022河北保定二模]如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点 D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米.设旗杆AB的高度为x米,则下列关系式正确的是 ( )
A.tan 55°= B.tan 55°=
C.sin 55°= D.cos 55°=
5. 如图,两建筑物的水平距离BC为18 m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为 m.(结果保留根号)
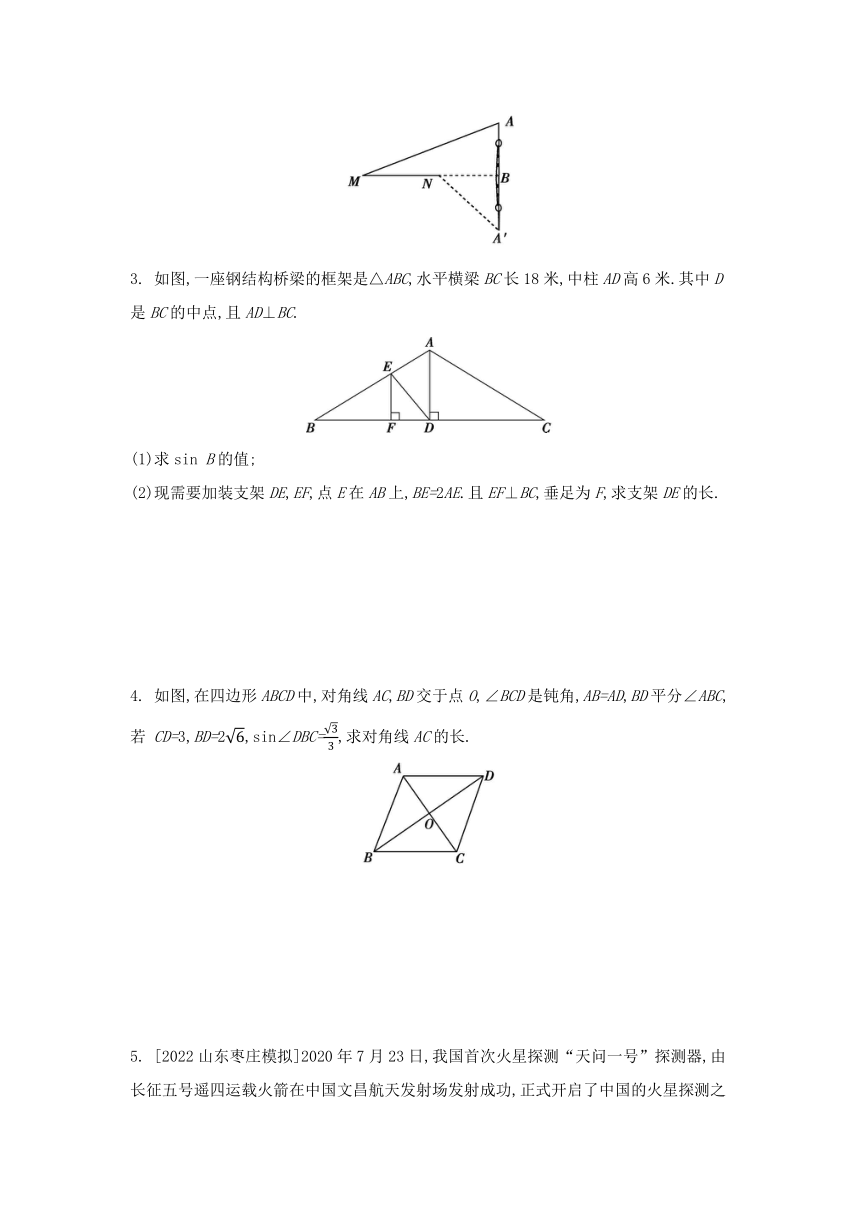
6. 有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁”CH的高度,在楼前的平地上A处,观测到楼顶C处的仰角为30° ,在平地上B处观测到楼顶C处的仰角为45°,并测得A,B两处相距20 m,求“一心阁”CH的高度.(结果保留小数点后一位,参考数据: ≈1.41,≈1.73)
二、能力提升
1. [2022浙江杭州十三中二模]如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,出于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,
AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为(参考数据:≈1.4,≈1.7)( )
A.7米 B.14米 C.20米 D.40米
2. 如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200 米到达湖边点N处,测得塔尖点A在湖中的倒影点A'的俯角∠A'NB为45°,则电视塔AB的高度为
米.(结果保留根号)
3. 如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米.其中D是BC的中点,且AD⊥BC.
(1)求sin B的值;
(2)现需要加装支架DE,EF,点E在AB上,BE=2AE.且EF⊥BC,垂足为F,求支架DE的长.
4. 如图,在四边形ABCD中,对角线AC,BD交于点O,∠BCD是钝角,AB=AD,BD平分∠ABC,若 CD=3,BD=2,sin∠DBC=,求对角线AC的长.
5. [2022山东枣庄模拟]2020年7月23日,我国首次火星探测“天问一号”探测器,由长征五号遥四运载火箭在中国文昌航天发射场发射成功,正式开启了中国的火星探测之旅.运载火箭从地面O处发射,当火箭到达点A时,地面D处的雷达站测得AD=4 000 m,仰角为30°,3秒后,火箭直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°,O,C,D在同一直线上,已知C,D两处相距460 m,求火箭从A到B的平均速度.(结果精确到1 m,参考数据:≈1.732,≈1.414)
6. [2022云南昆明模拟]【材料阅读】 2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度.其基本原理之一是三角高程测量法,在山顶上立一个觇标,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于300 m时,还要考虑球气差,球气差计算公式为f=(其中d为两点间的水平距离,R为地球的半径,R取6 400 000 m),即山的海拔=测量点测得山的高度+测量点的海拔+球气差.
【问题解决】 某校科技小组的同学参加了一项野外测量某座山的海拔活动.如图,点A,B的水平距离d=800 m,测量仪AC=1.5 m,觇标DE=2 m,点E,D,B在垂直于地面的一条直线上,在测量点A处用测量仪测得山顶觇标顶端E的仰角为37°,测量点A处的海拔为1 800 m.
(1)数据6 400 000用科学记数法表示为 ;
(2)请你计算该山的海拔.(要计算球气差,结果精确到0.01 m)
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
参考答案
一、基础巩固
1.B 【解析】 在Rt△ACB中,tan∠ABC=,所以BC==.
2.A 【解析】 过点A作BC的垂线,垂足为点D.在Rt△ACD中,CD=AC×cos α=2cos α 米.∵AB=AC,AD⊥BC,∴BC=2CD=4cos α 米.
3.【解析】 如图,连接CO并延长,与AB交于点D,
则CD⊥AB且AD=BD,∴AD=BD=AB=3米.
在Rt△AOD中,cos∠OAD=,tan∠OAD=,
∴OA==≈4(米),
OD=ADtan∠OAD=3tan 41.3°≈2.64(米),
∴CD=CO+OD=OA+OD≈6.64米.
故点C到弦AB所在直线的距离约为6.64米.
4.B 【解析】 在Rt△ADE中,DE=BC=6,AE=AB-BE=AB-CD=x-1,∠ADE=55°,则sin 55°=,cos 55°=,tan 55°==.
5.12 【解析】 过点D作DE⊥AB于点E,则四边形BCDE是矩形.根据题意,得∠ACB=∠β=60°,∠ADE=∠α=30°,DE=BC=18 m,CD=BE.在Rt△ABC中,AB=BC·tan∠ACB=18×tan 60°=18(m),在Rt△ADE中,AE=DE·tan∠ADE=18×tan 30°=6(m),∴DC=BE=AB-AE=18-6=12(m).
6.【解析】 设CH=x m,
由题意,得∠AHC=90°,∠CBH=45°,∠A=30°,
∴BH=CH=x m,AH=CH=x m.
∵AH-BH=AB,∴x-x=20,
解得x=10(+1)≈27.3.
答:“一心阁”CH的高度约为27.3 m.
二、能力提升
1.B 【解析】 如图,过点B作BH⊥AC于点H.∵∠BCH=45°,∠BHC=90°,∴∠HBC
=∠BCH=45°,∴HC=HB.设HC=HB=x 米,∵∠A=60°,∴AH=x 米.∵AC=20米,∴x+x=20,∴x=10(3-),∴AH=×10(3-)=10(-1)(米),∴AB=2AH=20(-1)≈14(米).
2.100 【解析】 连接AN,易证△ABN≌△A'BN,∴A'N=AN,∠ANB=∠A'NB=45°.
∵∠AMB=22.5°,∴∠MAN=22.5°,∴AN=MN=200 米,∴AB=AN·sin∠ANB=200×sin 45°=200×=100(米).
3.【解析】 (1)∵点D是BC的中点,∴BD=BC=9米.
∵AD⊥BC,∴△ABD是直角三角形,
∴AB===3(米),
∴sin B===.
(2)∵EF⊥BC,AD⊥BC,∴EF∥AD,
∴△BEF∽△BAD,
∴===,
∴EF=AD=4米,BF=BD=6米,
则DF=BD-BF=9-6=3(米).
在Rt△DEF中,DE===5(米).
4.【解析】 如图,过点D作DE⊥BC交BC的延长线于点E,
则∠E=90°,
∵sin∠DBC==,BD=2,
∴DE=2.
在Rt△CDE中,∵CD=3,DE=2,
∴CE==1.
在Rt△BDE中,∵BD=2,DE=2,∴BE==4,
∴BC=3,∴BC=CD,∴∠CBD=∠CDB.
∵BD平分∠ABC,∴∠ABD=∠DBC,
∴∠ABD=∠CDB,∴AB∥CD.
同理AD∥BC,∴四边形ABCD是菱形.
∴AC⊥BD,AO=CO,BO=DO=,
∴OC===,∴AC=2.
5.【解析】 由题意,得AD=4 000 m,CD=460 m,∠ADO=30°,∠BCO=45°,
在Rt△AOD中,∵AD=4 000 m,∠ADO=30°,
∴OA=AD=2 000 m,OD=AD=2 000 m.
在Rt△BOC中,∠BCO=45°,
∴OB=OC=OD-CD=(2 000-460)m,
∴AB=OB-OA=2 000-460-2 000≈1 004(m),
1 004÷3≈335(m/s).
答:火箭从A到B的平均速度约为335 m/s.
6.【解析】 (1)6.4×106
(2)如图,过点C作CH⊥BE于点H.
由题意得,AB=CH=800 m,AC=BH=1.5 m.
在Rt△ECH中,EH=CH·tan 37°≈600 m,
∴DB=EH-DE+BH=599.5 m,
又f===0.043(m),
∴该山的海拔为599.5+0.043+1 800≈2 399.54(m).
(课时2 应用举例(1))
一、基础巩固
知识点1 一般的实际问题
1. [2022山东菏泽期末]西周时期,丞相周公旦设计过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中立柱AC高为a.已知冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A.asin 26.5° B.
C.acos 26.5° D.
2. 如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.4cos α米 B.4sin α米
C.4tan α米 D.米
知识点2 与圆有关的问题
3. 筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB的长为6米,∠OAB=41.3°,若点C为运行轨迹的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin 41.3°≈0.66,cos 41.3°≈0.75,tan 41.3°≈0.88)
图1 图2
知识点3 仰角、俯角问题
4. [2022河北保定二模]如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点 D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米.设旗杆AB的高度为x米,则下列关系式正确的是 ( )
A.tan 55°= B.tan 55°=
C.sin 55°= D.cos 55°=
5. 如图,两建筑物的水平距离BC为18 m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°.则建筑物CD的高度为 m.(结果保留根号)
6. 有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁”CH的高度,在楼前的平地上A处,观测到楼顶C处的仰角为30° ,在平地上B处观测到楼顶C处的仰角为45°,并测得A,B两处相距20 m,求“一心阁”CH的高度.(结果保留小数点后一位,参考数据: ≈1.41,≈1.73)
二、能力提升
1. [2022浙江杭州十三中二模]如图,一棵珍贵的乌稔树被台风“山竹”吹歪了,出于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,
AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为(参考数据:≈1.4,≈1.7)( )
A.7米 B.14米 C.20米 D.40米
2. 如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200 米到达湖边点N处,测得塔尖点A在湖中的倒影点A'的俯角∠A'NB为45°,则电视塔AB的高度为
米.(结果保留根号)
3. 如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米.其中D是BC的中点,且AD⊥BC.
(1)求sin B的值;
(2)现需要加装支架DE,EF,点E在AB上,BE=2AE.且EF⊥BC,垂足为F,求支架DE的长.
4. 如图,在四边形ABCD中,对角线AC,BD交于点O,∠BCD是钝角,AB=AD,BD平分∠ABC,若 CD=3,BD=2,sin∠DBC=,求对角线AC的长.
5. [2022山东枣庄模拟]2020年7月23日,我国首次火星探测“天问一号”探测器,由长征五号遥四运载火箭在中国文昌航天发射场发射成功,正式开启了中国的火星探测之旅.运载火箭从地面O处发射,当火箭到达点A时,地面D处的雷达站测得AD=4 000 m,仰角为30°,3秒后,火箭直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°,O,C,D在同一直线上,已知C,D两处相距460 m,求火箭从A到B的平均速度.(结果精确到1 m,参考数据:≈1.732,≈1.414)
6. [2022云南昆明模拟]【材料阅读】 2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度.其基本原理之一是三角高程测量法,在山顶上立一个觇标,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于300 m时,还要考虑球气差,球气差计算公式为f=(其中d为两点间的水平距离,R为地球的半径,R取6 400 000 m),即山的海拔=测量点测得山的高度+测量点的海拔+球气差.
【问题解决】 某校科技小组的同学参加了一项野外测量某座山的海拔活动.如图,点A,B的水平距离d=800 m,测量仪AC=1.5 m,觇标DE=2 m,点E,D,B在垂直于地面的一条直线上,在测量点A处用测量仪测得山顶觇标顶端E的仰角为37°,测量点A处的海拔为1 800 m.
(1)数据6 400 000用科学记数法表示为 ;
(2)请你计算该山的海拔.(要计算球气差,结果精确到0.01 m)
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
参考答案
一、基础巩固
1.B 【解析】 在Rt△ACB中,tan∠ABC=,所以BC==.
2.A 【解析】 过点A作BC的垂线,垂足为点D.在Rt△ACD中,CD=AC×cos α=2cos α 米.∵AB=AC,AD⊥BC,∴BC=2CD=4cos α 米.
3.【解析】 如图,连接CO并延长,与AB交于点D,
则CD⊥AB且AD=BD,∴AD=BD=AB=3米.
在Rt△AOD中,cos∠OAD=,tan∠OAD=,
∴OA==≈4(米),
OD=ADtan∠OAD=3tan 41.3°≈2.64(米),
∴CD=CO+OD=OA+OD≈6.64米.
故点C到弦AB所在直线的距离约为6.64米.
4.B 【解析】 在Rt△ADE中,DE=BC=6,AE=AB-BE=AB-CD=x-1,∠ADE=55°,则sin 55°=,cos 55°=,tan 55°==.
5.12 【解析】 过点D作DE⊥AB于点E,则四边形BCDE是矩形.根据题意,得∠ACB=∠β=60°,∠ADE=∠α=30°,DE=BC=18 m,CD=BE.在Rt△ABC中,AB=BC·tan∠ACB=18×tan 60°=18(m),在Rt△ADE中,AE=DE·tan∠ADE=18×tan 30°=6(m),∴DC=BE=AB-AE=18-6=12(m).
6.【解析】 设CH=x m,
由题意,得∠AHC=90°,∠CBH=45°,∠A=30°,
∴BH=CH=x m,AH=CH=x m.
∵AH-BH=AB,∴x-x=20,
解得x=10(+1)≈27.3.
答:“一心阁”CH的高度约为27.3 m.
二、能力提升
1.B 【解析】 如图,过点B作BH⊥AC于点H.∵∠BCH=45°,∠BHC=90°,∴∠HBC
=∠BCH=45°,∴HC=HB.设HC=HB=x 米,∵∠A=60°,∴AH=x 米.∵AC=20米,∴x+x=20,∴x=10(3-),∴AH=×10(3-)=10(-1)(米),∴AB=2AH=20(-1)≈14(米).
2.100 【解析】 连接AN,易证△ABN≌△A'BN,∴A'N=AN,∠ANB=∠A'NB=45°.
∵∠AMB=22.5°,∴∠MAN=22.5°,∴AN=MN=200 米,∴AB=AN·sin∠ANB=200×sin 45°=200×=100(米).
3.【解析】 (1)∵点D是BC的中点,∴BD=BC=9米.
∵AD⊥BC,∴△ABD是直角三角形,
∴AB===3(米),
∴sin B===.
(2)∵EF⊥BC,AD⊥BC,∴EF∥AD,
∴△BEF∽△BAD,
∴===,
∴EF=AD=4米,BF=BD=6米,
则DF=BD-BF=9-6=3(米).
在Rt△DEF中,DE===5(米).
4.【解析】 如图,过点D作DE⊥BC交BC的延长线于点E,
则∠E=90°,
∵sin∠DBC==,BD=2,
∴DE=2.
在Rt△CDE中,∵CD=3,DE=2,
∴CE==1.
在Rt△BDE中,∵BD=2,DE=2,∴BE==4,
∴BC=3,∴BC=CD,∴∠CBD=∠CDB.
∵BD平分∠ABC,∴∠ABD=∠DBC,
∴∠ABD=∠CDB,∴AB∥CD.
同理AD∥BC,∴四边形ABCD是菱形.
∴AC⊥BD,AO=CO,BO=DO=,
∴OC===,∴AC=2.
5.【解析】 由题意,得AD=4 000 m,CD=460 m,∠ADO=30°,∠BCO=45°,
在Rt△AOD中,∵AD=4 000 m,∠ADO=30°,
∴OA=AD=2 000 m,OD=AD=2 000 m.
在Rt△BOC中,∠BCO=45°,
∴OB=OC=OD-CD=(2 000-460)m,
∴AB=OB-OA=2 000-460-2 000≈1 004(m),
1 004÷3≈335(m/s).
答:火箭从A到B的平均速度约为335 m/s.
6.【解析】 (1)6.4×106
(2)如图,过点C作CH⊥BE于点H.
由题意得,AB=CH=800 m,AC=BH=1.5 m.
在Rt△ECH中,EH=CH·tan 37°≈600 m,
∴DB=EH-DE+BH=599.5 m,
又f===0.043(m),
∴该山的海拔为599.5+0.043+1 800≈2 399.54(m).
