28.2 解直角三角形及其应用(课时1)同步练习 人教版数学九年级下册(含解析)
文档属性
| 名称 | 28.2 解直角三角形及其应用(课时1)同步练习 人教版数学九年级下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 17:15:55 | ||
图片预览

文档简介
《28.2 解直角三角形及其应用》同步练习
(课时1 解直角三角形)
一、基础巩固
知识点1 已知两边解直角三角形
1. 在Rt△ABC中,AB=4,AC=2,∠C=90°,则∠A的度数为( )
A.30° B.40° C.45° D.60°
2. 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=4,a=4,求这个三角形的其他元素.
知识点2 已知一边及一锐角解直角三角形
3. [2022黑龙江哈尔滨南岗区模拟]在△ABC中,∠A=40°,∠C=90°,BC=7,则AB边的长是( )
A.7sin 40° B.7cos 40°
C. D.
4. [2022安徽合肥庐阳中学月考]已知Rt△ABC中,∠C=90°,∠A=30°,斜边上的高CE为1,则△ABC的三边长分别为( )
A.BC=,AC=2,AB=
B.BC=,AC=2,AB=
C.BC=2,AC=,AB=
D.BC=2,AC=2,AB=4
5. 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.求下列直角三角形中的未知量.
(1)∠B=60°,c=25;
(2)∠A=30°,b=.
知识点3 解直角三角形的综合运用
6. [2022广东广州越秀区月考]在Rt△ABC中,∠C=90°,斜边上的中线长是3 cm,sin A=,则S△ABC=( )
A. cm2 B.2 cm2
C.3 cm2 D.4 cm2
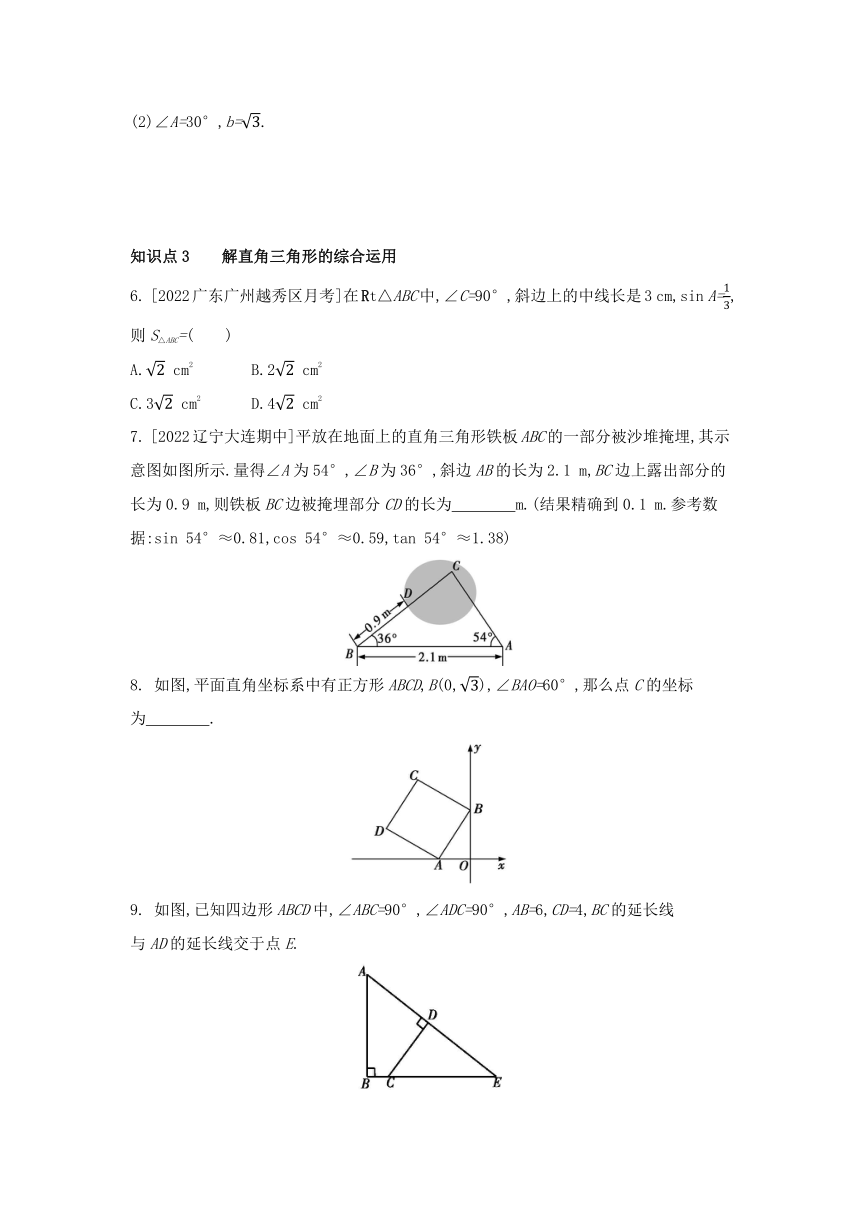
7. [2022辽宁大连期中]平放在地面上的直角三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示.量得∠A为54°,∠B为36°,斜边AB的长为2.1 m,BC边上露出部分的长为0.9 m,则铁板BC边被掩埋部分CD的长为 m.(结果精确到0.1 m.参考数据:sin 54°≈0.81,cos 54°≈0.59,tan 54°≈1.38)
8. 如图,平面直角坐标系中有正方形ABCD,B(0,),∠BAO=60°,那么点C的坐标为 .
9. 如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线
与AD的延长线交于点E.
(1)若∠A=60°,求BC的长;
(2)若sin A=,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
二、能力提升
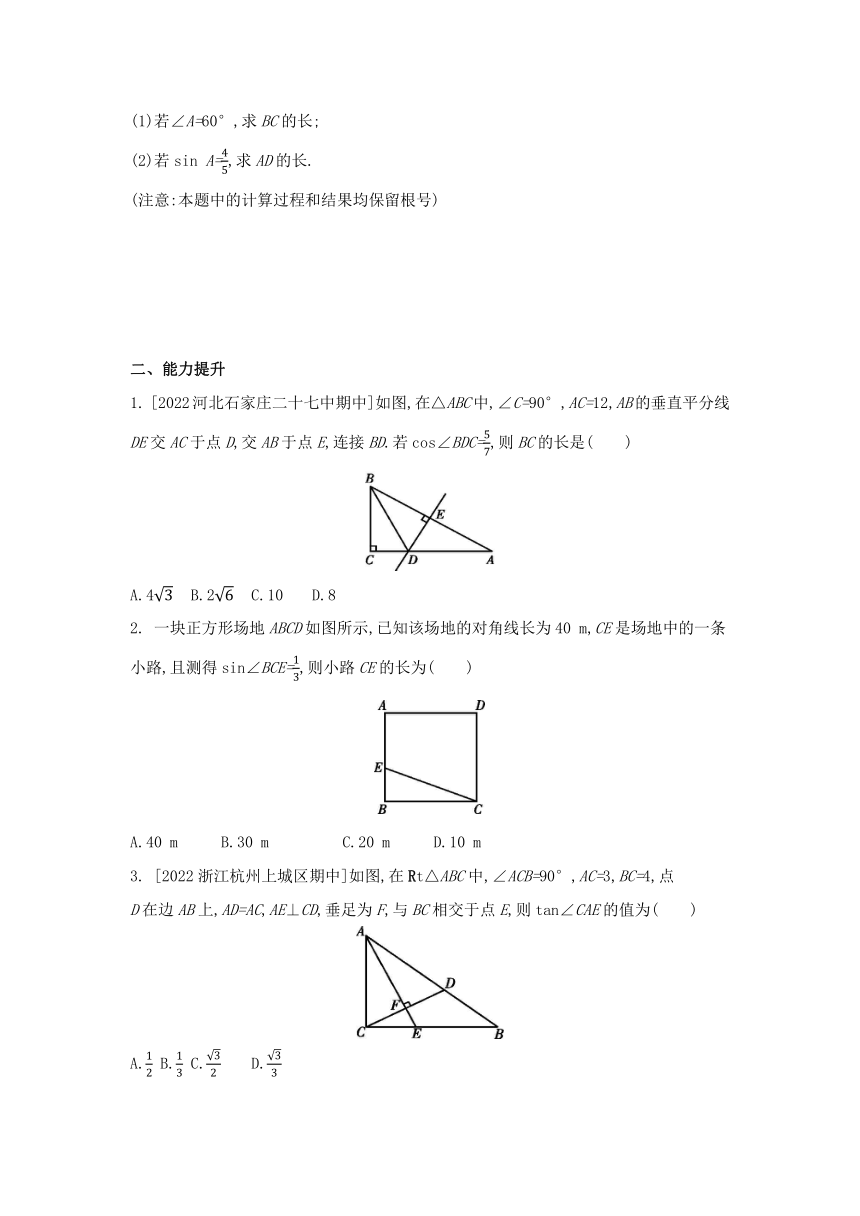
1. [2022河北石家庄二十七中期中]如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线DE交AC于点D,交AB于点E,连接BD.若cos∠BDC=,则BC的长是( )
A.4 B.2 C.10 D.8
2. 一块正方形场地ABCD如图所示,已知该场地的对角线长为40 m,CE是场地中的一条小路,且测得sin∠BCE=,则小路CE的长为( )
A.40 m B.30 m C.20 m D.10 m
3. [2022浙江杭州上城区期中]如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点
D在边AB上,AD=AC,AE⊥CD,垂足为F,与BC相交于点E,则tan∠CAE的值为( )
A. B. C. D.
4. [2022黑龙江哈尔滨南岗区一模]在△ABC中,AC=2,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为,且CD⊥AC,则BC的长为 .
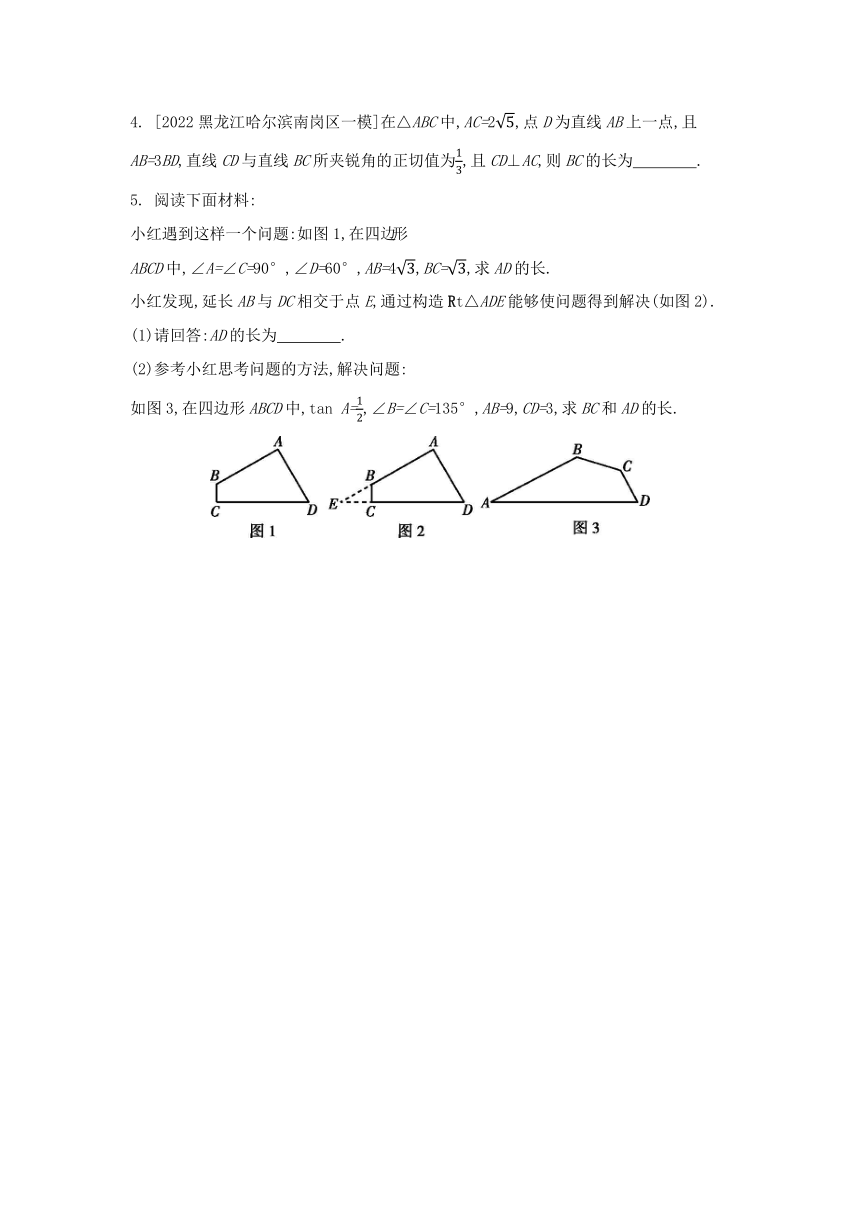
5. 阅读下面材料:
小红遇到这样一个问题:如图1,在四边形ABCD中,∠A=∠C=90°,∠D=60°,AB=4,BC=,求AD的长.
小红发现,延长AB与DC相交于点E,通过构造Rt△ADE能够使问题得到解决(如图2).
(1)请回答:AD的长为 .
(2)参考小红思考问题的方法,解决问题:
如图3,在四边形ABCD中,tan A=,∠B=∠C=135°,AB=9,CD=3,求BC和AD的长.
参考答案
一、基础巩固
1.C 【解析】 在Rt△ABC中,∵AB=4,AC=2,∠C=90°,∴cos A===,∴∠A=45°.
2.【解析】 在Rt△ABC中,∵∠C=90°,b=4,a=4,
∴tan A===,
∴∠A=60°,∴∠B=90°-∠A=30°,
∴c=2b=8.
故c=8,∠A=60°,∠B=30°.
3.C 【解析】 在△ABC中,∵∠A=40°,∠C=90°,BC=7,∴sin A=,∴AB==.
4.A 【解析】 如图,由题意知,sin A==,∵CE=1,∴AC=2,∵tan A=,∴BC=2tan 30°=,∴AB==.
5.【解析】 (1)在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°,∴sin A==,
∵c=25,∴a=.
∵cos A==,c=25,
∴b=.
综上,a=,b=,∠A=30°.
(2)∵∠C=90°,∠A=30°,∴∠B=60°.
在Rt△ABC中,cos A==,
∵b=,∴c=2,∴a=c=1.
综上,a=1,c=2,∠B=60°.
6.D 【解析】 ∵Rt△ABC中斜边上的中线长是3 cm,∴AB=6 cm.∵sin A=,∴BC=2 cm,∴AC==4 cm,∴=BC×AC=4 cm2.
7.0.8 【解析】 ∵∠A=54°,∠B=36°,∴∠C=180°-∠A-∠B=90°.在Rt△ABC中,sin A=,∴BC=AB·sin A=2.1×sin 54°≈2.1×0.81=1.701(m),则CD=BC-BD≈1.701-0.9=0.801≈0.8(m).
8.(-,+1) 【解析】 过点C作CE⊥y轴于点E,则易证Rt△CEB≌Rt△BOA,所以CE=BO=,BE=AO==1,所以OE=OB+BE=+1,因此点C的坐标为(-,+1).
9.【解析】 (1)∵∠A=60°,∠ABE=90°,∴∠E=30°.
在Rt△ABE中,∵AB=6,tan A=,
∴BE=AB·tan A=6×tan 60°=6.
∵∠CDE=90°,CD=4,sin E=,
∴CE===8,∴BC=BE-CE=6-8.
(2)∵∠ABE=90°,AB=6,sin A==,
∴设BE=4x,则AE=5x,AB=3x,
∴3x=6,解得x=2,∴BE=8,AE=10,
∴tan E====,∴DE=,
∴AD=AE-DE=10-=.
二、能力提升
1.B 【解析】 在Rt△BCD中,∵∠C=90°,cos∠BDC==,∴设CD=5x,则BD=7x,∴BC=2x.∵DE是AB的垂直平分线,∴AD=BD=7x,∴AC=AD+CD=12x=12,∴x=1,∴BC=2.
2.B 【解析】 连接AC.由题意可知AC=40 m,∴BC=20 m.在Rt△BEC中,sin∠BCE==,不妨设CE=3k m(k>0),则BE=k m.根据勾股定理,得CE2=BE2+CB2,即(3k)2=k2+(20)2,∴k=10,∴CE=30 m.
3.A 【解析】 由AD=AC,AE⊥CD,得AE垂直平分CD,联想到连接DE,如图,由此可得AD=AC=3,CE=DE.在Rt△ABC中,由AC=3,BC=4,得AB=5,因此,BD=2.易证△ADE≌△ACE,由此可得∠ADE=∠ACE=90°,即∠BDE=90°.在Rt△BDE中,DE2+BD2=BE2,即CE2+BD2=(BC-CE)2,得CE=,因此,tan∠CAE==.
4.或5 【解析】 如图1,过点B作BM⊥CD,垂足为M,∵CD⊥AC,∴BM∥AC,∴△DBM∽△DAC,∴=.∵AB=3BD,AC=2,∴=,∴BM=.在Rt△BMC中,由tan∠BCM=,可得BC=BM=.如图2,过点B作BN⊥AC,交AC的延长线于点N,∵CD⊥AC,∴BN∥CD,∴=.∵AB=3BD,AC=2,∴=,∴CN=.由BN∥CD,得∠CBN=∠BCD.∵tan∠BCD=,∴tan∠CBN=,∴BC=CN=5.综上,BC的长为或5.
5.【解析】 (1)6
延长AB与DC相交于点E,
在△ADE中,∵∠A=90°,∠D=60°,∴∠E=30°.
在Rt△BEC中,∵∠BCE=90°,∠E=30°,BC=,
∴BE=2BC=2,∴AE=AB+BE=4+2=6.
在Rt△ADE中,∵∠A=90°,∠E=30°,AE=6,
∴AD=AEtan∠E=6=6.
(2)如图,延长AB与DC相交于点E.
∵∠ABC=∠BCD=135°,∴∠EBC=∠ECB=45°,
∴BE=CE,∠E=90°.
设BE=CE=x,则BC=x,AE=9+x,DE=3+x.
在Rt△ADE中,∵∠E=90°,tan A=,
∴=,即=,∴x=3,
∴BC=3,AE=12,DE=6,
∴AD===6.
(课时1 解直角三角形)
一、基础巩固
知识点1 已知两边解直角三角形
1. 在Rt△ABC中,AB=4,AC=2,∠C=90°,则∠A的度数为( )
A.30° B.40° C.45° D.60°
2. 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=4,a=4,求这个三角形的其他元素.
知识点2 已知一边及一锐角解直角三角形
3. [2022黑龙江哈尔滨南岗区模拟]在△ABC中,∠A=40°,∠C=90°,BC=7,则AB边的长是( )
A.7sin 40° B.7cos 40°
C. D.
4. [2022安徽合肥庐阳中学月考]已知Rt△ABC中,∠C=90°,∠A=30°,斜边上的高CE为1,则△ABC的三边长分别为( )
A.BC=,AC=2,AB=
B.BC=,AC=2,AB=
C.BC=2,AC=,AB=
D.BC=2,AC=2,AB=4
5. 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.求下列直角三角形中的未知量.
(1)∠B=60°,c=25;
(2)∠A=30°,b=.
知识点3 解直角三角形的综合运用
6. [2022广东广州越秀区月考]在Rt△ABC中,∠C=90°,斜边上的中线长是3 cm,sin A=,则S△ABC=( )
A. cm2 B.2 cm2
C.3 cm2 D.4 cm2
7. [2022辽宁大连期中]平放在地面上的直角三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示.量得∠A为54°,∠B为36°,斜边AB的长为2.1 m,BC边上露出部分的长为0.9 m,则铁板BC边被掩埋部分CD的长为 m.(结果精确到0.1 m.参考数据:sin 54°≈0.81,cos 54°≈0.59,tan 54°≈1.38)
8. 如图,平面直角坐标系中有正方形ABCD,B(0,),∠BAO=60°,那么点C的坐标为 .
9. 如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线
与AD的延长线交于点E.
(1)若∠A=60°,求BC的长;
(2)若sin A=,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
二、能力提升
1. [2022河北石家庄二十七中期中]如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线DE交AC于点D,交AB于点E,连接BD.若cos∠BDC=,则BC的长是( )
A.4 B.2 C.10 D.8
2. 一块正方形场地ABCD如图所示,已知该场地的对角线长为40 m,CE是场地中的一条小路,且测得sin∠BCE=,则小路CE的长为( )
A.40 m B.30 m C.20 m D.10 m
3. [2022浙江杭州上城区期中]如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点
D在边AB上,AD=AC,AE⊥CD,垂足为F,与BC相交于点E,则tan∠CAE的值为( )
A. B. C. D.
4. [2022黑龙江哈尔滨南岗区一模]在△ABC中,AC=2,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为,且CD⊥AC,则BC的长为 .
5. 阅读下面材料:
小红遇到这样一个问题:如图1,在四边形ABCD中,∠A=∠C=90°,∠D=60°,AB=4,BC=,求AD的长.
小红发现,延长AB与DC相交于点E,通过构造Rt△ADE能够使问题得到解决(如图2).
(1)请回答:AD的长为 .
(2)参考小红思考问题的方法,解决问题:
如图3,在四边形ABCD中,tan A=,∠B=∠C=135°,AB=9,CD=3,求BC和AD的长.
参考答案
一、基础巩固
1.C 【解析】 在Rt△ABC中,∵AB=4,AC=2,∠C=90°,∴cos A===,∴∠A=45°.
2.【解析】 在Rt△ABC中,∵∠C=90°,b=4,a=4,
∴tan A===,
∴∠A=60°,∴∠B=90°-∠A=30°,
∴c=2b=8.
故c=8,∠A=60°,∠B=30°.
3.C 【解析】 在△ABC中,∵∠A=40°,∠C=90°,BC=7,∴sin A=,∴AB==.
4.A 【解析】 如图,由题意知,sin A==,∵CE=1,∴AC=2,∵tan A=,∴BC=2tan 30°=,∴AB==.
5.【解析】 (1)在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°,∴sin A==,
∵c=25,∴a=.
∵cos A==,c=25,
∴b=.
综上,a=,b=,∠A=30°.
(2)∵∠C=90°,∠A=30°,∴∠B=60°.
在Rt△ABC中,cos A==,
∵b=,∴c=2,∴a=c=1.
综上,a=1,c=2,∠B=60°.
6.D 【解析】 ∵Rt△ABC中斜边上的中线长是3 cm,∴AB=6 cm.∵sin A=,∴BC=2 cm,∴AC==4 cm,∴=BC×AC=4 cm2.
7.0.8 【解析】 ∵∠A=54°,∠B=36°,∴∠C=180°-∠A-∠B=90°.在Rt△ABC中,sin A=,∴BC=AB·sin A=2.1×sin 54°≈2.1×0.81=1.701(m),则CD=BC-BD≈1.701-0.9=0.801≈0.8(m).
8.(-,+1) 【解析】 过点C作CE⊥y轴于点E,则易证Rt△CEB≌Rt△BOA,所以CE=BO=,BE=AO==1,所以OE=OB+BE=+1,因此点C的坐标为(-,+1).
9.【解析】 (1)∵∠A=60°,∠ABE=90°,∴∠E=30°.
在Rt△ABE中,∵AB=6,tan A=,
∴BE=AB·tan A=6×tan 60°=6.
∵∠CDE=90°,CD=4,sin E=,
∴CE===8,∴BC=BE-CE=6-8.
(2)∵∠ABE=90°,AB=6,sin A==,
∴设BE=4x,则AE=5x,AB=3x,
∴3x=6,解得x=2,∴BE=8,AE=10,
∴tan E====,∴DE=,
∴AD=AE-DE=10-=.
二、能力提升
1.B 【解析】 在Rt△BCD中,∵∠C=90°,cos∠BDC==,∴设CD=5x,则BD=7x,∴BC=2x.∵DE是AB的垂直平分线,∴AD=BD=7x,∴AC=AD+CD=12x=12,∴x=1,∴BC=2.
2.B 【解析】 连接AC.由题意可知AC=40 m,∴BC=20 m.在Rt△BEC中,sin∠BCE==,不妨设CE=3k m(k>0),则BE=k m.根据勾股定理,得CE2=BE2+CB2,即(3k)2=k2+(20)2,∴k=10,∴CE=30 m.
3.A 【解析】 由AD=AC,AE⊥CD,得AE垂直平分CD,联想到连接DE,如图,由此可得AD=AC=3,CE=DE.在Rt△ABC中,由AC=3,BC=4,得AB=5,因此,BD=2.易证△ADE≌△ACE,由此可得∠ADE=∠ACE=90°,即∠BDE=90°.在Rt△BDE中,DE2+BD2=BE2,即CE2+BD2=(BC-CE)2,得CE=,因此,tan∠CAE==.
4.或5 【解析】 如图1,过点B作BM⊥CD,垂足为M,∵CD⊥AC,∴BM∥AC,∴△DBM∽△DAC,∴=.∵AB=3BD,AC=2,∴=,∴BM=.在Rt△BMC中,由tan∠BCM=,可得BC=BM=.如图2,过点B作BN⊥AC,交AC的延长线于点N,∵CD⊥AC,∴BN∥CD,∴=.∵AB=3BD,AC=2,∴=,∴CN=.由BN∥CD,得∠CBN=∠BCD.∵tan∠BCD=,∴tan∠CBN=,∴BC=CN=5.综上,BC的长为或5.
5.【解析】 (1)6
延长AB与DC相交于点E,
在△ADE中,∵∠A=90°,∠D=60°,∴∠E=30°.
在Rt△BEC中,∵∠BCE=90°,∠E=30°,BC=,
∴BE=2BC=2,∴AE=AB+BE=4+2=6.
在Rt△ADE中,∵∠A=90°,∠E=30°,AE=6,
∴AD=AEtan∠E=6=6.
(2)如图,延长AB与DC相交于点E.
∵∠ABC=∠BCD=135°,∴∠EBC=∠ECB=45°,
∴BE=CE,∠E=90°.
设BE=CE=x,则BC=x,AE=9+x,DE=3+x.
在Rt△ADE中,∵∠E=90°,tan A=,
∴=,即=,∴x=3,
∴BC=3,AE=12,DE=6,
∴AD===6.
