28.2 解直角三角形及其应用(课时3)同步练习 人教版数学九年级下册(含解析)
文档属性
| 名称 | 28.2 解直角三角形及其应用(课时3)同步练习 人教版数学九年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 213.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 17:16:40 | ||
图片预览



文档简介
《28.2 解直角三角形及其应用》同步练习
(课时3 应用举例(2))
一、基础巩固
知识点1 方向角问题
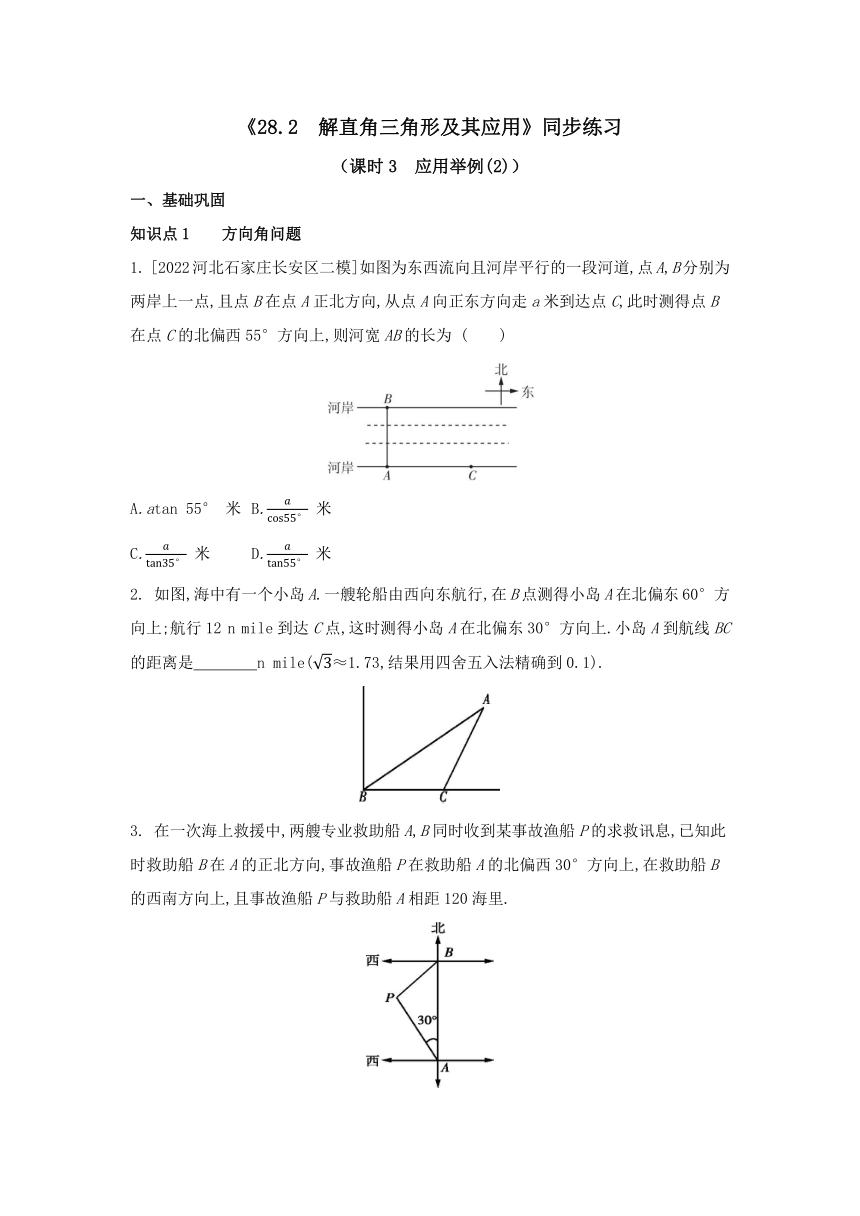
1. [2022河北石家庄长安区二模]如图为东西流向且河岸平行的一段河道,点A,B分别为两岸上一点,且点B在点A正北方向,从点A向正东方向走a米到达点C,此时测得点B在点C的北偏西55°方向上,则河宽AB的长为 ( )
A.atan 55° 米 B. 米
C. 米 D. 米
2. 如图,海中有一个小岛A.一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12 n mile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是 n mile(≈1.73,结果用四舍五入法精确到0.1).
3. 在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船P的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里.
(1)求收到求救讯息时事故渔船P与救助船B之间的距离(结果保留根号);
(2)若救助船A,B分别以40海里/时、30海里/时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.
知识点2 坡度、坡角问题
4. [2022广东广州二模]如图是一水库大坝横断面的一部分,坝高h=60 m,迎水坡AB=100 m,斜坡的坡角为α,则tan α的值为( )
A. B. C. D.
5. 太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通,如图是该地铁某站扶梯的示意图,扶梯AB的坡度i=5∶12(i为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端A以0.5米/秒的速度用时40秒到达扶梯顶端B,则王老师上升的铅直高度BC为 米.
6. 如图是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面AC的倾斜角∠CAB=45°,在距A点10米处有一建筑物HQ.为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问:该建筑物是否需要拆除 (计算最后结果保留一位小数,参考数据:≈1.414,≈1.732)
二、能力提升
1. 如图,在距某居民楼AB楼底B点左侧水平距离60 m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1∶0.75,山坡坡底C点到坡顶D点的距离CD=45 m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为(参考数据:sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53)( )
A.76.9 m B.82.1 m C.94.8 m D.112.6 m
2. [2022安徽阜阳期末]如图,一艘船由A港沿北偏东65°方向航行30 km至B港,然后沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )
A.(30+30) km B.(30+10) km
C.(10+30) km D.30 km
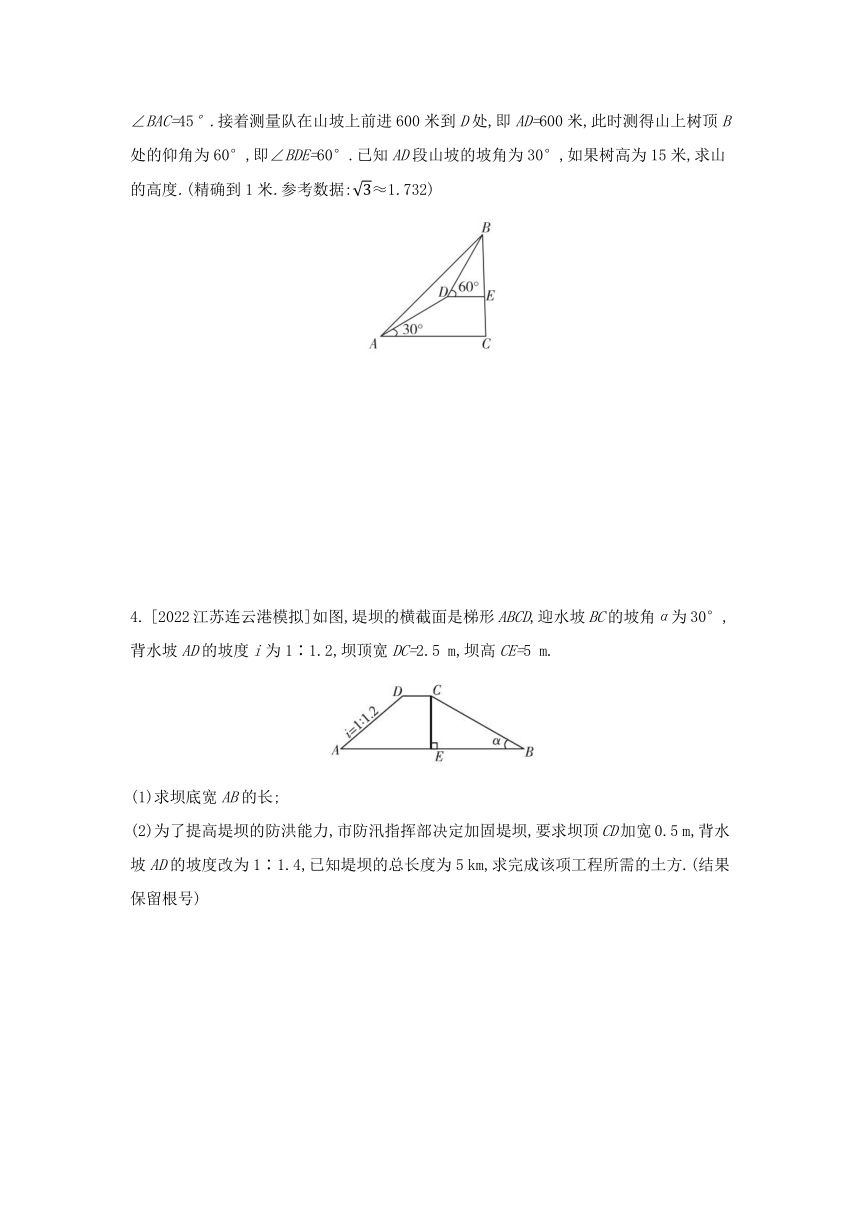
3. [2022河北九市联考]如图,某测量队在山脚A处测得山上树顶B处仰角为45°,即∠BAC=45°.接着测量队在山坡上前进600米到D处,即AD=600米,此时测得山上树顶B处的仰角为60°,即∠BDE=60°.已知AD段山坡的坡角为30°,如果树高为15米,求山的高度.(精确到1米.参考数据:≈1.732)
4. [2022江苏连云港模拟]如图,堤坝的横截面是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i为1∶1.2,坝顶宽DC=2.5 m,坝高CE=5 m.
(1)求坝底宽AB的长;
(2)为了提高堤坝的防洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽0.5 m,背水坡AD的坡度改为1∶1.4,已知堤坝的总长度为5 km,求完成该项工程所需的土方.(结果保留根号)
5. [2022河南开封模拟]“青山绿水,生态农业”.某地需引水修建水库,既可蓄水灌溉,又可美化环境.如图,水库C修建在水源A的正东方向,在水源A的北偏东75°方向有一古迹B,B与A相距14 km,其中水库C在古迹B的东南方向.
(1)若在水源A与水库C之间修建一条水渠,求该水渠的最短长度;
(2)在古迹B的西南方向5 km处有一古墓群,为了保护文物,不破坏古墓,在古墓群周围1 km范围内不得进行任何土工作业,判断按照(1)中的方式修建水渠是否合理,并说明理由.(结果保留一位小数.参考数据:sin 15°≈0.26,cos 15°≈0.97,
≈1.41)
参考答案
一、基础巩固
1.D 【解析】 连接BC.由点B在点C的北偏西55°方向上可知∠ABC=55°.在Rt△ABC中,AB==,即AB= 米.
2.10.4 【解析】 如图,过点C作CE⊥BC,过点A作BC的垂线,垂足为点F,AF的长即小岛A到航线BC的距离.根据题意可知∠DBA=60°,∠ECA=30°,∴∠ABC=30°,∠ACF
=60°,∴∠BAC=30°=∠ABC,∴AC=BC=12 n mile,∴AF=ACsin 60°=12×=6≈10.4
(n mile).
3.【解析】 (1)如图,过点P作PC⊥AB于点C,则∠PCA=∠PCB=90°.
由题意,得PA=120海里,∠A=30°,∠B=45°,
∴PC=PA=60海里,
∴PB==60 海里.
故收到求救讯息时事故渔船P与救助船B之间的距离为60 海里.
(2)∵PA=120海里,PB=60 海里,救助船A,B分别以40海里/时、30海里/时的速度同时出发,
∴救助船A所用的时间为=3(时),救助船B所用的时间为=2(时),
∵3>2,∴救助船B先到达.
4.B 【解析】 如图,过点A作AC⊥BD于点C,根据题意,得AC=60 m,AB=100 m,所以BC==80 m,所以tan α==.
5. 【解析】 由题意可知=,∴设BC=5k米,AC=12k米,∴AB===13k(米).由题意可知AB=0.5×40=20(米),∴13k=20,解得k=,∴BC=5×=(米).
6.【解析】 由题意,得AH=10米,BC=10米,
在Rt△ABC中,∠CAB=45°,∴AB=BC=10米.
在Rt△DBC中,∠CDB=30°,tan∠CDB=,
∴DB= ==10(米),
∴DH=AH-AD=AH-(DB-AB)=10-10+10≈2.7(米),
∵2.7<3,∴该建筑物需要拆除.
二、能力提升
1.B 【解析】 如图,过点D分别作AB,BC的垂线,垂足分别为点F,E,则四边形DEBF为矩形.由题意得,∠ADF=28°,CD=45 m,BC=60 m.∵山坡CD的坡度i=1∶0.75,∴=
=.设DE=4x m,则EC=3x m,在Rt△DEC中,由勾股定理可得CD=5x m.又CD=45 m,∴x=9,∴EC=3x=27 m,FB=DE=4x=36 m,∴DF=BE=BC+EC=60+27=87(m).在Rt△ADF中,AF=tan 28°×DF≈0.53×87=46.11(m),∴AB=AF+FB≈46.11+36≈82.1(m).
2.B 【解析】 根据题意,得∠CAB=65°-20°=45°,∠ACB=40°+20°=60°,AB=30 km.过点B作BE⊥AC于点E,如图所示,∴∠AEB=∠CEB=90°.在Rt△ABE中,∵∠EAB=45°,AB=30 km,∴AE=AB·cos 45°=AB=30 km,∴BE=AE=30 km.在Rt△CBE中,∵∠ECB=60°,∴CE==10 km,∴AC=AE+CE=(30+10)km,∴A,C两港之间的距离为(30+10) km.
3.【解析】 过点D作DF⊥AC于F.
在Rt△ADF中,AF=AD·cos 30°=300米,DF=AD=300米.
设FC=x米,则AC=(300+x)米.
在Rt△BDE中,BE=DE·tan 60°=DE=FC=x米,
则BC=(300+x)米.
在Rt△ACB中,∠BAC=45°,∴AC=BC,
∴300+x=300+x,解得x=300,
∴BC=(300+300)米,
∴300+300-15=285+300≈805(米),
即山的高度约为805米.
4.【解析】 (1)如图,过点D作DF⊥AB,垂足为F,
则四边形DFEC为矩形,
∴FE=DC=2.5 m,DF=CE=5 m.
∵背水坡AD的坡度i为1∶1.2,∴i==,
∴AF=1.2DF=6 m.
在Rt△CEB中,tan α=,∴BE===5 m.
∴AB=AF+FE+EB=(+5)m.
(2)如图,过点D'作D'G⊥A'B于点G,则D'G=CE=5 m,
由题意,知背水坡A'D'的坡度为1∶1.4,
∴在Rt△A'GD'中,=,∴A'G=1.4D'G=7 m.
∵CD'=0.5+2.5=3(m),∴A'B=A'G+CD'+BE=(10+5)m,
∴梯形D'A'BC的面积为×(CD'+A'B)×D'G=×(3+10+5)×5=(m2),
∴完成该项工程所需的土方为×5 000=(162 500+62 500)(m3).
5.【解析】 (1)根据“两点之间,线段最短”,可知线段AC的长即所求.
如图,过点B作BD⊥AC于点D,
由题意得∠BAD=15°,∠DBC=45°,AB=14 km.
在Rt△ADB中,BD=ABsin 15°≈3.64 km,AD=ABcos 15°≈13.58 km.
因为∠BDC=90°,∠DBC=45°,所以CD=BD≈3.64 km,
所以AC=AD+DC≈13.58+3.64≈17.2(km).
答:该水渠的最短长度约为17.2 km.
(2)不合理.理由如下:
如图,过点B作BE⊥BC交AC于点E,
由(1)知∠DCB=45°,CD≈3.64 km,
所以CE=2CD≈7.28 km,所以BE=CEsin 45°≈5.1 km.
因为5.1-5=0.1<1,
所以按照(1)中的方式修建水渠不合理.
(课时3 应用举例(2))
一、基础巩固
知识点1 方向角问题
1. [2022河北石家庄长安区二模]如图为东西流向且河岸平行的一段河道,点A,B分别为两岸上一点,且点B在点A正北方向,从点A向正东方向走a米到达点C,此时测得点B在点C的北偏西55°方向上,则河宽AB的长为 ( )
A.atan 55° 米 B. 米
C. 米 D. 米
2. 如图,海中有一个小岛A.一艘轮船由西向东航行,在B点测得小岛A在北偏东60°方向上;航行12 n mile到达C点,这时测得小岛A在北偏东30°方向上.小岛A到航线BC的距离是 n mile(≈1.73,结果用四舍五入法精确到0.1).
3. 在一次海上救援中,两艘专业救助船A,B同时收到某事故渔船P的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里.
(1)求收到求救讯息时事故渔船P与救助船B之间的距离(结果保留根号);
(2)若救助船A,B分别以40海里/时、30海里/时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.
知识点2 坡度、坡角问题
4. [2022广东广州二模]如图是一水库大坝横断面的一部分,坝高h=60 m,迎水坡AB=100 m,斜坡的坡角为α,则tan α的值为( )
A. B. C. D.
5. 太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通,如图是该地铁某站扶梯的示意图,扶梯AB的坡度i=5∶12(i为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端A以0.5米/秒的速度用时40秒到达扶梯顶端B,则王老师上升的铅直高度BC为 米.
6. 如图是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面AC的倾斜角∠CAB=45°,在距A点10米处有一建筑物HQ.为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问:该建筑物是否需要拆除 (计算最后结果保留一位小数,参考数据:≈1.414,≈1.732)
二、能力提升
1. 如图,在距某居民楼AB楼底B点左侧水平距离60 m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1∶0.75,山坡坡底C点到坡顶D点的距离CD=45 m,在坡顶D点处测得居民楼楼顶A点的仰角为28°,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为(参考数据:sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53)( )
A.76.9 m B.82.1 m C.94.8 m D.112.6 m
2. [2022安徽阜阳期末]如图,一艘船由A港沿北偏东65°方向航行30 km至B港,然后沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为( )
A.(30+30) km B.(30+10) km
C.(10+30) km D.30 km
3. [2022河北九市联考]如图,某测量队在山脚A处测得山上树顶B处仰角为45°,即∠BAC=45°.接着测量队在山坡上前进600米到D处,即AD=600米,此时测得山上树顶B处的仰角为60°,即∠BDE=60°.已知AD段山坡的坡角为30°,如果树高为15米,求山的高度.(精确到1米.参考数据:≈1.732)
4. [2022江苏连云港模拟]如图,堤坝的横截面是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i为1∶1.2,坝顶宽DC=2.5 m,坝高CE=5 m.
(1)求坝底宽AB的长;
(2)为了提高堤坝的防洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽0.5 m,背水坡AD的坡度改为1∶1.4,已知堤坝的总长度为5 km,求完成该项工程所需的土方.(结果保留根号)
5. [2022河南开封模拟]“青山绿水,生态农业”.某地需引水修建水库,既可蓄水灌溉,又可美化环境.如图,水库C修建在水源A的正东方向,在水源A的北偏东75°方向有一古迹B,B与A相距14 km,其中水库C在古迹B的东南方向.
(1)若在水源A与水库C之间修建一条水渠,求该水渠的最短长度;
(2)在古迹B的西南方向5 km处有一古墓群,为了保护文物,不破坏古墓,在古墓群周围1 km范围内不得进行任何土工作业,判断按照(1)中的方式修建水渠是否合理,并说明理由.(结果保留一位小数.参考数据:sin 15°≈0.26,cos 15°≈0.97,
≈1.41)
参考答案
一、基础巩固
1.D 【解析】 连接BC.由点B在点C的北偏西55°方向上可知∠ABC=55°.在Rt△ABC中,AB==,即AB= 米.
2.10.4 【解析】 如图,过点C作CE⊥BC,过点A作BC的垂线,垂足为点F,AF的长即小岛A到航线BC的距离.根据题意可知∠DBA=60°,∠ECA=30°,∴∠ABC=30°,∠ACF
=60°,∴∠BAC=30°=∠ABC,∴AC=BC=12 n mile,∴AF=ACsin 60°=12×=6≈10.4
(n mile).
3.【解析】 (1)如图,过点P作PC⊥AB于点C,则∠PCA=∠PCB=90°.
由题意,得PA=120海里,∠A=30°,∠B=45°,
∴PC=PA=60海里,
∴PB==60 海里.
故收到求救讯息时事故渔船P与救助船B之间的距离为60 海里.
(2)∵PA=120海里,PB=60 海里,救助船A,B分别以40海里/时、30海里/时的速度同时出发,
∴救助船A所用的时间为=3(时),救助船B所用的时间为=2(时),
∵3>2,∴救助船B先到达.
4.B 【解析】 如图,过点A作AC⊥BD于点C,根据题意,得AC=60 m,AB=100 m,所以BC==80 m,所以tan α==.
5. 【解析】 由题意可知=,∴设BC=5k米,AC=12k米,∴AB===13k(米).由题意可知AB=0.5×40=20(米),∴13k=20,解得k=,∴BC=5×=(米).
6.【解析】 由题意,得AH=10米,BC=10米,
在Rt△ABC中,∠CAB=45°,∴AB=BC=10米.
在Rt△DBC中,∠CDB=30°,tan∠CDB=,
∴DB= ==10(米),
∴DH=AH-AD=AH-(DB-AB)=10-10+10≈2.7(米),
∵2.7<3,∴该建筑物需要拆除.
二、能力提升
1.B 【解析】 如图,过点D分别作AB,BC的垂线,垂足分别为点F,E,则四边形DEBF为矩形.由题意得,∠ADF=28°,CD=45 m,BC=60 m.∵山坡CD的坡度i=1∶0.75,∴=
=.设DE=4x m,则EC=3x m,在Rt△DEC中,由勾股定理可得CD=5x m.又CD=45 m,∴x=9,∴EC=3x=27 m,FB=DE=4x=36 m,∴DF=BE=BC+EC=60+27=87(m).在Rt△ADF中,AF=tan 28°×DF≈0.53×87=46.11(m),∴AB=AF+FB≈46.11+36≈82.1(m).
2.B 【解析】 根据题意,得∠CAB=65°-20°=45°,∠ACB=40°+20°=60°,AB=30 km.过点B作BE⊥AC于点E,如图所示,∴∠AEB=∠CEB=90°.在Rt△ABE中,∵∠EAB=45°,AB=30 km,∴AE=AB·cos 45°=AB=30 km,∴BE=AE=30 km.在Rt△CBE中,∵∠ECB=60°,∴CE==10 km,∴AC=AE+CE=(30+10)km,∴A,C两港之间的距离为(30+10) km.
3.【解析】 过点D作DF⊥AC于F.
在Rt△ADF中,AF=AD·cos 30°=300米,DF=AD=300米.
设FC=x米,则AC=(300+x)米.
在Rt△BDE中,BE=DE·tan 60°=DE=FC=x米,
则BC=(300+x)米.
在Rt△ACB中,∠BAC=45°,∴AC=BC,
∴300+x=300+x,解得x=300,
∴BC=(300+300)米,
∴300+300-15=285+300≈805(米),
即山的高度约为805米.
4.【解析】 (1)如图,过点D作DF⊥AB,垂足为F,
则四边形DFEC为矩形,
∴FE=DC=2.5 m,DF=CE=5 m.
∵背水坡AD的坡度i为1∶1.2,∴i==,
∴AF=1.2DF=6 m.
在Rt△CEB中,tan α=,∴BE===5 m.
∴AB=AF+FE+EB=(+5)m.
(2)如图,过点D'作D'G⊥A'B于点G,则D'G=CE=5 m,
由题意,知背水坡A'D'的坡度为1∶1.4,
∴在Rt△A'GD'中,=,∴A'G=1.4D'G=7 m.
∵CD'=0.5+2.5=3(m),∴A'B=A'G+CD'+BE=(10+5)m,
∴梯形D'A'BC的面积为×(CD'+A'B)×D'G=×(3+10+5)×5=(m2),
∴完成该项工程所需的土方为×5 000=(162 500+62 500)(m3).
5.【解析】 (1)根据“两点之间,线段最短”,可知线段AC的长即所求.
如图,过点B作BD⊥AC于点D,
由题意得∠BAD=15°,∠DBC=45°,AB=14 km.
在Rt△ADB中,BD=ABsin 15°≈3.64 km,AD=ABcos 15°≈13.58 km.
因为∠BDC=90°,∠DBC=45°,所以CD=BD≈3.64 km,
所以AC=AD+DC≈13.58+3.64≈17.2(km).
答:该水渠的最短长度约为17.2 km.
(2)不合理.理由如下:
如图,过点B作BE⊥BC交AC于点E,
由(1)知∠DCB=45°,CD≈3.64 km,
所以CE=2CD≈7.28 km,所以BE=CEsin 45°≈5.1 km.
因为5.1-5=0.1<1,
所以按照(1)中的方式修建水渠不合理.
