第二十七章 相似全章综合测试题 人教版数学九年级下册(含解析)
文档属性
| 名称 | 第二十七章 相似全章综合测试题 人教版数学九年级下册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 354.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 00:00:00 | ||
图片预览


文档简介
《第二十七章 相似》全章综合测试题
一、选择题
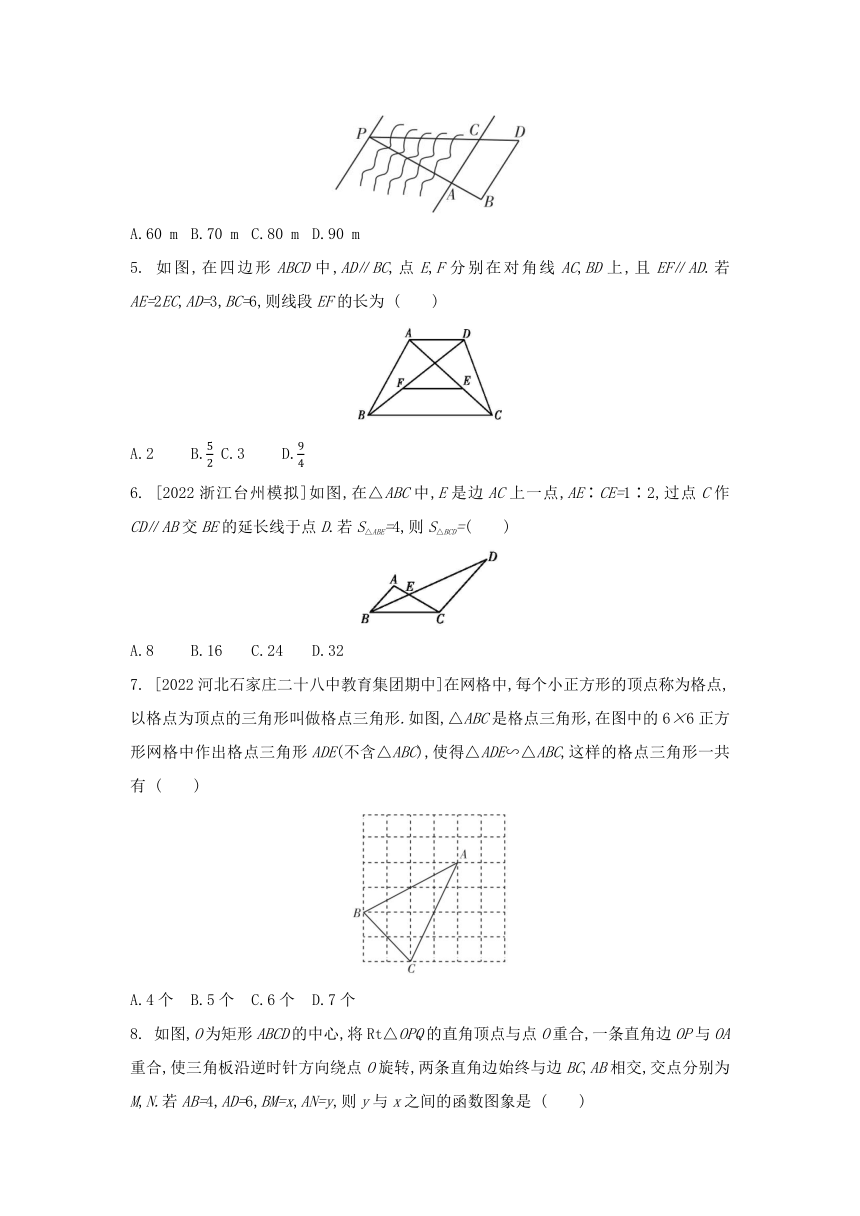
1. [2022安徽合肥包河区期中]勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉,生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2 m,则a约为( )
A.1.23 m B.1.24 m C.1.25 m D.1.26 m
2. [2022上海徐汇区一模]如图,AB∥CD∥FF,AC=2,AE=5,BD=,那么下列结论正确的是( )
A.DF= B.EF= C.CD= D.BF=
3. 如图,已知△ABC的六个元素,其中a,b,c表示三角形三边的长,则下面甲、乙、丙、丁四个三角形中与△ABC不一定相似的图形是 ( )
A.甲 B.乙 C.丙 D.丁
4. 如图,为了确定一条河的宽度,测量人员先观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条与河岸垂直的直线上,随后确定点C和点D,使AC⊥BP,BD⊥BP,点C为AC与DP的交点.他们测得AB=20 m,AC=40 m,BD=50 m,从而确定河宽PA为 ( )
A.60 m B.70 m C.80 m D.90 m
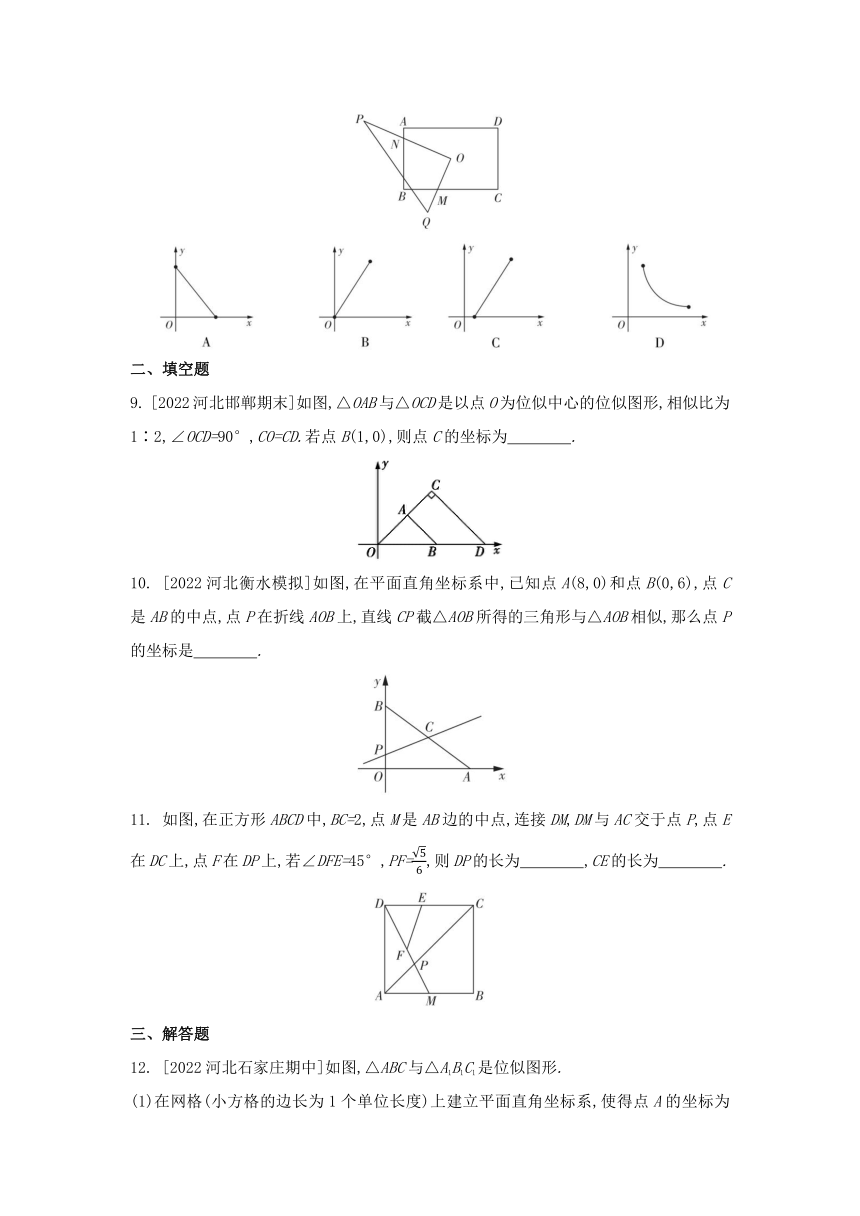
5. 如图,在四边形ABCD中,AD∥BC,点E,F分别在对角线AC,BD上,且EF∥AD.若AE=2EC,AD=3,BC=6,则线段EF的长为 ( )
A.2 B. C.3 D.
6. [2022浙江台州模拟]如图,在△ABC中,E是边AC上一点,AE∶CE=1∶2,过点C作CD∥AB交BE的延长线于点D.若S△ABE=4,则S△BCD=( )
A.8 B.16 C.24 D.32
7. [2022河北石家庄二十八中教育集团期中]在网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形ADE(不含△ABC),使得△ADE∽△ABC,这样的格点三角形一共有 ( )
A.4个 B.5个 C.6个 D.7个
8. 如图,O为矩形ABCD的中心,将Rt△OPQ的直角顶点与点O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC,AB相交,交点分别为M,N.若AB=4,AD=6,BM=x,AN=y,则y与x之间的函数图象是 ( )
二、填空题
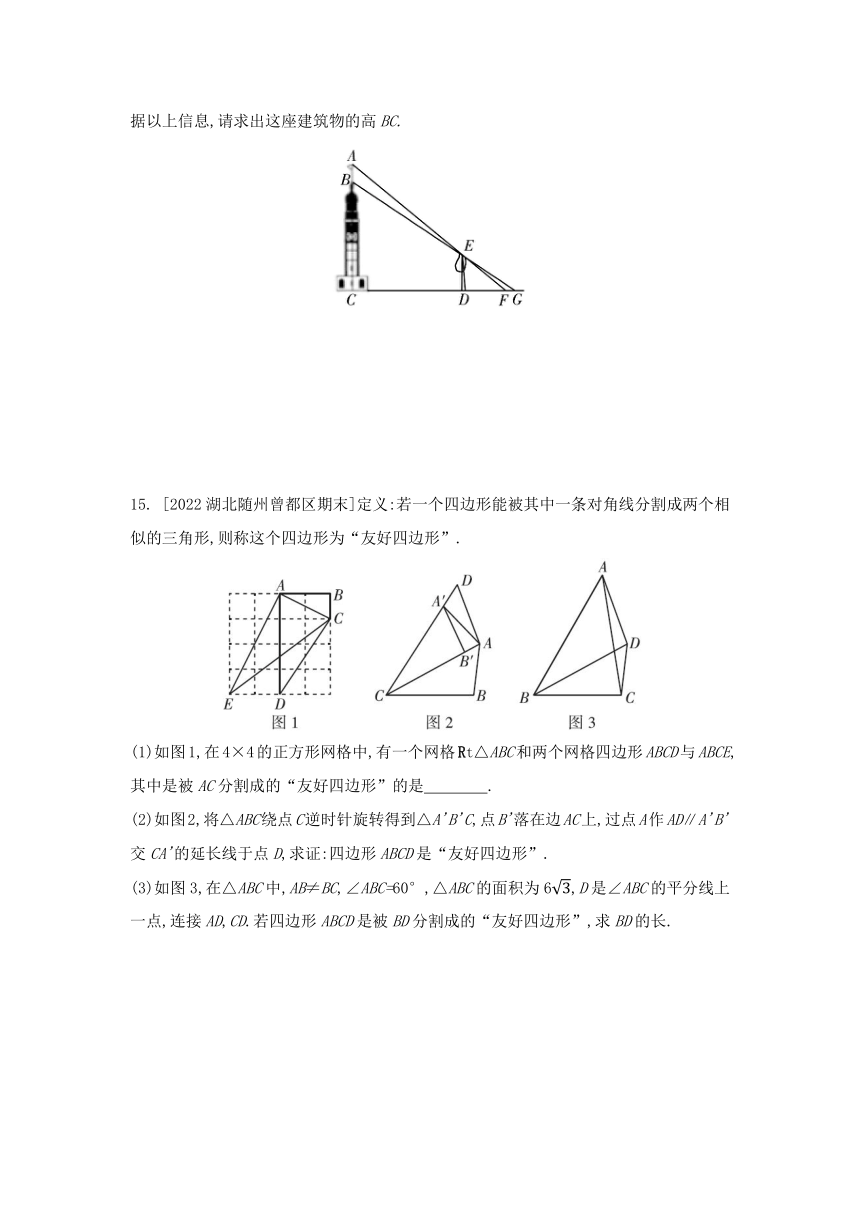
9. [2022河北邯郸期末]如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD.若点B(1,0),则点C的坐标为 .
10. [2022河北衡水模拟]如图,在平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB所得的三角形与△AOB相似,那么点P的坐标是 .
11. 如图,在正方形ABCD中,BC=2,点M是AB边的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,若∠DFE=45°,PF=,则DP的长为 ,CE的长为 .
三、解答题
12. [2022河北石家庄期中]如图,△ABC与△A1B1C1是位似图形.
(1)在网格(小方格的边长为1个单位长度)上建立平面直角坐标系,使得点A的坐标为(-6,-1),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且相似比为1∶2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .
13. [2022上海普陀区二模]如图,在 ABCD中,点E,F分别在边BC、边BC的延长线上,四边形AEFD是菱形,菱形的对角线AF分别交DE,DC于点P,Q,=.
求证:(1)四边形ABCD为矩形;
(2)BE·DQ=FQ·PE.
14. [2022河北石家庄二十七中期中]如图,建筑物BC上有一个旗杆AB,小明和数学兴趣小组的同学计划用学过的知识测量该建筑物的高度.他们制订了测量方案,并利用课余时间完成了实地测量,测量方法如下:在该建筑物底部所在的平地上有一棵小树ED,小明沿CD后退,发现地面上的点F、树顶E、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶E、建筑物顶端B恰好在一条直线上.已知旗杆AB=3米,DE=4米,DF=5米,FG=1.5米,点A,B,C在一条直线上,点C,D,F,G在一条直线上,AC,ED均垂直于CG,根据以上信息,请求出这座建筑物的高BC.
15. [2022湖北随州曾都区期末]定义:若一个四边形能被其中一条对角线分割成两个相似的三角形,则称这个四边形为“友好四边形”.
(1)如图1,在4×4的正方形网格中,有一个网格Rt△ABC和两个网格四边形ABCD与ABCE,其中是被AC分割成的“友好四边形”的是 .
(2)如图2,将△ABC绕点C逆时针旋转得到△A'B'C,点B'落在边AC上,过点A作AD∥A'B'交CA'的延长线于点D,求证:四边形ABCD是“友好四边形”.
(3)如图3,在△ABC中,AB≠BC,∠ABC=60°,△ABC的面积为6,D是∠ABC的平分线上一点,连接AD,CD.若四边形ABCD是被BD分割成的“友好四边形”,求BD的长.
参考答案
一、选择题
1.B 【解析】 根据题意,得≈0.618,所以a≈0.618b≈1.24 m.
2.D 【解析】 ∵AB∥CD∥FF,∴=,∵AC=2,AE=5,BD=,∴=,∴DF=,
∴BF=BD+DF==.
3.A 【解析】 三角形甲的两边DF,EF的夹角不一定等于72°,故此三角形与△ABC不一定相似;利用“两边成比例且夹角相等的两个三角形相似”,可得三角形乙与△ABC相似;利用“两角分别相等的两个三角形相似”,可得丙、丁两个三角形与△ABC相似.故与△ABC不一定相似的图形是甲.
4.C 【解析】 ∵AC⊥BP,BD⊥BP,∴AC∥BD,∴△PBD∽△PAC,∴=.∵AB=20 m,AC=40 m,BD=50 m,∴=,∴PA=80 m.
5.C 【解析】 解法一 如图,延长EF交AB于点G.易证△AGE∽△ABC,△BGF∽△BAD,∴===,==,∴GE=BC=4,GF=AD=1,∴EF=GE-GF=4-1=3.
解法二 设AC与BD相交于点H.由AD∥BC,AD∥EF,可得△AHD∽△EHF∽△CHB,
∴===,∴AH=AC.∵AE=2EC,∴EC=AC=AH,∴HE=AC,∴AH=HE,∴△AHD≌△EHF,∴EF=AD=3.
6.C 【解析】 ∵CD∥AB,∴△ABE∽△CDE.∵AE∶CE=1∶2,∴S△ABE∶S△CDE=1∶4.∵S△ABE=4,
∴S△CDE=16.∵AE∶CE=1∶2,∴CE=2AE,∴S△BCE=2S△ABE=8,∴S△BCD=S△CDE+S△BCE=16+8=24.
7.C 【解析】 如图,使得△ADE∽△ABC的格点三角形一共有6个.
8.C 【解析】 如图,过点O分别作OF⊥AB于点F,OE⊥BC于点E,∵∠POQ=∠EOF=90°,
∴∠NOF=∠MOE,又∠NFO=∠MEO=90°,∴△NOF∽△MOE,∴=.∵AB=4,AD=6,BM=x,
AN=y,∴NF=2-y,ME=3-x,OF=3,OE=2,∴=,∴y=x-.∵0≤y≤4,∴0≤x-≤4,∴≤x≤,∴y=x-(≤x≤),故C项中的图象符合题意.
二、填空题
9.(1,1) 【解析】 由题意,得△OAB与△OCD是等腰直角三角形,BO=1,∴AO=AB=,∴A(,),∵△OAB∽△OCD,且相似比为1∶2,∴点C的坐标为(1,1).
10.(0,3)或(4,0)或(,0) 【解析】 当PC∥OA时,△BPC∽△BOA,由点C是AB的中点,可得P为OB的中点.∵点B的坐标为(0,6),∴点P的坐标为(0,3).当PC∥OB时,△ACP∽△ABO,由点C是AB的中点,可得P为OA的中点.∵点A的坐标为(8,0),∴点P的坐标为(4,0).当PC⊥AB时,如图,∵∠CAP=∠OAB,∴Rt△APC∽Rt△ABO,∴=.
∵A(8,0),B(0,6),∴AB==10.∵点C是AB的中点,∴AC=5,∴=,∴AP=,
∴OP=OA-AP=8-=,∴点P的坐标为(,0).综上,点P的坐标为(0,3)或(4,0)或(,0).
11. 【解析】 ∵四边形ABCD是正方形,∴AB=BC=CD=DA=2,∠DAB=90°,
∠DCP=45°.∵点M是AB边的中点,∴AM=BM=1.在Rt△ADM中,DM==.
∵AM∥CD,∴△AMP∽△CDP,∴==,∴DP=.∵PF=,∴DF=DP-PF=-=.∵∠EDF=∠PDC,∠DFE=∠DCP=45°,∴△DEF∽△DPC,∴=,即=,∴DE=,∴CE=CD-DE=2-=.
三、解答题
12.【解析】 (1)建立平面直角坐标系如图所示.
(-2,-5)
(2)△AB2C2如图所示.
(3)点P如图所示.
(-2,1) 6+4
四边形ABCP的周长为+++=4+2+2+2
=6+4.
13.【解析】 (1)∵四边形AEFD是菱形,
∴AF⊥DE,∴∠EPF=90°.
∵=,∠AFB=∠PFE,
∴△ABF∽△EPF,∴∠ABE=∠EPF=90°,
∴平行四边形ABCD是矩形.
(2)∵四边形ABCD是矩形,
∴AD=BC=EF,∴BE=CF.
∵∠DPF=∠QCF=90°,∠CQF=∠PQD,
∴△DPQ∽△FCQ,∴=,
∴=,∴BE·DQ=FQ·PE.
14.【解析】 由题意可得,∠ACF=∠EDF=90°,∠AFC=∠EFD,
∴△ACF∽△EDF,∴=,
即=,∴CD=.
由题意可得,∠BCG=∠EDG=90°,∠BGC=∠EGD,
∴△BCG∽△EDG,∴=,
即=,∴CD=,
∴=,∴BC=14,
∴这座建筑物的高BC为14米.
16.【解析】 (1)四边形ABCE
设正方形网格中每个小正方形的边长均为1,则AB=2,BC=1,AD=4,AC==,CD==,AE==2,CE==5,∴===,∴△ABC∽△EAC,∴四边形ABCE是“友好四边形”.∵≠,∴△ABC与△DCA不相似,∴四边形ABCD不是“友好四边形”.
(2)根据旋转的性质,得∠A'CB'=∠ACB,∠CA'B'=∠CAB.
∵AD∥A'B',∴∠CA'B'=∠D,∴∠CAB=∠D,
又∠DCA=∠ACB,∴△ABC∽△DAC,
∴四边形ABCD是“友好四边形”.
(3)如图,过点A作AM⊥BC于点M.
在Rt△ABM中,∠ABM=60°,
∴∠BAM=30°,
∴BM=AB,∴AM=AB.
∵△ABC的面积为6,
∴BC×AB=6,∴BC×AB=24.
∵BD是∠ABC的平分线,∴∠ABD=∠DBC.
∵四边形ABCD是被BD分割成的“友好四边形”,且AB≠BC,
∴△ABD∽△DBC,∴=,
∴BD2=AB×BC=24,∴BD==2.
一、选择题
1. [2022安徽合肥包河区期中]勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉,生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2 m,则a约为( )
A.1.23 m B.1.24 m C.1.25 m D.1.26 m
2. [2022上海徐汇区一模]如图,AB∥CD∥FF,AC=2,AE=5,BD=,那么下列结论正确的是( )
A.DF= B.EF= C.CD= D.BF=
3. 如图,已知△ABC的六个元素,其中a,b,c表示三角形三边的长,则下面甲、乙、丙、丁四个三角形中与△ABC不一定相似的图形是 ( )
A.甲 B.乙 C.丙 D.丁
4. 如图,为了确定一条河的宽度,测量人员先观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条与河岸垂直的直线上,随后确定点C和点D,使AC⊥BP,BD⊥BP,点C为AC与DP的交点.他们测得AB=20 m,AC=40 m,BD=50 m,从而确定河宽PA为 ( )
A.60 m B.70 m C.80 m D.90 m
5. 如图,在四边形ABCD中,AD∥BC,点E,F分别在对角线AC,BD上,且EF∥AD.若AE=2EC,AD=3,BC=6,则线段EF的长为 ( )
A.2 B. C.3 D.
6. [2022浙江台州模拟]如图,在△ABC中,E是边AC上一点,AE∶CE=1∶2,过点C作CD∥AB交BE的延长线于点D.若S△ABE=4,则S△BCD=( )
A.8 B.16 C.24 D.32
7. [2022河北石家庄二十八中教育集团期中]在网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形ADE(不含△ABC),使得△ADE∽△ABC,这样的格点三角形一共有 ( )
A.4个 B.5个 C.6个 D.7个
8. 如图,O为矩形ABCD的中心,将Rt△OPQ的直角顶点与点O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC,AB相交,交点分别为M,N.若AB=4,AD=6,BM=x,AN=y,则y与x之间的函数图象是 ( )
二、填空题
9. [2022河北邯郸期末]如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD.若点B(1,0),则点C的坐标为 .
10. [2022河北衡水模拟]如图,在平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB所得的三角形与△AOB相似,那么点P的坐标是 .
11. 如图,在正方形ABCD中,BC=2,点M是AB边的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,若∠DFE=45°,PF=,则DP的长为 ,CE的长为 .
三、解答题
12. [2022河北石家庄期中]如图,△ABC与△A1B1C1是位似图形.
(1)在网格(小方格的边长为1个单位长度)上建立平面直角坐标系,使得点A的坐标为(-6,-1),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且相似比为1∶2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .
13. [2022上海普陀区二模]如图,在 ABCD中,点E,F分别在边BC、边BC的延长线上,四边形AEFD是菱形,菱形的对角线AF分别交DE,DC于点P,Q,=.
求证:(1)四边形ABCD为矩形;
(2)BE·DQ=FQ·PE.
14. [2022河北石家庄二十七中期中]如图,建筑物BC上有一个旗杆AB,小明和数学兴趣小组的同学计划用学过的知识测量该建筑物的高度.他们制订了测量方案,并利用课余时间完成了实地测量,测量方法如下:在该建筑物底部所在的平地上有一棵小树ED,小明沿CD后退,发现地面上的点F、树顶E、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶E、建筑物顶端B恰好在一条直线上.已知旗杆AB=3米,DE=4米,DF=5米,FG=1.5米,点A,B,C在一条直线上,点C,D,F,G在一条直线上,AC,ED均垂直于CG,根据以上信息,请求出这座建筑物的高BC.
15. [2022湖北随州曾都区期末]定义:若一个四边形能被其中一条对角线分割成两个相似的三角形,则称这个四边形为“友好四边形”.
(1)如图1,在4×4的正方形网格中,有一个网格Rt△ABC和两个网格四边形ABCD与ABCE,其中是被AC分割成的“友好四边形”的是 .
(2)如图2,将△ABC绕点C逆时针旋转得到△A'B'C,点B'落在边AC上,过点A作AD∥A'B'交CA'的延长线于点D,求证:四边形ABCD是“友好四边形”.
(3)如图3,在△ABC中,AB≠BC,∠ABC=60°,△ABC的面积为6,D是∠ABC的平分线上一点,连接AD,CD.若四边形ABCD是被BD分割成的“友好四边形”,求BD的长.
参考答案
一、选择题
1.B 【解析】 根据题意,得≈0.618,所以a≈0.618b≈1.24 m.
2.D 【解析】 ∵AB∥CD∥FF,∴=,∵AC=2,AE=5,BD=,∴=,∴DF=,
∴BF=BD+DF==.
3.A 【解析】 三角形甲的两边DF,EF的夹角不一定等于72°,故此三角形与△ABC不一定相似;利用“两边成比例且夹角相等的两个三角形相似”,可得三角形乙与△ABC相似;利用“两角分别相等的两个三角形相似”,可得丙、丁两个三角形与△ABC相似.故与△ABC不一定相似的图形是甲.
4.C 【解析】 ∵AC⊥BP,BD⊥BP,∴AC∥BD,∴△PBD∽△PAC,∴=.∵AB=20 m,AC=40 m,BD=50 m,∴=,∴PA=80 m.
5.C 【解析】 解法一 如图,延长EF交AB于点G.易证△AGE∽△ABC,△BGF∽△BAD,∴===,==,∴GE=BC=4,GF=AD=1,∴EF=GE-GF=4-1=3.
解法二 设AC与BD相交于点H.由AD∥BC,AD∥EF,可得△AHD∽△EHF∽△CHB,
∴===,∴AH=AC.∵AE=2EC,∴EC=AC=AH,∴HE=AC,∴AH=HE,∴△AHD≌△EHF,∴EF=AD=3.
6.C 【解析】 ∵CD∥AB,∴△ABE∽△CDE.∵AE∶CE=1∶2,∴S△ABE∶S△CDE=1∶4.∵S△ABE=4,
∴S△CDE=16.∵AE∶CE=1∶2,∴CE=2AE,∴S△BCE=2S△ABE=8,∴S△BCD=S△CDE+S△BCE=16+8=24.
7.C 【解析】 如图,使得△ADE∽△ABC的格点三角形一共有6个.
8.C 【解析】 如图,过点O分别作OF⊥AB于点F,OE⊥BC于点E,∵∠POQ=∠EOF=90°,
∴∠NOF=∠MOE,又∠NFO=∠MEO=90°,∴△NOF∽△MOE,∴=.∵AB=4,AD=6,BM=x,
AN=y,∴NF=2-y,ME=3-x,OF=3,OE=2,∴=,∴y=x-.∵0≤y≤4,∴0≤x-≤4,∴≤x≤,∴y=x-(≤x≤),故C项中的图象符合题意.
二、填空题
9.(1,1) 【解析】 由题意,得△OAB与△OCD是等腰直角三角形,BO=1,∴AO=AB=,∴A(,),∵△OAB∽△OCD,且相似比为1∶2,∴点C的坐标为(1,1).
10.(0,3)或(4,0)或(,0) 【解析】 当PC∥OA时,△BPC∽△BOA,由点C是AB的中点,可得P为OB的中点.∵点B的坐标为(0,6),∴点P的坐标为(0,3).当PC∥OB时,△ACP∽△ABO,由点C是AB的中点,可得P为OA的中点.∵点A的坐标为(8,0),∴点P的坐标为(4,0).当PC⊥AB时,如图,∵∠CAP=∠OAB,∴Rt△APC∽Rt△ABO,∴=.
∵A(8,0),B(0,6),∴AB==10.∵点C是AB的中点,∴AC=5,∴=,∴AP=,
∴OP=OA-AP=8-=,∴点P的坐标为(,0).综上,点P的坐标为(0,3)或(4,0)或(,0).
11. 【解析】 ∵四边形ABCD是正方形,∴AB=BC=CD=DA=2,∠DAB=90°,
∠DCP=45°.∵点M是AB边的中点,∴AM=BM=1.在Rt△ADM中,DM==.
∵AM∥CD,∴△AMP∽△CDP,∴==,∴DP=.∵PF=,∴DF=DP-PF=-=.∵∠EDF=∠PDC,∠DFE=∠DCP=45°,∴△DEF∽△DPC,∴=,即=,∴DE=,∴CE=CD-DE=2-=.
三、解答题
12.【解析】 (1)建立平面直角坐标系如图所示.
(-2,-5)
(2)△AB2C2如图所示.
(3)点P如图所示.
(-2,1) 6+4
四边形ABCP的周长为+++=4+2+2+2
=6+4.
13.【解析】 (1)∵四边形AEFD是菱形,
∴AF⊥DE,∴∠EPF=90°.
∵=,∠AFB=∠PFE,
∴△ABF∽△EPF,∴∠ABE=∠EPF=90°,
∴平行四边形ABCD是矩形.
(2)∵四边形ABCD是矩形,
∴AD=BC=EF,∴BE=CF.
∵∠DPF=∠QCF=90°,∠CQF=∠PQD,
∴△DPQ∽△FCQ,∴=,
∴=,∴BE·DQ=FQ·PE.
14.【解析】 由题意可得,∠ACF=∠EDF=90°,∠AFC=∠EFD,
∴△ACF∽△EDF,∴=,
即=,∴CD=.
由题意可得,∠BCG=∠EDG=90°,∠BGC=∠EGD,
∴△BCG∽△EDG,∴=,
即=,∴CD=,
∴=,∴BC=14,
∴这座建筑物的高BC为14米.
16.【解析】 (1)四边形ABCE
设正方形网格中每个小正方形的边长均为1,则AB=2,BC=1,AD=4,AC==,CD==,AE==2,CE==5,∴===,∴△ABC∽△EAC,∴四边形ABCE是“友好四边形”.∵≠,∴△ABC与△DCA不相似,∴四边形ABCD不是“友好四边形”.
(2)根据旋转的性质,得∠A'CB'=∠ACB,∠CA'B'=∠CAB.
∵AD∥A'B',∴∠CA'B'=∠D,∴∠CAB=∠D,
又∠DCA=∠ACB,∴△ABC∽△DAC,
∴四边形ABCD是“友好四边形”.
(3)如图,过点A作AM⊥BC于点M.
在Rt△ABM中,∠ABM=60°,
∴∠BAM=30°,
∴BM=AB,∴AM=AB.
∵△ABC的面积为6,
∴BC×AB=6,∴BC×AB=24.
∵BD是∠ABC的平分线,∴∠ABD=∠DBC.
∵四边形ABCD是被BD分割成的“友好四边形”,且AB≠BC,
∴△ABD∽△DBC,∴=,
∴BD2=AB×BC=24,∴BD==2.
