2.1等式性质和不等式性质(第2课时)课件-2023-2024学年高一上学期数学人教A版(2019)必修第一册(共23张PPT)
文档属性
| 名称 | 2.1等式性质和不等式性质(第2课时)课件-2023-2024学年高一上学期数学人教A版(2019)必修第一册(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 69.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 14:57:52 | ||
图片预览








文档简介
(共23张PPT)
NEW
2023 / 07
第 2 章 一元二次函数、方程和不等式
人教A版2019必修第一册
2.1 等式性质与不等式性质
学习目标
1. 掌握等式性质与不等式性质以及推论,能够运用其解决简单的问题.
2. 进一步掌握作差、作商、综合法等比较法比较实数的大小.
3.掌握并会应用重要不等式.
4. 通过教学培养学生合作交流的意识和大胆猜测、乐于探究的良好思维品质。
Topic. 01
01 情景导入
复习导入
等式有下面的基本性质:
性质1 如果=b,那么b=;
性质2 如果=b,b=c,那么=c;
性质3 如果=b,那么±c=b±c;
性质4 如果=b,那么c=bc;
性质5 如果=b,c≠0,那么
等式的性质
对称性
传递性
加减性
同乘性
同除性
类比等式的基本性质,你能猜想不等式的基本性质吗?
Topic. 02
02 不等关系性质
不等式性质
探究1:对称性
证明:∵a>b,∴a-b>0.
由正数的相反数是负数,得-(a-b)<0.
即b-a<0,∴b同理可证,如果bb.
如果,那么.即
1.与m≥(n-2)2等价的是( ).
A.m<(n-2)2 B.(n-2)2≥m
C.(n-2)2≤m D.(n-2)2不等式性质
C
不等式性质
探究2:传递性
蝴蝶效应
如果,,那么.即,
证明:
不等式性质
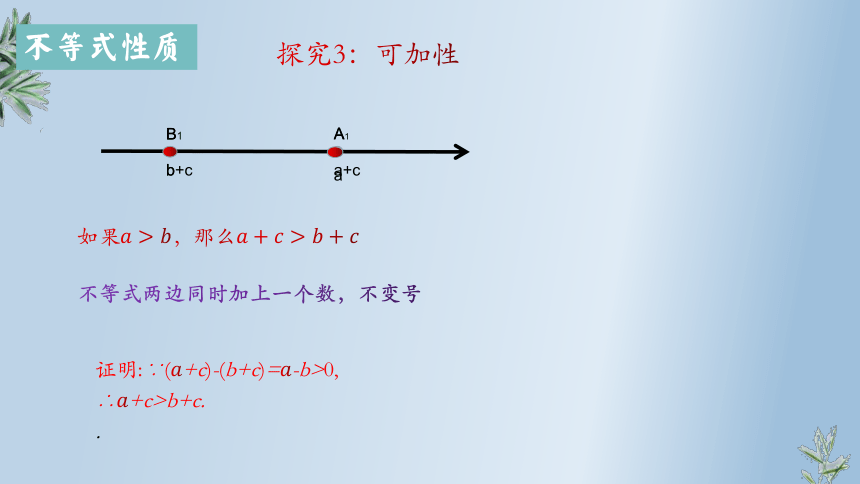
探究3:可加性
如果,那么
不等式两边同时加上一个数,不变号
A
a
A1
a+c
B
b
B1
b+c
证明:∵(+c)-(b+c)=-b>0,
∴+c>b+c.
.
不等式性质
探究4:可乘性
如果,,那么;
不等式两边同时乘上一个正数,不变号;
证明:ac-bc=(a-b)c.∵a>b,∴a-b>0.
根据同号相乘得正,异号相乘得负,
得当c>0时,(a-b)c>0,即ac>bc;
当c<0时,(a-b)c<0,即ac1. 该性质不能逆推,如c>bc >b.
2.c>bc >b,c>0或a3.不等式两边仅能同乘(或除以)一 个符号确定的非零实数.
注意:
如果,,那么
不等式两边同时乘上一个负数,要变号 .
不等式性质
探究5:同向可加性
如果,,那么
如果,,那么
如果,,那么
探究6:同向同正可乘性
如果, ,那么
探究7:同正可乘方性
如果,那么
不等式性质
(1)对称性:a>b .(2)传递性:a>b,b>c .(3)可加性:a>b .(4)可乘性:a>b,c>0 ;a>b,c<0 .(5)加法法则:a>b,c>d .(6)乘法法则:a>b>0,c>d>0 .(7)乘方法则:a>b>0 _____________________.
Topic. 03
03 不等式性质应用
[思路点拨] 本题可以利用不等式的性质直接判断命题的真假,也可以采用特殊值法判断.
D
不等式性质的应用
.
不等式性质的应用
不等式性质的应用
不等式性质的应用
证明:
不等式性质应用
3.若a>b,c>d,则下列不等关系中不一定成立的是( )A.a-b>d-c B.a+d>b+cC.a-c>b-c D.a-c<a-d
B
不等式性质的应用
4.与a>b等价的不等式是( )A.|a|>|b| B.a2>b2C.>1 D.a3>b3
D
不等式性质的应用
5.已知实数满足,,求,的取值范围;
解:
注意:
同向不等式具有可加性与可乘性(同正),但是不具有可减性与可除性,应用时要充分利用所给条件进行适当变形来求取值范围,注意变形的等价性。
不等式性质的应用
6.已知实数满足,,求的取值范围。
解:设
则,解得
即
,
Topic. 04
04 课堂小结
课堂小结
(1)对称性:a>b .
(2)传递性:a>b,b>c .
(3)可加性:a>b .
(4)可乘性:a>b,c>0 ;a>b,c<0 .
(5)加法法则:a>b,c>d .
(6)乘法法则:a>b>0,c>d>0 .
(7)乘方法则:a>b>0 _____________________.
NEW
2023 / 07
第 2 章 一元二次函数、方程和不等式
人教A版2019必修第一册
2.1 等式性质与不等式性质
学习目标
1. 掌握等式性质与不等式性质以及推论,能够运用其解决简单的问题.
2. 进一步掌握作差、作商、综合法等比较法比较实数的大小.
3.掌握并会应用重要不等式.
4. 通过教学培养学生合作交流的意识和大胆猜测、乐于探究的良好思维品质。
Topic. 01
01 情景导入
复习导入
等式有下面的基本性质:
性质1 如果=b,那么b=;
性质2 如果=b,b=c,那么=c;
性质3 如果=b,那么±c=b±c;
性质4 如果=b,那么c=bc;
性质5 如果=b,c≠0,那么
等式的性质
对称性
传递性
加减性
同乘性
同除性
类比等式的基本性质,你能猜想不等式的基本性质吗?
Topic. 02
02 不等关系性质
不等式性质
探究1:对称性
证明:∵a>b,∴a-b>0.
由正数的相反数是负数,得-(a-b)<0.
即b-a<0,∴b
如果,那么.即
1.与m≥(n-2)2等价的是( ).
A.m<(n-2)2 B.(n-2)2≥m
C.(n-2)2≤m D.(n-2)2
C
不等式性质
探究2:传递性
蝴蝶效应
如果,,那么.即,
证明:
不等式性质
探究3:可加性
如果,那么
不等式两边同时加上一个数,不变号
A
a
A1
a+c
B
b
B1
b+c
证明:∵(+c)-(b+c)=-b>0,
∴+c>b+c.
.
不等式性质
探究4:可乘性
如果,,那么;
不等式两边同时乘上一个正数,不变号;
证明:ac-bc=(a-b)c.∵a>b,∴a-b>0.
根据同号相乘得正,异号相乘得负,
得当c>0时,(a-b)c>0,即ac>bc;
当c<0时,(a-b)c<0,即ac
2.c>bc >b,c>0或a
注意:
如果,,那么
不等式两边同时乘上一个负数,要变号 .
不等式性质
探究5:同向可加性
如果,,那么
如果,,那么
如果,,那么
探究6:同向同正可乘性
如果, ,那么
探究7:同正可乘方性
如果,那么
不等式性质
(1)对称性:a>b .(2)传递性:a>b,b>c .(3)可加性:a>b .(4)可乘性:a>b,c>0 ;a>b,c<0 .(5)加法法则:a>b,c>d .(6)乘法法则:a>b>0,c>d>0 .(7)乘方法则:a>b>0 _____________________.
Topic. 03
03 不等式性质应用
[思路点拨] 本题可以利用不等式的性质直接判断命题的真假,也可以采用特殊值法判断.
D
不等式性质的应用
.
不等式性质的应用
不等式性质的应用
不等式性质的应用
证明:
不等式性质应用
3.若a>b,c>d,则下列不等关系中不一定成立的是( )A.a-b>d-c B.a+d>b+cC.a-c>b-c D.a-c<a-d
B
不等式性质的应用
4.与a>b等价的不等式是( )A.|a|>|b| B.a2>b2C.>1 D.a3>b3
D
不等式性质的应用
5.已知实数满足,,求,的取值范围;
解:
注意:
同向不等式具有可加性与可乘性(同正),但是不具有可减性与可除性,应用时要充分利用所给条件进行适当变形来求取值范围,注意变形的等价性。
不等式性质的应用
6.已知实数满足,,求的取值范围。
解:设
则,解得
即
,
Topic. 04
04 课堂小结
课堂小结
(1)对称性:a>b .
(2)传递性:a>b,b>c .
(3)可加性:a>b .
(4)可乘性:a>b,c>0 ;a>b,c<0 .
(5)加法法则:a>b,c>d .
(6)乘法法则:a>b>0,c>d>0 .
(7)乘方法则:a>b>0 _____________________.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
