13.3等腰三角形同步习题精讲课件(预习导航+堂堂清+日日清)
文档属性
| 名称 | 13.3等腰三角形同步习题精讲课件(预习导航+堂堂清+日日清) |  | |
| 格式 | zip | ||
| 文件大小 | 304.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-28 10:20:57 | ||
图片预览






文档简介
课件22张PPT。13.3 等腰三角形第1课时 等腰三角形的性质13.3 等腰三角形等腰三角形的性质:等腰三角形的两个 相等(简写成“等边对等 ”);等腰三角形的顶角平分线、底边上的 、底边上的中线互相重合(简写成“ ”)底角角高三线合一等腰三角形的有关概念 1.(3分)一个等腰三角形两边的长分别为4和9,那么这个三角形的周长是( )
A.13 B.17 C.22 D.17或22
2.(3分)等腰三角形底边长为5 cm,一腰上的中线把其周长分为两部分的差为3 cm,则腰长为( )
A.2 cm B.8 cm C.2 cm或8 cm D.不确定CB等腰三角形的性质 3.(3分)等腰三角形的对称轴是( )
A.底边上的中线 B.顶角平分线
C.底边上的高 D.底边的垂直平分线
4.(3分)已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
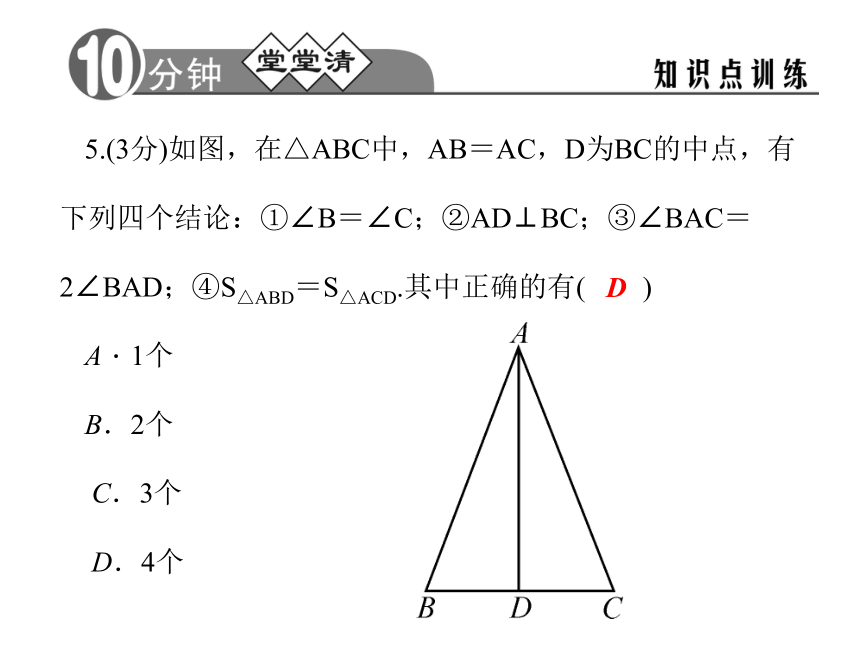
A.50° B.80° C.50°或80° D.40°或65°DC5.(3分)如图,在△ABC中,AB=AC,D为BC的中点,有下列四个结论:①∠B=∠C;②AD⊥BC;③∠BAC=2∠BAD;④S△ABD=S△ACD.其中正确的有( )
A.1个
B.2个
C.3个
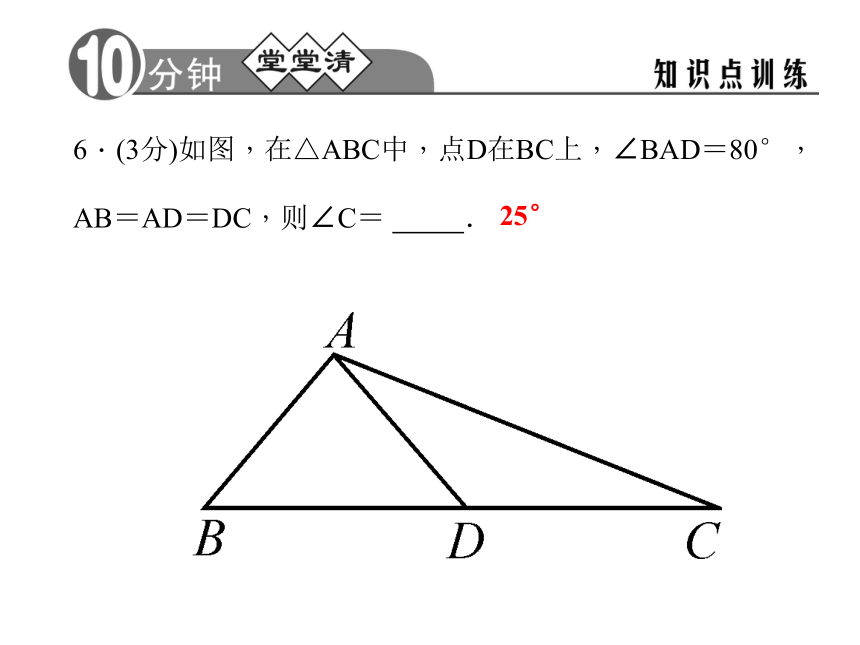
D.4个D6.(3分)如图,在△ABC中,点D在BC上,∠BAD=80°,AB=AD=DC,则∠C= .25°7.(6分)已知一个三角形两边长为4 cm,5 cm,且第三边长x为整数.
(1)由4 cm,5 cm,x cm为边可组成多少个不同的三角形?说说你的理由;
(2)如果这个三角形是等腰三角形,试确定x的值.
解:(1)x值可取2,3,4,5,6,7,8共有7个,因而可组成7个不同的三角形
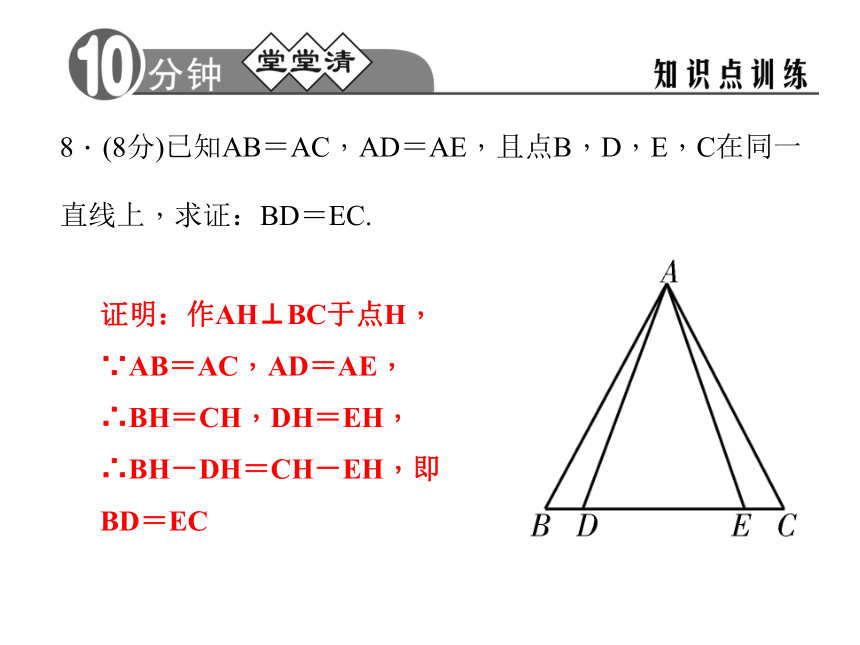
(2)x为4 cm或5 cm.8.(8分)已知AB=AC,AD=AE,且点B,D,E,C在同一直线上,求证:BD=EC.证明:作AH⊥BC于点H,∵AB=AC,AD=AE,∴BH=CH,DH=EH,∴BH-DH=CH-EH,即BD=EC9.(8分)如图,在△ABC中,点D在BC上,且有AB=AC=CD,BD=AD,求△ABC中各内角的度数.解:∵AB=AC=CD,∴∠B=∠C,∠1=∠2,∵BD=AD,∴∠B=∠3,又∵∠1=∠B+∠3,∠B+∠3+∠2+∠C=180°,∴∠B=36°,∠C=36°,∠BAC=108°【易错盘点】
【例】在平面直角坐标系中,已知A(2,-2),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P有________个.
【错解】__3__.
【错因分析】分类不完全.
【正解】__4__. 一、填空题(每小题5分,共15分)
10.已知一个等腰三角形的两内角的度数之比为1∶4,则这个等腰三角形顶角的度数为( )
A.20°
B.120°
C.20°或120°
D.36°C11.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )
A.100°
B.80°
C.70°
D.50°A12.如图,∠A=15°,AB=BC=CD=DE…,依次作下去,和AB相等的线段(不包括AB)最多可作( )
A.3条
B.4条
C.5条
D.6条C二、填空题(每小题5分,共15分)
13.如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD的三等分点,若△ABC的面积为12 cm2,则图中阴影部分的面积是 cm2.614.如图,已知AB=A1B,A1C=A1A2,A2D =A2A3,A3E=A3A4,若∠B=20°,则∠A4= .
15.等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角的度数是 .10°60°或120°三、解答题(共30分)
16.(8分)如图,△ABC中,AB=AC,点E在CA的延长线上,且∠AEF=∠AFE.试问直线EF和BC有何位置关系?为什么?(提示:过点A作AD⊥BC于点D)解:EF⊥BC.理由:过A点作AD⊥BC于点D.∵AB=AC,∴∠BAD=∠BAC.∵∠BAC=∠AEF+∠AFE,∠AEF=∠AFE,∴∠AFE=∠BAC=∠BAD,∴EF∥AD,又∵AD⊥BC,∴EF⊥BC17.(10分)如图,△ABC中,AD⊥BC于点D,若AB+BD=CD,求证:∠B=2∠C.(提示:在DC上截取DE=BD,连接AE)证明:在DC上截取BD=DE,连接AE.∵BD=DE,AD⊥BE,∴AD是BE的垂直平分线,∴AB=AE,∴∠B=∠AEB.又AB+BD=CD,而BD=DE,∴AB=EC,又AB=AE,∴AE=EC,∴∠C=∠EAC,∴∠AEB=∠EAC+∠C=2∠C,∴∠B=2∠C. 【综合运用】
18.(12分)(1)如图①,在△ABC中,AB=AC,P为底边BC上一点,PD⊥AB于点D,PE⊥AC于点E,CF⊥AB于点F,求证:PD+PE=CF;
(2)如图②所示,若点P在BC的延长线上,请你猜想PD,PE,CF之间存在的等量关系,写出你的猜想并加以证明.证明:(1)连接AP,则S△ABP+S△ACP=S△ABC,∵S△ABC= AB·CF,S△ABP= AB·PD,S△ACP= AC·PE,又∵AB=AC,∴ AB·CF= AB·PD+ AB·PE.即 AB·CF=AB(PD+PE),CF=PD+PE
(2)猜想CF=PD-PE.证明如下,连接AP,则S△ABC=S△ABP-S△ACP,∴ AB·CF= AB·PD- AB·PE,∴CF=PD-PE
A.13 B.17 C.22 D.17或22
2.(3分)等腰三角形底边长为5 cm,一腰上的中线把其周长分为两部分的差为3 cm,则腰长为( )
A.2 cm B.8 cm C.2 cm或8 cm D.不确定CB等腰三角形的性质 3.(3分)等腰三角形的对称轴是( )
A.底边上的中线 B.顶角平分线
C.底边上的高 D.底边的垂直平分线
4.(3分)已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°DC5.(3分)如图,在△ABC中,AB=AC,D为BC的中点,有下列四个结论:①∠B=∠C;②AD⊥BC;③∠BAC=2∠BAD;④S△ABD=S△ACD.其中正确的有( )
A.1个
B.2个
C.3个
D.4个D6.(3分)如图,在△ABC中,点D在BC上,∠BAD=80°,AB=AD=DC,则∠C= .25°7.(6分)已知一个三角形两边长为4 cm,5 cm,且第三边长x为整数.
(1)由4 cm,5 cm,x cm为边可组成多少个不同的三角形?说说你的理由;
(2)如果这个三角形是等腰三角形,试确定x的值.
解:(1)x值可取2,3,4,5,6,7,8共有7个,因而可组成7个不同的三角形
(2)x为4 cm或5 cm.8.(8分)已知AB=AC,AD=AE,且点B,D,E,C在同一直线上,求证:BD=EC.证明:作AH⊥BC于点H,∵AB=AC,AD=AE,∴BH=CH,DH=EH,∴BH-DH=CH-EH,即BD=EC9.(8分)如图,在△ABC中,点D在BC上,且有AB=AC=CD,BD=AD,求△ABC中各内角的度数.解:∵AB=AC=CD,∴∠B=∠C,∠1=∠2,∵BD=AD,∴∠B=∠3,又∵∠1=∠B+∠3,∠B+∠3+∠2+∠C=180°,∴∠B=36°,∠C=36°,∠BAC=108°【易错盘点】
【例】在平面直角坐标系中,已知A(2,-2),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P有________个.
【错解】__3__.
【错因分析】分类不完全.
【正解】__4__. 一、填空题(每小题5分,共15分)
10.已知一个等腰三角形的两内角的度数之比为1∶4,则这个等腰三角形顶角的度数为( )
A.20°
B.120°
C.20°或120°
D.36°C11.如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )
A.100°
B.80°
C.70°
D.50°A12.如图,∠A=15°,AB=BC=CD=DE…,依次作下去,和AB相等的线段(不包括AB)最多可作( )
A.3条
B.4条
C.5条
D.6条C二、填空题(每小题5分,共15分)
13.如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD的三等分点,若△ABC的面积为12 cm2,则图中阴影部分的面积是 cm2.614.如图,已知AB=A1B,A1C=A1A2,A2D =A2A3,A3E=A3A4,若∠B=20°,则∠A4= .
15.等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角的度数是 .10°60°或120°三、解答题(共30分)
16.(8分)如图,△ABC中,AB=AC,点E在CA的延长线上,且∠AEF=∠AFE.试问直线EF和BC有何位置关系?为什么?(提示:过点A作AD⊥BC于点D)解:EF⊥BC.理由:过A点作AD⊥BC于点D.∵AB=AC,∴∠BAD=∠BAC.∵∠BAC=∠AEF+∠AFE,∠AEF=∠AFE,∴∠AFE=∠BAC=∠BAD,∴EF∥AD,又∵AD⊥BC,∴EF⊥BC17.(10分)如图,△ABC中,AD⊥BC于点D,若AB+BD=CD,求证:∠B=2∠C.(提示:在DC上截取DE=BD,连接AE)证明:在DC上截取BD=DE,连接AE.∵BD=DE,AD⊥BE,∴AD是BE的垂直平分线,∴AB=AE,∴∠B=∠AEB.又AB+BD=CD,而BD=DE,∴AB=EC,又AB=AE,∴AE=EC,∴∠C=∠EAC,∴∠AEB=∠EAC+∠C=2∠C,∴∠B=2∠C. 【综合运用】
18.(12分)(1)如图①,在△ABC中,AB=AC,P为底边BC上一点,PD⊥AB于点D,PE⊥AC于点E,CF⊥AB于点F,求证:PD+PE=CF;
(2)如图②所示,若点P在BC的延长线上,请你猜想PD,PE,CF之间存在的等量关系,写出你的猜想并加以证明.证明:(1)连接AP,则S△ABP+S△ACP=S△ABC,∵S△ABC= AB·CF,S△ABP= AB·PD,S△ACP= AC·PE,又∵AB=AC,∴ AB·CF= AB·PD+ AB·PE.即 AB·CF=AB(PD+PE),CF=PD+PE
(2)猜想CF=PD-PE.证明如下,连接AP,则S△ABC=S△ABP-S△ACP,∴ AB·CF= AB·PD- AB·PE,∴CF=PD-PE
