13.2画轴对称图形例题与讲解
文档属性
| 名称 | 13.2画轴对称图形例题与讲解 | 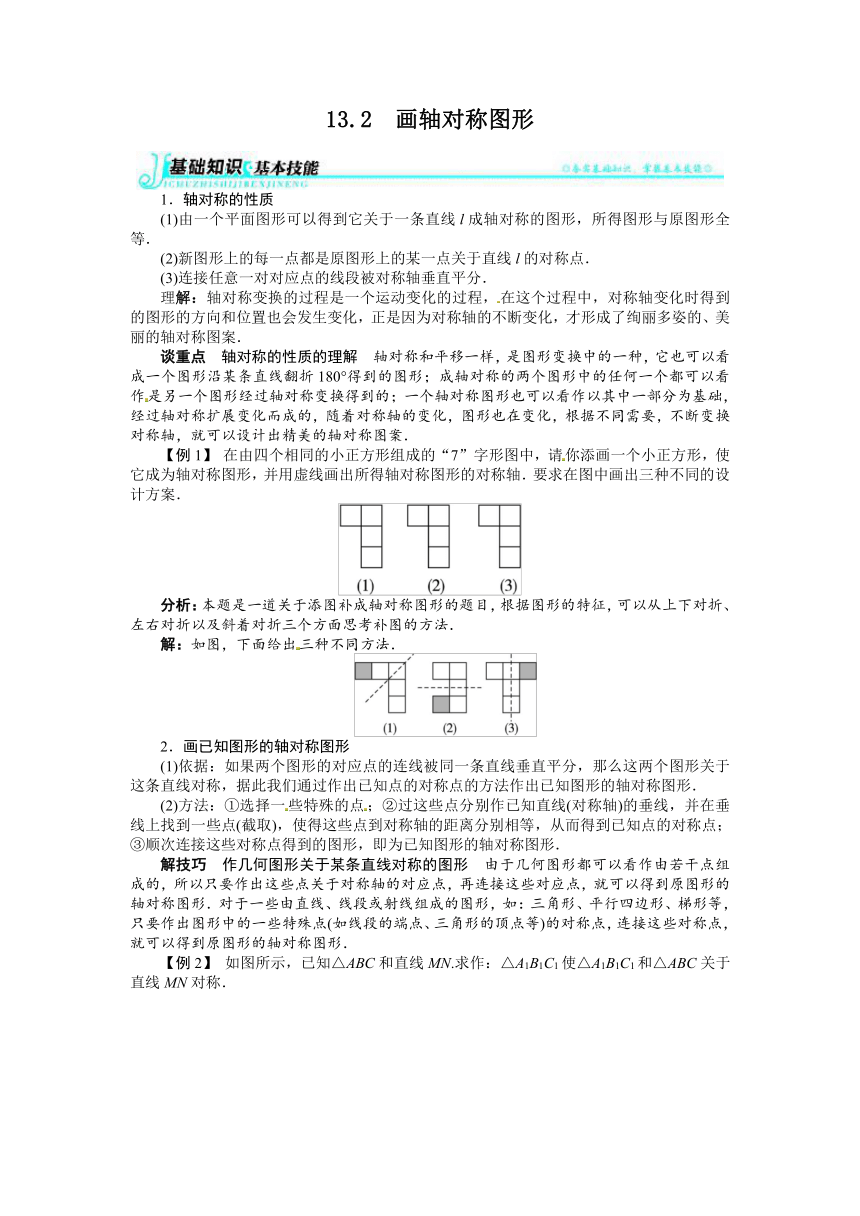 | |
| 格式 | zip | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-28 08:16:30 | ||
图片预览

文档简介
13.2 画轴对称图形
1.轴对称的性质
(1)由一个平面图形可以得到它关于一条直线l成轴对称的图形,所得图形与原图形全等.
(2)新图形上的每一点都是原图形上的某一点关于直线l的对称点.
(3)连接任意一对对应点的线段被对称轴垂直平分.
理解:轴对称变换的过程是一个运动变化的过程,在这个过程中,对称轴变化时得到的图形的方向和位置也会发生变化,正是因为对称轴的不断变化,才形成了绚丽多姿的、美丽的轴对称图案.
谈重点 轴对称的性质的理解 轴对称和平移一样,是图形变换中的一种,它也可以看成一个图形沿某条直线翻折180°得到的图形;成轴对称的两个图形中的任何一个都可以看作是另一个图形经过轴对称变换得到的;一个轴对称图形也可以看作以其中一部分为基础,经过轴对称扩展变化而成的,随着对称轴的变化,图形也在变化,根据不同需要,不断变换对称轴,就可以设计出精美的轴对称图案.
【例1】 在由四个相同的小正方形组成的“7”字形图中,请你添画一个小正方形,使它成为轴对称图形,并用虚线画出所得轴对称图形的对称轴.要求在图中画出三种不同的设计方案.
分析:本题是一道关于添图补成轴对称图形的题目,根据图形的特征,可以从上下对折、左右对折以及斜着对折三个方面思考补图的方法.
解:如图,下面给出三种不同方法.
2.画已知图形的轴对称图形
(1)依据:如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称,据此我们通过作出已知点的对称点的方法作出已知图形的轴对称图形.
(2)方法:①选择一些特殊的点;②过这些点分别作已知直线(对称轴)的垂线,并在垂线上找到一些点(截取),使得这些点到对称轴的距离分别相等,从而得到已知点的对称点;③顺次连接这些对称点得到的图形,即为已知图形的轴对称图形.
解技巧 作几何图形关于某条直线对称的图形 由于几何图形都可以看作由若干点组成的,所以只要作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形.对于一些由直线、线段或射线组成的图形,如:三角形、平行四边形、梯形等,只要作出图形中的一些特殊点(如线段的端点、三角形的顶点等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
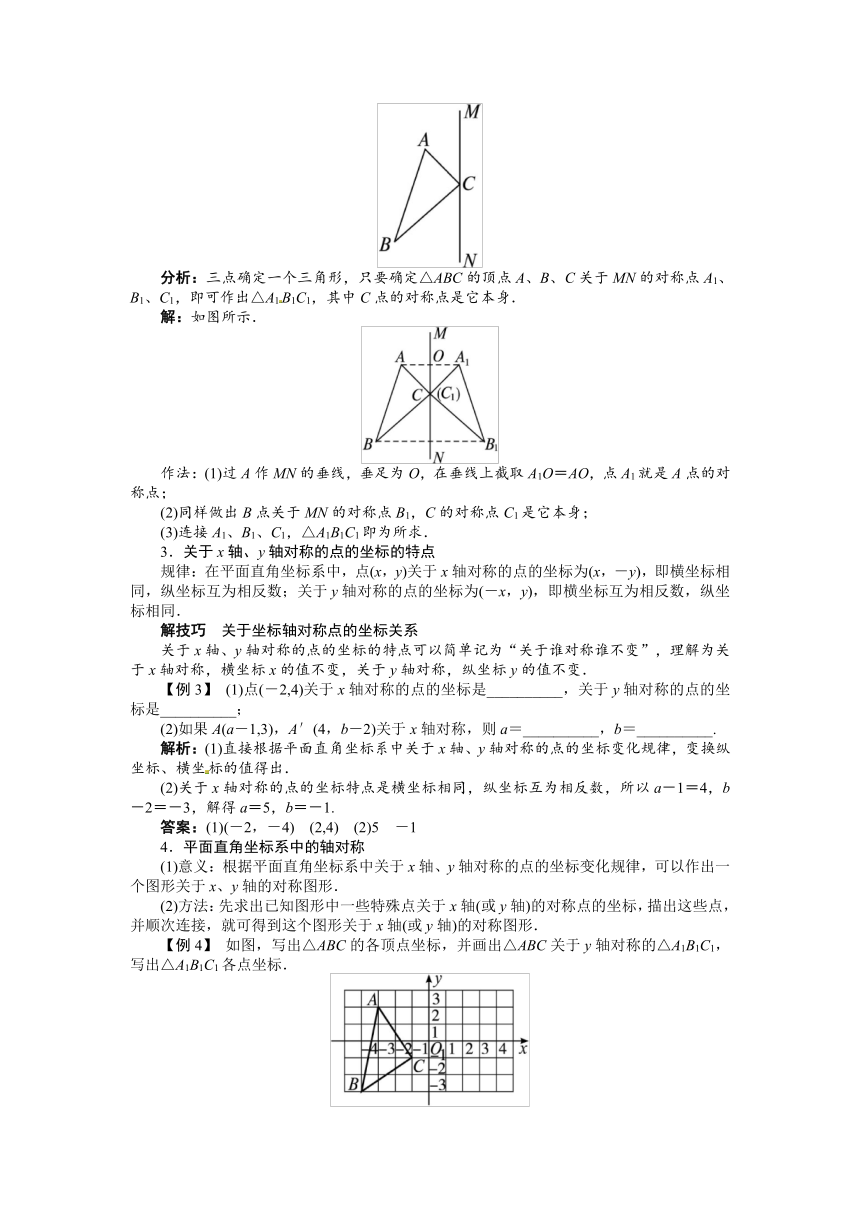
【例2】 如图所示,已知△ABC和直线MN.求作:△A1B1C1使△A1B1C1和△ABC关于直线MN对称.
分析:三点确定一个三角形,只要确定△ABC的顶点A、B、C关于MN的对称点A1、B1、C1,即可作出△A1B1C1,其中C点的对称点是它本身.
解:如图所示.
作法:(1)过A作MN的垂线,垂足为O,在垂线上截取A1O=AO,点A1就是A点的对称点;
(2)同样做出B点关于MN的对称点B1,C的对称点C1是它本身;
(3)连接A1、B1、C1,△A1B1C1即为所求.
3.关于x轴、y轴对称的点的坐标的特点
规律:在平面直角坐标系中,点(x,y)关于x轴对称的点的坐标为(x,-y),即横坐标相同,纵坐标互为相反数;关于y轴对称的点的坐标为(-x,y),即横坐标互为相反数,纵坐标相同.
解技巧 关于坐标轴对称点的坐标关系
关于x轴、y轴对称的点的坐标的特点可以简单记为“关于谁对称谁不变”,理解为关于x轴对称,横坐标x的值不变,关于y轴对称,纵坐标y的值不变.
【例3】 (1)点(-2,4)关于x轴对称的点的坐标是__________,关于y轴对称的点的坐标是__________;
(2)如果A(a-1,3),A′(4,b-2)关于x轴对称,则a=__________,b=__________.
解析:(1)直接根据平面直角坐标系中关于x轴、y轴对称的点的坐标变化规律,变换纵坐标、横坐标的值得出.
(2)关于x轴对称的点的坐标特点是横坐标相同,纵坐标互为相反数,所以a-1=4,b-2=-3,解得a=5,b=-1.
答案:(1)(-2,-4) (2,4) (2)5 -1
4.平面直角坐标系中的轴对称
(1)意义:根据平面直角坐标系中关于x轴、y轴对称的点的坐标变化规律,可以作出一个图形关于x、y轴的对称图形.
(2)方法:先求出已知图形中一些特殊点关于x轴(或y轴)的对称点的坐标,描出这些点,并顺次连接,就可得到这个图形关于x轴(或y轴)的对称图形.
【例4】 如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,写出△A1B1C1各点坐标.
分析:写出△ABC各顶点的坐标,再根据关于y轴对称的点的坐标变化规律,分别求出点A、B、C关于y轴的对称点A1,B1,C1的坐标,描出这些点,并顺次连接,即可得到△A1B1C1.
解:(1)由图可知,△ABC各顶点的坐标为A(-3,2),B(-4,-3),C(-1,-1);
(2)A、B、C关于y轴的对称点A1,B1,C1的坐标分别是(3,2),(4,-3),(1,-1).在坐标系中描出点A1,B1,C1,并顺次连接,如图所示,△A1B1C1即为所求.
5.轴对称图形的画法应用
已知一个图形和一条直线,可以作出这个图形关于这条直线的对称图形,关键在于选择特殊的点,作出这些点的对称点,顺次连接即可得到已知图形的轴对称图形,由于几何图形是由点组成的,选择的点越多,图形越准确.随着计算机技术的推广,用几何画板、画图板、粘贴等手段能画出更准确的轴对称图形.
6.平面直角坐标系中轴对称的应用
平面直角坐标系中的轴对称应用主要有三种情况:
①由给定的点的坐标求这点关于x轴或y轴的点的坐标;
②已知两点关于x轴或y轴对称,求坐标或坐标中未知数的值;
③已知坐标系中的一个图形,画出此图形关于x轴或y轴对称的图形.
析规律 作一个图形关于x轴、y轴对称的图形 关于x轴、y轴对称的点的坐标变化规律是解决这三类问题的基础和关键,根据“关于x轴对称的点的横坐标相同,纵坐标互为相反数;关于y轴对称的点的横坐标互为相反数,纵坐标相同”求出坐标、描点、画出图形或列出相关式子解决问题.
【例5】 如图1是由一个圆、一个半圆和一个三角形组成的图形,请你以直线AB为对称轴,把原图补成轴对称图形.
分析:半圆的对称图形还是半圆,三角形的对称点有两点在对称轴上,只要找到P点关于AB的对称点Q即可.
解:(1)以O为圆心,以OC的长为半径画半圆;
(2)过P作AB的垂线,垂足为D,在垂线上截取QD=PD,连接CQ,如图2所示即为所求.
【例6-1】 已知M(a-2,b+1)与N(b-3,a+2)关于x轴对称,求a+b的值.
分析:由关于x轴对称的点的坐标规律,先列方程组求出a,b的值,再计算a+b的值.
解:由题意,得解得
所以a+b=-3.
点拨:也可由b+1=-(a+2)直接得a+b=-3.
【例6-2】 已知点P(2m-3,3-m)关于y轴对称的点在第二象限,试确定整数m的值.
分析:本例并非直接利用坐标的变化规律来解题,而是考查对称点的位置,根据点所在的象限列不等式组去求解.
解:由于点P关于y轴的对称点在第二象限,
则点P在第一象限,所以
解得<m<3,因为m为整数,所以m=2.
7.轴对称图形设计
日常生活中有很多图形是轴对称图形,这些图形给我们以美的视觉享受,使我们的生活变得更加绚丽多彩,实际上这许许多多精美的图案很多是由一些简单的图形通过轴对称变化得到的,一个简单的图形,通过不断的轴对称变换,就会变得丰富多彩,绚丽多姿,就像我们的民间剪纸艺术,也是通过折叠、剪裁、展开得到美丽图案的.对称轴不同,变化的方向和位置就不同,从而变化出各种图案.随着计算机技术的推广,我们可以通过复制、粘贴、翻折等方法制作出更复杂、美丽的轴对称图形,甚至让它们动起来.
8.轴对称中的剪纸问题
剪纸艺术是我国最美丽的民间艺术之一,而剪纸中的轴对称问题也是近几年中考的热点,它重点考查同学们动手操作能力、空间想象能力,同时也考查对轴对称图形有关性质的认识.此类题目大多是将长方形或正方形纸片通过折叠、剪裁,观察展开后得到的图形.此类题目往往经过多次轴对称变换,展开后变化较大,因而要注意观察,抓住主要特点识别.
9.点P(x,y)关于直线x=m,直线y=n对称的点的坐标
轴对称是关于某条直线的对称,在平面直角坐标系中,除了关于x轴、y轴对称外,图形还能关于平行于x轴、y轴的任意一条直线轴对称,并且坐标变化规律也不尽相同.但不论关于任何一条直线轴对称,它们都是轴对称,都具备轴对称性质,我们仍然能根据轴对称性质,发现其中规律,画出轴对称图形,得出对应点的坐标.
析规律 关于直线x=m的对称点的坐标关系 点(x,y)关于直线x=m对称的点的坐标关系是:两对称点横坐标之和等于2m,即所求点的横坐标x1=2m-x,纵坐标不变;关于直线y=n对称的点的坐标关系是:横坐标不变,两对称点纵坐标之和等于2n,即所求点的纵坐标y1=2n-y.
【例7】 (方案设计题)如图,在网格中有两个全等的图形(阴影部分),你能用这两个图形拼成轴对称图形吗,试分别在给出的图(1)、图(2)中画出两种不同的拼法.
分析:由于对称轴不同、图形位置不同,得到的轴对称图形也不同,我们可以用不同的网格线作为对称轴,来构造不同的轴对称图案.这是一道开放题,答案不唯一,同学们可以开动脑筋发挥你的想象力,绘制出不同的图案.
解:下面提供部分答案,仅供参考,不同的画法例举如下(如图所示):
【例8】 (操作题)如图,将正方形纸片按图中(1)、(2)的方式依次对折后,再沿(3)中的虚线裁剪,最后将(4)中的纸片打开铺平,所得图案应该是下面图案中的( ).
解析:方法一:观察图形,是将正方形纸片折叠两次,因此是两次轴对称,并且裁剪部位在折叠的最中间,展开后中间应是个小正方形,另一剪裁部位在最上边沿,展开后应是原正方形上下边沿的独立缺口,所以只有B选项适合.方法二:将所给四个选项分别先竖后横依次折叠,再结合最后的剪裁综合分析,A的剪裁既有上下,也有左右,也不适合,C、D的剪裁部位不在最中间也不合适,只有选项B经过两次折叠,符合图(4)裁剪情况,故选B.
答案:B
【例9】 如图1,作△ABC关于直线m和直线n对称的图形,并写出各对称顶点的坐标.
图1 图2
解:(1)如图2中,△A′B′C′和△A″B″C″即为所求图形.
(2)关于直线m对称的△A′B′C′各顶点的坐标分别为A′(4,4)、B′(5,0)、C′(2,1),关于直线n对称的△A″B″C″各顶点的坐标为A″(-2,-6)、B″(-3,-2)、C″(0,-3).
1.轴对称的性质
(1)由一个平面图形可以得到它关于一条直线l成轴对称的图形,所得图形与原图形全等.
(2)新图形上的每一点都是原图形上的某一点关于直线l的对称点.
(3)连接任意一对对应点的线段被对称轴垂直平分.
理解:轴对称变换的过程是一个运动变化的过程,在这个过程中,对称轴变化时得到的图形的方向和位置也会发生变化,正是因为对称轴的不断变化,才形成了绚丽多姿的、美丽的轴对称图案.
谈重点 轴对称的性质的理解 轴对称和平移一样,是图形变换中的一种,它也可以看成一个图形沿某条直线翻折180°得到的图形;成轴对称的两个图形中的任何一个都可以看作是另一个图形经过轴对称变换得到的;一个轴对称图形也可以看作以其中一部分为基础,经过轴对称扩展变化而成的,随着对称轴的变化,图形也在变化,根据不同需要,不断变换对称轴,就可以设计出精美的轴对称图案.
【例1】 在由四个相同的小正方形组成的“7”字形图中,请你添画一个小正方形,使它成为轴对称图形,并用虚线画出所得轴对称图形的对称轴.要求在图中画出三种不同的设计方案.
分析:本题是一道关于添图补成轴对称图形的题目,根据图形的特征,可以从上下对折、左右对折以及斜着对折三个方面思考补图的方法.
解:如图,下面给出三种不同方法.
2.画已知图形的轴对称图形
(1)依据:如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称,据此我们通过作出已知点的对称点的方法作出已知图形的轴对称图形.
(2)方法:①选择一些特殊的点;②过这些点分别作已知直线(对称轴)的垂线,并在垂线上找到一些点(截取),使得这些点到对称轴的距离分别相等,从而得到已知点的对称点;③顺次连接这些对称点得到的图形,即为已知图形的轴对称图形.
解技巧 作几何图形关于某条直线对称的图形 由于几何图形都可以看作由若干点组成的,所以只要作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形.对于一些由直线、线段或射线组成的图形,如:三角形、平行四边形、梯形等,只要作出图形中的一些特殊点(如线段的端点、三角形的顶点等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
【例2】 如图所示,已知△ABC和直线MN.求作:△A1B1C1使△A1B1C1和△ABC关于直线MN对称.
分析:三点确定一个三角形,只要确定△ABC的顶点A、B、C关于MN的对称点A1、B1、C1,即可作出△A1B1C1,其中C点的对称点是它本身.
解:如图所示.
作法:(1)过A作MN的垂线,垂足为O,在垂线上截取A1O=AO,点A1就是A点的对称点;
(2)同样做出B点关于MN的对称点B1,C的对称点C1是它本身;
(3)连接A1、B1、C1,△A1B1C1即为所求.
3.关于x轴、y轴对称的点的坐标的特点
规律:在平面直角坐标系中,点(x,y)关于x轴对称的点的坐标为(x,-y),即横坐标相同,纵坐标互为相反数;关于y轴对称的点的坐标为(-x,y),即横坐标互为相反数,纵坐标相同.
解技巧 关于坐标轴对称点的坐标关系
关于x轴、y轴对称的点的坐标的特点可以简单记为“关于谁对称谁不变”,理解为关于x轴对称,横坐标x的值不变,关于y轴对称,纵坐标y的值不变.
【例3】 (1)点(-2,4)关于x轴对称的点的坐标是__________,关于y轴对称的点的坐标是__________;
(2)如果A(a-1,3),A′(4,b-2)关于x轴对称,则a=__________,b=__________.
解析:(1)直接根据平面直角坐标系中关于x轴、y轴对称的点的坐标变化规律,变换纵坐标、横坐标的值得出.
(2)关于x轴对称的点的坐标特点是横坐标相同,纵坐标互为相反数,所以a-1=4,b-2=-3,解得a=5,b=-1.
答案:(1)(-2,-4) (2,4) (2)5 -1
4.平面直角坐标系中的轴对称
(1)意义:根据平面直角坐标系中关于x轴、y轴对称的点的坐标变化规律,可以作出一个图形关于x、y轴的对称图形.
(2)方法:先求出已知图形中一些特殊点关于x轴(或y轴)的对称点的坐标,描出这些点,并顺次连接,就可得到这个图形关于x轴(或y轴)的对称图形.
【例4】 如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,写出△A1B1C1各点坐标.
分析:写出△ABC各顶点的坐标,再根据关于y轴对称的点的坐标变化规律,分别求出点A、B、C关于y轴的对称点A1,B1,C1的坐标,描出这些点,并顺次连接,即可得到△A1B1C1.
解:(1)由图可知,△ABC各顶点的坐标为A(-3,2),B(-4,-3),C(-1,-1);
(2)A、B、C关于y轴的对称点A1,B1,C1的坐标分别是(3,2),(4,-3),(1,-1).在坐标系中描出点A1,B1,C1,并顺次连接,如图所示,△A1B1C1即为所求.
5.轴对称图形的画法应用
已知一个图形和一条直线,可以作出这个图形关于这条直线的对称图形,关键在于选择特殊的点,作出这些点的对称点,顺次连接即可得到已知图形的轴对称图形,由于几何图形是由点组成的,选择的点越多,图形越准确.随着计算机技术的推广,用几何画板、画图板、粘贴等手段能画出更准确的轴对称图形.
6.平面直角坐标系中轴对称的应用
平面直角坐标系中的轴对称应用主要有三种情况:
①由给定的点的坐标求这点关于x轴或y轴的点的坐标;
②已知两点关于x轴或y轴对称,求坐标或坐标中未知数的值;
③已知坐标系中的一个图形,画出此图形关于x轴或y轴对称的图形.
析规律 作一个图形关于x轴、y轴对称的图形 关于x轴、y轴对称的点的坐标变化规律是解决这三类问题的基础和关键,根据“关于x轴对称的点的横坐标相同,纵坐标互为相反数;关于y轴对称的点的横坐标互为相反数,纵坐标相同”求出坐标、描点、画出图形或列出相关式子解决问题.
【例5】 如图1是由一个圆、一个半圆和一个三角形组成的图形,请你以直线AB为对称轴,把原图补成轴对称图形.
分析:半圆的对称图形还是半圆,三角形的对称点有两点在对称轴上,只要找到P点关于AB的对称点Q即可.
解:(1)以O为圆心,以OC的长为半径画半圆;
(2)过P作AB的垂线,垂足为D,在垂线上截取QD=PD,连接CQ,如图2所示即为所求.
【例6-1】 已知M(a-2,b+1)与N(b-3,a+2)关于x轴对称,求a+b的值.
分析:由关于x轴对称的点的坐标规律,先列方程组求出a,b的值,再计算a+b的值.
解:由题意,得解得
所以a+b=-3.
点拨:也可由b+1=-(a+2)直接得a+b=-3.
【例6-2】 已知点P(2m-3,3-m)关于y轴对称的点在第二象限,试确定整数m的值.
分析:本例并非直接利用坐标的变化规律来解题,而是考查对称点的位置,根据点所在的象限列不等式组去求解.
解:由于点P关于y轴的对称点在第二象限,
则点P在第一象限,所以
解得<m<3,因为m为整数,所以m=2.
7.轴对称图形设计
日常生活中有很多图形是轴对称图形,这些图形给我们以美的视觉享受,使我们的生活变得更加绚丽多彩,实际上这许许多多精美的图案很多是由一些简单的图形通过轴对称变化得到的,一个简单的图形,通过不断的轴对称变换,就会变得丰富多彩,绚丽多姿,就像我们的民间剪纸艺术,也是通过折叠、剪裁、展开得到美丽图案的.对称轴不同,变化的方向和位置就不同,从而变化出各种图案.随着计算机技术的推广,我们可以通过复制、粘贴、翻折等方法制作出更复杂、美丽的轴对称图形,甚至让它们动起来.
8.轴对称中的剪纸问题
剪纸艺术是我国最美丽的民间艺术之一,而剪纸中的轴对称问题也是近几年中考的热点,它重点考查同学们动手操作能力、空间想象能力,同时也考查对轴对称图形有关性质的认识.此类题目大多是将长方形或正方形纸片通过折叠、剪裁,观察展开后得到的图形.此类题目往往经过多次轴对称变换,展开后变化较大,因而要注意观察,抓住主要特点识别.
9.点P(x,y)关于直线x=m,直线y=n对称的点的坐标
轴对称是关于某条直线的对称,在平面直角坐标系中,除了关于x轴、y轴对称外,图形还能关于平行于x轴、y轴的任意一条直线轴对称,并且坐标变化规律也不尽相同.但不论关于任何一条直线轴对称,它们都是轴对称,都具备轴对称性质,我们仍然能根据轴对称性质,发现其中规律,画出轴对称图形,得出对应点的坐标.
析规律 关于直线x=m的对称点的坐标关系 点(x,y)关于直线x=m对称的点的坐标关系是:两对称点横坐标之和等于2m,即所求点的横坐标x1=2m-x,纵坐标不变;关于直线y=n对称的点的坐标关系是:横坐标不变,两对称点纵坐标之和等于2n,即所求点的纵坐标y1=2n-y.
【例7】 (方案设计题)如图,在网格中有两个全等的图形(阴影部分),你能用这两个图形拼成轴对称图形吗,试分别在给出的图(1)、图(2)中画出两种不同的拼法.
分析:由于对称轴不同、图形位置不同,得到的轴对称图形也不同,我们可以用不同的网格线作为对称轴,来构造不同的轴对称图案.这是一道开放题,答案不唯一,同学们可以开动脑筋发挥你的想象力,绘制出不同的图案.
解:下面提供部分答案,仅供参考,不同的画法例举如下(如图所示):
【例8】 (操作题)如图,将正方形纸片按图中(1)、(2)的方式依次对折后,再沿(3)中的虚线裁剪,最后将(4)中的纸片打开铺平,所得图案应该是下面图案中的( ).
解析:方法一:观察图形,是将正方形纸片折叠两次,因此是两次轴对称,并且裁剪部位在折叠的最中间,展开后中间应是个小正方形,另一剪裁部位在最上边沿,展开后应是原正方形上下边沿的独立缺口,所以只有B选项适合.方法二:将所给四个选项分别先竖后横依次折叠,再结合最后的剪裁综合分析,A的剪裁既有上下,也有左右,也不适合,C、D的剪裁部位不在最中间也不合适,只有选项B经过两次折叠,符合图(4)裁剪情况,故选B.
答案:B
【例9】 如图1,作△ABC关于直线m和直线n对称的图形,并写出各对称顶点的坐标.
图1 图2
解:(1)如图2中,△A′B′C′和△A″B″C″即为所求图形.
(2)关于直线m对称的△A′B′C′各顶点的坐标分别为A′(4,4)、B′(5,0)、C′(2,1),关于直线n对称的△A″B″C″各顶点的坐标为A″(-2,-6)、B″(-3,-2)、C″(0,-3).
