21.3 实际问题与一元二次方程(1)——传染问题 课件(共29张PPT)
文档属性
| 名称 | 21.3 实际问题与一元二次方程(1)——传染问题 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 23:07:31 | ||
图片预览








文档简介
(共29张PPT)
21.3实际问题与一元二次方程(1)
传染问题
人教版九年级上册
知识回顾
1.解一元二次方程有哪些方法?
直接开平方法、配方法、公式法、因式分解法.
2.列一元二次方程解应用题的步骤?
①审题,
②设出未知数,
③找等量关系,
④列方程,
⑤解方程,
⑥验根,
⑦答.
教学目标
1.通过解决“传染问题”,体验建立方程模型解决问题的一般过程;
2.通过分析、总结,找到传染问题数量关系的通性;
3.在解决问题的过程中体会一元二次方程的数学模型作用,增强应用意识和应用能力。
新知导入
若一人患流感,每轮能传染5个人,则第一轮过后共有 个人患了流感,第二轮过后共有 个人患了流感.
6
36
分析:
新知探究
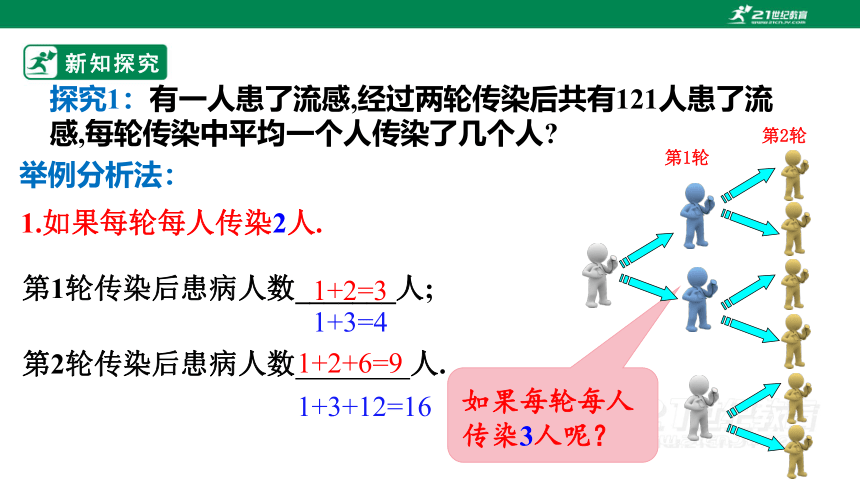
探究1:有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
第1轮传染后患病人数_______人;
举例分析法:
1.如果每轮每人传染2人.
第2轮传染后患病人数 人.
第2轮
第1轮
如果每轮每人传染3人呢?
1+2=3
1+2+6=9
1+3=4
1+3+12=16
新知探究
分析 :设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
第2轮
小明
1
2
x
第1轮
小明
注意:不要忽视小明的二次传染
第1轮传染后患病人数_______人;
第2轮传染后患病人数______________人.
列表可得
[1+x+(1+x)x]
(1+x)
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
新知探究
x1= , x2= .
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去)
10
解:设每轮传染中平均一个人传染了x个人.
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,所以一定要进行检验.
例1 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
设
列
解
检
答
新知探究
传染源 新增患者人数 本轮结束患者总人数
第一轮 1 1 x=x 1+x
第二轮 1+x (1+x)x 1+x+(1+x)x=
第三轮
第n轮
思考:如果按这样的传染速度, n轮后传染后有多少人患了流感
(1+x)n
经过n轮传染后共有(1+x)n人患流感.
(1+x)2
(1+x)2 x
(1+x)2+(1+x)2 x =
(1+x)3
(1+x)2
如果按照这样的传染速度,三轮传染后有多少人患流感
若最终有b人患流感,则(1+x)n=b人患流感.
(1+x)2+(1+x)2 x =121+121×10=1331人 或 (10+1)3=1331
新知小结
传染类型关键问题
1.患者 (传染源)只参与一轮的传染还是每轮都一直在传染
2.每一轮有多少人 (传染源)在传染
3.每轮新增多少患者
4.累计患者总数是多少
新知小结
传染问题的数量关系
(传染源每轮都一直在传染)
a(x+1)n=b
原有量(a)-------传播前的数量
传播速度(x)-------一个传播多少个
轮数(n)-------传播多少轮
最终量(b)-------经过传播后的数量
新知练习
1.某种电脑病毒传播非常快,如果有一台电脑被感染,经过两轮感染后就会有81台电脑被感染。请解释:每轮感染中平均一台电脑会感染几台电脑 若病毒得不到有效控制,三轮感染后,被感染的电脑会不会超过700台
解:设平均一台电脑会感染 x 台电脑,依题意得
(x+1)2=81
x1= , x2= .
解得
-10
(不合题意,舍去)
8
第三轮感染中被感染的电脑台数为:
答:每轮感染中平均一台电脑会感染8台电脑,若病毒得不到有效控制,三轮感染后,被感染的电脑会超过700台。
(1+8)3=729>700
a(x+1)n=b
原有量(a)-------1
传播速度(x)-------x
轮数(n)-------2
最终量(b)-------81
新知探究
例2 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
主干
解:设主干长出x个支干,则每个支干长也出 x个小分支。
新知探究
例2 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支
解:设主干长出x个支干,则每个支干长也出 x个小分支。
1+x+x2=91
整理得,
x2+x-90=0
x1=9,x2=-10(不合题意,舍去)
解得,
答:每个支干长出9个小分支。
设
列
解
检
答
审
新知探究
1.分析例1和例2中的数量关系,它们有何联系和区别
交流讨论
例2 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支
例1 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
联系:表格梳理
(1+x)2=121
1+x+x2=91
区别:
每名患者每轮都传染
即传染源参加每一轮的传染
每个支干只长一次
即传染源只参加一轮的传染
新知探究
交流讨论
例1和例2的联系和区别:
传染源参加每一轮的传染
传染源只参加一轮的传染
新知探究
交流讨论
2.解决传染问题有什么分析技巧?
(1)可利用图形或表格梳理数量关系
(2) 关注起始值、新增数量、轮数和最终量,找出变化规律.
新知探究
你若和班级所有同学都握手,你需握手多少次?
例3 在某次聚会上,每两人都握了一次手,所有人共握手10次,求有多少人参加这次聚会.
新知探究
设有x个人参加这次聚会,
思考:
1.则每个人与 人握手;
2.全班共握手 次(用含有x的式子表示);
3.依题意,可列方程为:_______________________.
( x - 1 )
新知探究
例3 在某次聚会上,每两人都握了一次手,所有人共握手10次,求有多少人参加这次聚会.
解:设有x个人参加这次聚会,
x1= , x2= .
解得
-4
(不合题意,舍去)
5
答:有5人参加这次聚会.
新知练习
2.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有飞机场( )
A.4个 B.5个 C.6个 D.7个
思考:
设这个航空公司共有飞机场x个,
1.则每个机场开辟 条航线;
2.所有机场共开辟 条航线(用含有x的式子表示);
3.依题意,可列方程为:_____________.
( x - 1 )
B
新知典例
例4 两个数的和是14,积是33,求这两个数.
答:这两个数分别为3,11.
解:设其中一个数为x,则另一个数为14-x.
依题意可列方程
x(14-x)=33,
解得x1=3,x2=11,
两个未知量怎么办
新课练习
3.两个相邻偶数的积是168.求这两个偶数的和.
解:设较小的偶数为 x,则另一个偶数为 (x+2),
依题意,得 x(x+2)=168,解得 x1=12,x2=-14,
∴x+2=14或 x+2=-12,
∴x+(x+2)=±26.
答:这两个偶数的和为±26.
课堂总结
建立一元二次方程方程
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程方程解决实际问题的步骤有哪些?
答
课堂练习
1.有一株月季,它的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数是 73,设每个支干长出 x 个小分支,根据题意可列方程为( )
B
A.1+x+x(1+x)=73 B.1+x+x2=73
C.1+x2 =73 D.(1+x)2=73
课堂练习
2.早期,甲肝流行,传染性很强,曾有 2 人同时患上甲肝.在一天内,一人平均能传染 x 人,经过两天传染后 128 人患上甲肝,则 x 的值为( )
A.10 B.9 C.8 D.7
D
解:依题意得 2+2x+x(2+2x)=128,
解得 x1=7,x2=-9(不合题意,舍去).
故 x 的值为7.
课堂练习
3.一个多边形共有14条对角线,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
4.九(1)班同学毕业的时候,每人都必须与其他任何一位同学合照一张双人照,全班共照照片780张,则九(1)班有 人.
B
40
课堂练习
5.电脑病毒感染的传播非常快,如果开始有 6 台电脑被感染,经过两轮感染后共有 2 400 台电脑被感染. 每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染 x 台电脑.
答:每轮感染中平均一台电脑会感染19台电脑.
解得x1=19 或 x2= -21 (舍去)
依题意得 6+6x+6x (1+x) =2 400
6 (1+x)2 =2 400
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
21.3实际问题与一元二次方程(1)
传染问题
人教版九年级上册
知识回顾
1.解一元二次方程有哪些方法?
直接开平方法、配方法、公式法、因式分解法.
2.列一元二次方程解应用题的步骤?
①审题,
②设出未知数,
③找等量关系,
④列方程,
⑤解方程,
⑥验根,
⑦答.
教学目标
1.通过解决“传染问题”,体验建立方程模型解决问题的一般过程;
2.通过分析、总结,找到传染问题数量关系的通性;
3.在解决问题的过程中体会一元二次方程的数学模型作用,增强应用意识和应用能力。
新知导入
若一人患流感,每轮能传染5个人,则第一轮过后共有 个人患了流感,第二轮过后共有 个人患了流感.
6
36
分析:
新知探究
探究1:有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
第1轮传染后患病人数_______人;
举例分析法:
1.如果每轮每人传染2人.
第2轮传染后患病人数 人.
第2轮
第1轮
如果每轮每人传染3人呢?
1+2=3
1+2+6=9
1+3=4
1+3+12=16
新知探究
分析 :设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
第2轮
小明
1
2
x
第1轮
小明
注意:不要忽视小明的二次传染
第1轮传染后患病人数_______人;
第2轮传染后患病人数______________人.
列表可得
[1+x+(1+x)x]
(1+x)
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
新知探究
x1= , x2= .
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去)
10
解:设每轮传染中平均一个人传染了x个人.
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,所以一定要进行检验.
例1 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
设
列
解
检
答
新知探究
传染源 新增患者人数 本轮结束患者总人数
第一轮 1 1 x=x 1+x
第二轮 1+x (1+x)x 1+x+(1+x)x=
第三轮
第n轮
思考:如果按这样的传染速度, n轮后传染后有多少人患了流感
(1+x)n
经过n轮传染后共有(1+x)n人患流感.
(1+x)2
(1+x)2 x
(1+x)2+(1+x)2 x =
(1+x)3
(1+x)2
如果按照这样的传染速度,三轮传染后有多少人患流感
若最终有b人患流感,则(1+x)n=b人患流感.
(1+x)2+(1+x)2 x =121+121×10=1331人 或 (10+1)3=1331
新知小结
传染类型关键问题
1.患者 (传染源)只参与一轮的传染还是每轮都一直在传染
2.每一轮有多少人 (传染源)在传染
3.每轮新增多少患者
4.累计患者总数是多少
新知小结
传染问题的数量关系
(传染源每轮都一直在传染)
a(x+1)n=b
原有量(a)-------传播前的数量
传播速度(x)-------一个传播多少个
轮数(n)-------传播多少轮
最终量(b)-------经过传播后的数量
新知练习
1.某种电脑病毒传播非常快,如果有一台电脑被感染,经过两轮感染后就会有81台电脑被感染。请解释:每轮感染中平均一台电脑会感染几台电脑 若病毒得不到有效控制,三轮感染后,被感染的电脑会不会超过700台
解:设平均一台电脑会感染 x 台电脑,依题意得
(x+1)2=81
x1= , x2= .
解得
-10
(不合题意,舍去)
8
第三轮感染中被感染的电脑台数为:
答:每轮感染中平均一台电脑会感染8台电脑,若病毒得不到有效控制,三轮感染后,被感染的电脑会超过700台。
(1+8)3=729>700
a(x+1)n=b
原有量(a)-------1
传播速度(x)-------x
轮数(n)-------2
最终量(b)-------81
新知探究
例2 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
主干
解:设主干长出x个支干,则每个支干长也出 x个小分支。
新知探究
例2 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支
解:设主干长出x个支干,则每个支干长也出 x个小分支。
1+x+x2=91
整理得,
x2+x-90=0
x1=9,x2=-10(不合题意,舍去)
解得,
答:每个支干长出9个小分支。
设
列
解
检
答
审
新知探究
1.分析例1和例2中的数量关系,它们有何联系和区别
交流讨论
例2 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支
例1 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
联系:表格梳理
(1+x)2=121
1+x+x2=91
区别:
每名患者每轮都传染
即传染源参加每一轮的传染
每个支干只长一次
即传染源只参加一轮的传染
新知探究
交流讨论
例1和例2的联系和区别:
传染源参加每一轮的传染
传染源只参加一轮的传染
新知探究
交流讨论
2.解决传染问题有什么分析技巧?
(1)可利用图形或表格梳理数量关系
(2) 关注起始值、新增数量、轮数和最终量,找出变化规律.
新知探究
你若和班级所有同学都握手,你需握手多少次?
例3 在某次聚会上,每两人都握了一次手,所有人共握手10次,求有多少人参加这次聚会.
新知探究
设有x个人参加这次聚会,
思考:
1.则每个人与 人握手;
2.全班共握手 次(用含有x的式子表示);
3.依题意,可列方程为:_______________________.
( x - 1 )
新知探究
例3 在某次聚会上,每两人都握了一次手,所有人共握手10次,求有多少人参加这次聚会.
解:设有x个人参加这次聚会,
x1= , x2= .
解得
-4
(不合题意,舍去)
5
答:有5人参加这次聚会.
新知练习
2.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有飞机场( )
A.4个 B.5个 C.6个 D.7个
思考:
设这个航空公司共有飞机场x个,
1.则每个机场开辟 条航线;
2.所有机场共开辟 条航线(用含有x的式子表示);
3.依题意,可列方程为:_____________.
( x - 1 )
B
新知典例
例4 两个数的和是14,积是33,求这两个数.
答:这两个数分别为3,11.
解:设其中一个数为x,则另一个数为14-x.
依题意可列方程
x(14-x)=33,
解得x1=3,x2=11,
两个未知量怎么办
新课练习
3.两个相邻偶数的积是168.求这两个偶数的和.
解:设较小的偶数为 x,则另一个偶数为 (x+2),
依题意,得 x(x+2)=168,解得 x1=12,x2=-14,
∴x+2=14或 x+2=-12,
∴x+(x+2)=±26.
答:这两个偶数的和为±26.
课堂总结
建立一元二次方程方程
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程方程解决实际问题的步骤有哪些?
答
课堂练习
1.有一株月季,它的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数是 73,设每个支干长出 x 个小分支,根据题意可列方程为( )
B
A.1+x+x(1+x)=73 B.1+x+x2=73
C.1+x2 =73 D.(1+x)2=73
课堂练习
2.早期,甲肝流行,传染性很强,曾有 2 人同时患上甲肝.在一天内,一人平均能传染 x 人,经过两天传染后 128 人患上甲肝,则 x 的值为( )
A.10 B.9 C.8 D.7
D
解:依题意得 2+2x+x(2+2x)=128,
解得 x1=7,x2=-9(不合题意,舍去).
故 x 的值为7.
课堂练习
3.一个多边形共有14条对角线,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
4.九(1)班同学毕业的时候,每人都必须与其他任何一位同学合照一张双人照,全班共照照片780张,则九(1)班有 人.
B
40
课堂练习
5.电脑病毒感染的传播非常快,如果开始有 6 台电脑被感染,经过两轮感染后共有 2 400 台电脑被感染. 每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染 x 台电脑.
答:每轮感染中平均一台电脑会感染19台电脑.
解得x1=19 或 x2= -21 (舍去)
依题意得 6+6x+6x (1+x) =2 400
6 (1+x)2 =2 400
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
