人教版2023年八年级上册第11章《三角形》单元检测卷 (含解析)
文档属性
| 名称 | 人教版2023年八年级上册第11章《三角形》单元检测卷 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 536.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 15:37:48 | ||
图片预览



文档简介
人教版2023年八年级上册第11章《三角形》单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中具有稳定性的是( )
A.六边形 B.五边形 C.四边形 D.三角形
2.下列各图中,正确画出AC边上的高的是( )
A. B. C. D.
3.下列长度的三条线段,能组成三角形的是( )
A.1,3,4 B.2,2,7 C.4,5,7 D.3,3,6
4.正十二边形的外角和为( )
A.30° B.150° C.360° D.1800°
5.在△ABC中∠A=10°,∠B=60°,则△ABC的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
6.如图,∠BCD为△ABC的外角,∠A=64°,∠BCD=142°,那么∠B=( )
A.60° B.82° C.78° D.80°
7.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
8.如图,在△ABC中,∠B=90°,若按图中虚线剪去∠B,则∠1+∠2等于( )
A.90° B.135° C.315° D.270°
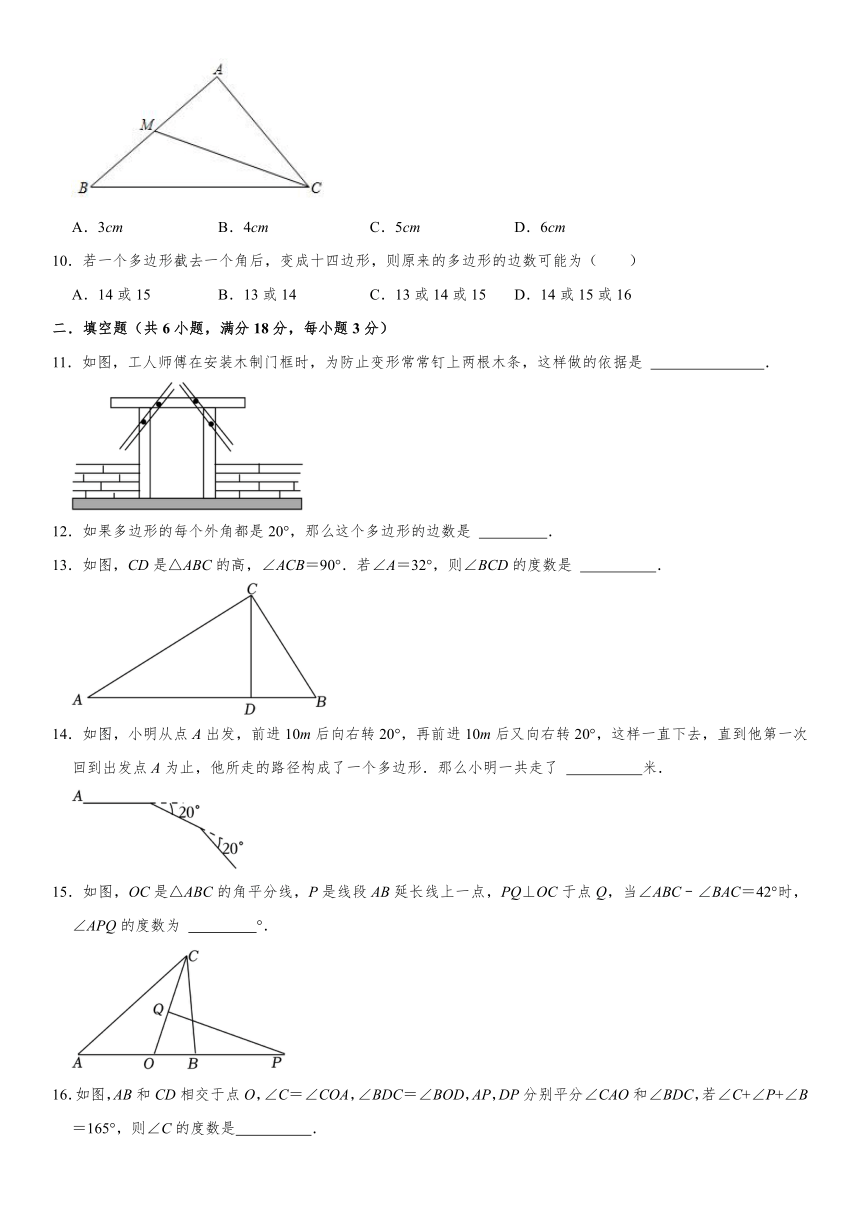
9.如图,CM是△ABC的中线,△BCM的周长比△ACM的周长大3cm,BC=8cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
10.若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为( )
A.14或15 B.13或14 C.13或14或15 D.14或15或16
二.填空题(共6小题,满分18分,每小题3分)
11.如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是 .
12.如果多边形的每个外角都是20°,那么这个多边形的边数是 .
13.如图,CD是△ABC的高,∠ACB=90°.若∠A=32°,则∠BCD的度数是 .
14.如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.那么小明一共走了 米.
15.如图,OC是△ABC的角平分线,P是线段AB延长线上一点,PQ⊥OC于点Q,当∠ABC﹣∠BAC=42°时,∠APQ的度数为 °.
16.如图,AB和CD相交于点O,∠C=∠COA,∠BDC=∠BOD,AP,DP分别平分∠CAO和∠BDC,若∠C+∠P+∠B=165°,则∠C的度数是 .
三.解答题(共7小题,满分52分)
17.(6分)如果一个正多边形的每个外角都为45°.
(1)求这个正多边形的边数;
(2)若截去一个角(截线不经过多边形的顶点),求截完角后所形成的另一个多边形的内角和.
18.(6分)AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
19.(6分)已知在△ABC中,∠A、∠B、∠C的对边分别为a、b、c.
(1)化简代数式:|a+b﹣c|+|b﹣a﹣c|= .
(2)若AB=AC,AC边上的中线BD把三角形的周长分为15和6两部分,求腰长AB.
20.(8分)如图,已知:AD平分∠BAC,点F是AD反向延长线上的一点,EF⊥BC,∠1=40°,∠C=60°,求∠B和∠F的度数.
21.(8分)如图,在△ABC中,∠B的平分线与∠ACE的平分线交于点D,求证:∠D=∠A.
22.(8分)如图,将△ABC纸片沿DE折叠,使点A落在点A'处,若∠1=80°,∠2=24°,求∠A的度数.
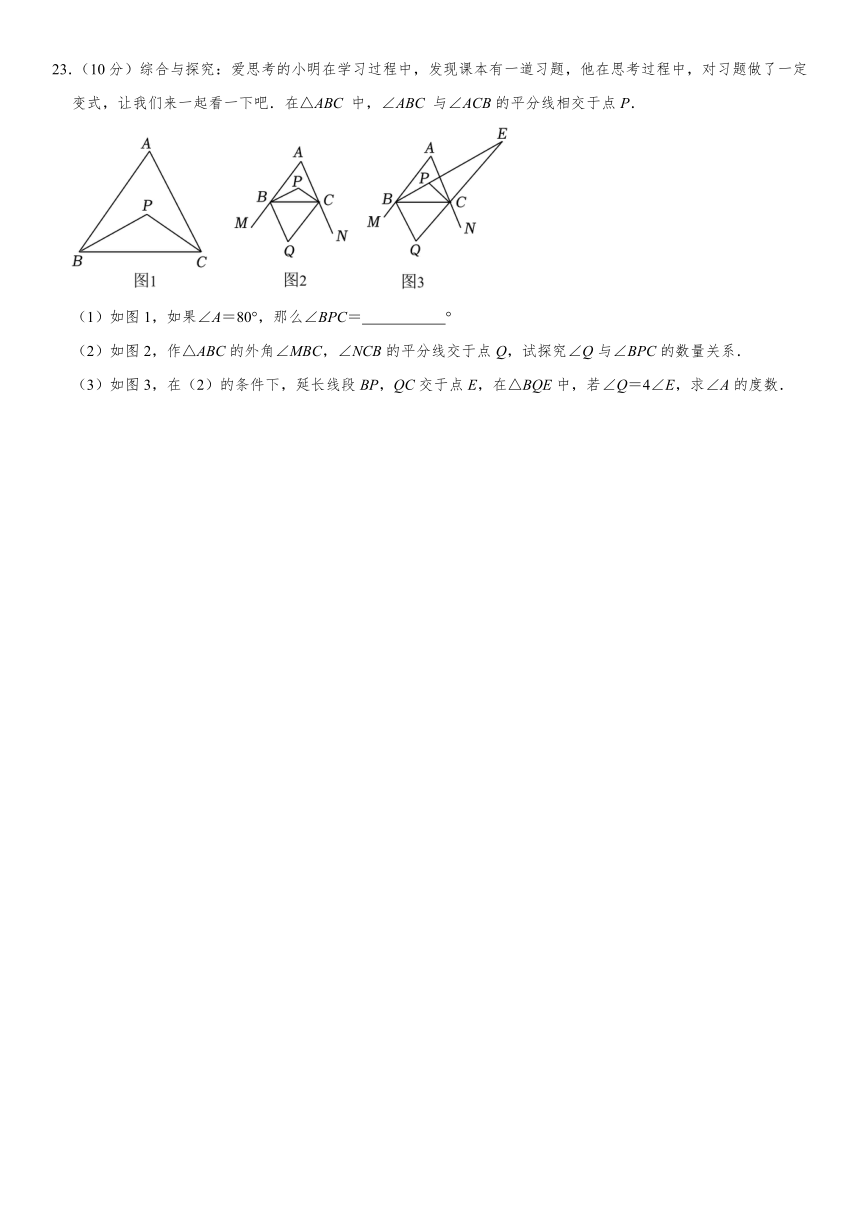
23.(10分)综合与探究:爱思考的小明在学习过程中,发现课本有一道习题,他在思考过程中,对习题做了一定变式,让我们来一起看一下吧.在△ABC 中,∠ABC 与∠ACB的平分线相交于点P.
(1)如图1,如果∠A=80°,那么∠BPC= °
(2)如图2,作△ABC的外角∠MBC,∠NCB的平分线交于点Q,试探究∠Q与∠BPC的数量关系.
(3)如图3,在(2)的条件下,延长线段BP,QC交于点E,在△BQE中,若∠Q=4∠E,求∠A的度数.
人教版2023年八年级上册第11章《三角形》单元检测卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中具有稳定性的是( )
A.六边形 B.五边形 C.四边形 D.三角形
【分析】根据三角形具有稳定性,其他多边形具有不稳定性可得结论.
【解答】解:三角形具有稳定性;
故选:D.
2.下列各图中,正确画出AC边上的高的是( )
A. B.
C. D.
【分析】根据三角形高的定义判断即可得到答案.
【解答】解:△ABC中AC边上的高即为过点B作AC的垂线段,该垂线段即为AC边上的高,四个选项中只有选项D符合题意,
故选:D.
3.下列长度的三条线段,能组成三角形的是( )
A.1,3,4 B.2,2,7 C.4,5,7 D.3,3,6
【分析】根据三角形的三边关系分别判断即可.
【解答】解:∵1+3=4,
∴1,3,4不能组成三角形,
故A选项不符合题意;
∵2+2<7,
∴2,2,7不能组成三角形,
故B不符合题意;
∵4+5>7,
∴4,5,7能组成三角形,
故C符合题意;
∵3+3=6,
∴3,3,6不能组成三角形,
故D不符合题意,
故选:C.
4.正十二边形的外角和为( )
A.30° B.150° C.360° D.1800°
【分析】本题考查多边形的外角和问题,多边形外角和定理:任意多边形的外角和都等于360°.
【解答】解:因为多边形的外角和为360°,所以正十二边形的外角和为:360°.故选:C.
5.在△ABC中∠A=10°,∠B=60°,则△ABC的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
【分析】根据三角形的内角和定理求出∠C,即可判定△ABC的形状.
【解答】解:∵∠A=10°,∠B=60°,
∴∠C=180°﹣∠A﹣∠B=180°﹣10°﹣60°=110°,
∴△ABC是钝角三角形.
故选:A.
6.如图,∠BCD为△ABC的外角,∠A=64°,∠BCD=142°,那么∠B=( )
A.60° B.82° C.78° D.80°
【分析】利用三角形的外角性质即可求解.
【解答】解:∵∠A=64°,∠BCD=142°,∠BCD是△ABC的外角,
∴∠B=∠BCD﹣∠A=78°.
故选:C.
7.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
【分析】根据三角形的定义,找出图中所有的三角形,数出其个数即可得出结论.
【解答】解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
8.如图,在△ABC中,∠B=90°,若按图中虚线剪去∠B,则∠1+∠2等于( )
A.90° B.135° C.315° D.270°
【分析】如图,根据题意可知∠1=90°+∠BNM,∠2=90°+∠BMN,然后结合三角形内角和定理即可推出∠1+∠2的度数.
【解答】解:如图.∵△ABC为直角三角形,∠B=90°,
∴∠BNM+∠BMN=90°,
∵∠1=90°+∠BNM,∠2=90°+∠BMN,
∴∠1+∠2=90°+∠BNM+90°+∠BMN=270°.
故选:D.
9.如图,CM是△ABC的中线,△BCM的周长比△ACM的周长大3cm,BC=8cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
【分析】根据三角形中线的特点进行解答即可.
【解答】解:∵CM为△ABC的AB边上的中线,
∴AM=BM,
∵△BCM的周长比△ACM的周长大3cm,
∴(BC+BM+CM)﹣(AC+AM+CM)=3cm,
∴BC﹣AC=3cm,
∵BC=8cm,
∴AC=5cm,
故选:C.
10.若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为( )
A.14或15 B.13或14 C.13或14或15 D.14或15或16
【分析】根据不同的截法,找出前后的多边形的边数之间的关系得出答案.
【解答】解:如图,n边形,A1A2A3…An,
若沿着直线A1A3截去一个角,所得到的多边形,比原来的多边形的边数少1,
若沿着直线A1M截去一个角,所得到的多边形,与原来的多边形的边数相等,
若沿着直线MN截去一个角,所得到的多边形,比原来的多边形的边数多1,
因此将一个多边形截去一个角后,变成十四边形,则原来的多边形的边数为13或14或15,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是 三角形具有稳定性 .
【分析】根据三角形具有稳定性解答即可.
【解答】解:工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是三角形具有稳定性,
故答案为:三角形具有稳定性.
12.如果多边形的每个外角都是20°,那么这个多边形的边数是 18 .
【分析】根据多边形的外角和是360度即可求得外角的个数,即多边形的边数.
【解答】解:多边形的边数是:=18,
故答案为:18.
13.如图,CD是△ABC的高,∠ACB=90°.若∠A=32°,则∠BCD的度数是 32° .
【分析】根据同角的余角相等,即可求解.
【解答】解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD是△ABC的高,
即CD⊥AB,
∴∠ADB=90°,
∴∠ACD+∠A=90°,
∴∠BCD=∠A=32°,
故答案为:32°.
14.如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.那么小明一共走了 180 米.
【分析】第一次回到出发点A时,所经过的路线正好构成一个外角是20度的正多边形,求得正多边形的边数,进而求得小明走的路程即可.
【解答】解:∵所经过的路线正好构成一个外角是20度的正多边形,
∴360÷20=18,
∵18×10=180(米),
∴淇淇一共走了180米,
故答案为:180.
15.如图,OC是△ABC的角平分线,P是线段AB延长线上一点,PQ⊥OC于点Q,当∠ABC﹣∠BAC=42°时,∠APQ的度数为 21 °.
【分析】根据三角形内角和定理、角平分线的定义以及垂直的定义进行计算即可.
【解答】解:设∠BAC=x°,则∠ABC=(x+42)°,
∴∠ACB=180°﹣x°﹣(x+42)°=(138﹣2x)°,
∵OC平分∠ACB,
∴∠ACO=∠ACB=(69﹣x)°,
∴∠POQ=∠A+∠ACO=69°,
∵PQ⊥OC,
∴∠PQO=90°,
∴∠APQ=90°﹣69°=21°,
故答案为:21.
16.如图,AB和CD相交于点O,∠C=∠COA,∠BDC=∠BOD,AP,DP分别平分∠CAO和∠BDC,若∠C+∠P+∠B=165°,则∠C的度数是 70° .
【分析】设∠C=∠AOC=∠BOD=∠BDO=x,∠CAP=∠PAB=y,∠P=z,则∠B=2y,构建方程组解决问题即可.
【解答】解:∵∠C=∠COA,∠BDC=∠BOD,∠AOC=∠BOD,
∴∠C=∠AOC=∠BOD=∠BDO,
∴∠B=∠CAO,设∠C=∠AOC=∠BOD=∠BDO=x,∠CAP=∠PAB=y,∠P=z,则∠B=2y,
则有,
解得,
∴∠C=70°,
故答案为70°.
三.解答题(共7小题,满分52分)
17.(6分)如果一个正多边形的每个外角都为45°.
(1)求这个正多边形的边数;
(2)若截去一个角(截线不经过多边形的顶点),求截完角后所形成的另一个多边形的内角和.
【分析】(1)利用正多边形的性质和多边形的外角和计算即可;
(2)由题意确定截完角后所形成多边形的边数,然后利用多边形的内角和公式计算即可.
【解答】解:(1)由题意可得:360°÷45°=8,
即这个正多边形的边数为8;
(2)∵将正多边形截去一个角(截线不经过多边形的顶点),
∴截完角后所形成的多边形为九边形,
则其内角和为:(9﹣2)×180°=1260°.
18.(6分)AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
【分析】根据同角的余角相等求出∠BHD=∠C,从而得解.
【解答】解:∵AD是△ABC的高,
∴∠BHD+∠HBD=90°,
∵BE是△ABC的高,
∴∠HBD+∠C=90°,
∴∠BHD=∠C,
∵∠C=50°,
∴∠BHD=50°.
19.(6分)已知在△ABC中,∠A、∠B、∠C的对边分别为a、b、c.
(1)化简代数式:|a+b﹣c|+|b﹣a﹣c|= 2a .
(2)若AB=AC,AC边上的中线BD把三角形的周长分为15和6两部分,求腰长AB.
【分析】(1)先根据三角形的三边关系定理可得a+b>c,a+c>b,从而可得a+b﹣c>0,b﹣a﹣c<0,再化简绝对值,然后计算整式的加减法即可得;
(2)先根据三角形中线的定义可得,再分①和②两种情况,分别求出a,c的值,从而可得三角形的三边长,然后看是否符合三角形的三边关系定理即可得出答案.
【解答】解:(1)由题意得:a+b>c,a+c>b,
∴a+b﹣c>0,b﹣a﹣c<0,
∴|a+b﹣c|+|b﹣a﹣c|
=a+b﹣c+(﹣b+a+c)
=a+b﹣c﹣b+a+c
=2a.
故答案为:2a;
(2)设AB=AC=2x,BC=y,则AD=CD=x,
∵AC上的中线BD将这个三角形的周长分成15和6两部分,
①当3x=15,且x+y=6,
解得,x=5,y=1,
∴三边长分别为10,10,1;
②当x+y=15且3x=6时,
解得,x=2,y=13,此时腰为4,
根据三角形三边关系,任意两边之和大于第三边,而4+4=8<13,故这种情况不存在.
∴△ABC的腰长AB为10.
20.(8分)如图,已知:AD平分∠BAC,点F是AD反向延长线上的一点,EF⊥BC,∠1=40°,∠C=60°,求∠B和∠F的度数.
【分析】先利用角平分线的性质和三角形的内角和定理求出∠B,再利用外角和内角的关系求出∠CDF,最后利用三角形的内角和定理求出∠F.
【解答】解:∵AD平分∠BAC,∠1=40°,
∴∠BAC=2∠1=80°.
∵∠C=60°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣80°﹣60°=40°.
∴∠EDF=∠B+∠1=40°+40°=80°.
∵EF⊥BC,
∴∠DEF=90°.
∴在Rt△EDF中,∠F=90°﹣∠EDF=90°﹣80°=10°.
21.(8分)如图,在△ABC中,∠B的平分线与∠ACE的平分线交于点D,求证:∠D=∠A.
【分析】先通过角平分线的性质得到∠DCE与∠ACE、∠DBC与∠ABC间关系,再利用三角形的外角和内角的关系得结论.
【解答】证明:∵∠ACE=∠A+∠ABC,CD是∠ACE的平分线,
∴∠DCE=∠ACE=(∠A+∠ABC)=A+ABC.
∵∠DCE=∠DBC+∠D,
∴∠D=∠DCE﹣∠DBC.
∵BD是∠ABC的平分线,
∴∠DBC=∠ABC.
∴∠D=∠DCE﹣∠DBC
=A+ABC﹣ABC
=..
22.(8分)如图,将△ABC纸片沿DE折叠,使点A落在点A'处,若∠1=80°,∠2=24°,求∠A的度数.
【分析】由图可知∠1是△ADF的外角,根据三角形外角的性质可得∠A+∠AFD=∠1;∠AFD是△EFA'的外角,同理可得∠2+∠A'=∠AFD,则∠A+∠2+∠A'=∠1,由折叠可知∠A=∠A',将∠1、∠2的度数带入,即可求出∠A的度数.
【解答】解:如图所示:
∵∠1是△ADF的外角,
∴∠A+∠AFD=∠1;
又∵∠AFD是△EFA'的外角,
∴∠2+∠A'=∠AFD,
∴∠A+∠2+∠A'=∠1,
由折叠可知∠A=∠A',且∠1=80°,∠2=24°,
∴∠A+24°+∠A=80°,
即:2∠A=56°,
解得:∠A=28°.
23.(10分)综合与探究:爱思考的小明在学习过程中,发现课本有一道习题,他在思考过程中,对习题做了一定变式,让我们来一起看一下吧.在△ABC 中,∠ABC 与∠ACB的平分线相交于点P.
(1)如图1,如果∠A=80°,那么∠BPC= 130° °
(2)如图2,作△ABC的外角∠MBC,∠NCB的平分线交于点Q,试探究∠Q与∠BPC的数量关系.
(3)如图3,在(2)的条件下,延长线段BP,QC交于点E,在△BQE中,若∠Q=4∠E,求∠A的度数.
【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠ABC+∠ACB,进而求出∠BPC即可解决问题;
(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解;
(3)在△BQE中,由于∠Q=90°﹣∠A,求出∠E=∠A,由∠Q=4∠E,得出2∠A=90°﹣∠A,求解即可.
【解答】解:(1)∵∠A=80°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣8°=100°,
∵∠ABC与∠ACB的平分线交于点P,
∴,,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=180=130°;
故答案为:130°;
(2)∵外角∠MBC,∠NCB的平分线交于点Q,
∴,.
∴∠Q=180°﹣(∠QBC+∠QCB)=180°﹣(∠MBC+∠NCB)=180°﹣(180°﹣∠ABC+180°﹣∠ACB)=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣,
∵∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+,
∴∠Q+∠BPC=180°;
(3)如图,延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A,
∵∠Q=4∠E,
∴∠Q=2∠A,
∵∠Q=90°﹣∠A,
∴2∠A=90°﹣∠A,
∴∠A=36°.
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中具有稳定性的是( )
A.六边形 B.五边形 C.四边形 D.三角形
2.下列各图中,正确画出AC边上的高的是( )
A. B. C. D.
3.下列长度的三条线段,能组成三角形的是( )
A.1,3,4 B.2,2,7 C.4,5,7 D.3,3,6
4.正十二边形的外角和为( )
A.30° B.150° C.360° D.1800°
5.在△ABC中∠A=10°,∠B=60°,则△ABC的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
6.如图,∠BCD为△ABC的外角,∠A=64°,∠BCD=142°,那么∠B=( )
A.60° B.82° C.78° D.80°
7.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
8.如图,在△ABC中,∠B=90°,若按图中虚线剪去∠B,则∠1+∠2等于( )
A.90° B.135° C.315° D.270°
9.如图,CM是△ABC的中线,△BCM的周长比△ACM的周长大3cm,BC=8cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
10.若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为( )
A.14或15 B.13或14 C.13或14或15 D.14或15或16
二.填空题(共6小题,满分18分,每小题3分)
11.如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是 .
12.如果多边形的每个外角都是20°,那么这个多边形的边数是 .
13.如图,CD是△ABC的高,∠ACB=90°.若∠A=32°,则∠BCD的度数是 .
14.如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.那么小明一共走了 米.
15.如图,OC是△ABC的角平分线,P是线段AB延长线上一点,PQ⊥OC于点Q,当∠ABC﹣∠BAC=42°时,∠APQ的度数为 °.
16.如图,AB和CD相交于点O,∠C=∠COA,∠BDC=∠BOD,AP,DP分别平分∠CAO和∠BDC,若∠C+∠P+∠B=165°,则∠C的度数是 .
三.解答题(共7小题,满分52分)
17.(6分)如果一个正多边形的每个外角都为45°.
(1)求这个正多边形的边数;
(2)若截去一个角(截线不经过多边形的顶点),求截完角后所形成的另一个多边形的内角和.
18.(6分)AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
19.(6分)已知在△ABC中,∠A、∠B、∠C的对边分别为a、b、c.
(1)化简代数式:|a+b﹣c|+|b﹣a﹣c|= .
(2)若AB=AC,AC边上的中线BD把三角形的周长分为15和6两部分,求腰长AB.
20.(8分)如图,已知:AD平分∠BAC,点F是AD反向延长线上的一点,EF⊥BC,∠1=40°,∠C=60°,求∠B和∠F的度数.
21.(8分)如图,在△ABC中,∠B的平分线与∠ACE的平分线交于点D,求证:∠D=∠A.
22.(8分)如图,将△ABC纸片沿DE折叠,使点A落在点A'处,若∠1=80°,∠2=24°,求∠A的度数.
23.(10分)综合与探究:爱思考的小明在学习过程中,发现课本有一道习题,他在思考过程中,对习题做了一定变式,让我们来一起看一下吧.在△ABC 中,∠ABC 与∠ACB的平分线相交于点P.
(1)如图1,如果∠A=80°,那么∠BPC= °
(2)如图2,作△ABC的外角∠MBC,∠NCB的平分线交于点Q,试探究∠Q与∠BPC的数量关系.
(3)如图3,在(2)的条件下,延长线段BP,QC交于点E,在△BQE中,若∠Q=4∠E,求∠A的度数.
人教版2023年八年级上册第11章《三角形》单元检测卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中具有稳定性的是( )
A.六边形 B.五边形 C.四边形 D.三角形
【分析】根据三角形具有稳定性,其他多边形具有不稳定性可得结论.
【解答】解:三角形具有稳定性;
故选:D.
2.下列各图中,正确画出AC边上的高的是( )
A. B.
C. D.
【分析】根据三角形高的定义判断即可得到答案.
【解答】解:△ABC中AC边上的高即为过点B作AC的垂线段,该垂线段即为AC边上的高,四个选项中只有选项D符合题意,
故选:D.
3.下列长度的三条线段,能组成三角形的是( )
A.1,3,4 B.2,2,7 C.4,5,7 D.3,3,6
【分析】根据三角形的三边关系分别判断即可.
【解答】解:∵1+3=4,
∴1,3,4不能组成三角形,
故A选项不符合题意;
∵2+2<7,
∴2,2,7不能组成三角形,
故B不符合题意;
∵4+5>7,
∴4,5,7能组成三角形,
故C符合题意;
∵3+3=6,
∴3,3,6不能组成三角形,
故D不符合题意,
故选:C.
4.正十二边形的外角和为( )
A.30° B.150° C.360° D.1800°
【分析】本题考查多边形的外角和问题,多边形外角和定理:任意多边形的外角和都等于360°.
【解答】解:因为多边形的外角和为360°,所以正十二边形的外角和为:360°.故选:C.
5.在△ABC中∠A=10°,∠B=60°,则△ABC的形状是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
【分析】根据三角形的内角和定理求出∠C,即可判定△ABC的形状.
【解答】解:∵∠A=10°,∠B=60°,
∴∠C=180°﹣∠A﹣∠B=180°﹣10°﹣60°=110°,
∴△ABC是钝角三角形.
故选:A.
6.如图,∠BCD为△ABC的外角,∠A=64°,∠BCD=142°,那么∠B=( )
A.60° B.82° C.78° D.80°
【分析】利用三角形的外角性质即可求解.
【解答】解:∵∠A=64°,∠BCD=142°,∠BCD是△ABC的外角,
∴∠B=∠BCD﹣∠A=78°.
故选:C.
7.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
【分析】根据三角形的定义,找出图中所有的三角形,数出其个数即可得出结论.
【解答】解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
8.如图,在△ABC中,∠B=90°,若按图中虚线剪去∠B,则∠1+∠2等于( )
A.90° B.135° C.315° D.270°
【分析】如图,根据题意可知∠1=90°+∠BNM,∠2=90°+∠BMN,然后结合三角形内角和定理即可推出∠1+∠2的度数.
【解答】解:如图.∵△ABC为直角三角形,∠B=90°,
∴∠BNM+∠BMN=90°,
∵∠1=90°+∠BNM,∠2=90°+∠BMN,
∴∠1+∠2=90°+∠BNM+90°+∠BMN=270°.
故选:D.
9.如图,CM是△ABC的中线,△BCM的周长比△ACM的周长大3cm,BC=8cm,则AC的长为( )
A.3cm B.4cm C.5cm D.6cm
【分析】根据三角形中线的特点进行解答即可.
【解答】解:∵CM为△ABC的AB边上的中线,
∴AM=BM,
∵△BCM的周长比△ACM的周长大3cm,
∴(BC+BM+CM)﹣(AC+AM+CM)=3cm,
∴BC﹣AC=3cm,
∵BC=8cm,
∴AC=5cm,
故选:C.
10.若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为( )
A.14或15 B.13或14 C.13或14或15 D.14或15或16
【分析】根据不同的截法,找出前后的多边形的边数之间的关系得出答案.
【解答】解:如图,n边形,A1A2A3…An,
若沿着直线A1A3截去一个角,所得到的多边形,比原来的多边形的边数少1,
若沿着直线A1M截去一个角,所得到的多边形,与原来的多边形的边数相等,
若沿着直线MN截去一个角,所得到的多边形,比原来的多边形的边数多1,
因此将一个多边形截去一个角后,变成十四边形,则原来的多边形的边数为13或14或15,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.如图,工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是 三角形具有稳定性 .
【分析】根据三角形具有稳定性解答即可.
【解答】解:工人师傅在安装木制门框时,为防止变形常常钉上两根木条,这样做的依据是三角形具有稳定性,
故答案为:三角形具有稳定性.
12.如果多边形的每个外角都是20°,那么这个多边形的边数是 18 .
【分析】根据多边形的外角和是360度即可求得外角的个数,即多边形的边数.
【解答】解:多边形的边数是:=18,
故答案为:18.
13.如图,CD是△ABC的高,∠ACB=90°.若∠A=32°,则∠BCD的度数是 32° .
【分析】根据同角的余角相等,即可求解.
【解答】解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD是△ABC的高,
即CD⊥AB,
∴∠ADB=90°,
∴∠ACD+∠A=90°,
∴∠BCD=∠A=32°,
故答案为:32°.
14.如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.那么小明一共走了 180 米.
【分析】第一次回到出发点A时,所经过的路线正好构成一个外角是20度的正多边形,求得正多边形的边数,进而求得小明走的路程即可.
【解答】解:∵所经过的路线正好构成一个外角是20度的正多边形,
∴360÷20=18,
∵18×10=180(米),
∴淇淇一共走了180米,
故答案为:180.
15.如图,OC是△ABC的角平分线,P是线段AB延长线上一点,PQ⊥OC于点Q,当∠ABC﹣∠BAC=42°时,∠APQ的度数为 21 °.
【分析】根据三角形内角和定理、角平分线的定义以及垂直的定义进行计算即可.
【解答】解:设∠BAC=x°,则∠ABC=(x+42)°,
∴∠ACB=180°﹣x°﹣(x+42)°=(138﹣2x)°,
∵OC平分∠ACB,
∴∠ACO=∠ACB=(69﹣x)°,
∴∠POQ=∠A+∠ACO=69°,
∵PQ⊥OC,
∴∠PQO=90°,
∴∠APQ=90°﹣69°=21°,
故答案为:21.
16.如图,AB和CD相交于点O,∠C=∠COA,∠BDC=∠BOD,AP,DP分别平分∠CAO和∠BDC,若∠C+∠P+∠B=165°,则∠C的度数是 70° .
【分析】设∠C=∠AOC=∠BOD=∠BDO=x,∠CAP=∠PAB=y,∠P=z,则∠B=2y,构建方程组解决问题即可.
【解答】解:∵∠C=∠COA,∠BDC=∠BOD,∠AOC=∠BOD,
∴∠C=∠AOC=∠BOD=∠BDO,
∴∠B=∠CAO,设∠C=∠AOC=∠BOD=∠BDO=x,∠CAP=∠PAB=y,∠P=z,则∠B=2y,
则有,
解得,
∴∠C=70°,
故答案为70°.
三.解答题(共7小题,满分52分)
17.(6分)如果一个正多边形的每个外角都为45°.
(1)求这个正多边形的边数;
(2)若截去一个角(截线不经过多边形的顶点),求截完角后所形成的另一个多边形的内角和.
【分析】(1)利用正多边形的性质和多边形的外角和计算即可;
(2)由题意确定截完角后所形成多边形的边数,然后利用多边形的内角和公式计算即可.
【解答】解:(1)由题意可得:360°÷45°=8,
即这个正多边形的边数为8;
(2)∵将正多边形截去一个角(截线不经过多边形的顶点),
∴截完角后所形成的多边形为九边形,
则其内角和为:(9﹣2)×180°=1260°.
18.(6分)AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
【分析】根据同角的余角相等求出∠BHD=∠C,从而得解.
【解答】解:∵AD是△ABC的高,
∴∠BHD+∠HBD=90°,
∵BE是△ABC的高,
∴∠HBD+∠C=90°,
∴∠BHD=∠C,
∵∠C=50°,
∴∠BHD=50°.
19.(6分)已知在△ABC中,∠A、∠B、∠C的对边分别为a、b、c.
(1)化简代数式:|a+b﹣c|+|b﹣a﹣c|= 2a .
(2)若AB=AC,AC边上的中线BD把三角形的周长分为15和6两部分,求腰长AB.
【分析】(1)先根据三角形的三边关系定理可得a+b>c,a+c>b,从而可得a+b﹣c>0,b﹣a﹣c<0,再化简绝对值,然后计算整式的加减法即可得;
(2)先根据三角形中线的定义可得,再分①和②两种情况,分别求出a,c的值,从而可得三角形的三边长,然后看是否符合三角形的三边关系定理即可得出答案.
【解答】解:(1)由题意得:a+b>c,a+c>b,
∴a+b﹣c>0,b﹣a﹣c<0,
∴|a+b﹣c|+|b﹣a﹣c|
=a+b﹣c+(﹣b+a+c)
=a+b﹣c﹣b+a+c
=2a.
故答案为:2a;
(2)设AB=AC=2x,BC=y,则AD=CD=x,
∵AC上的中线BD将这个三角形的周长分成15和6两部分,
①当3x=15,且x+y=6,
解得,x=5,y=1,
∴三边长分别为10,10,1;
②当x+y=15且3x=6时,
解得,x=2,y=13,此时腰为4,
根据三角形三边关系,任意两边之和大于第三边,而4+4=8<13,故这种情况不存在.
∴△ABC的腰长AB为10.
20.(8分)如图,已知:AD平分∠BAC,点F是AD反向延长线上的一点,EF⊥BC,∠1=40°,∠C=60°,求∠B和∠F的度数.
【分析】先利用角平分线的性质和三角形的内角和定理求出∠B,再利用外角和内角的关系求出∠CDF,最后利用三角形的内角和定理求出∠F.
【解答】解:∵AD平分∠BAC,∠1=40°,
∴∠BAC=2∠1=80°.
∵∠C=60°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣80°﹣60°=40°.
∴∠EDF=∠B+∠1=40°+40°=80°.
∵EF⊥BC,
∴∠DEF=90°.
∴在Rt△EDF中,∠F=90°﹣∠EDF=90°﹣80°=10°.
21.(8分)如图,在△ABC中,∠B的平分线与∠ACE的平分线交于点D,求证:∠D=∠A.
【分析】先通过角平分线的性质得到∠DCE与∠ACE、∠DBC与∠ABC间关系,再利用三角形的外角和内角的关系得结论.
【解答】证明:∵∠ACE=∠A+∠ABC,CD是∠ACE的平分线,
∴∠DCE=∠ACE=(∠A+∠ABC)=A+ABC.
∵∠DCE=∠DBC+∠D,
∴∠D=∠DCE﹣∠DBC.
∵BD是∠ABC的平分线,
∴∠DBC=∠ABC.
∴∠D=∠DCE﹣∠DBC
=A+ABC﹣ABC
=..
22.(8分)如图,将△ABC纸片沿DE折叠,使点A落在点A'处,若∠1=80°,∠2=24°,求∠A的度数.
【分析】由图可知∠1是△ADF的外角,根据三角形外角的性质可得∠A+∠AFD=∠1;∠AFD是△EFA'的外角,同理可得∠2+∠A'=∠AFD,则∠A+∠2+∠A'=∠1,由折叠可知∠A=∠A',将∠1、∠2的度数带入,即可求出∠A的度数.
【解答】解:如图所示:
∵∠1是△ADF的外角,
∴∠A+∠AFD=∠1;
又∵∠AFD是△EFA'的外角,
∴∠2+∠A'=∠AFD,
∴∠A+∠2+∠A'=∠1,
由折叠可知∠A=∠A',且∠1=80°,∠2=24°,
∴∠A+24°+∠A=80°,
即:2∠A=56°,
解得:∠A=28°.
23.(10分)综合与探究:爱思考的小明在学习过程中,发现课本有一道习题,他在思考过程中,对习题做了一定变式,让我们来一起看一下吧.在△ABC 中,∠ABC 与∠ACB的平分线相交于点P.
(1)如图1,如果∠A=80°,那么∠BPC= 130° °
(2)如图2,作△ABC的外角∠MBC,∠NCB的平分线交于点Q,试探究∠Q与∠BPC的数量关系.
(3)如图3,在(2)的条件下,延长线段BP,QC交于点E,在△BQE中,若∠Q=4∠E,求∠A的度数.
【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠ABC+∠ACB,进而求出∠BPC即可解决问题;
(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解;
(3)在△BQE中,由于∠Q=90°﹣∠A,求出∠E=∠A,由∠Q=4∠E,得出2∠A=90°﹣∠A,求解即可.
【解答】解:(1)∵∠A=80°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣8°=100°,
∵∠ABC与∠ACB的平分线交于点P,
∴,,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=180=130°;
故答案为:130°;
(2)∵外角∠MBC,∠NCB的平分线交于点Q,
∴,.
∴∠Q=180°﹣(∠QBC+∠QCB)=180°﹣(∠MBC+∠NCB)=180°﹣(180°﹣∠ABC+180°﹣∠ACB)=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣,
∵∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+,
∴∠Q+∠BPC=180°;
(3)如图,延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A,
∵∠Q=4∠E,
∴∠Q=2∠A,
∵∠Q=90°﹣∠A,
∴2∠A=90°﹣∠A,
∴∠A=36°.
