1.2.4 绝对值(第二课时) 课件(27张PPT)
文档属性
| 名称 | 1.2.4 绝对值(第二课时) 课件(27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 11:18:24 | ||
图片预览






文档简介
(共27张PPT)
第1章 有理数
1.2.4 绝对值
第一单元
1.掌握有理数大小的比较法则;(数形结合)
2.会比较有理数的大小,并能正确地使用“>”或“<”号连接;
3.能初步进行有理数大小比较的推理和书写.
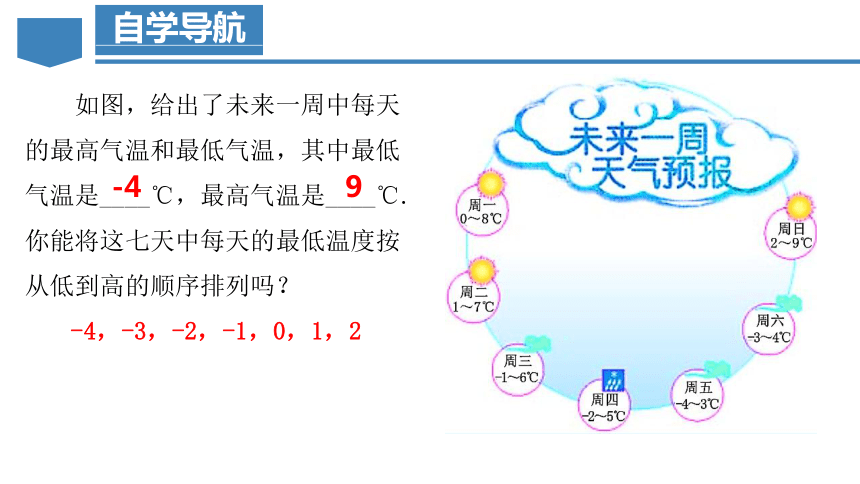
如图,给出了未来一周中每天的最高气温和最低气温,其中最低气温是____℃,最高气温是____℃. 你能将这七天中每天的最低温度按从低到高的顺序排列吗?
-4,-3,-2,-1,0,1,2
-4
9
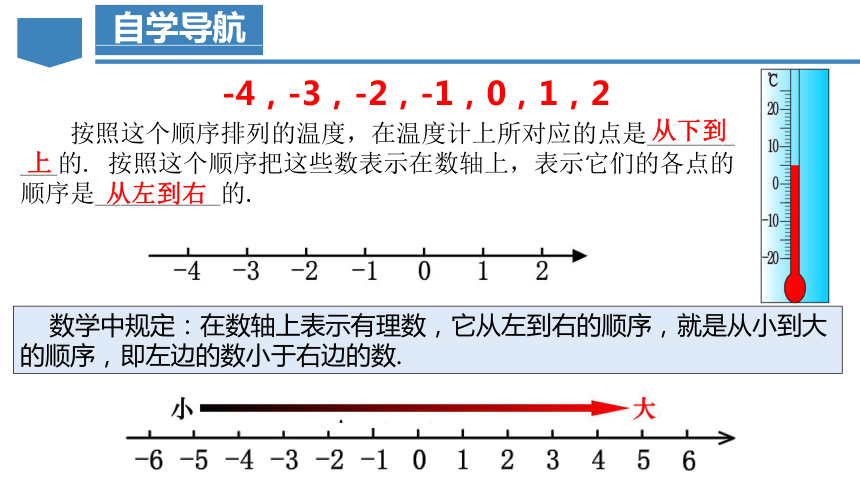
按照这个顺序排列的温度,在温度计上所对应的点是_______
___的. 按照这个顺序把这些数表示在数轴上,表示它们的各点的顺序是__________的.
-4,-3,-2,-1,0,1,2
数学中规定:在数轴上表示有理数,它从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
从左到右
从下到
上
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
有没有最大的有理数 有没有最小的有理数 为什么
借助数轴比较有理数的大小
利用数轴比较有理数的大小
重点
例1.把下列各数在数轴上表示出来,并用“<”号连接:
-,3,-4,0,-1.5,
分析:将数标在数轴上,根据数轴上的数从左到右的排列顺序比较大小.
解:画数轴并将各数表示在数轴上,如图所示:
根据数轴上左边的点表示的数总比右边的点表示的数小,用“<”号连接为
-4<-<-1.5<0<3<.
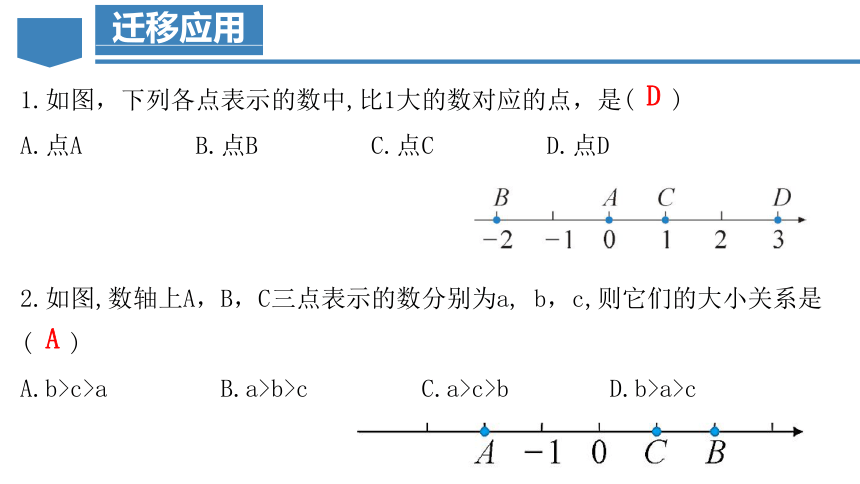
1.如图,下列各点表示的数中,比1大的数对应的点,是( )
A.点A B.点B C.点C D.点D
D
2.如图,数轴上A,B,C三点表示的数分别为a, b,c,则它们的大小关系是
( )
A.b>c>a B.a>b>c C.a>c>b D.b>a>c
A
3.将下列各数表示在数轴上,并用“<”号连接.
0,2,-(-5),-,-4.5,-2.
解:画数轴并将各数表示在数轴上,如图所示:
根据数轴上左边的点表示的数总比右边的点表示的数小,用“<”号连接为
-4.5<-| 3|<-2<0<2<-(-5).
1.对于正数、0、负数这三类数,它们之间有什么大小关系?
一般地,正数大于0,0大于负数,正数大于负数;
例如:1____0,0____-1,1____-1.
>
>
>
2.两个负数之间如何比较大小?
两个负数,绝对值大的反而小.
-3和-6如何比较大小呢?
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
运用法则比较有理数的大小
重点
例2.比较下列各对数的大小:
(1)2%与0; (2)-|-5|和0; (3)-(-0.5)与-(+0.6);
(4)-和-; (5)-和-3.13; (6)-(-)和.
解:(1)2%>0.
(2)先化简,-|-5|=-5.因为-5<0,所以-|-5|<0.
(3)先化简,-(-0.5)=0.5,-(+0.6)=-0.6.
因为0.5>-0.6,
所以-(-0.5)>-( +0.6).
运用法则比较有理数的大小
重点
例2.比较下列各对数的大小:
(1)2%与0; (2)-|-5|和0; (3)-(-0.5)与-(+0.6);
(4)-和-; (5)-和-3.13; (6)-(-)和.
解: (4)|-|==,|-|==,
因为<,即|-|<|-|,所以->-.
(5)=≈3.14,=3.13
因为3.14>3.13,即>,所以-<-3.13.
运用法则比较有理数的大小
重点
例2.比较下列各对数的大小:
(1)2%与0; (2)-|-5|和0; (3)-(-0.5)与-(+0.6);
(4)-和-; (5)-和-3.13; (6)-(-)和.
解: (6)先化简, -(-)=,=.
因为,所以-(-)>.
比较两个负数大小的方法步骤是:
(1)如果需要化简,要先进行化简;
(2)再分别求出两个负数的绝对值;
(3)比较两个绝对值的大小;
(4)根据“两个负数,绝对值大的反而小”做出正确的判断.
1.下列有理数中,最小的是( )
A. B.0 C.-0.12 D.-2
2.写出一个比-5大的负有理数:______________.
3.比较大小:(填“<”“=”“或“>”)
(1)-1____0; (2)-6____-8
>
<
-1(答案不唯一)
D
4.比较下列各对数的大小:
(1)3和|-2|; (2)-|-2.7|和-(-3.3); (3)-和-; (4)-和-1.5.
解: (1)|-|=,因为>,所以3>|-2|.
(2)-=,=3.3,
因为-2.7<3.3,所以-|-2.7|<-(-3.3).
(3)|-|==,|-|==,
因为>,即|-|>|-|,所以-<-.
4.比较下列各对数的大小:
(1)3和|-2|; (2)-|-2.7|和-(-3.3); (3)-和-; (4)-和-1.5.
解: (4)|-|==,|-|=,
因为<,即|-|<|-|,所以->-.
比较表示数的字母的大小
易错点
例3.有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.a>b B.|a|>|b| C.-a>b D.a>-b
例4.如果 ,试比较 的大小.
解:因为
所以
因为 ,
所以 ,
所以 , ,
所以 .
0
a
b
-b
-a
比较表示数的字母的大小
易错点
1.有理数a,b在数轴上的对应点的位置如图所示,下列结论正确的是( )
A.a>b B.|a|<|b| C.a>-b D.-a>b
D
2.a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,-a,b,-b按照从小到大的顺序排列为( )
A.-b<-a<a<b B.-a<-b<a<b
C.-b<a<-a<b D.-b<b<-a<a
C
例5.下表是几种液体在标准大气压下的沸点,则沸点最高的液体是( )
A.液态氧 B.液态氢
C.液态氮 D.液态氦
解析:易知-268.9<-253<-196<-183,所以液态氧的沸点最高.
A
有理数大小比较的应用
重点
1.下表是某省四个景区某天6时的气温,其中气温最低的是( )
A.石膏山 B.五台山 C.芦芽山 D.绵山
C
2.某公司抽检盒装牛奶的容量,超过标准容量的部分记为正数,不足的部分记为负数.从容量的角度看,以下四盒牛奶容量最接近标准的是( )
A. B. C. D.
【分析】解:A.+0.8的绝对值是0.8;B.-1.2的绝对值是1.2;C.-0.5的绝对值是0.5;D.+1的绝对值是1.
因为0.5<0.8<1<1.2,所以C选项的绝对值最小.
C
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
第1章 有理数
1.2.4 绝对值
第一单元
1.掌握有理数大小的比较法则;(数形结合)
2.会比较有理数的大小,并能正确地使用“>”或“<”号连接;
3.能初步进行有理数大小比较的推理和书写.
如图,给出了未来一周中每天的最高气温和最低气温,其中最低气温是____℃,最高气温是____℃. 你能将这七天中每天的最低温度按从低到高的顺序排列吗?
-4,-3,-2,-1,0,1,2
-4
9
按照这个顺序排列的温度,在温度计上所对应的点是_______
___的. 按照这个顺序把这些数表示在数轴上,表示它们的各点的顺序是__________的.
-4,-3,-2,-1,0,1,2
数学中规定:在数轴上表示有理数,它从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
从左到右
从下到
上
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
有没有最大的有理数 有没有最小的有理数 为什么
借助数轴比较有理数的大小
利用数轴比较有理数的大小
重点
例1.把下列各数在数轴上表示出来,并用“<”号连接:
-,3,-4,0,-1.5,
分析:将数标在数轴上,根据数轴上的数从左到右的排列顺序比较大小.
解:画数轴并将各数表示在数轴上,如图所示:
根据数轴上左边的点表示的数总比右边的点表示的数小,用“<”号连接为
-4<-<-1.5<0<3<.
1.如图,下列各点表示的数中,比1大的数对应的点,是( )
A.点A B.点B C.点C D.点D
D
2.如图,数轴上A,B,C三点表示的数分别为a, b,c,则它们的大小关系是
( )
A.b>c>a B.a>b>c C.a>c>b D.b>a>c
A
3.将下列各数表示在数轴上,并用“<”号连接.
0,2,-(-5),-,-4.5,-2.
解:画数轴并将各数表示在数轴上,如图所示:
根据数轴上左边的点表示的数总比右边的点表示的数小,用“<”号连接为
-4.5<-| 3|<-2<0<2<-(-5).
1.对于正数、0、负数这三类数,它们之间有什么大小关系?
一般地,正数大于0,0大于负数,正数大于负数;
例如:1____0,0____-1,1____-1.
>
>
>
2.两个负数之间如何比较大小?
两个负数,绝对值大的反而小.
-3和-6如何比较大小呢?
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
运用法则比较有理数的大小
重点
例2.比较下列各对数的大小:
(1)2%与0; (2)-|-5|和0; (3)-(-0.5)与-(+0.6);
(4)-和-; (5)-和-3.13; (6)-(-)和.
解:(1)2%>0.
(2)先化简,-|-5|=-5.因为-5<0,所以-|-5|<0.
(3)先化简,-(-0.5)=0.5,-(+0.6)=-0.6.
因为0.5>-0.6,
所以-(-0.5)>-( +0.6).
运用法则比较有理数的大小
重点
例2.比较下列各对数的大小:
(1)2%与0; (2)-|-5|和0; (3)-(-0.5)与-(+0.6);
(4)-和-; (5)-和-3.13; (6)-(-)和.
解: (4)|-|==,|-|==,
因为<,即|-|<|-|,所以->-.
(5)=≈3.14,=3.13
因为3.14>3.13,即>,所以-<-3.13.
运用法则比较有理数的大小
重点
例2.比较下列各对数的大小:
(1)2%与0; (2)-|-5|和0; (3)-(-0.5)与-(+0.6);
(4)-和-; (5)-和-3.13; (6)-(-)和.
解: (6)先化简, -(-)=,=.
因为,所以-(-)>.
比较两个负数大小的方法步骤是:
(1)如果需要化简,要先进行化简;
(2)再分别求出两个负数的绝对值;
(3)比较两个绝对值的大小;
(4)根据“两个负数,绝对值大的反而小”做出正确的判断.
1.下列有理数中,最小的是( )
A. B.0 C.-0.12 D.-2
2.写出一个比-5大的负有理数:______________.
3.比较大小:(填“<”“=”“或“>”)
(1)-1____0; (2)-6____-8
>
<
-1(答案不唯一)
D
4.比较下列各对数的大小:
(1)3和|-2|; (2)-|-2.7|和-(-3.3); (3)-和-; (4)-和-1.5.
解: (1)|-|=,因为>,所以3>|-2|.
(2)-=,=3.3,
因为-2.7<3.3,所以-|-2.7|<-(-3.3).
(3)|-|==,|-|==,
因为>,即|-|>|-|,所以-<-.
4.比较下列各对数的大小:
(1)3和|-2|; (2)-|-2.7|和-(-3.3); (3)-和-; (4)-和-1.5.
解: (4)|-|==,|-|=,
因为<,即|-|<|-|,所以->-.
比较表示数的字母的大小
易错点
例3.有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.a>b B.|a|>|b| C.-a>b D.a>-b
例4.如果 ,试比较 的大小.
解:因为
所以
因为 ,
所以 ,
所以 , ,
所以 .
0
a
b
-b
-a
比较表示数的字母的大小
易错点
1.有理数a,b在数轴上的对应点的位置如图所示,下列结论正确的是( )
A.a>b B.|a|<|b| C.a>-b D.-a>b
D
2.a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,-a,b,-b按照从小到大的顺序排列为( )
A.-b<-a<a<b B.-a<-b<a<b
C.-b<a<-a<b D.-b<b<-a<a
C
例5.下表是几种液体在标准大气压下的沸点,则沸点最高的液体是( )
A.液态氧 B.液态氢
C.液态氮 D.液态氦
解析:易知-268.9<-253<-196<-183,所以液态氧的沸点最高.
A
有理数大小比较的应用
重点
1.下表是某省四个景区某天6时的气温,其中气温最低的是( )
A.石膏山 B.五台山 C.芦芽山 D.绵山
C
2.某公司抽检盒装牛奶的容量,超过标准容量的部分记为正数,不足的部分记为负数.从容量的角度看,以下四盒牛奶容量最接近标准的是( )
A. B. C. D.
【分析】解:A.+0.8的绝对值是0.8;B.-1.2的绝对值是1.2;C.-0.5的绝对值是0.5;D.+1的绝对值是1.
因为0.5<0.8<1<1.2,所以C选项的绝对值最小.
C
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
