1.2.4 绝对值(第一课时) 课件(23张PPT)
文档属性
| 名称 | 1.2.4 绝对值(第一课时) 课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 11:19:34 | ||
图片预览








文档简介
(共23张PPT)
第1章 有理数
1.2.4 绝对值
第一单元
1.理解绝对值的概念及其几何意义,通过从数、形两个方面理解绝对值的意义,初步了解数形结合的思想方法;(数形结合思想)
2.会求一个数的绝对值,知道一个数的绝对值,会求这个数;
3.通过应用绝对值解决实际问题,培养学生的学习兴趣,提高学生对数学的好奇心和求知欲.
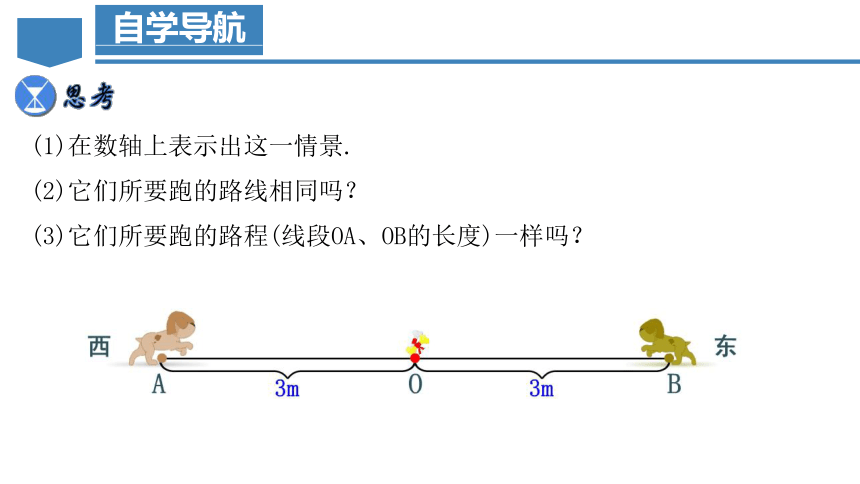
(1)在数轴上表示出这一情景.
(2)它们所要跑的路线相同吗?
(3)它们所要跑的路程(线段OA、OB的长度)一样吗?
(1)在数轴上表示出这一情景.
(2)它们所要跑的路线相同吗?
(3)它们所要跑的路程(线段OA、OB的长度)一样吗?
解:路线不同.
解:路程一样,到原点的距离相等(不管方向),OA=OB.
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,用“|a|”表示.
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
例1.求下列各数的绝对值:
-12,5,-,+,0,-5.8.
解:|-12|=12,|5|=5,|-|=,|+|=+,|0|=0,|-5.8|=5.8.
一个正数的绝对值是什么?一个负数的绝对值是什么?0的绝对值是什么?
求一个数的绝对值
重点
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0,那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
-a
0
|a|≥0
|-12|=12,|5|=5,|-|=,|+|=+,|0|=0,|-5.8|=5.8.
1.计算:
(1)=_____, =_____, -
(2)的绝对值等于______,的相反数等于______.
2.写出下列各数的绝对值:
-21,,-7.8,+3.
解:=21,=,=7.8,=3.
2
0.75
-
-
绝对值的意义理解
易错点
例2.下列说法正确的是( )
A.绝对值等于它本身的数是正数
B.绝对值等于它的相反数的数是负数
C.不存在绝对值最小的数
D.一个数的绝对值越小,表示它在数轴上对应的点离原点越近
绝对值的意义理解
易错点
1.数a,b,c在数轴上的对应点的位置如图所示,那么这三个数中绝对值最大的是( )
A.a B.b C.c D.无法确定
2.如果=a,那么有理数a一定是( )
A.正数 B.负数 C.非正数 D.非负数
A
D
3.如图,在数轴上每隔一个单位长度取一个点,若点A,B表示的数的绝对值相等,则点A表示的数是_______.
-2
|-5|=5
|+5|=5
相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
例3.对于任意有理数m,当m为何值时, 有最大值?最大值为多少?
【分析】根据绝对值的非负性得到 ,得到当m=3时, 最小,代入求解即可.
解:由绝对值都是非负数,得 .
当m=3时, 最小,最小值为0,此时有最大值,最大值是5.
绝对值的非负性
重点
1.当x=____时,5取最小值,这个最小值是_____;当a=____时,36-取最大值,这个最大值是_____.
2.已知=8,|a|>a,则a等于_____.
3.|x|=,则x=________; |-x|=______;若|-2.5|=|-a|,则a=_________.
0
5
2
36
2.5或-2.5
-8
或-
绝对值的非负性
重点
例4.若|x-4|+|y-6|=0,求x+y的值.
解:因为|x-4|≥0,|y-6|≥0,|x-4|+|y-6|=0,
所以x-4=0,y-6=0.
所以x=4,y=6.
所以x+y=4+6=10.
【解析】一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
1.若+=0,则|m+n|等于( )
A.2 B.7 C.8 D.9
【解析】由绝对值的非负性,得m-2=0,n-7=0,
所以m=2,n=7,
所以|m+n|=|2+7|=9.
故选 D.
2.若,求x+2y+3z的值.
解:由绝对值的非负性,得x-1=0,y-5=0,z-3=0,
所以x=1,y=5,z=3.
所以x+2y+3z=1+2×5+3×3=20.
绝对值几何意义的应用
难点
例5.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看最接近标准质量的是哪个足球 请用你所学的知识进行解释.
绝对值几何意义的应用
难点
例5.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看最接近标准质量的是哪个足球 请用你所学的知识进行解释.
解:因为=3.5,
=2.5,
=0.6,
=0.7,
0.6<0.7<2.5<3.5,
所以C足球最接近标准质量.
已知某零件的标准直径是100mm,超过标准直径的毫米数记作正数,不足标准直径的毫米数记作负数,检验员某次抽查了5件样品,记录如下:
(1)指出哪件样品的大小最符合要求;
(2)如果规定误差的绝对值在0.18mm以内的是正品,误差的绝对值在0.18~
0.22mm的是次品,误差的绝对值超过0.22mm的是废品,那么这5件样品分别属于哪类产品
解:(1)第4件样品的大小最符合要求.
(2)因为|+0.1|=0.1<0.18,|-0.15|=0.15<0.18,|-0.05|=0.05<0.18,
所以第1,2,4件样品是正品.
因为|+0.2|=0.2,0.18<0.2<0.22,
所以第3件样品为次品.
因为|+0.25|=0.25>0.22,
所以第5件样品为废品.
一般地,数轴上表示数 a 的点与原点的距离叫做数 a 的绝对值,记作|a|.
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0,那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
-a
0
|a|≥0
第1章 有理数
1.2.4 绝对值
第一单元
1.理解绝对值的概念及其几何意义,通过从数、形两个方面理解绝对值的意义,初步了解数形结合的思想方法;(数形结合思想)
2.会求一个数的绝对值,知道一个数的绝对值,会求这个数;
3.通过应用绝对值解决实际问题,培养学生的学习兴趣,提高学生对数学的好奇心和求知欲.
(1)在数轴上表示出这一情景.
(2)它们所要跑的路线相同吗?
(3)它们所要跑的路程(线段OA、OB的长度)一样吗?
(1)在数轴上表示出这一情景.
(2)它们所要跑的路线相同吗?
(3)它们所要跑的路程(线段OA、OB的长度)一样吗?
解:路线不同.
解:路程一样,到原点的距离相等(不管方向),OA=OB.
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,用“|a|”表示.
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
例1.求下列各数的绝对值:
-12,5,-,+,0,-5.8.
解:|-12|=12,|5|=5,|-|=,|+|=+,|0|=0,|-5.8|=5.8.
一个正数的绝对值是什么?一个负数的绝对值是什么?0的绝对值是什么?
求一个数的绝对值
重点
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0,那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
-a
0
|a|≥0
|-12|=12,|5|=5,|-|=,|+|=+,|0|=0,|-5.8|=5.8.
1.计算:
(1)=_____, =_____, -
(2)的绝对值等于______,的相反数等于______.
2.写出下列各数的绝对值:
-21,,-7.8,+3.
解:=21,=,=7.8,=3.
2
0.75
-
-
绝对值的意义理解
易错点
例2.下列说法正确的是( )
A.绝对值等于它本身的数是正数
B.绝对值等于它的相反数的数是负数
C.不存在绝对值最小的数
D.一个数的绝对值越小,表示它在数轴上对应的点离原点越近
绝对值的意义理解
易错点
1.数a,b,c在数轴上的对应点的位置如图所示,那么这三个数中绝对值最大的是( )
A.a B.b C.c D.无法确定
2.如果=a,那么有理数a一定是( )
A.正数 B.负数 C.非正数 D.非负数
A
D
3.如图,在数轴上每隔一个单位长度取一个点,若点A,B表示的数的绝对值相等,则点A表示的数是_______.
-2
|-5|=5
|+5|=5
相反数、绝对值的联系是什么?
互为相反数的两个数的绝对值相等.
绝对值相等,符号相反的两个数互为相反数.
例3.对于任意有理数m,当m为何值时, 有最大值?最大值为多少?
【分析】根据绝对值的非负性得到 ,得到当m=3时, 最小,代入求解即可.
解:由绝对值都是非负数,得 .
当m=3时, 最小,最小值为0,此时有最大值,最大值是5.
绝对值的非负性
重点
1.当x=____时,5取最小值,这个最小值是_____;当a=____时,36-取最大值,这个最大值是_____.
2.已知=8,|a|>a,则a等于_____.
3.|x|=,则x=________; |-x|=______;若|-2.5|=|-a|,则a=_________.
0
5
2
36
2.5或-2.5
-8
或-
绝对值的非负性
重点
例4.若|x-4|+|y-6|=0,求x+y的值.
解:因为|x-4|≥0,|y-6|≥0,|x-4|+|y-6|=0,
所以x-4=0,y-6=0.
所以x=4,y=6.
所以x+y=4+6=10.
【解析】一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
1.若+=0,则|m+n|等于( )
A.2 B.7 C.8 D.9
【解析】由绝对值的非负性,得m-2=0,n-7=0,
所以m=2,n=7,
所以|m+n|=|2+7|=9.
故选 D.
2.若,求x+2y+3z的值.
解:由绝对值的非负性,得x-1=0,y-5=0,z-3=0,
所以x=1,y=5,z=3.
所以x+2y+3z=1+2×5+3×3=20.
绝对值几何意义的应用
难点
例5.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看最接近标准质量的是哪个足球 请用你所学的知识进行解释.
绝对值几何意义的应用
难点
例5.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看最接近标准质量的是哪个足球 请用你所学的知识进行解释.
解:因为=3.5,
=2.5,
=0.6,
=0.7,
0.6<0.7<2.5<3.5,
所以C足球最接近标准质量.
已知某零件的标准直径是100mm,超过标准直径的毫米数记作正数,不足标准直径的毫米数记作负数,检验员某次抽查了5件样品,记录如下:
(1)指出哪件样品的大小最符合要求;
(2)如果规定误差的绝对值在0.18mm以内的是正品,误差的绝对值在0.18~
0.22mm的是次品,误差的绝对值超过0.22mm的是废品,那么这5件样品分别属于哪类产品
解:(1)第4件样品的大小最符合要求.
(2)因为|+0.1|=0.1<0.18,|-0.15|=0.15<0.18,|-0.05|=0.05<0.18,
所以第1,2,4件样品是正品.
因为|+0.2|=0.2,0.18<0.2<0.22,
所以第3件样品为次品.
因为|+0.25|=0.25>0.22,
所以第5件样品为废品.
一般地,数轴上表示数 a 的点与原点的距离叫做数 a 的绝对值,记作|a|.
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0,那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
-a
0
|a|≥0
