1.3探索三角形全等的条件(第2课时) 课件(27张PPT)
文档属性
| 名称 | 1.3探索三角形全等的条件(第2课时) 课件(27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 11:23:40 | ||
图片预览




文档简介
第1章 · 全等三角形
1.3 探索三角形全等的条件
第2课时 边角边的应用
学习目标
熟练运用“边角边”判定两个三角形全等,提高有条理地思考和说理能力.
问题情境
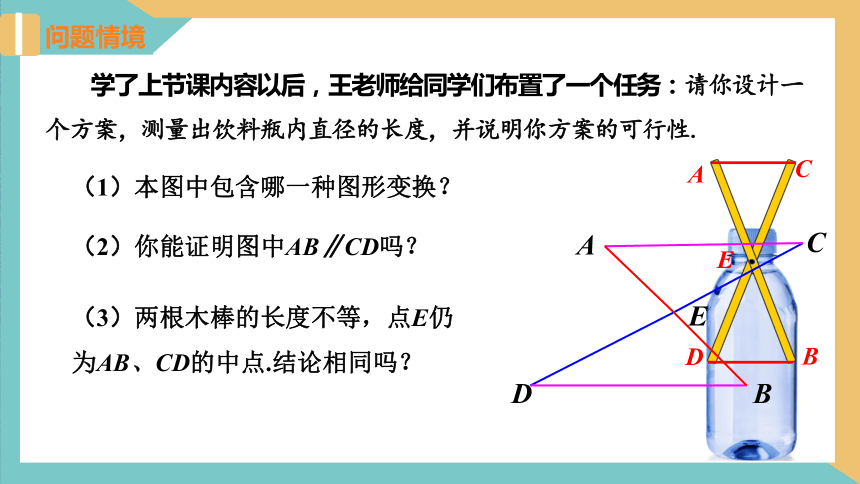
学了上节课内容以后,王老师给同学们布置了一个任务:请你设计一个方案,测量出饮料瓶内直径的长度,并说明你方案的可行性.
小明给出如下方案:
找两根长度相等的木棒,在中点处固定,按如图方法放置处于同一水平位置,测量出AC的长度即为塑料瓶内直径的长度.
D
B
A
C
E
你认为小明给出的方案合理吗?说出你的理由.
问题情境
学了上节课内容以后,王老师给同学们布置了一个任务:请你设计一个方案,测量出饮料瓶内直径的长度,并说明你方案的可行性.
我认为小明给出的方案合理. 理由如下:
∵E是AB、CD的中点(已知),
∴AE=BE,CE=DE (线段中点的定义).
在△AEC和△BED中,
????????=????????(已证),∠????????????=∠????????????(对顶角相等),?????????=????????(已证).
∴ △AEC≌ △BED(SAS).
∴AC=DB(全等三角形对应边相等).
∴测量AC的长度即为饮料瓶内直径的长度.
?
D
B
A
C
E
问题情境
学了上节课内容以后,王老师给同学们布置了一个任务:请你设计一个方案,测量出饮料瓶内直径的长度,并说明你方案的可行性.
(1)本图中包含哪一种图形变换?
(2)你能证明图中AB∥CD吗?
(3)两根木棒的长度不等,点E仍为AB、CD的中点.结论相同吗?
D
B
A
C
E
A
E
C
D
B
新知探索
A
E
C
D
B
F
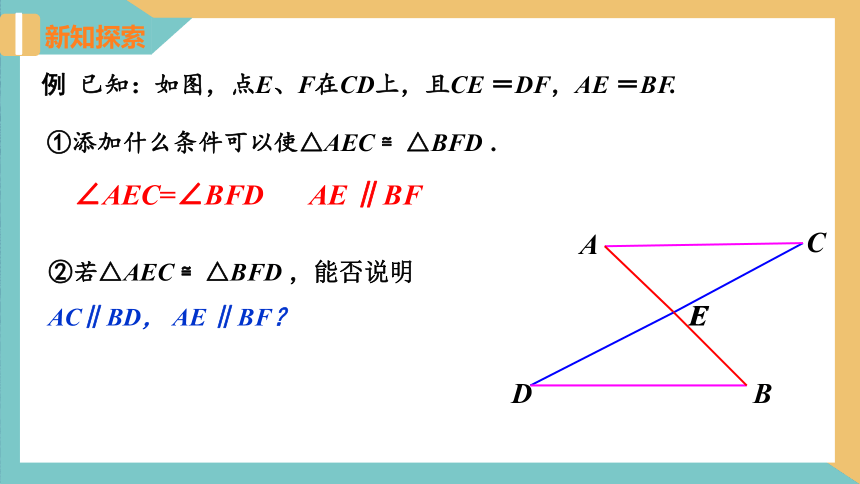
例 已知:如图,点E、F在CD上,且CE =DF,AE =BF.
①添加什么条件可以使△AEC ≌△BFD .
∠AEC=∠BFD
AE ∥BF
②若△AEC ≌△BFD ,能否说明AC∥BD, AE ∥BF?
新知探索
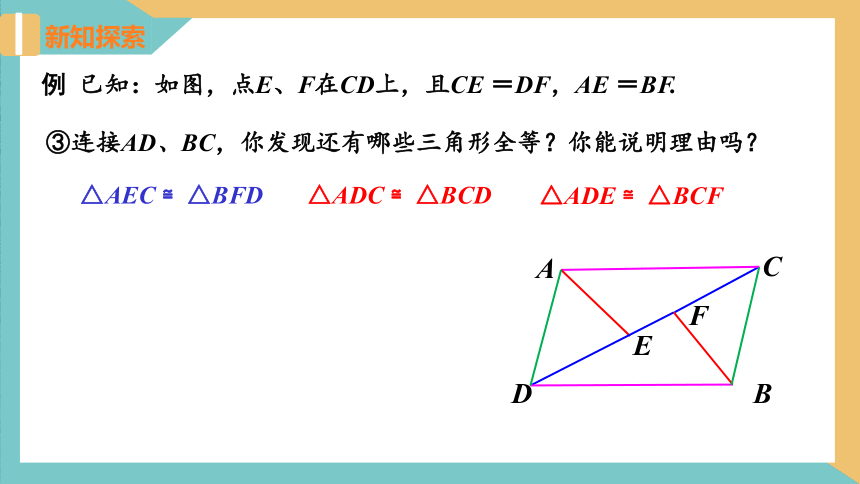
例 已知:如图,点E、F在CD上,且CE =DF,AE =BF.
A
E
C
D
B
F
△AEC ≌△BFD
△ADE ≌△BCF
△ADC ≌△BCD
③连接AD、BC,你发现还有哪些三角形全等?你能说明理由吗?
新知探索
A
E
C
D
B
F
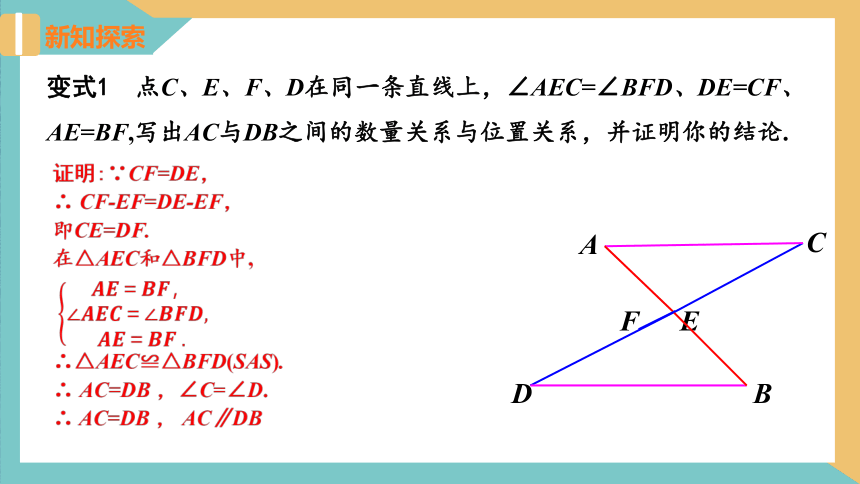
变式1 点C、E、F、D在同一条直线上,∠AEC=∠BFD、DE=CF、AE=BF,写出AC与DB之间的数量关系与位置关系,并证明你的结论.
证明:∵CF=DE,
∴ CF-EF=DE-EF,
即CE=DF.
在△AEC和△BFD中,
????????=????????,∠????????????=∠????????????,?????????=?????????.
∴△AEC≌△BFD(SAS).
∴ AC=DB ,∠C=∠D.
∴ AC=DB , AC∥DB
?
新知探索
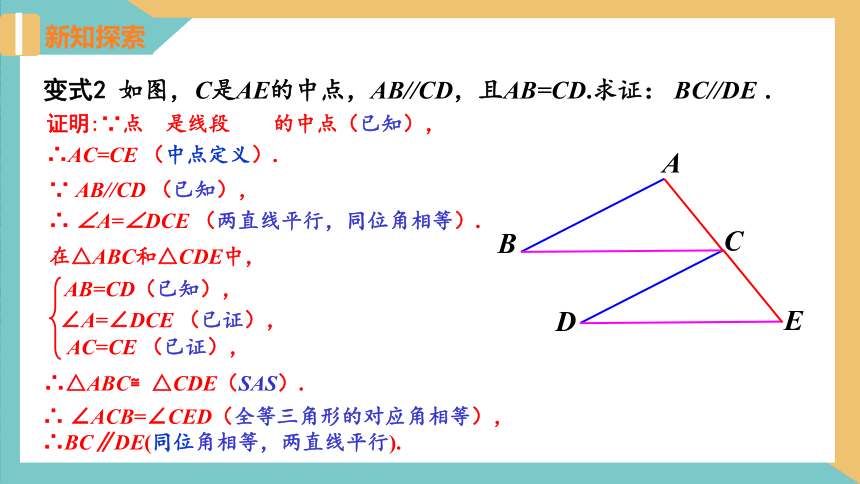
变式2 如图,C是AE的中点,AB//CD,且AB=CD.求证: BC//DE .
AC=CE (已证),
证明:∵点????是线段????????的中点(已知),
∴AC=CE (中点定义).
∵ AB//CD (已知),
∴ ∠A=∠DCE (两直线平行,同位角相等).
在△ABC和△CDE中,
∴△ABC≌△CDE(SAS).
AB=CD(已知),
∠A=∠DCE (已证),
D
E
C
B
A
∴ ∠ACB=∠CED(全等三角形的对应角相等),
∴BC∥DE(同位角相等,两直线平行).
新知探索
变式3 如图,点A、D、C、B在同一条直线上,AD=CB,AE=BF,AE∥BF.请探索CE与DF有怎样的位置关系?
AC=BD (已证),
证明:∵AE∥BF,
∴∠A=∠B(两直线平行,内错角相等).
∴ ∠ACE=∠BDF(全等三角形的对应角相等),
∴CE∥DF(内错角相等,两直线平行).
又∵ AD=CB,∴ AD+DC=CB+DC,即AC=BD.
在△AEC和△DFB中,
∴△AEC≌△DFB(SAS),
AE=BF(已知),
∠A=∠B (已证),
A
E
C
D
B
F
新知归纳
①准备条件:证全等时要用的间接条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
证明的书写步骤:
新知巩固
D
C
B
A
1.如图,△ABC中, AB =AC,AD平分∠BAC .
(1)求证:△ABD ≌ △ACD.
(2)求证:AD⊥BC
证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
????????=????????,∠????????????=∠?????????????,?????????=?????????.
∴△ABD≌△ACD(SAS).
?
本图中包含哪一种图形变换?
新知巩固
D
C
B
A
1.如图,△ABC中, AB =AC,AD平分∠BAC .
(1)求证:△ABD ≌ △ACD.
(2)求证:AD⊥BC
证明:(2)∵△ABD≌△ACD,∴∠ADB=∠ADC.
∵∠ADB+∠ADC=180°
∴∠ADB=∠ADC=90°
∴AD⊥BC
新知巩固
2. 如图,已知AB∥CD,AB=CD,求证: AB∥CD ,AD=BC.
D
A
C
B
2
1
本图中包含哪一种图形变换?
证明:∵AB∥CD (已知),
∴∠1=∠2 (两直线平行,内错角相等).
在△ABD和△CDB中,
????????=????????(已知),∠????=∠????(已证),?????????=????????(公共边).?
∴△ABD≌△CDB(SAS),
∴ AD=BC ,∠ADB=∠CBD (全等三角形对应边、对应角相等).
∴ AB∥CD ,AD=BC(内错角相等、两直线平行).
?
课堂小结
边角边
内容
应用
书写步骤
注意点
当堂检测
1.下列条件中,能作出唯一三角形的是( )
A.已知三个角
B.已知两边和其中一边的对角
C.已知三角形的周长
D.已知两边和它们的夹角
D
当堂检测
2.如图,OA=OB,OC=OD. 若∠D=35°,则∠C等于( )
A.60° B.50° C.35° D.条件不够,无法求出
C
O
A
B
C
D
当堂检测
3.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,有下列结论:
①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC.
其中正确的是( )
A.①② B.①②③ C.①③ D.②③
∟
∟
A
B
C
D
O
C
当堂检测
4.如图,AB=AD,∠BAD=∠CAE ,如果增加一个条件_________,那么就可以根据“SAS”证明△ABC≌△ADE.
A
E
D
C
B
AC=AE
1
当堂检测
5.如图,AD=AE,∠1=∠2,BD=CE,则△ABE≌_________,判定依据是__________.
A
C
D
B
E
2
△ACD
SAS
6.如图,AB=CD,要判定△ABC≌△CDA,还需要的一个条件是___________________.
A
D
B
C
当堂检测
∠BAC=∠DCA
当堂检测
7. 如图,线段AD,CE相交于点B,BC=BD,AB=EB,
求证:△ACD≌△EDC.
证明:∵BC=BD,
∴∠ADC=∠ECD.
∵AB=EB,
∴BC+EB=BD+AB,即CE=DA.
在△ACD和△EDC中,
????????=?????????,?∠????????????=∠????????????,?????????=????????.?
∴△ACD≌△EDC(SAS).
?
C
D
A
B
E
当堂检测
8.如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.
求证:AF=DE.
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
????????=?????????,?∠????=∠????,?????????=????????.?
∴△ABF≌△DCE(SAS).
∴AF=DE.
?
A
F
B
D
E
C
当堂检测
9.已知:如图,BE⊥CD于点E,BE=DE,AE=CE,DA的延长线交BC于点F.
求证:DF⊥BC.
∟
A
B
C
D
E
F
证明:∵BE⊥CD,
∴∠BEC=∠DEA=90°.
在△BEC和△DEA中,
????????=????????,???∠????????????=∠?????????????,?????????=?????????.???????
∴△BEC≌△DEA(SAS).
∴∠B=∠D.
又∵∠B+∠C=90°,
∴∠D+∠C=90°.
∴∠CFD=90°.
即DF⊥BC.
?
当堂检测
10. 如图,AD是△ABC的中线,在AD及其延长线上截取DE=DF,连接CE,BF,△BDF与△CDE全等吗?BF与CE有何位置关系?请说明理由.
D
C
B
A
F
E
解:△BDF与△CDE全等,BF∥CE.
理由如下:
∵AD是△ABC的中线,
∴BD=CD.
在△BDF和△CDE中,
????????=????????(已证),???????????????????∠????????????=∠????????????(对顶角相等),?????????=????????(已知).???????????????????????
∴△BDF≌△CDE(SAS),
∴∠F=∠DEC,
∴BF∥CE.
?
拓展延伸
“倍长中线法”是解决几何问题的重要方法.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,具体做法是:
如图,AD是△ABC的中线,延长AD 到E ,使DE=AD,连接BE ,构造出△BED和△CAD .求证:△BED≌△CAD.
A
B
C
D
E
证明:∵AD 是 △ABC 的中线,
∴DB=DC
在△BED和△CAD中,
????????=????????,???∠????????????=∠????????????,?????????=?????????.???????
∴△BED≌△CAD(SAS).
?
拓展延伸
若AB=5, AC=3,则BC边上的中线AD的取值范围是__________.
A
B
C
D
E
解:∵△BED≌△CAD,
∴AD=DE,BE=AC=3.
在△AEB中,
AB-BE<AE<AB+BE,
即5-3<2AD<5+3,
∴ 1<AD<4,
∴AD的取值范围是1<AD<4.
1.3 探索三角形全等的条件
第2课时 边角边的应用
学习目标
熟练运用“边角边”判定两个三角形全等,提高有条理地思考和说理能力.
问题情境
学了上节课内容以后,王老师给同学们布置了一个任务:请你设计一个方案,测量出饮料瓶内直径的长度,并说明你方案的可行性.
小明给出如下方案:
找两根长度相等的木棒,在中点处固定,按如图方法放置处于同一水平位置,测量出AC的长度即为塑料瓶内直径的长度.
D
B
A
C
E
你认为小明给出的方案合理吗?说出你的理由.
问题情境
学了上节课内容以后,王老师给同学们布置了一个任务:请你设计一个方案,测量出饮料瓶内直径的长度,并说明你方案的可行性.
我认为小明给出的方案合理. 理由如下:
∵E是AB、CD的中点(已知),
∴AE=BE,CE=DE (线段中点的定义).
在△AEC和△BED中,
????????=????????(已证),∠????????????=∠????????????(对顶角相等),?????????=????????(已证).
∴ △AEC≌ △BED(SAS).
∴AC=DB(全等三角形对应边相等).
∴测量AC的长度即为饮料瓶内直径的长度.
?
D
B
A
C
E
问题情境
学了上节课内容以后,王老师给同学们布置了一个任务:请你设计一个方案,测量出饮料瓶内直径的长度,并说明你方案的可行性.
(1)本图中包含哪一种图形变换?
(2)你能证明图中AB∥CD吗?
(3)两根木棒的长度不等,点E仍为AB、CD的中点.结论相同吗?
D
B
A
C
E
A
E
C
D
B
新知探索
A
E
C
D
B
F
例 已知:如图,点E、F在CD上,且CE =DF,AE =BF.
①添加什么条件可以使△AEC ≌△BFD .
∠AEC=∠BFD
AE ∥BF
②若△AEC ≌△BFD ,能否说明AC∥BD, AE ∥BF?
新知探索
例 已知:如图,点E、F在CD上,且CE =DF,AE =BF.
A
E
C
D
B
F
△AEC ≌△BFD
△ADE ≌△BCF
△ADC ≌△BCD
③连接AD、BC,你发现还有哪些三角形全等?你能说明理由吗?
新知探索
A
E
C
D
B
F
变式1 点C、E、F、D在同一条直线上,∠AEC=∠BFD、DE=CF、AE=BF,写出AC与DB之间的数量关系与位置关系,并证明你的结论.
证明:∵CF=DE,
∴ CF-EF=DE-EF,
即CE=DF.
在△AEC和△BFD中,
????????=????????,∠????????????=∠????????????,?????????=?????????.
∴△AEC≌△BFD(SAS).
∴ AC=DB ,∠C=∠D.
∴ AC=DB , AC∥DB
?
新知探索
变式2 如图,C是AE的中点,AB//CD,且AB=CD.求证: BC//DE .
AC=CE (已证),
证明:∵点????是线段????????的中点(已知),
∴AC=CE (中点定义).
∵ AB//CD (已知),
∴ ∠A=∠DCE (两直线平行,同位角相等).
在△ABC和△CDE中,
∴△ABC≌△CDE(SAS).
AB=CD(已知),
∠A=∠DCE (已证),
D
E
C
B
A
∴ ∠ACB=∠CED(全等三角形的对应角相等),
∴BC∥DE(同位角相等,两直线平行).
新知探索
变式3 如图,点A、D、C、B在同一条直线上,AD=CB,AE=BF,AE∥BF.请探索CE与DF有怎样的位置关系?
AC=BD (已证),
证明:∵AE∥BF,
∴∠A=∠B(两直线平行,内错角相等).
∴ ∠ACE=∠BDF(全等三角形的对应角相等),
∴CE∥DF(内错角相等,两直线平行).
又∵ AD=CB,∴ AD+DC=CB+DC,即AC=BD.
在△AEC和△DFB中,
∴△AEC≌△DFB(SAS),
AE=BF(已知),
∠A=∠B (已证),
A
E
C
D
B
F
新知归纳
①准备条件:证全等时要用的间接条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
证明的书写步骤:
新知巩固
D
C
B
A
1.如图,△ABC中, AB =AC,AD平分∠BAC .
(1)求证:△ABD ≌ △ACD.
(2)求证:AD⊥BC
证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
????????=????????,∠????????????=∠?????????????,?????????=?????????.
∴△ABD≌△ACD(SAS).
?
本图中包含哪一种图形变换?
新知巩固
D
C
B
A
1.如图,△ABC中, AB =AC,AD平分∠BAC .
(1)求证:△ABD ≌ △ACD.
(2)求证:AD⊥BC
证明:(2)∵△ABD≌△ACD,∴∠ADB=∠ADC.
∵∠ADB+∠ADC=180°
∴∠ADB=∠ADC=90°
∴AD⊥BC
新知巩固
2. 如图,已知AB∥CD,AB=CD,求证: AB∥CD ,AD=BC.
D
A
C
B
2
1
本图中包含哪一种图形变换?
证明:∵AB∥CD (已知),
∴∠1=∠2 (两直线平行,内错角相等).
在△ABD和△CDB中,
????????=????????(已知),∠????=∠????(已证),?????????=????????(公共边).?
∴△ABD≌△CDB(SAS),
∴ AD=BC ,∠ADB=∠CBD (全等三角形对应边、对应角相等).
∴ AB∥CD ,AD=BC(内错角相等、两直线平行).
?
课堂小结
边角边
内容
应用
书写步骤
注意点
当堂检测
1.下列条件中,能作出唯一三角形的是( )
A.已知三个角
B.已知两边和其中一边的对角
C.已知三角形的周长
D.已知两边和它们的夹角
D
当堂检测
2.如图,OA=OB,OC=OD. 若∠D=35°,则∠C等于( )
A.60° B.50° C.35° D.条件不够,无法求出
C
O
A
B
C
D
当堂检测
3.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,有下列结论:
①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC.
其中正确的是( )
A.①② B.①②③ C.①③ D.②③
∟
∟
A
B
C
D
O
C
当堂检测
4.如图,AB=AD,∠BAD=∠CAE ,如果增加一个条件_________,那么就可以根据“SAS”证明△ABC≌△ADE.
A
E
D
C
B
AC=AE
1
当堂检测
5.如图,AD=AE,∠1=∠2,BD=CE,则△ABE≌_________,判定依据是__________.
A
C
D
B
E
2
△ACD
SAS
6.如图,AB=CD,要判定△ABC≌△CDA,还需要的一个条件是___________________.
A
D
B
C
当堂检测
∠BAC=∠DCA
当堂检测
7. 如图,线段AD,CE相交于点B,BC=BD,AB=EB,
求证:△ACD≌△EDC.
证明:∵BC=BD,
∴∠ADC=∠ECD.
∵AB=EB,
∴BC+EB=BD+AB,即CE=DA.
在△ACD和△EDC中,
????????=?????????,?∠????????????=∠????????????,?????????=????????.?
∴△ACD≌△EDC(SAS).
?
C
D
A
B
E
当堂检测
8.如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.
求证:AF=DE.
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
????????=?????????,?∠????=∠????,?????????=????????.?
∴△ABF≌△DCE(SAS).
∴AF=DE.
?
A
F
B
D
E
C
当堂检测
9.已知:如图,BE⊥CD于点E,BE=DE,AE=CE,DA的延长线交BC于点F.
求证:DF⊥BC.
∟
A
B
C
D
E
F
证明:∵BE⊥CD,
∴∠BEC=∠DEA=90°.
在△BEC和△DEA中,
????????=????????,???∠????????????=∠?????????????,?????????=?????????.???????
∴△BEC≌△DEA(SAS).
∴∠B=∠D.
又∵∠B+∠C=90°,
∴∠D+∠C=90°.
∴∠CFD=90°.
即DF⊥BC.
?
当堂检测
10. 如图,AD是△ABC的中线,在AD及其延长线上截取DE=DF,连接CE,BF,△BDF与△CDE全等吗?BF与CE有何位置关系?请说明理由.
D
C
B
A
F
E
解:△BDF与△CDE全等,BF∥CE.
理由如下:
∵AD是△ABC的中线,
∴BD=CD.
在△BDF和△CDE中,
????????=????????(已证),???????????????????∠????????????=∠????????????(对顶角相等),?????????=????????(已知).???????????????????????
∴△BDF≌△CDE(SAS),
∴∠F=∠DEC,
∴BF∥CE.
?
拓展延伸
“倍长中线法”是解决几何问题的重要方法.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,具体做法是:
如图,AD是△ABC的中线,延长AD 到E ,使DE=AD,连接BE ,构造出△BED和△CAD .求证:△BED≌△CAD.
A
B
C
D
E
证明:∵AD 是 △ABC 的中线,
∴DB=DC
在△BED和△CAD中,
????????=????????,???∠????????????=∠????????????,?????????=?????????.???????
∴△BED≌△CAD(SAS).
?
拓展延伸
若AB=5, AC=3,则BC边上的中线AD的取值范围是__________.
A
B
C
D
E
解:∵△BED≌△CAD,
∴AD=DE,BE=AC=3.
在△AEB中,
AB-BE<AE<AB+BE,
即5-3<2AD<5+3,
∴ 1<AD<4,
∴AD的取值范围是1<AD<4.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
