第二十八章 锐角三角函数(二) 人教版数学九年级下册(含解析)
文档属性
| 名称 | 第二十八章 锐角三角函数(二) 人教版数学九年级下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 333.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 18:35:51 | ||
图片预览


文档简介
《第二十八章 锐角三角函数》专项拓展训练(二)
专项一 构造基本图形解直角三角形的实际应用
类型1 构造单一直角三角形
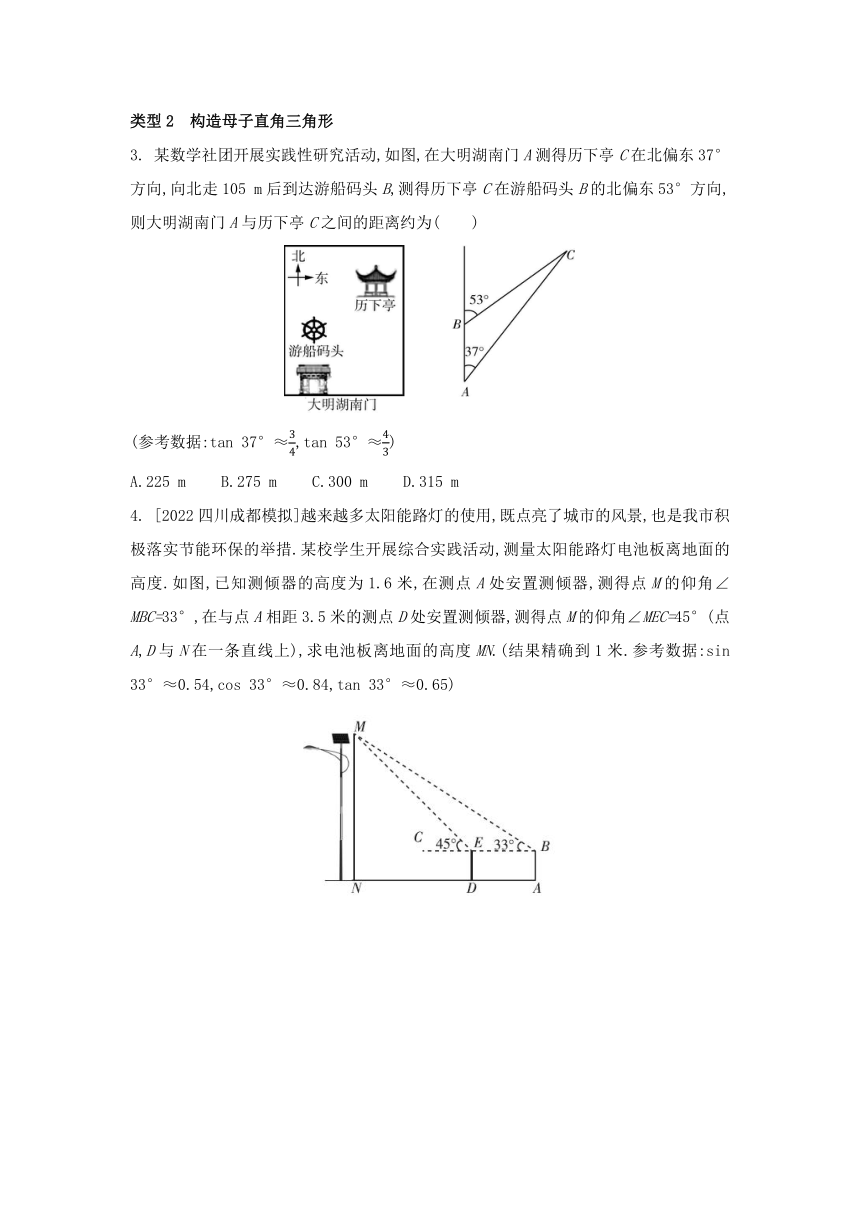
1. 如图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC是可伸缩的,其转动点A距离地面BD的高度AE为3.5 m.当AC长度为9 m,张角∠CAE为112°时,求云梯消防车最高点C距离地面的高度CF.(结果精确到0.1 m.参考数据:sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40)
2. [2022湖南长沙雨花区模拟]某地下车库入口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起到如图2所示的位置,图3是其示意图(不计栏杆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.3 m,请问一辆2.3 m高的小货车能否从此进入地下车库 并说明理由.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
类型2 构造母子直角三角形
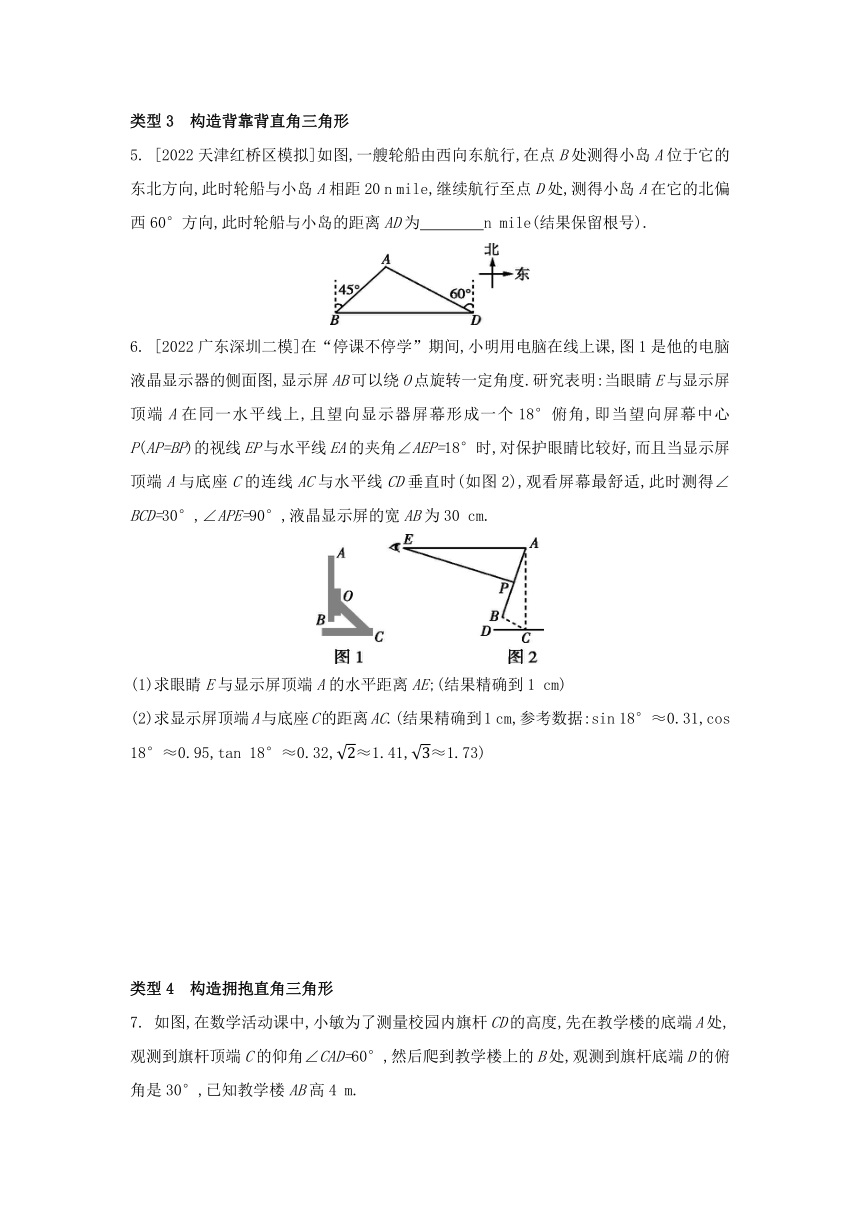
3. 某数学社团开展实践性研究活动,如图,在大明湖南门A测得历下亭C在北偏东37°方向,向北走105 m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向,则大明湖南门A与历下亭C之间的距离约为( )
(参考数据:tan 37°≈,tan 53°≈)
A.225 m B.275 m C.300 m D.315 m
4. [2022四川成都模拟]越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角∠MBC=33°,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角∠MEC=45°(点A,D与N在一条直线上),求电池板离地面的高度MN.(结果精确到1米.参考数据:sin 33°≈0.54,cos 33°≈0.84,tan 33°≈0.65)
类型3 构造背靠背直角三角形
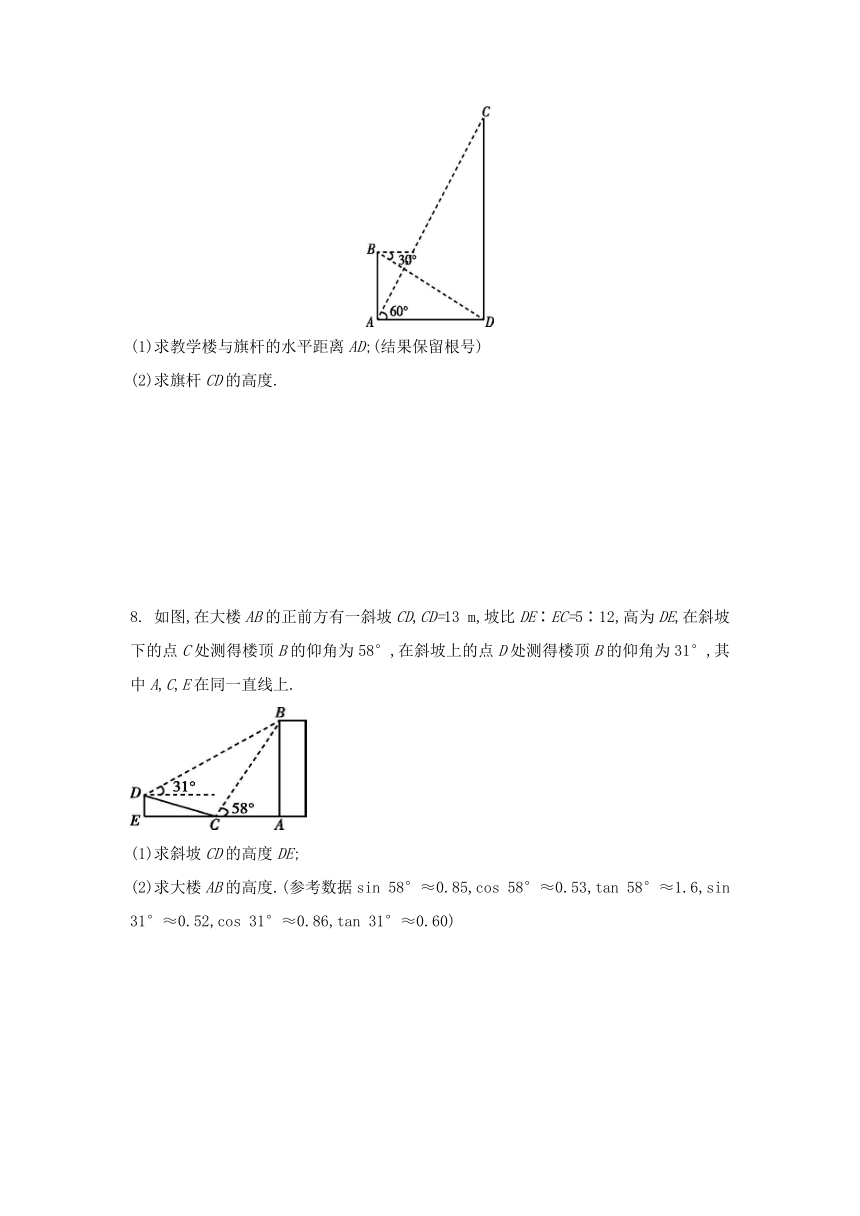
5. [2022天津红桥区模拟]如图,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛A相距20 n mile,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为 n mile(结果保留根号).
6. [2022广东深圳二模]在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角,即当望向屏幕中心P(AP=BP)的视线EP与水平线EA的夹角∠AEP=18°时,对保护眼睛比较好,而且当显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2),观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为30 cm.
(1)求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1 cm)
(2)求显示屏顶端A与底座C的距离AC.(结果精确到1 cm,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32,≈1.41,≈1.73)
类型4 构造拥抱直角三角形
7. 如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4 m.
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
8. 如图,在大楼AB的正前方有一斜坡CD,CD=13 m,坡比DE∶EC=5∶12,高为DE,在斜坡下的点C处测得楼顶B的仰角为58°,在斜坡上的点D处测得楼顶B的仰角为31°,其中A,C,E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度.(参考数据sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.6,sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
专项二 解直角三角形
1. [2022河北唐山路南区二模]如图,某停车场入口的栏杆AB,从水平位置绕点O顺时针旋转到A'B'的位置,已知AO的长为4米.若栏杆的旋转角∠AOA'=α,则栏杆A端升高的高度为 ( )
A. 米 B. 米
C.4sin α米 D.4cos α米
2. [2022河北邢台金华中学期中]在正方形网格中,小正方形的边长均为1,∠ABC如图放置,则sin∠ABC的值为 ( )
A. B. C. D.1
3. [2022河北石家庄外国语学校段考]如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是 ( )
A. B. C. D.
4. [2022河北张家口模拟]如图,在Rt△ABC中,∠C=90°,BC=8,tan B=,点D在BC上,且BD=AD,则cos∠ADC的值为 .
5. [2022河北承德模拟]如图,△ABC中,∠ACB=90°,sin A=,BC=8,D是AB的中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
参考答案
专项一 构造基本图形解直角三角形的实际应用
1.【解析】 如图,过点A作AG⊥CF于点G.
∵∠AEF=∠EFG=∠FGA=90°,
∴四边形AEFG为矩形,
∴FG=AE=3.5 m,∠EAG=90°,
∵∠EAC=112°,∴∠GAC=∠EAC-∠EAG=112°-90°=22°.
在Rt△ACG中,sin∠CAG=,
∴CG=ACsin∠CAG=9×sin 22°≈9×0.37=3.33(m),
∴CF=CG+GF≈3.33+3.5≈6.8(m).
答:云梯消防车最高点C距离地面的高度CF约为6.8 m.
2.【解析】 不能.理由如下:
如图,过点A作AG∥BC,过点E作EH⊥AG于点H,
则∠EHG=90°.
∵EF∥BC,AG∥BC,∴EF∥AG.
∵∠AEF=143°,∴∠EAH=180°-143°=37°.
在Rt△EAH中,∠EHA=90°,∠EAH=37°,AE=1.3 m,
∴EH=AEsin∠EAH≈0.78 m.
∵AB=1.3 m,∴AB+EH≈2.08 m<2.3 m.
∴小货车不能从此进入地下车库.
3.C 【解析】 如图,过点C作CE⊥AB于点E.设EC=x m,BE=y m.在Rt△ECB中,tan 53°==,在Rt△AEC中,tan 37°==,∴x≈180,y≈135,∴AC=≈
=300(m).
4.【解析】 如图,延长BC交MN于点H,则∠MHB=90°.
易得四边形BHNA和四边形ABED都是矩形,
∴NH=AB=1.6,BE=AD=3.5.
设MH=x.∵∠MEH=45°,
∴EH=MH=x,∴BH=x+3.5.
在Rt△MHB中,∵tan∠MBH=,∠MBH=33°,
∴≈0.65, ∴x≈6.5,
∴MN=MH+NH≈6.5+1.6=8.1≈8.
答:电池板离地面的高度MN约为8米.
5.20 【解析】 如图,过点A作AC⊥BD于点C,则∠ACB=∠ACD=90°.由题意得∠BAC=45°,∠DAC=60°,AB=20 n mile.在Rt△ABC中,AC=ABcos 45°=10 n mile,
∴AD==20 n mile.
6.【解析】 (1)由题意得AP=BP=AB=15 cm.
在Rt△APE中,∵sin∠AEP=,
∴AE==≈48(cm).
答:眼睛E与显示屏顶端A的水平距离AE约为48 cm.
(2)如图,过点B作BF⊥AC于点F,
∵∠EAB+∠BAF=90°,∠EAB+∠AEP=90°,
∴∠BAF=∠AEP=18°.
在Rt△ABF中,AF=ABcos∠BAF=30×cos 18°≈28.5(cm),
BF=ABsin∠BAF=30×sin 18°≈9.3(cm).
∵BF∥CD,∴∠CBF=∠BCD=30°,
∴CF=BFtan∠CBF≈9.3×tan 30°≈5.36(cm),
∴AC=AF+CF≈28.5+5.36≈34(cm).
答:显示屏顶端A与底座C的距离AC约为34 cm.
7.【解析】 (1)由题意可得∠ADB=30°,
在Rt△ABD中,∠BAD=90°,∠ADB=30°,AB=4 m,
∴AD===4(m).
答:教学楼与旗杆的水平距离AD是4 m.
(2)在Rt△ACD中,∠ADC=90°,∠CAD=60°,AD=4 m,
∴CD=ADtan 60°=4=12(m).
答:旗杆CD的高度是12 m.
8.【解析】 (1)∵DE∶EC=5∶12,∴设DE=5x m,EC=12x m,
∵CD=13 m,∴(5x)2+(12x)2=132,
∴x=1,∴DE=5 m,EC=12 m.
答:斜坡CD的高度DE是5 m.
(2)如图,过点D作DF⊥AB于点F,
在Rt△ABC中,tan 58°=,在Rt△BDF中,tan 31°==,
由(1)知DE=5 m,CE=12 m,
∴≈1.6,≈0.6,∴AB≈19.52 m.
答:大楼AB的高度约是19.52 m.
专项二 解直角三角形
1.C 【解析】 如图,过点A'作A'C⊥AB于点C→sin α= A'C=4sin α 米.
2.B 【解析】 如图,过点A作AD⊥BC于点D.由勾股定理,得BC==,
AB==,∵△ABC的面积=BC×AD=×2×1=1,∴××AD=1,解得AD=,∴sin∠ABC===.
3.A 【解析】 ∵四边形ABCD是矩形,点E是边BC的中点,∴BE=BC=AD,AD∥BC,∴△BEF∽△DAF,∴==,∴EF=AF,∴EF=AE.∵点E是边BC的中点,由矩形的对称性得AE=DE,∴EF=DE.设EF=x,则DE=3x.在Rt△DEF中,DF==2x,∴tan∠BDE===.
4. 【解析】 在Rt△ABC中,BC=8,tan B==,∴AC=4.设AD=x,则BD=x,所以CD=8-x.在Rt△ADC中,由勾股定理得,(8-x)2+42=x2,解得x=5,∴AD=5,CD=8-5=3,∴cos∠ADC==.
5.【解析】 (1)在△ABC中,∠ACB=90°,sin A==,BC=8,
∴AB=10.
∵D是AB的中点,∴CD=AB=5.
(2)在Rt△ABC中,AB=10,BC=8,
∴AC==6.
∵D是AB的中点,
∴BD=5,S△BDC=S△ADC,
∴S△BDC=S△ABC,即CD×BE=×AC×BC,
∴BE==,
在Rt△BDE中,cos∠DBE===,
即cos∠ABE的值为.
专项一 构造基本图形解直角三角形的实际应用
类型1 构造单一直角三角形
1. 如图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC是可伸缩的,其转动点A距离地面BD的高度AE为3.5 m.当AC长度为9 m,张角∠CAE为112°时,求云梯消防车最高点C距离地面的高度CF.(结果精确到0.1 m.参考数据:sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40)
2. [2022湖南长沙雨花区模拟]某地下车库入口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起到如图2所示的位置,图3是其示意图(不计栏杆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.3 m,请问一辆2.3 m高的小货车能否从此进入地下车库 并说明理由.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
类型2 构造母子直角三角形
3. 某数学社团开展实践性研究活动,如图,在大明湖南门A测得历下亭C在北偏东37°方向,向北走105 m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向,则大明湖南门A与历下亭C之间的距离约为( )
(参考数据:tan 37°≈,tan 53°≈)
A.225 m B.275 m C.300 m D.315 m
4. [2022四川成都模拟]越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角∠MBC=33°,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角∠MEC=45°(点A,D与N在一条直线上),求电池板离地面的高度MN.(结果精确到1米.参考数据:sin 33°≈0.54,cos 33°≈0.84,tan 33°≈0.65)
类型3 构造背靠背直角三角形
5. [2022天津红桥区模拟]如图,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛A相距20 n mile,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为 n mile(结果保留根号).
6. [2022广东深圳二模]在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角,即当望向屏幕中心P(AP=BP)的视线EP与水平线EA的夹角∠AEP=18°时,对保护眼睛比较好,而且当显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2),观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为30 cm.
(1)求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1 cm)
(2)求显示屏顶端A与底座C的距离AC.(结果精确到1 cm,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32,≈1.41,≈1.73)
类型4 构造拥抱直角三角形
7. 如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4 m.
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
8. 如图,在大楼AB的正前方有一斜坡CD,CD=13 m,坡比DE∶EC=5∶12,高为DE,在斜坡下的点C处测得楼顶B的仰角为58°,在斜坡上的点D处测得楼顶B的仰角为31°,其中A,C,E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度.(参考数据sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.6,sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
专项二 解直角三角形
1. [2022河北唐山路南区二模]如图,某停车场入口的栏杆AB,从水平位置绕点O顺时针旋转到A'B'的位置,已知AO的长为4米.若栏杆的旋转角∠AOA'=α,则栏杆A端升高的高度为 ( )
A. 米 B. 米
C.4sin α米 D.4cos α米
2. [2022河北邢台金华中学期中]在正方形网格中,小正方形的边长均为1,∠ABC如图放置,则sin∠ABC的值为 ( )
A. B. C. D.1
3. [2022河北石家庄外国语学校段考]如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是 ( )
A. B. C. D.
4. [2022河北张家口模拟]如图,在Rt△ABC中,∠C=90°,BC=8,tan B=,点D在BC上,且BD=AD,则cos∠ADC的值为 .
5. [2022河北承德模拟]如图,△ABC中,∠ACB=90°,sin A=,BC=8,D是AB的中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
参考答案
专项一 构造基本图形解直角三角形的实际应用
1.【解析】 如图,过点A作AG⊥CF于点G.
∵∠AEF=∠EFG=∠FGA=90°,
∴四边形AEFG为矩形,
∴FG=AE=3.5 m,∠EAG=90°,
∵∠EAC=112°,∴∠GAC=∠EAC-∠EAG=112°-90°=22°.
在Rt△ACG中,sin∠CAG=,
∴CG=ACsin∠CAG=9×sin 22°≈9×0.37=3.33(m),
∴CF=CG+GF≈3.33+3.5≈6.8(m).
答:云梯消防车最高点C距离地面的高度CF约为6.8 m.
2.【解析】 不能.理由如下:
如图,过点A作AG∥BC,过点E作EH⊥AG于点H,
则∠EHG=90°.
∵EF∥BC,AG∥BC,∴EF∥AG.
∵∠AEF=143°,∴∠EAH=180°-143°=37°.
在Rt△EAH中,∠EHA=90°,∠EAH=37°,AE=1.3 m,
∴EH=AEsin∠EAH≈0.78 m.
∵AB=1.3 m,∴AB+EH≈2.08 m<2.3 m.
∴小货车不能从此进入地下车库.
3.C 【解析】 如图,过点C作CE⊥AB于点E.设EC=x m,BE=y m.在Rt△ECB中,tan 53°==,在Rt△AEC中,tan 37°==,∴x≈180,y≈135,∴AC=≈
=300(m).
4.【解析】 如图,延长BC交MN于点H,则∠MHB=90°.
易得四边形BHNA和四边形ABED都是矩形,
∴NH=AB=1.6,BE=AD=3.5.
设MH=x.∵∠MEH=45°,
∴EH=MH=x,∴BH=x+3.5.
在Rt△MHB中,∵tan∠MBH=,∠MBH=33°,
∴≈0.65, ∴x≈6.5,
∴MN=MH+NH≈6.5+1.6=8.1≈8.
答:电池板离地面的高度MN约为8米.
5.20 【解析】 如图,过点A作AC⊥BD于点C,则∠ACB=∠ACD=90°.由题意得∠BAC=45°,∠DAC=60°,AB=20 n mile.在Rt△ABC中,AC=ABcos 45°=10 n mile,
∴AD==20 n mile.
6.【解析】 (1)由题意得AP=BP=AB=15 cm.
在Rt△APE中,∵sin∠AEP=,
∴AE==≈48(cm).
答:眼睛E与显示屏顶端A的水平距离AE约为48 cm.
(2)如图,过点B作BF⊥AC于点F,
∵∠EAB+∠BAF=90°,∠EAB+∠AEP=90°,
∴∠BAF=∠AEP=18°.
在Rt△ABF中,AF=ABcos∠BAF=30×cos 18°≈28.5(cm),
BF=ABsin∠BAF=30×sin 18°≈9.3(cm).
∵BF∥CD,∴∠CBF=∠BCD=30°,
∴CF=BFtan∠CBF≈9.3×tan 30°≈5.36(cm),
∴AC=AF+CF≈28.5+5.36≈34(cm).
答:显示屏顶端A与底座C的距离AC约为34 cm.
7.【解析】 (1)由题意可得∠ADB=30°,
在Rt△ABD中,∠BAD=90°,∠ADB=30°,AB=4 m,
∴AD===4(m).
答:教学楼与旗杆的水平距离AD是4 m.
(2)在Rt△ACD中,∠ADC=90°,∠CAD=60°,AD=4 m,
∴CD=ADtan 60°=4=12(m).
答:旗杆CD的高度是12 m.
8.【解析】 (1)∵DE∶EC=5∶12,∴设DE=5x m,EC=12x m,
∵CD=13 m,∴(5x)2+(12x)2=132,
∴x=1,∴DE=5 m,EC=12 m.
答:斜坡CD的高度DE是5 m.
(2)如图,过点D作DF⊥AB于点F,
在Rt△ABC中,tan 58°=,在Rt△BDF中,tan 31°==,
由(1)知DE=5 m,CE=12 m,
∴≈1.6,≈0.6,∴AB≈19.52 m.
答:大楼AB的高度约是19.52 m.
专项二 解直角三角形
1.C 【解析】 如图,过点A'作A'C⊥AB于点C→sin α= A'C=4sin α 米.
2.B 【解析】 如图,过点A作AD⊥BC于点D.由勾股定理,得BC==,
AB==,∵△ABC的面积=BC×AD=×2×1=1,∴××AD=1,解得AD=,∴sin∠ABC===.
3.A 【解析】 ∵四边形ABCD是矩形,点E是边BC的中点,∴BE=BC=AD,AD∥BC,∴△BEF∽△DAF,∴==,∴EF=AF,∴EF=AE.∵点E是边BC的中点,由矩形的对称性得AE=DE,∴EF=DE.设EF=x,则DE=3x.在Rt△DEF中,DF==2x,∴tan∠BDE===.
4. 【解析】 在Rt△ABC中,BC=8,tan B==,∴AC=4.设AD=x,则BD=x,所以CD=8-x.在Rt△ADC中,由勾股定理得,(8-x)2+42=x2,解得x=5,∴AD=5,CD=8-5=3,∴cos∠ADC==.
5.【解析】 (1)在△ABC中,∠ACB=90°,sin A==,BC=8,
∴AB=10.
∵D是AB的中点,∴CD=AB=5.
(2)在Rt△ABC中,AB=10,BC=8,
∴AC==6.
∵D是AB的中点,
∴BD=5,S△BDC=S△ADC,
∴S△BDC=S△ABC,即CD×BE=×AC×BC,
∴BE==,
在Rt△BDE中,cos∠DBE===,
即cos∠ABE的值为.
