4.4探究三角形相似的条件同步练习北师大版九年级数学上册(含解析)
文档属性
| 名称 | 4.4探究三角形相似的条件同步练习北师大版九年级数学上册(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 451.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 00:00:00 | ||
图片预览



文档简介
北师大版九上4.4探究三角形相似的条件
(共17题)
一、选择题(共10题)
如图,四边形 的对角线 , 相交于 ,且将这个四边形分成①,②,③,④四个三角形.若 ,则下列结论中一定正确的是
A.①和②相似 B.①和③相似 C.①和④相似 D.②和④相似
已知 如图所示,则下列 个三角形中,与 相似的是
A. B.
C. D.
若 是 的斜边 上异于 , 的一点,过点 作直线截 ,截得的三角形与原 相似,满足这样条件的直线共有
A. 条 B. 条 C. 条 D. 条
两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图, 是线段 上一点(),若满足 ,则称 是 的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长 米,主持人从舞台一侧进入,设他至少走 米时恰好站在舞台的黄金分割点上,则 满足的方程是
A. B.
C. D.以上都不对
如图,在 中,,,点 在 上,且 ,若要在 上找一点 ,使 与 相似,则 的长为
A. B. C. 或 D. 或
如图所示,在 中,, 于点 ,下列结论中错误的是
A. B.
C. D.
下列命题是真命题的为
A.同旁内角相等,两直线平行 B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形 D.两角分别相等的两个三角形相似
如图,在矩形 中,, 分别交 , 于点 ,, 分别交 , 于点 ,,若 ,,,则 的值为
A. B. C. D.
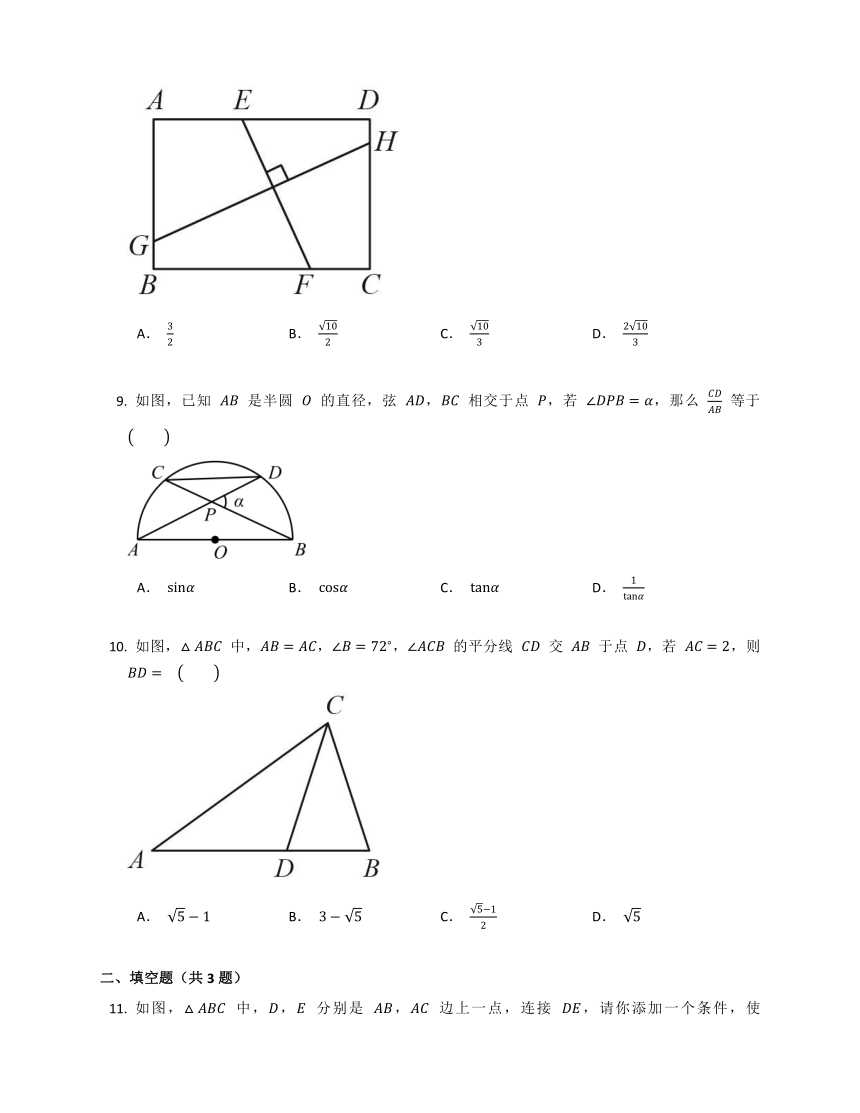
如图,已知 是半圆 的直径,弦 , 相交于点 ,若 ,那么 等于
A. B. C. D.
如图, 中,,, 的平分线 交 于点 ,若 ,则
A. B. C. D.
二、填空题(共3题)
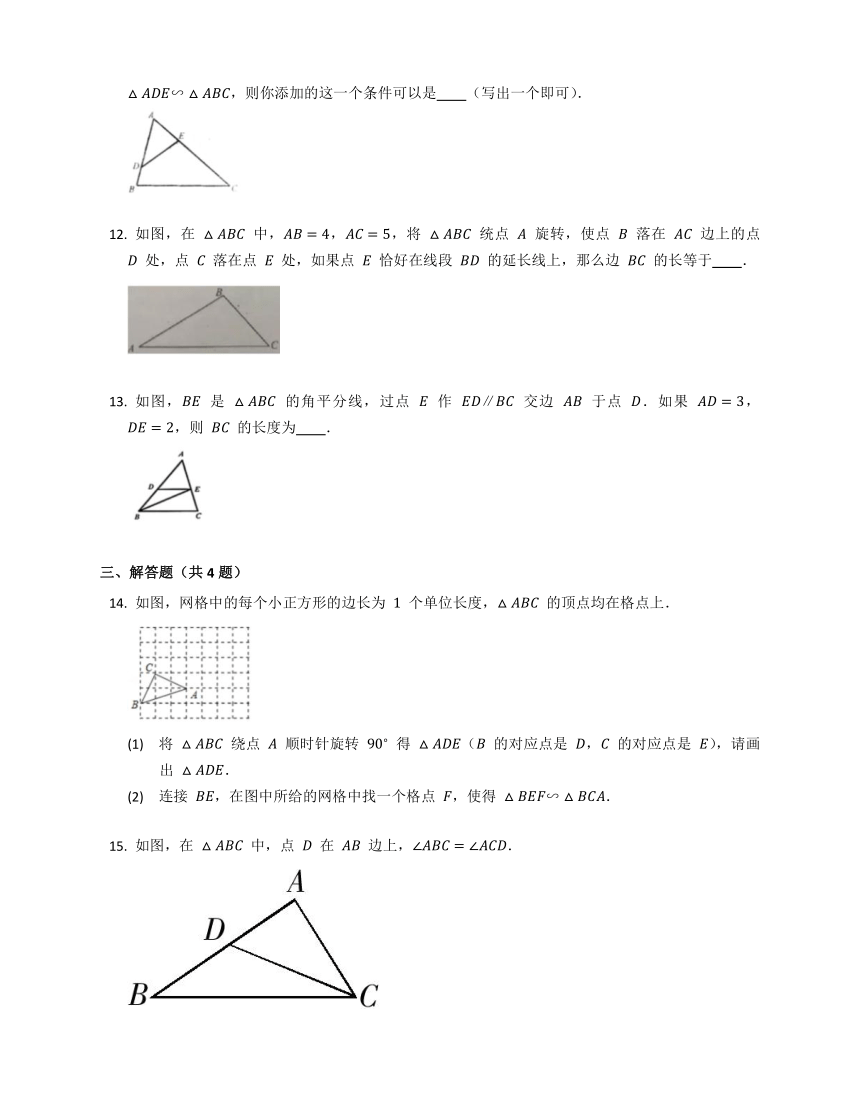
如图, 中,, 分别是 , 边上一点,连接 ,请你添加一个条件,使 ,则你添加的这一个条件可以是 (写出一个即可).
如图,在 中,,,将 统点 旋转,使点 落在 边上的点 处,点 落在点 处,如果点 恰好在线段 的延长线上,那么边 的长等于 .
如图, 是 的角平分线,过点 作 交边 于点 .如果 ,,则 的长度为 .
三、解答题(共4题)
如图,网格中的每个小正方形的边长为 个单位长度, 的顶点均在格点上.
(1) 将 绕点 顺时针旋转 得 ( 的对应点是 , 的对应点是 ),请画出 .
(2) 连接 ,在图中所给的网格中找一个格点 ,使得 .
如图,在 中,点 在 边上,.
(1) 求证:.
(2) 若 ,.求 的长.
尺规作图:如图.在 中,,.请用尺规在 上作点 ,并连接 ,使得 (保留作图痕迹,不要求写作法).
如图,已知 是 斜边 上的中线,过点 作 的平行线,过点 作 的垂线,两线相交于点 .
(1) 求证:;
(2) 若 ,,求 的面积.
答案
一、选择题(共10题)
1. 【答案】B
2. 【答案】C
【解析】由 ,,知 ,,对照四个选项知,C项中的三角形与 相似.
3. 【答案】C
【解析】
4. 【答案】A
5. 【答案】D
6. 【答案】D
【解析】因为 ,
所以 ,
因为 ,
所以 ,
所以 ,A正确,不符合题意.
因为 ,,
所以 ,B正确,不符合题意.
由三角形的面积公式得 ,
所以 ,C正确,不符合题意.
因为 ,,
所以 ,D错误,符合题意.
7. 【答案】D
8. 【答案】D
【解析】思路分析:“一线三等角”模型,根据“三垂直”关系找到相似是突破口.
如图,过点 作 ,交 于点 ,过点 作 ,交 于点 , 交 于点 .
四边形 是矩形,
,.
四边形 、四边形 都是平行四边形,
,.
又 ,
,
.
四边形 是矩形,
,,
,
,
,
,
,
.
故选:D.
9. 【答案】B
10. 【答案】B
【解析】思路分析:根据黄金分割的定义与黄金分割比解决即可.
,
,,
平分 ,
,
,
,
,
,
,
,
,,
,
,
,
点 是 边上的黄金分割点,,
,
.
故选:B.
二、填空题(共3题)
11. 【答案】 (或 ,)
12. 【答案】
【解析】如图所示,连接 ,
由旋转的性质可得:,,,,
,
又 ,
,
,即 ,
,
(负值已经舍去),
故答案为:.
13. 【答案】 或
【解析】 是 的角平分线,
,
,
,,
,
,
,
,,
,
,即 ,
解得:,
故答案为:.
三、解答题(共4题)
14. 【答案】
(1) 如图所示:,即为所求.
(2) 如图所示:.
15. 【答案】
(1) ,,
.
(2) ,
,
,,
,
.
16. 【答案】如图,点 即为所求.
17. 【答案】
(1) 是 斜边 上 的中线,
,
.
,
,
又 ,
.
(2) 在 中,.
是 斜边 上的中线,
.
,
,
的面积为 .
(共17题)
一、选择题(共10题)
如图,四边形 的对角线 , 相交于 ,且将这个四边形分成①,②,③,④四个三角形.若 ,则下列结论中一定正确的是
A.①和②相似 B.①和③相似 C.①和④相似 D.②和④相似
已知 如图所示,则下列 个三角形中,与 相似的是
A. B.
C. D.
若 是 的斜边 上异于 , 的一点,过点 作直线截 ,截得的三角形与原 相似,满足这样条件的直线共有
A. 条 B. 条 C. 条 D. 条
两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图, 是线段 上一点(),若满足 ,则称 是 的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长 米,主持人从舞台一侧进入,设他至少走 米时恰好站在舞台的黄金分割点上,则 满足的方程是
A. B.
C. D.以上都不对
如图,在 中,,,点 在 上,且 ,若要在 上找一点 ,使 与 相似,则 的长为
A. B. C. 或 D. 或
如图所示,在 中,, 于点 ,下列结论中错误的是
A. B.
C. D.
下列命题是真命题的为
A.同旁内角相等,两直线平行 B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形 D.两角分别相等的两个三角形相似
如图,在矩形 中,, 分别交 , 于点 ,, 分别交 , 于点 ,,若 ,,,则 的值为
A. B. C. D.
如图,已知 是半圆 的直径,弦 , 相交于点 ,若 ,那么 等于
A. B. C. D.
如图, 中,,, 的平分线 交 于点 ,若 ,则
A. B. C. D.
二、填空题(共3题)
如图, 中,, 分别是 , 边上一点,连接 ,请你添加一个条件,使 ,则你添加的这一个条件可以是 (写出一个即可).
如图,在 中,,,将 统点 旋转,使点 落在 边上的点 处,点 落在点 处,如果点 恰好在线段 的延长线上,那么边 的长等于 .
如图, 是 的角平分线,过点 作 交边 于点 .如果 ,,则 的长度为 .
三、解答题(共4题)
如图,网格中的每个小正方形的边长为 个单位长度, 的顶点均在格点上.
(1) 将 绕点 顺时针旋转 得 ( 的对应点是 , 的对应点是 ),请画出 .
(2) 连接 ,在图中所给的网格中找一个格点 ,使得 .
如图,在 中,点 在 边上,.
(1) 求证:.
(2) 若 ,.求 的长.
尺规作图:如图.在 中,,.请用尺规在 上作点 ,并连接 ,使得 (保留作图痕迹,不要求写作法).
如图,已知 是 斜边 上的中线,过点 作 的平行线,过点 作 的垂线,两线相交于点 .
(1) 求证:;
(2) 若 ,,求 的面积.
答案
一、选择题(共10题)
1. 【答案】B
2. 【答案】C
【解析】由 ,,知 ,,对照四个选项知,C项中的三角形与 相似.
3. 【答案】C
【解析】
4. 【答案】A
5. 【答案】D
6. 【答案】D
【解析】因为 ,
所以 ,
因为 ,
所以 ,
所以 ,A正确,不符合题意.
因为 ,,
所以 ,B正确,不符合题意.
由三角形的面积公式得 ,
所以 ,C正确,不符合题意.
因为 ,,
所以 ,D错误,符合题意.
7. 【答案】D
8. 【答案】D
【解析】思路分析:“一线三等角”模型,根据“三垂直”关系找到相似是突破口.
如图,过点 作 ,交 于点 ,过点 作 ,交 于点 , 交 于点 .
四边形 是矩形,
,.
四边形 、四边形 都是平行四边形,
,.
又 ,
,
.
四边形 是矩形,
,,
,
,
,
,
,
.
故选:D.
9. 【答案】B
10. 【答案】B
【解析】思路分析:根据黄金分割的定义与黄金分割比解决即可.
,
,,
平分 ,
,
,
,
,
,
,
,
,,
,
,
,
点 是 边上的黄金分割点,,
,
.
故选:B.
二、填空题(共3题)
11. 【答案】 (或 ,)
12. 【答案】
【解析】如图所示,连接 ,
由旋转的性质可得:,,,,
,
又 ,
,
,即 ,
,
(负值已经舍去),
故答案为:.
13. 【答案】 或
【解析】 是 的角平分线,
,
,
,,
,
,
,
,,
,
,即 ,
解得:,
故答案为:.
三、解答题(共4题)
14. 【答案】
(1) 如图所示:,即为所求.
(2) 如图所示:.
15. 【答案】
(1) ,,
.
(2) ,
,
,,
,
.
16. 【答案】如图,点 即为所求.
17. 【答案】
(1) 是 斜边 上 的中线,
,
.
,
,
又 ,
.
(2) 在 中,.
是 斜边 上的中线,
.
,
,
的面积为 .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
