山东省新泰市弘文高级中学2022-2023学年高一下学期6月月考数学试题(Word版含答案)
文档属性
| 名称 | 山东省新泰市弘文高级中学2022-2023学年高一下学期6月月考数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 457.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 15:54:22 | ||
图片预览


文档简介
弘文高级中学2022-2023学年高一下学期6月月考
数学试题
第I卷(选择题)
一、单选题
1.若,则z=( )
A.1–i B.1+i C.–i D.i
如图,在四面体ABCD中,E,F分别是AC与BD的中点,
若CD=2AB=4,EF⊥BA,则EF与CD所成的角为( )
A.90° B.45° C.60° D.30°
3.从数字中任取三个不同的数字,则所抽取的三个数字之和能被整除的概率为( )
A. B. C. D.
4.已知10个数据:4,5,6,7,8,8.5,9,10,11,11.5,则这组数据第40百分位数是( )
A.8 B.7 C.8.5 D.7.5
5.若圆锥的母线长为,侧面展开图的面积为,则该圆锥的体积是( )
A. B. C. D.
6.在发生某公共卫生事件期间,有专业机构认为该事件在一段事件内没有发生大规模群体感染的标志是“连续日,每天新增疑似病例不超过人”.过去日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:总体平均数为,中位数为; 乙地:总体平均数为,总体方差大于;
丙地:中位数为,众数为; 丁地:总体平均数为,总体方差为.
则甲、乙、丙、丁四地中,一定没有发生大规模群体感染的是( )
A.甲地 B.乙地 C.丙地 D.丁地
7.若是夹角为的两个单位向量,则与的夹角为( )
A.30° B.60° C.120° D.150°
我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童有外接球,且,,,,
平面与平面间的距离为,则该刍童外接球的体积为
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.甲乙两人独立的解题,已知各人能解出的概率分别是和,则题被解出的概率是
B.若,是互斥事件,则,
C.某校名教师的职称分布情况如下:高级占比,中级占比,初级占比,现从中抽取名教师做样本,若采用分层抽样方法,则高级教师应抽取人
D.一位男生和两位女生随机排成一列,则两位女生相邻的概率是
10.下列命题中是真命题的有( )
A.有A,B,C三种个体按的比例分层抽样调查,如果抽取的A个体数为9,则样本容量为30
B.一组数据1,2,3,3,4,5的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是甲
D.某一组样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在区间内的频率为
11.设复数在复平面内对应的点为Z,原点为O,为虚数单位,则下列说法正确的是( )
A.若,则或
B.若点Z的坐标为,且是关于的方程的一个根,
则
C.若,则的虚部为
D.若,则点的集合所构成的图形的面积为
12.在长方体中,已知,则下列结论正确的有( )
A. B.异面直线与所成的角为
C.二面角的余弦值为 D.四面体的体积为
第II卷(非选择题)
三、填空题
13.某工厂生产了一批节能灯泡,这批产品中按质量分为一等品,二等品,三等品.从这些产品中随机抽取一件产品测试,已知抽到一等品或二等品的概率为0.86,抽到二等品或三等品的概率为0.35,则抽到二等品的概率为___________.
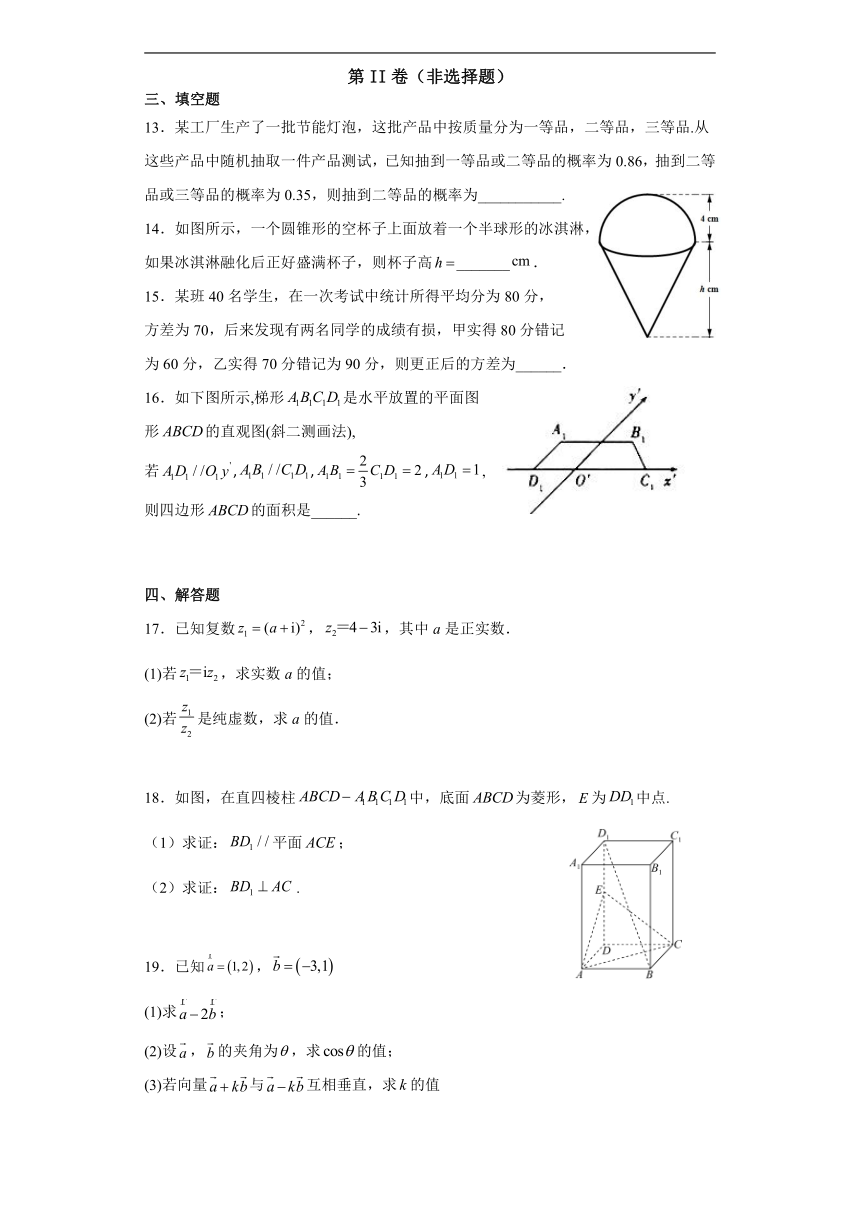
14.如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,
如果冰淇淋融化后正好盛满杯子,则杯子高_______.
某班40名学生,在一次考试中统计所得平均分为80分,
方差为70,后来发现有两名同学的成绩有损,甲实得80分错记
为60分,乙实得70分错记为90分,则更正后的方差为______.
如下图所示,梯形是水平放置的平面图
形的直观图(斜二测画法),
若,,,,
则四边形的面积是______.
四、解答题
17.已知复数,,其中a是正实数.
(1)若,求实数a的值;
(2)若是纯虚数,求a的值.
18.如图,在直四棱柱中,底面为菱形,为中点.
(1)求证:平面;
(2)求证:.
19.已知,
(1)求;
(2)设,的夹角为,求的值;
(3)若向量与互相垂直,求的值
某地教育部门对某学校学生的阅读素养进行检测,在该校随机抽取了名学生进行检测,实行百分制,现将所得的成绩按照分成6组,
并根据所得数据作出了如下所示的频数与频率的统计表
和频率分布直方图.
(1)求出表中及图中的值;
(2)(2)估计该校学生阅读素养的成绩中位数以及平均数.
21.计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依次为,,,在实际操作考试中“合格”的概率依次为,,,所有考试是否合格相互之间没有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
22.如图,在圆柱中,是圆柱的母线,是圆柱的底面的直径,是底面圆周上异于、的点.
(1)求证:平面;
(2)若,,,求圆柱的侧面积.
试卷第1页,共3页
弘文高级中学2022-2023学年高一下学期6月月考
数学答案
一单选题 DDCD BDCC
二多选题 9.BCD 10.BD 11.BD 12.ACD
三填空题 13.0.21 14.8 15.60 16.5
四解答题
17.【详解】(1)解:∵,,,
∴,从而,解得,
所以实数a的值为2.
(2)依题意得:,
因为是纯虚数,所以:,解得:或;
又因为a是正实数,所以a=2.
18.【详解】证明:(1)设与交于点,接,
底面是菱形,
为中点,
又因为是的中点,
,
面,平面
平面.
(2)底面是菱形,
,
底面,底面,
,且,平面.
平面.
平面,
.
19.【详解】(1)因为,,所以.
(2)因为,
所以.
(3)由,可得,
,
因为向量与互相垂直,
所以,
即,解得:.
20.【详解】(1);;
,解得.
(2)设中位数为,则,解得;
平均数为:.
21.【详解】(1)设“甲获得合格证书”为事件A,“乙获得合格证书”为事件B,“丙获得合格证书”为事件C,则,,.
因为,所以丙获得合格证书的可能性最大.
(2)设“三人考试后恰有两人获得合格证书”为事件D,则.
22.【详解】(1)证明:底面,且底面,
,
又,且,平面,
平面;
(2)在中,,,
,
又在中,,
.
圆柱的底面半径为,母线长为4,
圆柱的侧面积为.
数学试题
第I卷(选择题)
一、单选题
1.若,则z=( )
A.1–i B.1+i C.–i D.i
如图,在四面体ABCD中,E,F分别是AC与BD的中点,
若CD=2AB=4,EF⊥BA,则EF与CD所成的角为( )
A.90° B.45° C.60° D.30°
3.从数字中任取三个不同的数字,则所抽取的三个数字之和能被整除的概率为( )
A. B. C. D.
4.已知10个数据:4,5,6,7,8,8.5,9,10,11,11.5,则这组数据第40百分位数是( )
A.8 B.7 C.8.5 D.7.5
5.若圆锥的母线长为,侧面展开图的面积为,则该圆锥的体积是( )
A. B. C. D.
6.在发生某公共卫生事件期间,有专业机构认为该事件在一段事件内没有发生大规模群体感染的标志是“连续日,每天新增疑似病例不超过人”.过去日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:总体平均数为,中位数为; 乙地:总体平均数为,总体方差大于;
丙地:中位数为,众数为; 丁地:总体平均数为,总体方差为.
则甲、乙、丙、丁四地中,一定没有发生大规模群体感染的是( )
A.甲地 B.乙地 C.丙地 D.丁地
7.若是夹角为的两个单位向量,则与的夹角为( )
A.30° B.60° C.120° D.150°
我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童有外接球,且,,,,
平面与平面间的距离为,则该刍童外接球的体积为
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.甲乙两人独立的解题,已知各人能解出的概率分别是和,则题被解出的概率是
B.若,是互斥事件,则,
C.某校名教师的职称分布情况如下:高级占比,中级占比,初级占比,现从中抽取名教师做样本,若采用分层抽样方法,则高级教师应抽取人
D.一位男生和两位女生随机排成一列,则两位女生相邻的概率是
10.下列命题中是真命题的有( )
A.有A,B,C三种个体按的比例分层抽样调查,如果抽取的A个体数为9,则样本容量为30
B.一组数据1,2,3,3,4,5的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是甲
D.某一组样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在区间内的频率为
11.设复数在复平面内对应的点为Z,原点为O,为虚数单位,则下列说法正确的是( )
A.若,则或
B.若点Z的坐标为,且是关于的方程的一个根,
则
C.若,则的虚部为
D.若,则点的集合所构成的图形的面积为
12.在长方体中,已知,则下列结论正确的有( )
A. B.异面直线与所成的角为
C.二面角的余弦值为 D.四面体的体积为
第II卷(非选择题)
三、填空题
13.某工厂生产了一批节能灯泡,这批产品中按质量分为一等品,二等品,三等品.从这些产品中随机抽取一件产品测试,已知抽到一等品或二等品的概率为0.86,抽到二等品或三等品的概率为0.35,则抽到二等品的概率为___________.
14.如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,
如果冰淇淋融化后正好盛满杯子,则杯子高_______.
某班40名学生,在一次考试中统计所得平均分为80分,
方差为70,后来发现有两名同学的成绩有损,甲实得80分错记
为60分,乙实得70分错记为90分,则更正后的方差为______.
如下图所示,梯形是水平放置的平面图
形的直观图(斜二测画法),
若,,,,
则四边形的面积是______.
四、解答题
17.已知复数,,其中a是正实数.
(1)若,求实数a的值;
(2)若是纯虚数,求a的值.
18.如图,在直四棱柱中,底面为菱形,为中点.
(1)求证:平面;
(2)求证:.
19.已知,
(1)求;
(2)设,的夹角为,求的值;
(3)若向量与互相垂直,求的值
某地教育部门对某学校学生的阅读素养进行检测,在该校随机抽取了名学生进行检测,实行百分制,现将所得的成绩按照分成6组,
并根据所得数据作出了如下所示的频数与频率的统计表
和频率分布直方图.
(1)求出表中及图中的值;
(2)(2)估计该校学生阅读素养的成绩中位数以及平均数.
21.计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依次为,,,在实际操作考试中“合格”的概率依次为,,,所有考试是否合格相互之间没有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
22.如图,在圆柱中,是圆柱的母线,是圆柱的底面的直径,是底面圆周上异于、的点.
(1)求证:平面;
(2)若,,,求圆柱的侧面积.
试卷第1页,共3页
弘文高级中学2022-2023学年高一下学期6月月考
数学答案
一单选题 DDCD BDCC
二多选题 9.BCD 10.BD 11.BD 12.ACD
三填空题 13.0.21 14.8 15.60 16.5
四解答题
17.【详解】(1)解:∵,,,
∴,从而,解得,
所以实数a的值为2.
(2)依题意得:,
因为是纯虚数,所以:,解得:或;
又因为a是正实数,所以a=2.
18.【详解】证明:(1)设与交于点,接,
底面是菱形,
为中点,
又因为是的中点,
,
面,平面
平面.
(2)底面是菱形,
,
底面,底面,
,且,平面.
平面.
平面,
.
19.【详解】(1)因为,,所以.
(2)因为,
所以.
(3)由,可得,
,
因为向量与互相垂直,
所以,
即,解得:.
20.【详解】(1);;
,解得.
(2)设中位数为,则,解得;
平均数为:.
21.【详解】(1)设“甲获得合格证书”为事件A,“乙获得合格证书”为事件B,“丙获得合格证书”为事件C,则,,.
因为,所以丙获得合格证书的可能性最大.
(2)设“三人考试后恰有两人获得合格证书”为事件D,则.
22.【详解】(1)证明:底面,且底面,
,
又,且,平面,
平面;
(2)在中,,,
,
又在中,,
.
圆柱的底面半径为,母线长为4,
圆柱的侧面积为.
同课章节目录
