四川省眉山市2022-2023学年高二下学期期末考试数学(文)试题(Word版无答案)
文档属性
| 名称 | 四川省眉山市2022-2023学年高二下学期期末考试数学(文)试题(Word版无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 335.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 16:40:45 | ||
图片预览

文档简介
眉山市2022-2023学年高二下学期期末考试
数学试题卷(文史类)
2023.07
本试卷分为第I卷(选择题)和第II卷(非选择题).满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名.准考证号等填写在答题卷规定的位置上.
2.答选择题时,必须使用2B铅笔将答题卷上对应题目的答案标号涂黑.
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卷规定的位置上.
4.考试结束后,将答题卷交回.
第I卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求
1.若复数满足,则的虚部等于( )
A. B.3 C. D.
2.某学校为了解高二(1)班的30名的身体素质,将这些学生编号为1,2,…30,从这些学生中用系统抽样方法等距抽取5名学生进行体质测试.若20号学生被抽到,则下面4名学生中被抽到的是( )
A.5号学生 B.12号学生 C.14号学生 D.25号学生
3.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
A. B. C. D.
4.已知函数的图像在点处的切线方程是,则的值是( )
A. B. C. D.3
5.某市质量检测部门从辖区内甲、乙两个地区的食品生产企业中分别随机抽取9家企业,根据食品安全管理考核指标对抽到的企业进行考核,并将各企业考核得分整理成如下的茎叶图.由茎叶图所给信息,可判断以下结论中正确的是( )
A.若,则甲地区考核得分的方差小于乙地区考核得分的方差
B.若,则甲地区考核得分的极差大于乙地区考核得分的极差
C.若,则甲地区考核得分的中位数小于乙地区考核得分的中位数
D.若,则甲地区考核得分的平均数小于乙地区考核得分的平均数
6.已知函数的导函数为,且,则( )
A. B. C. D.
7.用秦九韶算法求多项式在时,的值为( )
A.136 B.45 C.27 D.14
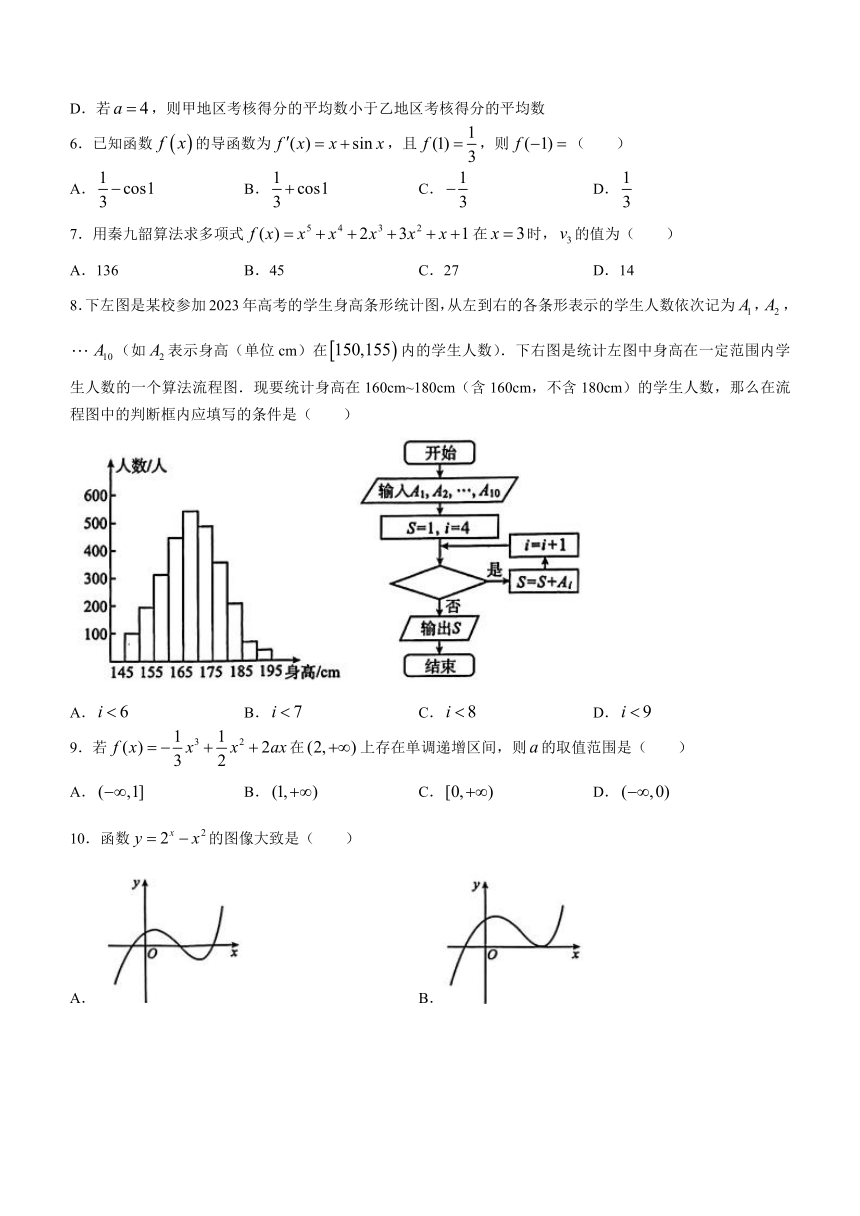
8.下左图是某校参加2023年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为,,(如表示身高(单位cm)在内的学生人数).下右图是统计左图中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160cm~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )
A. B. C. D.
9.若在上存在单调递增区间,则的取值范围是( )
A. B. C. D.
10.函数的图像大致是( )
A. B.
C. D.
11.函数的定义域是,,对任意,,则不等式的解集为( )
A. B.
C. D.
12.已知,,,则( )
A. B. C. D.
第II卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卷中的相应位置.
13.化为十进制数为________.
14.18世纪数学家欧拉研究调和级数得到了以下的结果:当很大时,(常数).利用以上公式,可以估计的值为________.
15.已知、都是定义在上的函数,,,,,则关于的方程没有实数根的概率为________.
16.已知函数,给出下列命题:
①该函数必有2个极值;
②该函数的极大值必大于1;
③该函数的极小值必小于1;
④方程一定有三个不等的实数根.
则正确的命题序号是________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
眉山市丹棱县柑橘桃闻名中外.某柑橘专业户计划种植、两种柑橘品种,通过大量考察研究得到如下统计数据.柑橘的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
年份 2018 2019 2020 2021 2022
年份编号 1 2 3 4 5
单价(元/公斤) 18 20 23 25 29
柑橘亩产量的频率分布直方图如图所示:
(1)若柑橘的单价(单位:元/公斤)与年份编号间具有线性相关关系;请求出关于的回归直线方程,并估计2023年柑橘的单价;
(2)利用上述频率分布直方图估计柑橘的平均亩产量(同一组数据用中点值为代表);
参考公式:回归直线方程,其中,
18.(本小题满分12分)
已知函数在处有极值10.
(1)求实数,的值;
(2)若方程在区间内有解,求实数的取值范围.
19.(本小题满分12分)
已知关于的一元二次方程
(1)若,是一枚骰子掷两次所得到的点数,求方程有两正根的概率.
(2)若,,求方程没有实根的概率.
20.(本小题满分12分)
某中学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢荤食 不喜欢荤食 合计
男生 60 20 80
女生 10 10 20
合计 70 30 100
(1)根据表中数据,问是否有95%的把握认为“男生和女生在选用荤食的饮食习惯方面有差异”;
(2)已知在被调查的男生中有5名选课“物理+化学+生物”方向的学生,其中2名喜欢荤食,现在从这5名学生中随机抽取3人,求至多有1人喜欢荤食的概率.
参考公式:,其中.
21.(本小题满分12分)
已知函数.
(1)当时,求在点处的切线方程;
(2)若对任意,都有恒成立,求的取值范围.
22.(本小题满分12分)
已知函数,其中为自然对数的底数.
(1)当时,证明:;
(2)当时,求函数零点个数.
数学试题卷(文史类)
2023.07
本试卷分为第I卷(选择题)和第II卷(非选择题).满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名.准考证号等填写在答题卷规定的位置上.
2.答选择题时,必须使用2B铅笔将答题卷上对应题目的答案标号涂黑.
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卷规定的位置上.
4.考试结束后,将答题卷交回.
第I卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求
1.若复数满足,则的虚部等于( )
A. B.3 C. D.
2.某学校为了解高二(1)班的30名的身体素质,将这些学生编号为1,2,…30,从这些学生中用系统抽样方法等距抽取5名学生进行体质测试.若20号学生被抽到,则下面4名学生中被抽到的是( )
A.5号学生 B.12号学生 C.14号学生 D.25号学生
3.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
A. B. C. D.
4.已知函数的图像在点处的切线方程是,则的值是( )
A. B. C. D.3
5.某市质量检测部门从辖区内甲、乙两个地区的食品生产企业中分别随机抽取9家企业,根据食品安全管理考核指标对抽到的企业进行考核,并将各企业考核得分整理成如下的茎叶图.由茎叶图所给信息,可判断以下结论中正确的是( )
A.若,则甲地区考核得分的方差小于乙地区考核得分的方差
B.若,则甲地区考核得分的极差大于乙地区考核得分的极差
C.若,则甲地区考核得分的中位数小于乙地区考核得分的中位数
D.若,则甲地区考核得分的平均数小于乙地区考核得分的平均数
6.已知函数的导函数为,且,则( )
A. B. C. D.
7.用秦九韶算法求多项式在时,的值为( )
A.136 B.45 C.27 D.14
8.下左图是某校参加2023年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为,,(如表示身高(单位cm)在内的学生人数).下右图是统计左图中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160cm~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )
A. B. C. D.
9.若在上存在单调递增区间,则的取值范围是( )
A. B. C. D.
10.函数的图像大致是( )
A. B.
C. D.
11.函数的定义域是,,对任意,,则不等式的解集为( )
A. B.
C. D.
12.已知,,,则( )
A. B. C. D.
第II卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填在答题卷中的相应位置.
13.化为十进制数为________.
14.18世纪数学家欧拉研究调和级数得到了以下的结果:当很大时,(常数).利用以上公式,可以估计的值为________.
15.已知、都是定义在上的函数,,,,,则关于的方程没有实数根的概率为________.
16.已知函数,给出下列命题:
①该函数必有2个极值;
②该函数的极大值必大于1;
③该函数的极小值必小于1;
④方程一定有三个不等的实数根.
则正确的命题序号是________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
眉山市丹棱县柑橘桃闻名中外.某柑橘专业户计划种植、两种柑橘品种,通过大量考察研究得到如下统计数据.柑橘的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
年份 2018 2019 2020 2021 2022
年份编号 1 2 3 4 5
单价(元/公斤) 18 20 23 25 29
柑橘亩产量的频率分布直方图如图所示:
(1)若柑橘的单价(单位:元/公斤)与年份编号间具有线性相关关系;请求出关于的回归直线方程,并估计2023年柑橘的单价;
(2)利用上述频率分布直方图估计柑橘的平均亩产量(同一组数据用中点值为代表);
参考公式:回归直线方程,其中,
18.(本小题满分12分)
已知函数在处有极值10.
(1)求实数,的值;
(2)若方程在区间内有解,求实数的取值范围.
19.(本小题满分12分)
已知关于的一元二次方程
(1)若,是一枚骰子掷两次所得到的点数,求方程有两正根的概率.
(2)若,,求方程没有实根的概率.
20.(本小题满分12分)
某中学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢荤食 不喜欢荤食 合计
男生 60 20 80
女生 10 10 20
合计 70 30 100
(1)根据表中数据,问是否有95%的把握认为“男生和女生在选用荤食的饮食习惯方面有差异”;
(2)已知在被调查的男生中有5名选课“物理+化学+生物”方向的学生,其中2名喜欢荤食,现在从这5名学生中随机抽取3人,求至多有1人喜欢荤食的概率.
参考公式:,其中.
21.(本小题满分12分)
已知函数.
(1)当时,求在点处的切线方程;
(2)若对任意,都有恒成立,求的取值范围.
22.(本小题满分12分)
已知函数,其中为自然对数的底数.
(1)当时,证明:;
(2)当时,求函数零点个数.
同课章节目录
