数学五年级上北师大版6.1组合图形的面积课件
文档属性
| 名称 | 数学五年级上北师大版6.1组合图形的面积课件 |  | |
| 格式 | zip | ||
| 文件大小 | 253.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-31 08:18:06 | ||
图片预览




文档简介
课件13张PPT。欢迎同学们,家长们
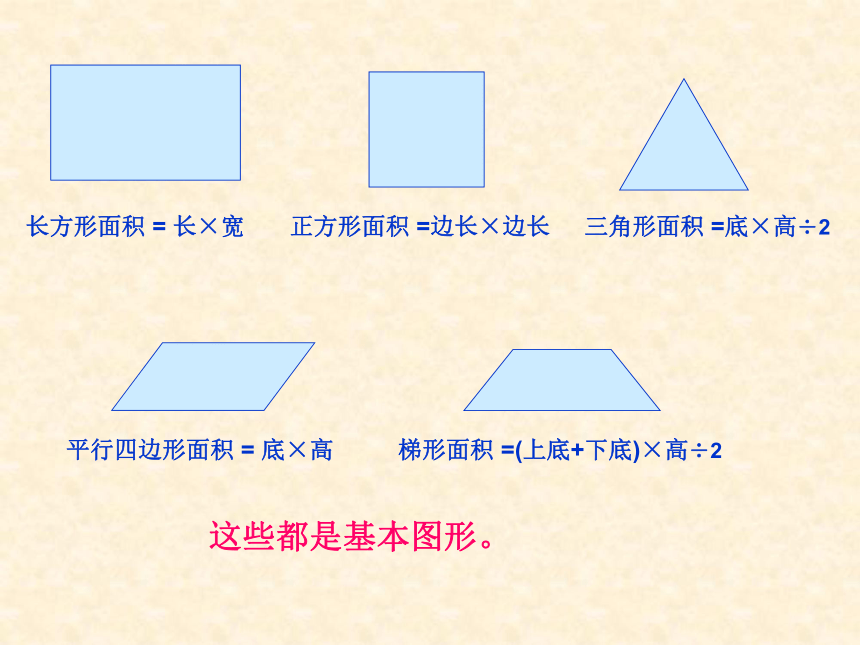
一起进入我们的课堂!长方形面积 = 长×宽正方形面积 =边长×边长三角形面积 =底×高÷2平行四边形面积 = 底×高梯形面积 =(上底+下底)×高÷2这些都是基本图形。这些图形你认识吗?组合图形面积你能给这类图形取个名字吗?拼图活动1、请同学们拿出材料中的5个基本图形,任选2个或3个拼成一个你喜欢的组合图形。
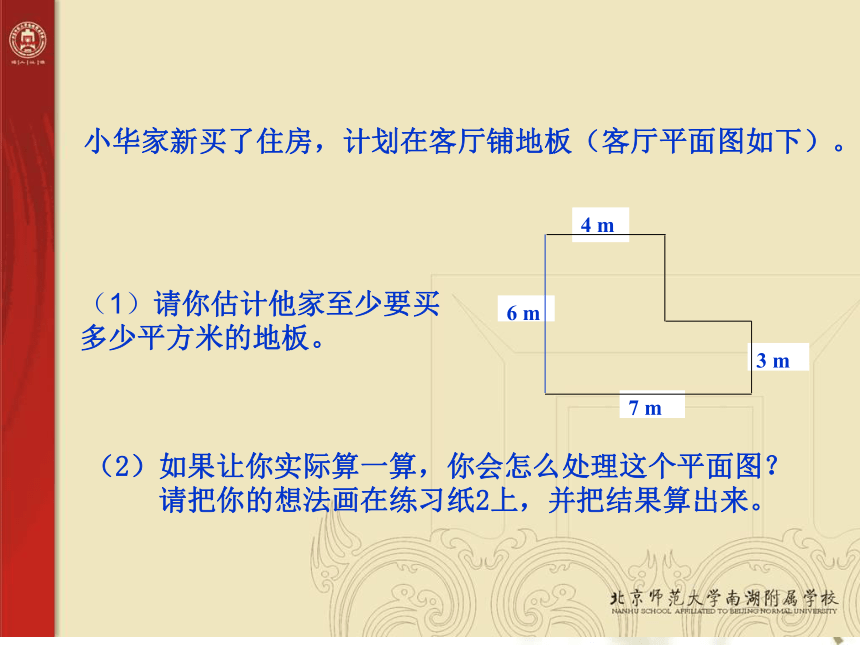
2、把你们拼成的组合图形画在练习纸1上。 小华家新买了住房,计划在客厅铺地板(客厅平面图如下)。(1)请你估计他家至少要买多少平方米的地板。(2)如果让你实际算一算,你会怎么处理这个平面图?
请把你的想法画在练习纸2上,并把结果算出来。怎样把这个图形转化成已学过的图形?7 m3 m6 m4 m分割法添补法方法一:分割成两个长方形方法二:分割成一个长方形
和一个正方形方法三:分割成两个梯形方法四:补上一个小正方形,使它成为一个大长方形 7×3 + 4×3
= 21 + 12
= 33(m2) 4×6+3×3
= 24 + 9
= 33(m2)(3+6)×4÷2 + (3+7)×3÷2
= 9×4÷2 + 10×3÷2
= 33(m2)7×6 —3×3
= 42—9
= 33(m2)方法一:分割成两个长方形方法二:分割成一个长方形和一个正方形方法三:分割成两个梯形方法四:补上一个小正方形,使它成为一个大长方形6—3=3(m)7—4=3(m)3m3m3m3m答:至少要33平方米的地板。答:至少要33平方米的地板。答:至少要33平方米的地板。答:至少要33平方米的地板。找出对应条件计算 计算组合图形的面积主要可以采用“分割”
与“添补”的方法进行计算。通过刚才的学习,你认为应怎样计算组合图形的面积?
1、求下列图形的面积。(单位:cm)
50×33 + 35×12÷2
= 1650 + 210
= 1860(m2)课堂练习答:新丰小学这块菜地的面积是1860平方米。201016求下列图形的面积。(单位:cm)12(10+16) ×12÷220×(16-10) ÷2+=156+60=216(cm2)
如图,一张硬纸板剪下4个边长是4厘米的小正方形后,
可以做成一个没有盖子的盒子。这张硬纸板还剩下多大的面积?
试一试:4cm方法1:26×20—4×4×4
= 520—64
= 456(cm2)方法2:26×(20— 4×2)=312(cm2)
(26— 4×2)×4×2=144( cm2 )
312 + 144 = 456 (cm2) 方法3:20×(26—4×2)=360 (cm2)
(20— 4×2)×4×2=96( cm2 )
360+ 96 = 456 (cm2) 答:这张硬纸板还剩下456cm2。答:这张硬纸板还剩下456cm2。答:这张硬纸板还剩下456cm2。小 结关键词: 组合图形 转化
分割法 添补法
如何求组合图形的面积?
一起进入我们的课堂!长方形面积 = 长×宽正方形面积 =边长×边长三角形面积 =底×高÷2平行四边形面积 = 底×高梯形面积 =(上底+下底)×高÷2这些都是基本图形。这些图形你认识吗?组合图形面积你能给这类图形取个名字吗?拼图活动1、请同学们拿出材料中的5个基本图形,任选2个或3个拼成一个你喜欢的组合图形。
2、把你们拼成的组合图形画在练习纸1上。 小华家新买了住房,计划在客厅铺地板(客厅平面图如下)。(1)请你估计他家至少要买多少平方米的地板。(2)如果让你实际算一算,你会怎么处理这个平面图?
请把你的想法画在练习纸2上,并把结果算出来。怎样把这个图形转化成已学过的图形?7 m3 m6 m4 m分割法添补法方法一:分割成两个长方形方法二:分割成一个长方形
和一个正方形方法三:分割成两个梯形方法四:补上一个小正方形,使它成为一个大长方形 7×3 + 4×3
= 21 + 12
= 33(m2) 4×6+3×3
= 24 + 9
= 33(m2)(3+6)×4÷2 + (3+7)×3÷2
= 9×4÷2 + 10×3÷2
= 33(m2)7×6 —3×3
= 42—9
= 33(m2)方法一:分割成两个长方形方法二:分割成一个长方形和一个正方形方法三:分割成两个梯形方法四:补上一个小正方形,使它成为一个大长方形6—3=3(m)7—4=3(m)3m3m3m3m答:至少要33平方米的地板。答:至少要33平方米的地板。答:至少要33平方米的地板。答:至少要33平方米的地板。找出对应条件计算 计算组合图形的面积主要可以采用“分割”
与“添补”的方法进行计算。通过刚才的学习,你认为应怎样计算组合图形的面积?
1、求下列图形的面积。(单位:cm)
50×33 + 35×12÷2
= 1650 + 210
= 1860(m2)课堂练习答:新丰小学这块菜地的面积是1860平方米。201016求下列图形的面积。(单位:cm)12(10+16) ×12÷220×(16-10) ÷2+=156+60=216(cm2)
如图,一张硬纸板剪下4个边长是4厘米的小正方形后,
可以做成一个没有盖子的盒子。这张硬纸板还剩下多大的面积?
试一试:4cm方法1:26×20—4×4×4
= 520—64
= 456(cm2)方法2:26×(20— 4×2)=312(cm2)
(26— 4×2)×4×2=144( cm2 )
312 + 144 = 456 (cm2) 方法3:20×(26—4×2)=360 (cm2)
(20— 4×2)×4×2=96( cm2 )
360+ 96 = 456 (cm2) 答:这张硬纸板还剩下456cm2。答:这张硬纸板还剩下456cm2。答:这张硬纸板还剩下456cm2。小 结关键词: 组合图形 转化
分割法 添补法
如何求组合图形的面积?
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
