八年级数学上册北师大版《6.2 中位数与众数》教学课件(共27张ppt)
文档属性
| 名称 | 八年级数学上册北师大版《6.2 中位数与众数》教学课件(共27张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 962.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 09:20:04 | ||
图片预览








文档简介
(共27张PPT)
6.2 中位数与众数
第六章 数据的分析
1.经历用中位数和众数描述数据集中趋势的过程,发展数据分析观念.
2.理解中位数和众数的概念,能求出一组数据的中位数和众数.
3.在具体情景中体会平均数、中位数和众数三者的差别,能根据问题的背景选择合适的量描述一组数据的集中趋势.
学习目标
在当今信息时代,信息的重要性不言而喻,人们经常要求一些信息“用数据说话”,所以对数据作出恰当的评判是很重要的,平均数是我们常用的一个数据代表,但是平均数容易受到极端数据的影响,反应问题会出现偏差.
情境引入
某次数学考试,小英得了78分.全班共32人,其他同学的成绩为1个100分,4个90分,22个80分,2个62分,1个30分,1个25分.
小英计算出全班的平均分为77.4分,所以小英告诉妈妈说,自己这次数学成绩在班上处于“中上水平”.小英对妈妈说的情况属实吗?你对此有何看法?
情境引入
平均数是我们常用的一个数据代表,但是在这里,利用平均数把倒数第五的成绩说成处于班级的“中上水平”显然是不属实的.原因是全班的平均分受到了两个极端数据30分和25分的影响,利用平均数反应问题就出现了偏差.
怎样解决这个问题呢?我们需要学习新的数据代表——中位数与众数.
情境引入
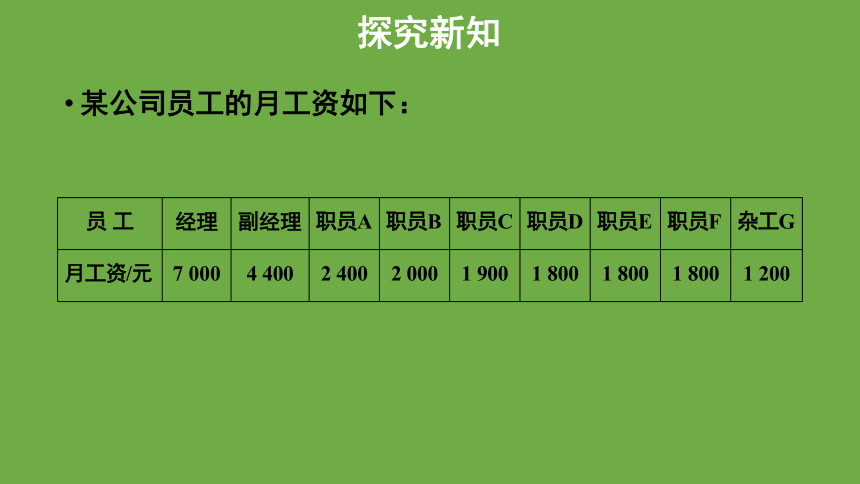
某公司员工的月工资如下:
员 工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7 000 4 400 2 400 2 000 1 900 1 800 1 800 1 800 1 200
探究新知
我们公司员工收入很高,月平均工资为2 700元.
我的工资是1 900元,在公司算是中等收入.
我们好几个人工资都是1 800元.
这个公司员工收入到底怎样呢?
经理
职员C
职员D
应聘者
探究新知
你怎样看待该公司员工的收入?
上述问题中,经理、职员C、职员D从不同的角度描述了该公司的收入情况:
(1)月平均工资2 700元,指所有员工工资的平均数是2 700元,但只有正、副经理的工资比平均工资高,是他两人的工资把平均工资“拉”高了.
(2)职员C的工资是1 900元,恰好居于所有员工工资的“正中间”(恰有4人的工资比他高,有4人的工资比他低),我们称1 900元是这组数据的中位数.
(3)9个员工中有3个人的工资为1 800元,出现的次数最多,我们称 1 800元是这组数据的众数.
探究新知
议一议:你认为用哪个数据表示该公司员工收入的平均水平更合适?
用中位数1 900元或众数1 800元表示该公司员工收入的平均水平更合适些,因为平均数2 700元受到了极端值的影响.
探究新知
一般地,n个数据按大小顺序排列,处于最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
一组数据中出现次数最多的那个数据叫做这组数据的众数.
探究新知
1.对于一组数据:3,3,2,3,6,3,10,3,6,3,2,下列说法正确的是( )
A.这组数据的众数是3
B.这组数据的众数与中位数的数值不等
C.这组数据的中位数与平均数的数值相等
D.这组数据的平均数与众数的数值相等
A
运用提高
2.你课前所调查的50名男同学所穿运动鞋尺码的平均数、中位数、众数分别是多少?你认为学校商店应多进哪种尺码的男式运动鞋?
运用提高
应多进众数所在尺码的男式运动鞋。
例 某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1 800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
典例精讲
解:(1)平均数为:
中位数为:210(件),众数为:210(件).
(2)不合理.
因为15人中有13人的销售额达不到320件,(320虽是所给一组数据的平均数,它却不能反映营销人员的一般水平).
销售额定为210件合适一些,因为210既是中位数,又是众数,是大部分人能达到的定额.
典例精讲
=320(件)
1.数据1,2,8,5,3,9,5,4,5,4的众数、中位数分别为( )
A.4.5、 5 B.5、 4.5 C.5、 4 D.5、 5
2.婷婷的妈妈是一位校鞋经销部的经理,为了解鞋子的销售情况,随机调查了9位学生的鞋子的尺码,由小到大是:20,21,21,22,22,22,22,23,23.对这组数据的分析中,婷婷的妈妈最感兴趣的数据代表是( )
A.平均数 B.中位数 C.众数
B
C
课堂练习
3.我市电视台举办的歌手大奖赛上,八位评委给某位歌手的评分如下:90,91,94,95,95,96,96,97.这组数据的众数是( )
A.95 B.96 C.2 D.95和96
4.甲乙丙丁四支足球队在全国甲级联赛中进球数分别为:9,9,x,7,若这组数据的众数与平均数恰好相等,则这组数据的中位数是( )
A.10 B.9 C.8 D.7
D
B
课堂练习
5.把5个整数从小到大排列,其中位数是4,如果这5个整数中的惟一众数是6,则这5个整数可能的最大的和是( )
A.21 B.22 C.23 D.24
A
6.为了迎接2008年奥运会,某单位举办了英语培训班.100名职工在一个月内参加英语培训的次数如图:
这个月职工平均参加英语培训的次数是__________,这个月每名职工参加英语培训次数的众数为__________,中位数是__________.
6次
6次
6次
课堂练习
绿地面积(公顷)
年份
60
56
51
48
2016
2015
2014
2013
7.某市为美化城区,改善人们的居住环境,近几年,植树种草、修建公园,使绿地面积不断增加,如图:
课堂练习
(1)根据图中所提供的信息,回答下列问题:2015年底的绿地面积为_________公顷,比2014年底增加了_________公顷;在2014年、2015年、2016年这三年中,绿地面积增加最多的是_________年.
(2)为满足城市发展的需要,计划到2018年底使城区绿地面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
56
5
2015
课堂练习
(2)设今明两年绿地面积的年平均增长率x.
则60(1+x)2=72.6.
解得x=10%.
绿地面积(公顷)
年份
60
56
51
48
2016
2015
2014
2013
课堂练习
接触中考
8.某中学为了了解全校的耗电情况,抽查了10 天中全校每天的耗电量,数据如下表:(单位:kw·h)
耗电量/kw·h) 90 93 102 113 114 120
天数 1 1 2 3 1 2
(1)写出上表中数据的众数和平均数;
(2)由上题获得的数据,估计该校某月的耗电量(按30天计);
(3)若当地每度电的定价是0.5元,写出该校应付电费y(元)与天数x 之间的函数关系式.
解:(1)众数为113(kwh);平均数 =108kw·h
(2)某月耗电量Q=108×30=3240kw·h
(3)y=0.5×108x,即y=54x
接触中考
9.随机抽取某城市一年(以365天计)中的30天的日平均气温状况统计如下:
温度(x℃) 10 14 18 22 26 30 32
天数t 3 5 5 7 6 2 2
请根据上述数据填空:
(1)该组数据的中位数是________.
(2)该城市一年中日平均气温为26℃的约有_____天.
(3)若日平均气温在17℃~23℃为市民“满意温度”,则该城市一年中达到市民“满意温度”的约有______天.
22℃
73
146
接触中考
10.2002年世界杯足球赛时,中国队首场比赛的首发阵容名单和他们的身高如下表所示:
姓名 当津 李玮峰 范志毅 吴孙瑛 孙继海 李铁
身高(米) 1.98 1.82 1.83 1.83 1.83 1.83
姓名 马明宇 李小鹏 徐云龙 杨晨 郝海东
身高(米) 1.76 1.82 1.81 1.85 1.80
则这些动员员的身高的众数和中位数分别是__________.
1.83,1.83
接触中考
1.用平均数作为一组数据的代表,比较可靠和稳定,它与这组数据中的每一个数都有关系,对这组数据所包含的信息的反映最为充分,因此在现实生活中较为常用,但它容易受极端值的影响.
课堂小结
2.用中位数作为一组数据的代表,可靠性比较差,它不能充分利用所有数据的信息,但它不受极端值的影响,当一组数据中有个别数据变动较大时,可用它来描述这组数据的“集中趋势”.
3.用众数作为一组数据的代表,可靠性也比较差,其大小只与这组数据中的部分数据有关,但它不受极端值的影响.当一组数据中某些数据多次重复出现时,众数往往是人们尤为关心的一种统计量.要根据不同的实际需要,确定是用平均数、中位数还是众数来反映数据的平均水平.
课堂小结
再见
6.2 中位数与众数
第六章 数据的分析
1.经历用中位数和众数描述数据集中趋势的过程,发展数据分析观念.
2.理解中位数和众数的概念,能求出一组数据的中位数和众数.
3.在具体情景中体会平均数、中位数和众数三者的差别,能根据问题的背景选择合适的量描述一组数据的集中趋势.
学习目标
在当今信息时代,信息的重要性不言而喻,人们经常要求一些信息“用数据说话”,所以对数据作出恰当的评判是很重要的,平均数是我们常用的一个数据代表,但是平均数容易受到极端数据的影响,反应问题会出现偏差.
情境引入
某次数学考试,小英得了78分.全班共32人,其他同学的成绩为1个100分,4个90分,22个80分,2个62分,1个30分,1个25分.
小英计算出全班的平均分为77.4分,所以小英告诉妈妈说,自己这次数学成绩在班上处于“中上水平”.小英对妈妈说的情况属实吗?你对此有何看法?
情境引入
平均数是我们常用的一个数据代表,但是在这里,利用平均数把倒数第五的成绩说成处于班级的“中上水平”显然是不属实的.原因是全班的平均分受到了两个极端数据30分和25分的影响,利用平均数反应问题就出现了偏差.
怎样解决这个问题呢?我们需要学习新的数据代表——中位数与众数.
情境引入
某公司员工的月工资如下:
员 工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7 000 4 400 2 400 2 000 1 900 1 800 1 800 1 800 1 200
探究新知
我们公司员工收入很高,月平均工资为2 700元.
我的工资是1 900元,在公司算是中等收入.
我们好几个人工资都是1 800元.
这个公司员工收入到底怎样呢?
经理
职员C
职员D
应聘者
探究新知
你怎样看待该公司员工的收入?
上述问题中,经理、职员C、职员D从不同的角度描述了该公司的收入情况:
(1)月平均工资2 700元,指所有员工工资的平均数是2 700元,但只有正、副经理的工资比平均工资高,是他两人的工资把平均工资“拉”高了.
(2)职员C的工资是1 900元,恰好居于所有员工工资的“正中间”(恰有4人的工资比他高,有4人的工资比他低),我们称1 900元是这组数据的中位数.
(3)9个员工中有3个人的工资为1 800元,出现的次数最多,我们称 1 800元是这组数据的众数.
探究新知
议一议:你认为用哪个数据表示该公司员工收入的平均水平更合适?
用中位数1 900元或众数1 800元表示该公司员工收入的平均水平更合适些,因为平均数2 700元受到了极端值的影响.
探究新知
一般地,n个数据按大小顺序排列,处于最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
一组数据中出现次数最多的那个数据叫做这组数据的众数.
探究新知
1.对于一组数据:3,3,2,3,6,3,10,3,6,3,2,下列说法正确的是( )
A.这组数据的众数是3
B.这组数据的众数与中位数的数值不等
C.这组数据的中位数与平均数的数值相等
D.这组数据的平均数与众数的数值相等
A
运用提高
2.你课前所调查的50名男同学所穿运动鞋尺码的平均数、中位数、众数分别是多少?你认为学校商店应多进哪种尺码的男式运动鞋?
运用提高
应多进众数所在尺码的男式运动鞋。
例 某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1 800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
典例精讲
解:(1)平均数为:
中位数为:210(件),众数为:210(件).
(2)不合理.
因为15人中有13人的销售额达不到320件,(320虽是所给一组数据的平均数,它却不能反映营销人员的一般水平).
销售额定为210件合适一些,因为210既是中位数,又是众数,是大部分人能达到的定额.
典例精讲
=320(件)
1.数据1,2,8,5,3,9,5,4,5,4的众数、中位数分别为( )
A.4.5、 5 B.5、 4.5 C.5、 4 D.5、 5
2.婷婷的妈妈是一位校鞋经销部的经理,为了解鞋子的销售情况,随机调查了9位学生的鞋子的尺码,由小到大是:20,21,21,22,22,22,22,23,23.对这组数据的分析中,婷婷的妈妈最感兴趣的数据代表是( )
A.平均数 B.中位数 C.众数
B
C
课堂练习
3.我市电视台举办的歌手大奖赛上,八位评委给某位歌手的评分如下:90,91,94,95,95,96,96,97.这组数据的众数是( )
A.95 B.96 C.2 D.95和96
4.甲乙丙丁四支足球队在全国甲级联赛中进球数分别为:9,9,x,7,若这组数据的众数与平均数恰好相等,则这组数据的中位数是( )
A.10 B.9 C.8 D.7
D
B
课堂练习
5.把5个整数从小到大排列,其中位数是4,如果这5个整数中的惟一众数是6,则这5个整数可能的最大的和是( )
A.21 B.22 C.23 D.24
A
6.为了迎接2008年奥运会,某单位举办了英语培训班.100名职工在一个月内参加英语培训的次数如图:
这个月职工平均参加英语培训的次数是__________,这个月每名职工参加英语培训次数的众数为__________,中位数是__________.
6次
6次
6次
课堂练习
绿地面积(公顷)
年份
60
56
51
48
2016
2015
2014
2013
7.某市为美化城区,改善人们的居住环境,近几年,植树种草、修建公园,使绿地面积不断增加,如图:
课堂练习
(1)根据图中所提供的信息,回答下列问题:2015年底的绿地面积为_________公顷,比2014年底增加了_________公顷;在2014年、2015年、2016年这三年中,绿地面积增加最多的是_________年.
(2)为满足城市发展的需要,计划到2018年底使城区绿地面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
56
5
2015
课堂练习
(2)设今明两年绿地面积的年平均增长率x.
则60(1+x)2=72.6.
解得x=10%.
绿地面积(公顷)
年份
60
56
51
48
2016
2015
2014
2013
课堂练习
接触中考
8.某中学为了了解全校的耗电情况,抽查了10 天中全校每天的耗电量,数据如下表:(单位:kw·h)
耗电量/kw·h) 90 93 102 113 114 120
天数 1 1 2 3 1 2
(1)写出上表中数据的众数和平均数;
(2)由上题获得的数据,估计该校某月的耗电量(按30天计);
(3)若当地每度电的定价是0.5元,写出该校应付电费y(元)与天数x 之间的函数关系式.
解:(1)众数为113(kwh);平均数 =108kw·h
(2)某月耗电量Q=108×30=3240kw·h
(3)y=0.5×108x,即y=54x
接触中考
9.随机抽取某城市一年(以365天计)中的30天的日平均气温状况统计如下:
温度(x℃) 10 14 18 22 26 30 32
天数t 3 5 5 7 6 2 2
请根据上述数据填空:
(1)该组数据的中位数是________.
(2)该城市一年中日平均气温为26℃的约有_____天.
(3)若日平均气温在17℃~23℃为市民“满意温度”,则该城市一年中达到市民“满意温度”的约有______天.
22℃
73
146
接触中考
10.2002年世界杯足球赛时,中国队首场比赛的首发阵容名单和他们的身高如下表所示:
姓名 当津 李玮峰 范志毅 吴孙瑛 孙继海 李铁
身高(米) 1.98 1.82 1.83 1.83 1.83 1.83
姓名 马明宇 李小鹏 徐云龙 杨晨 郝海东
身高(米) 1.76 1.82 1.81 1.85 1.80
则这些动员员的身高的众数和中位数分别是__________.
1.83,1.83
接触中考
1.用平均数作为一组数据的代表,比较可靠和稳定,它与这组数据中的每一个数都有关系,对这组数据所包含的信息的反映最为充分,因此在现实生活中较为常用,但它容易受极端值的影响.
课堂小结
2.用中位数作为一组数据的代表,可靠性比较差,它不能充分利用所有数据的信息,但它不受极端值的影响,当一组数据中有个别数据变动较大时,可用它来描述这组数据的“集中趋势”.
3.用众数作为一组数据的代表,可靠性也比较差,其大小只与这组数据中的部分数据有关,但它不受极端值的影响.当一组数据中某些数据多次重复出现时,众数往往是人们尤为关心的一种统计量.要根据不同的实际需要,确定是用平均数、中位数还是众数来反映数据的平均水平.
课堂小结
再见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
