八年级数学上册北师大版《1.2 一定是直角三角形吗》教学课件(共23张ppt)
文档属性
| 名称 | 八年级数学上册北师大版《1.2 一定是直角三角形吗》教学课件(共23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 996.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 09:23:05 | ||
图片预览








文档简介
(共23张PPT)
第一章探索勾股定理
1.2一定是直角三角形吗
学习目标
1.掌握直角三角形的判别条件,掌握常见的勾股数.
2.经历直角三角形的判别条件的探索过程,并能进行简单的应用.
复习回顾
直角三角形有哪些性质?
①有一个内角为直角;
②两个锐角互余;
③两条直角边的平方和等于斜边的平方.
复习回顾
【问题】
一个三角形,满足什么条件时是直角三角形呢?
探究新知
拿出事先准备好的绳子,
上面有13个等距的结,把这根绳子分成等长的12段.如图所示,拉紧绳子,构成一个三角形。大家可以发现什么?
A
C
B
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
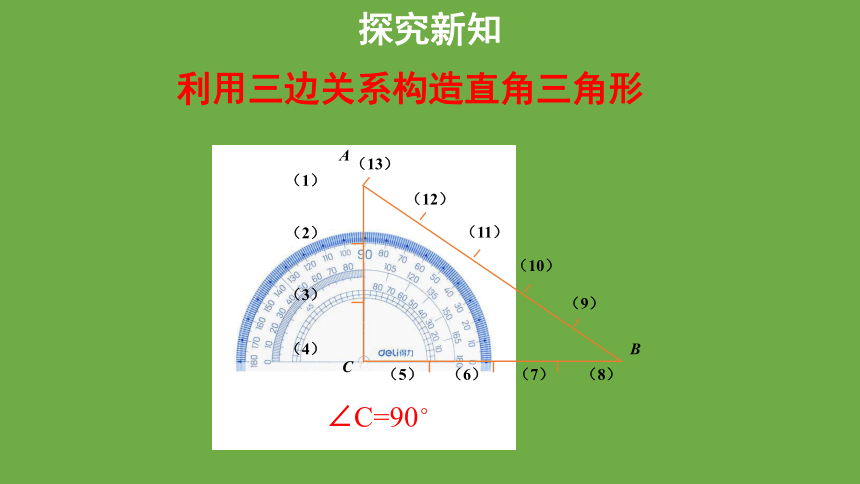
利用三边关系构造直角三角形
探究新知
利用三边关系构造直角三角形
A
C
B
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
∠C=90°
第(1)个结到第(4)个结是3个单位长度即b=3;同理a=4,c=5.
因为32+42=52,
即a2+b2=c2
是否三角形的三边满足a2+b2=c2,我们就可以得到一个直角三角形呢?不妨再找几组数试一试.
A
C
B
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
b
a
c
探究新知
探究新知
活动2:下面四组数分别是一个三角形的三边a,b,c的长:
(1)5,12,13; (2)7,24,25;
(3)8,15,17; (4)5,6,7.
【问题1】 这四组数都满足a2+b2=c2吗
【问题2】 分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
探究新知
问题1
(1)52+122=169=132;
(2) 72+242=625=252;
(3) 82+152=289=172;
(4) 52+62=61≠72.
是直角三角形
是直角三角形
是直角三角形
不是直角三角形
探究新知
归纳总结
(1)判定直角三角形的条件:
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数.
(2)常见的勾股数有:①3,4,5;②9,40,41;③8,15,17;④7,24,25;⑤5,12,13;⑥9,12,15.
(3)勾股数有无数组,一组勾股数中,各数的相同整数倍得到一组新的勾股数.
探究新知
常见的勾股数
典型例题
例 1.一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边的尺寸,那么这个零件符合要求吗?
3
4
5
12
13
B
A
C
D
解: 在△ABD中,AB2+AD2=9+16=25=BD2,
所以△ABD是直角三角形,∠A是直角.
在△BCD中,BD2+BC2=25+144=169=132=CD2,
所以△BCD是直角三角形,∠DBC是直角.
因此这个零件符合要求.
3
4
5
12
13
B
A
C
D
典型例题
典型例题
例2.下列几组数能否作为直角三角形的三边长?请说说你的理由.
(1)9,12,15;(2)15,36,39;
(3)12,35,36;(4)12,18,32.
典型例题
解:根据直角三角形的判定条件进行判断.
(1)92+122=152;(2)152+362=392,
所以(1)(2)两组数可以作为直角三角形的三边;
但(3)122+352≠362,(4)122+182≠322,
所以(3)(4)两组数不能作为直角三角形的三边.
典型例题
例3 ①7,24,25;②8,15,19;③0.6,0.8,1.0;④3n,4n,5n(n>1,且为自然数).上面各组数中,勾股数有( )组.
A.1 B.2 C.3 D.4
例4 (1)下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3 B.a=7,b=24,c=25
C.a=6,b =8,c=10 D.a=3,b=4,c=5
B
A
典型例题
(2)如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形 B. 锐角三角形
C.钝角三角形 D. 以上答案都不对
(3)如图,正方形ABCD是由9个边长为1的
小正方形组成,每个小正方形的顶点都叫
格点,连接AE,AF,则∠EAF=( )
A.30° B. 45° C. 60° D. 35°
A
B
随堂练习
1.如图是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8 m,AD=BC=6 m,AC=9 m,请你帮他看一下,挖的地基是否合格?
随堂练习
解:∵AD2+DC2=62+82=100,AC2=92=81,
∴AD2+DC2≠AC2.
∴△ADC不是直角三角形,∠ADC≠90°.
又∵按标准应为长方形,
四个角应为直角,
∴该农民挖的地基不合格.
D
C
B
A
解:∵AD2+BD2=122+52=132=AB2,
∴由勾股定理的逆定理知△ADB为直角三角形.
∴AD⊥BC.
在Rt△ADC中,由勾股定理,得
DC2=AC2-AD2=152-122=92.
∴DC=9.
D
C
B
A
随堂练习
2.如图,在△ABC中,D为BC边上的点,已知:AB=13,AD=12,AC=15,BD=5,求DC.
随堂练习
3.如图,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积.
解:连接BD,
在△ABD中,∠A是直角,AB=3,AD=4,
∴BD = = =5,
△BCD中,BC=12,DC=13,DB=5,
52+122=132,即BC2+BD2=DC2,∴△BCD是直角三角形,
∴S四边形ABCD=S△ABD+S△BDC= AD AB+ BD BC= ×( 4×3 +5×12) =36.
课堂小结
谈谈本节课的收获:
1.判定直角三角形的方法:如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股数:满足a2+b2=c2的三个正整数,称为勾股数
2.勾股数扩大相同倍数后,仍为勾股数
再见
第一章探索勾股定理
1.2一定是直角三角形吗
学习目标
1.掌握直角三角形的判别条件,掌握常见的勾股数.
2.经历直角三角形的判别条件的探索过程,并能进行简单的应用.
复习回顾
直角三角形有哪些性质?
①有一个内角为直角;
②两个锐角互余;
③两条直角边的平方和等于斜边的平方.
复习回顾
【问题】
一个三角形,满足什么条件时是直角三角形呢?
探究新知
拿出事先准备好的绳子,
上面有13个等距的结,把这根绳子分成等长的12段.如图所示,拉紧绳子,构成一个三角形。大家可以发现什么?
A
C
B
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
利用三边关系构造直角三角形
探究新知
利用三边关系构造直角三角形
A
C
B
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
∠C=90°
第(1)个结到第(4)个结是3个单位长度即b=3;同理a=4,c=5.
因为32+42=52,
即a2+b2=c2
是否三角形的三边满足a2+b2=c2,我们就可以得到一个直角三角形呢?不妨再找几组数试一试.
A
C
B
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
b
a
c
探究新知
探究新知
活动2:下面四组数分别是一个三角形的三边a,b,c的长:
(1)5,12,13; (2)7,24,25;
(3)8,15,17; (4)5,6,7.
【问题1】 这四组数都满足a2+b2=c2吗
【问题2】 分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
探究新知
问题1
(1)52+122=169=132;
(2) 72+242=625=252;
(3) 82+152=289=172;
(4) 52+62=61≠72.
是直角三角形
是直角三角形
是直角三角形
不是直角三角形
探究新知
归纳总结
(1)判定直角三角形的条件:
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数.
(2)常见的勾股数有:①3,4,5;②9,40,41;③8,15,17;④7,24,25;⑤5,12,13;⑥9,12,15.
(3)勾股数有无数组,一组勾股数中,各数的相同整数倍得到一组新的勾股数.
探究新知
常见的勾股数
典型例题
例 1.一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边的尺寸,那么这个零件符合要求吗?
3
4
5
12
13
B
A
C
D
解: 在△ABD中,AB2+AD2=9+16=25=BD2,
所以△ABD是直角三角形,∠A是直角.
在△BCD中,BD2+BC2=25+144=169=132=CD2,
所以△BCD是直角三角形,∠DBC是直角.
因此这个零件符合要求.
3
4
5
12
13
B
A
C
D
典型例题
典型例题
例2.下列几组数能否作为直角三角形的三边长?请说说你的理由.
(1)9,12,15;(2)15,36,39;
(3)12,35,36;(4)12,18,32.
典型例题
解:根据直角三角形的判定条件进行判断.
(1)92+122=152;(2)152+362=392,
所以(1)(2)两组数可以作为直角三角形的三边;
但(3)122+352≠362,(4)122+182≠322,
所以(3)(4)两组数不能作为直角三角形的三边.
典型例题
例3 ①7,24,25;②8,15,19;③0.6,0.8,1.0;④3n,4n,5n(n>1,且为自然数).上面各组数中,勾股数有( )组.
A.1 B.2 C.3 D.4
例4 (1)下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3 B.a=7,b=24,c=25
C.a=6,b =8,c=10 D.a=3,b=4,c=5
B
A
典型例题
(2)如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形 B. 锐角三角形
C.钝角三角形 D. 以上答案都不对
(3)如图,正方形ABCD是由9个边长为1的
小正方形组成,每个小正方形的顶点都叫
格点,连接AE,AF,则∠EAF=( )
A.30° B. 45° C. 60° D. 35°
A
B
随堂练习
1.如图是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8 m,AD=BC=6 m,AC=9 m,请你帮他看一下,挖的地基是否合格?
随堂练习
解:∵AD2+DC2=62+82=100,AC2=92=81,
∴AD2+DC2≠AC2.
∴△ADC不是直角三角形,∠ADC≠90°.
又∵按标准应为长方形,
四个角应为直角,
∴该农民挖的地基不合格.
D
C
B
A
解:∵AD2+BD2=122+52=132=AB2,
∴由勾股定理的逆定理知△ADB为直角三角形.
∴AD⊥BC.
在Rt△ADC中,由勾股定理,得
DC2=AC2-AD2=152-122=92.
∴DC=9.
D
C
B
A
随堂练习
2.如图,在△ABC中,D为BC边上的点,已知:AB=13,AD=12,AC=15,BD=5,求DC.
随堂练习
3.如图,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积.
解:连接BD,
在△ABD中,∠A是直角,AB=3,AD=4,
∴BD = = =5,
△BCD中,BC=12,DC=13,DB=5,
52+122=132,即BC2+BD2=DC2,∴△BCD是直角三角形,
∴S四边形ABCD=S△ABD+S△BDC= AD AB+ BD BC= ×( 4×3 +5×12) =36.
课堂小结
谈谈本节课的收获:
1.判定直角三角形的方法:如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股数:满足a2+b2=c2的三个正整数,称为勾股数
2.勾股数扩大相同倍数后,仍为勾股数
再见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
