2022--2023学年北师大版数学八年级上册第一章勾股定理 自主预习试题(无答案)
文档属性
| 名称 | 2022--2023学年北师大版数学八年级上册第一章勾股定理 自主预习试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 12:49:17 | ||
图片预览


文档简介
第一章勾股定理--自主预习试题
一、单选题
1.在直角三角形中,若两条直角边的长分别是1cm、2cm,则斜边的长为( )cm.
A.3 B. C.2或 D. 或
2.下列条件不能判断三角形是直角三角形的是( )
A.三个内角的比为3:4:5 B.三个内角的比为1:2:3
C.三边的比为3:4:5 D.三边的比为7:24:25
3.以下面各组线段为边,不能构成三角形的是( )
A.5,6,7 B.6,6,6 C.8,4,4 D.20,30,36
4.如图,在 中, , ,分别以顶点 、 为圆心,大于 的长为半径作圆弧,两条圆弧交于点 、 作直线 交边 于点 .若 , ,则 的长是( )
A.10 B.8 C.12 D.
5.如图是某地一的长方形大理石广场示意图,如果小琴要从A角走到C角,至少走( )米
A.90 B.100 C.120 D.140
6.一个直角三角形的三边分别是6cm、8cm、Xcm,则X=( )cm
A.100cm B.10cm
C.10cm 或 cm D.100cm 或28cm
7.中,,高,则BC的长为( )
A.14 B.14或4 C.4 D.无法确定
8.如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米.
A.80 B.50 C.100 D.100
9.已知△ABC的三边分别是6,8,10,则△ABC斜边上的高是( )
A.2 B.2.4 C.4 D.4.8
10.如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
11.如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB= .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
A.6 B.8 C.10 D.12
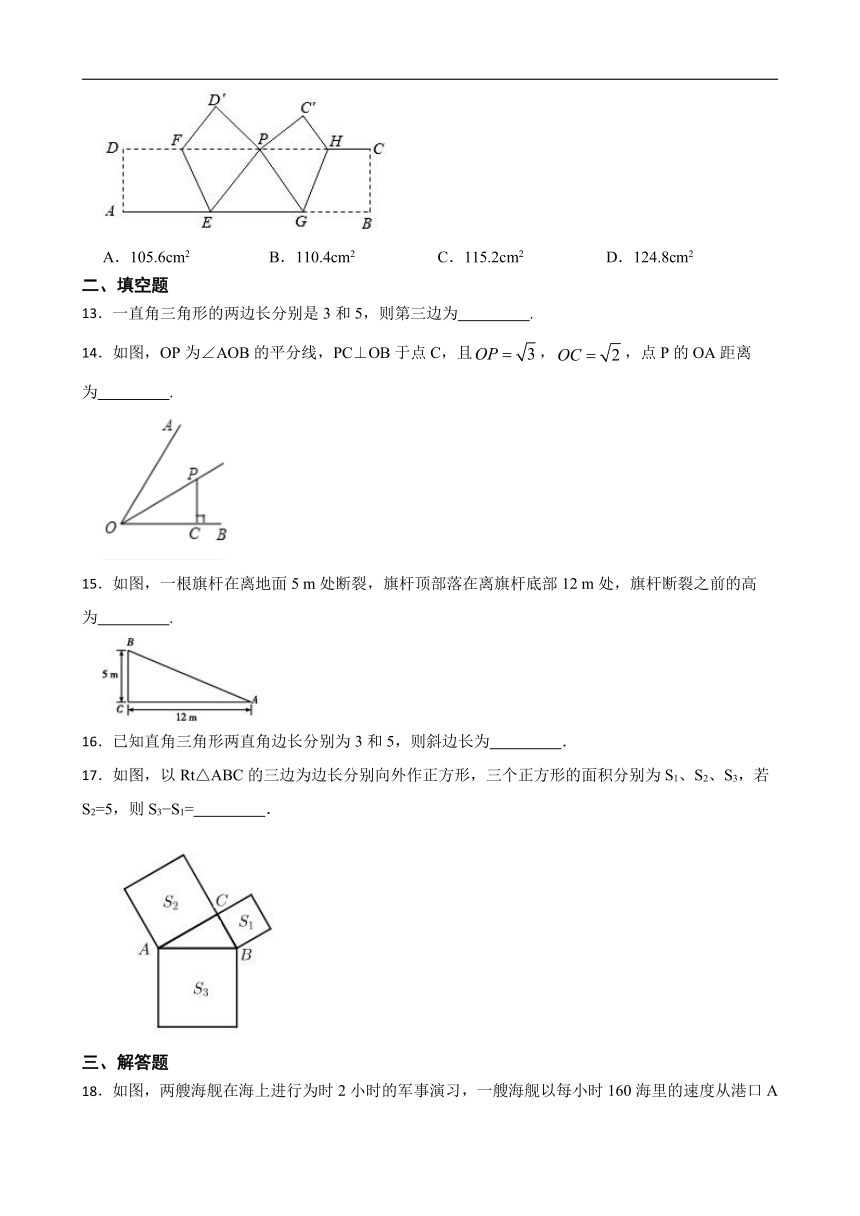
12.如图,ABCD是一张长方形纸片,将AD,BC折起,使A、B两点重合于CD边上的P点,然后压平得折痕EF与GH.若PE=8cm,PG=6cm,EG=10cm,则长方形纸片ABCD的面积为( )
A.105.6cm2 B.110.4cm2 C.115.2cm2 D.124.8cm2
二、填空题
13.一直角三角形的两边长分别是3和5,则第三边为 .
14.如图,OP为∠AOB的平分线,PC⊥OB于点C,且,,点P的OA距离为 .
15.如图,一根旗杆在离地面5 m处断裂,旗杆顶部落在离旗杆底部12 m处,旗杆断裂之前的高为 .
16.已知直角三角形两直角边长分别为3和5,则斜边长为 .
17.如图,以Rt△ABC的三边为边长分别向外作正方形,三个正方形的面积分别为S1、S2、S3,若S2=5,则S3 S1= .
三、解答题
18.如图,两艘海舰在海上进行为时2小时的军事演习,一艘海舰以每小时160海里的速度从港口A出发,向北偏东60°方向航行到达B,另一艘海舰以每小时120海里的速度同时从港口A出发,向南偏东30°方向航行到达C,则此时两艘海舰相距多少海里?
19.如图,△ABC中,AB=AC,BC=4cm,作AD⊥BC,垂足为D,若AD=4cm,求AB的长.
20.在△ABC中,a,b,c是∠A,∠B,∠C的对边,a= ,b= ,c=2,△ABC是否为直角三角形?如果是直角三角形,请指出哪个角是直角.
21.如图,四边形 中, , , , , ,求证: .
22.一个25米长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24米,如果梯子的顶端A沿墙下滑4米,那么梯子底端B也外移4米,对吗?为什么?
23.长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?
一、单选题
1.在直角三角形中,若两条直角边的长分别是1cm、2cm,则斜边的长为( )cm.
A.3 B. C.2或 D. 或
2.下列条件不能判断三角形是直角三角形的是( )
A.三个内角的比为3:4:5 B.三个内角的比为1:2:3
C.三边的比为3:4:5 D.三边的比为7:24:25
3.以下面各组线段为边,不能构成三角形的是( )
A.5,6,7 B.6,6,6 C.8,4,4 D.20,30,36
4.如图,在 中, , ,分别以顶点 、 为圆心,大于 的长为半径作圆弧,两条圆弧交于点 、 作直线 交边 于点 .若 , ,则 的长是( )
A.10 B.8 C.12 D.
5.如图是某地一的长方形大理石广场示意图,如果小琴要从A角走到C角,至少走( )米
A.90 B.100 C.120 D.140
6.一个直角三角形的三边分别是6cm、8cm、Xcm,则X=( )cm
A.100cm B.10cm
C.10cm 或 cm D.100cm 或28cm
7.中,,高,则BC的长为( )
A.14 B.14或4 C.4 D.无法确定
8.如图,A在O正北方向,B在O正东方向,且A、B到点O的距离相等,甲从A出发,以每小时60千米的速度朝正东方向行驶,乙从B出发,以每小时40千米的速度朝正北方向行驶,1小时后,位于点O处的观察员发现甲乙两人之间的夹角为45°,此时甲乙两人相距( )千米.
A.80 B.50 C.100 D.100
9.已知△ABC的三边分别是6,8,10,则△ABC斜边上的高是( )
A.2 B.2.4 C.4 D.4.8
10.如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
11.如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB= .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
A.6 B.8 C.10 D.12
12.如图,ABCD是一张长方形纸片,将AD,BC折起,使A、B两点重合于CD边上的P点,然后压平得折痕EF与GH.若PE=8cm,PG=6cm,EG=10cm,则长方形纸片ABCD的面积为( )
A.105.6cm2 B.110.4cm2 C.115.2cm2 D.124.8cm2
二、填空题
13.一直角三角形的两边长分别是3和5,则第三边为 .
14.如图,OP为∠AOB的平分线,PC⊥OB于点C,且,,点P的OA距离为 .
15.如图,一根旗杆在离地面5 m处断裂,旗杆顶部落在离旗杆底部12 m处,旗杆断裂之前的高为 .
16.已知直角三角形两直角边长分别为3和5,则斜边长为 .
17.如图,以Rt△ABC的三边为边长分别向外作正方形,三个正方形的面积分别为S1、S2、S3,若S2=5,则S3 S1= .
三、解答题
18.如图,两艘海舰在海上进行为时2小时的军事演习,一艘海舰以每小时160海里的速度从港口A出发,向北偏东60°方向航行到达B,另一艘海舰以每小时120海里的速度同时从港口A出发,向南偏东30°方向航行到达C,则此时两艘海舰相距多少海里?
19.如图,△ABC中,AB=AC,BC=4cm,作AD⊥BC,垂足为D,若AD=4cm,求AB的长.
20.在△ABC中,a,b,c是∠A,∠B,∠C的对边,a= ,b= ,c=2,△ABC是否为直角三角形?如果是直角三角形,请指出哪个角是直角.
21.如图,四边形 中, , , , , ,求证: .
22.一个25米长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24米,如果梯子的顶端A沿墙下滑4米,那么梯子底端B也外移4米,对吗?为什么?
23.长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
