2014-2015学年九年级上学期月考数学试卷
文档属性
| 名称 | 2014-2015学年九年级上学期月考数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 289.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-28 19:42:43 | ||
图片预览



文档简介
2014-2015学年九年级(上)月考数学
试卷(10月份)
一、选择题(本题满分24分,共有8道小题,每小题3分,下列每小题都给出标号为A、B、C、D的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.)2·1·c·n·j·y
1.(3分)已知三角形两边长分别为2和9,第三边的长为二次方程x2﹣14x+48=0的根,则这个三角形的周长为( )【来源:21·世纪·教育·网】
A.
11
B.
17
C.
17或19
D.
19
2.(3分)下列方程中,关于x的一元二次方程的是( )
A.
ax2+bx+c=0
B.
3(x﹣1)2=2(x+1)
C.
D.
x2+3x=x2﹣1
3.(3分)元旦期间,一个小组有若干人,他们之间互送贺卡一张,已知全组共送贺卡132张,则这个小组共有( )21教育网
A.
11人
B.
12人
C.
13人
D.
14人
4.(3分)顺次连接某个四边形各边中点得到一个正方形,则原四边形一定是( )
A.
正方形
B.
对角线互相垂直的等腰梯形
C.
菱形
D.
对角线互相垂直且相等的四边形
5.(3分)正方形具有而菱形不具有的性质是( )
A.
对角线互相平分
B.
对角线相等
C.
对角线平分一组对角
D.
对角线互相垂直
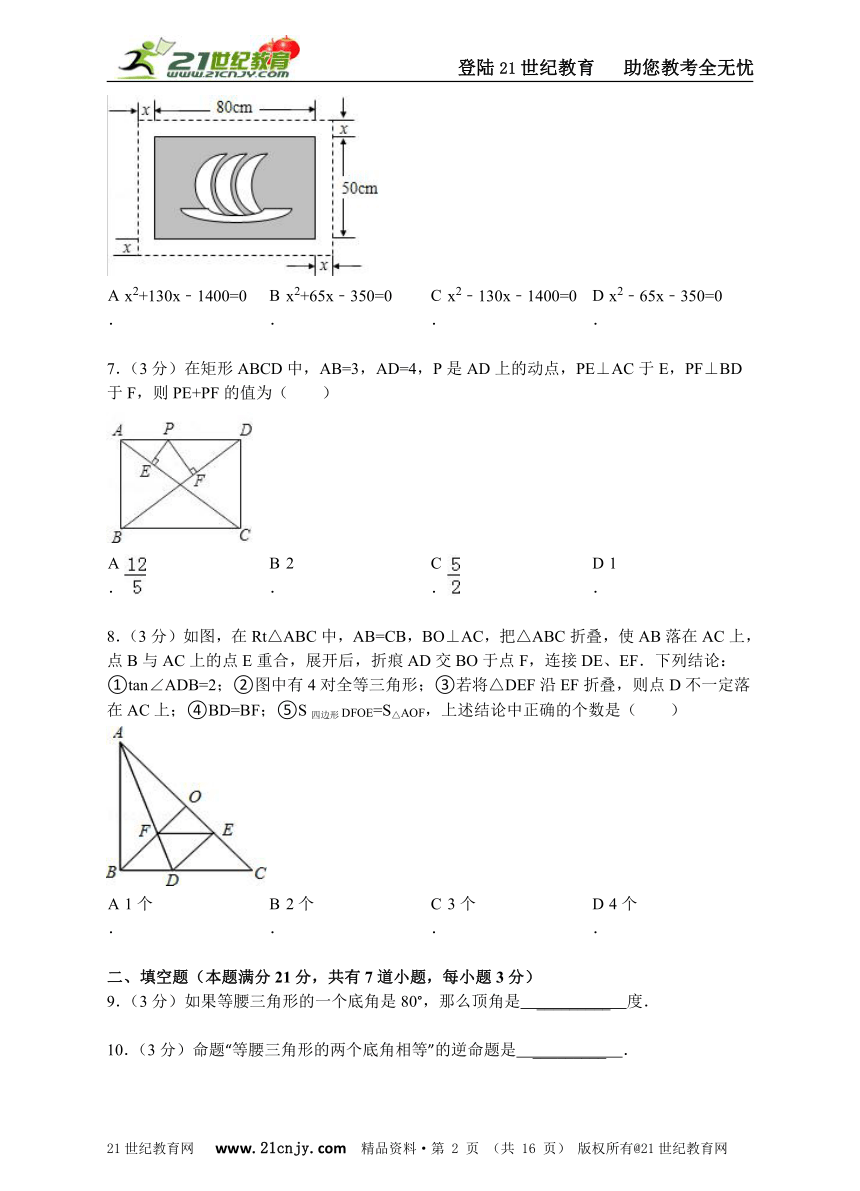
6.(3分)在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为x cm,那么x满足的方程是( )www-2-1-cnjy-com
A.
x2+130x﹣1400=0
B.
x2+65x﹣350=0
C.
x2﹣130x﹣1400=0
D.
x2﹣65x﹣350=0
7.(3分)在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )2-1-c-n-j-y
A.
B.
2
C.
D.
1
8.(3分)如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题(本题满分21分,共有7道小题,每小题3分)
9.(3分)如果等腰三角形的一个底角是80°,那么顶角是 _________ 度.
10.(3分)命题“等腰三角形的两个底角相等”的逆命题是 _________ .
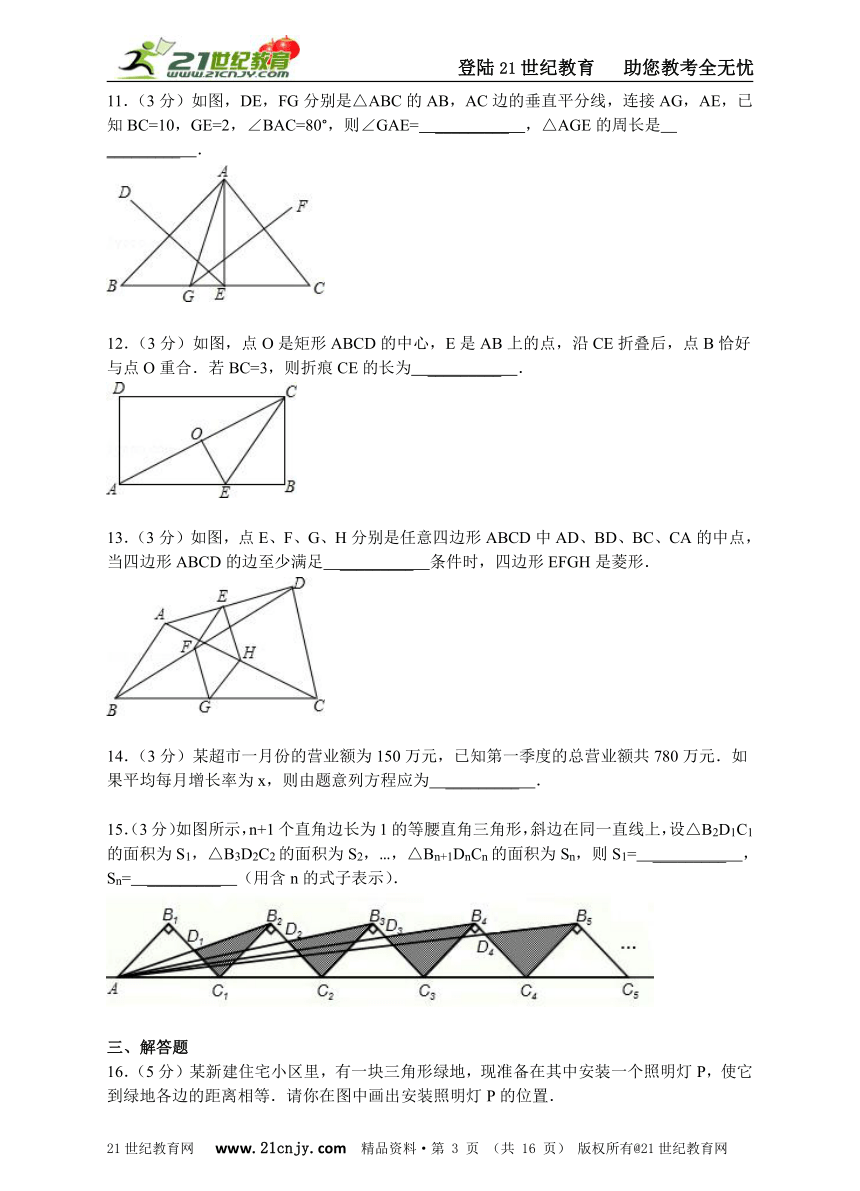
11.(3分)如图,DE,FG分别是△ABC的AB,AC边的垂直平分线,连接AG,AE,已知BC=10,GE=2,∠BAC=80°,则∠GAE= _________ ,△AGE的周长是 _________ . 21*cnjy*com
12.(3分)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合.若BC=3,则折痕CE的长为 _________ .【来源:21cnj*y.co*m】
13.(3分)如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足 _________ 条件时,四边形EFGH是菱形.
14.(3分)某超市一月份的营业额为150万元,已知第一季度的总营业额共780万元.如果平均每月增长率为x,则由题意列方程应为 _________ .【出处:21教育名师】
15.(3分)如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S1= _________ ,Sn= _________ (用含n的式子表示).
三、解答题
16.(5分)某新建住宅小区里,有一块三角形绿地,现准备在其中安装一个照明灯P,使它到绿地各边的距离相等.请你在图中画出安装照明灯P的位置.21教育名师原创作品
17.(10分)解方程
(1)3x2﹣6x﹣1=0(配方法)
(2)3x2=5(2x+1)(公式法)
18.(8分)如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,求:鸡场的长和宽各为多少米?
19.(10分)某超市经销一种成本为40元/kg的水产品,市场调查发现,按50元/kg销售,一个月能售出500kg,销售单位每涨0.1元,月销售量就减少1kg,针对这种水产品的销售情况,超市在月成本不超过10000元的情况下,使得月销售利润达到8000元,请你帮忙算算,销售单价定为多少?
20.(6分)如图,△ABC中,AB=AC,在AB上取一点E,在AC的延长线上取一点F,使CF=BE,连接EF,交BC于点D.求证:DE=DF.
21.(10分)如图,在?ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P.21·世纪*教育网
(1)求证:△ABE≌△DCF;
(2)当∠P满足什么条件时,四边形BECF是菱形?证明你的结论.
22.(14分)【探究发现】
按图1、图2、图3中方式将大小不同的两个正方形放在一起,分别求出阴影部分(△ACF)的面积.(单位:厘米,阴影部分的面积依次用S1、S2、S3表示)【版权所有:21教育】
(1)S1= _________ cm2;S2= _________ cm2;S3= _________ cm2.
(2)归纳总结你的发现: _________
【推理反思】
按图4中方式将大小不同的两个正方形放在一起,设小正方形的边长是bcm,大正方形的边长是acm,求:阴影部分(△ACF)的面积.21*cnjy*com
【应用拓展】
(1)按图4方式将大小不同的两个正方形放在一起,若大正方形的面积是80cm2,则图中阴影三角形的面积是 _________ cm2.
(2)如图5,C是线段AB上任意一点,分别以AC、BC为边在线段AB同侧构造等边三角形△ACD和等边三角形△CBE,若△CBE的边长是1cm,则图中阴影三角形的面积是 _________ cm2.
(3)如图6,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是 _________ .
23.(12分)如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
参考答案与试题解析
3. 解:设这个小组有x人,则每人应送出x﹣1张贺卡,由题意得:
x(x﹣1)=132,
即:x2﹣x﹣132=0,
解得:x1=12,x2=﹣11(不符合题意舍去)
即:这个小组有12人,
故选:B.
4. 解:根据三角形中位线定理,顺次连接某个四边形各边中点得到一个平行四边形,它的一组邻边分别平行且等于四边形对角线的一半.因为正方形四边相等,邻边垂直,所以原四边形的对角线相等且互相垂直.
故选:D.
5. 解:正方形和菱形都满足:四条边都相等,对角线平分一组对角,对角线垂直且互相平分;
菱形的对角线不一定相等,而正方形的对角线一定相等.
故选B.
6. 解:依题意得:(80+2x)(50+2x)=5400,
即4000+260x+4x2=5400,
化简为:4x2+260x﹣1400=0,
即x2+65x﹣350=0.
故选:B.
7. 解:设AP=x,PD=4﹣x.
∵∠EAP=∠EAP,∠AEP=∠ADC;
∴△AEP∽△ADC,故=①;
同理可得△DFP∽△DAB,故=②.
①+②得=,
∴PE+PF=.故选A.
8. 解:①由折叠可得BD=DE,而DC>DE,∴DC>BD,∴tan∠ADB≠2,故①错误;
②图中的全等三角形有△ABF≌△AEF,△ABD≌△AED,△FBD≌△FED,(由折叠可知)
∵OB⊥AC,∴∠AOB=∠COB=90°,
在Rt△AOB和Rt△COB中,
,
∴Rt△AOB≌Rt△COB(HL),
则全等三角形共有4对,故②正确;
③∵AB=CB,BO⊥AC,把△ABC折叠,
∴∠ABO=∠CBO=45°,∠FBD=∠DEF,
∴∠AEF=∠DEF=45°,∴将△DEF沿EF折叠,可得点D一定在AC上,故③错误;
④∵OB⊥AC,且AB=CB,
∴BO为∠ABC的平分线,即∠ABO=∠OBC=45°,
由折叠可知,AD是∠BAC的平分线,即∠BAF=22.5°,
又∵∠BFD为三角形ABF的外角,
∴∠BFD=∠ABO+∠BAF=67.5°,
易得∠BDF=180°﹣45°﹣67.5°=67.5°,
∴∠BFD=∠BDF,
∴BD=BF,故④正确;
⑤连接CF,∵△AOF和△COF等底同高,
∴S△AOF=S△COF,
∵∠AEF=∠ACD=45°,
∴EF∥CD,
∴S△EFD=S△EFC,
∴S四边形DFOE=S△COF,
∴S四边形DFOE=S△AOF,
故⑤正确;
正确的有3个,
故选C.
9. 解:∵三角形是等腰三角形,
∴两个底角相等,
∵等腰三角形的一个底角是80°,
∴另一个底角也是80°,
∴顶角的度数为180°﹣80°﹣80°=20°.
故填20.
11. 解:∵∠BAC=80°,
∴∠B+∠C=180°﹣80°=100°,
∵DE,FG分别是△ABC的AB,AC边的垂直平分线,
∴AE=BE,CG=AG,
∵BC=10,GE=2,
∴AE+AG=BE+CG=10+2=12,
∴△AGE的周长是AG+AE+EG=12+2=14,
∵AE=BE,CG=AG,
∴∠B=∠EAB,∠C=∠GAC,
∴∠EAB+∠GAC=∠BAC+∠GAE=100°,
∴∠GAE=100°﹣80°=20°,
故答案为:20°,14.
12. 解:∵△CEO是△CEB翻折而成,
∴BC=OC,BE=OE,
∵O是矩形ABCD的中心,
∴OE是AC的垂直平分线,AC=2BC=2×3=6,
∴AE=CE,
在Rt△ABC中,AC2=AB2+BC2,
即62=AB2+32,
解得AB=3,
在Rt△AOE中,设OE=x,则AE=3﹣x,
AE2=AO2+OE2,
即(3﹣x)2=32+x2,
解得x=,
∴AE=EC=3﹣=2.
故答案为:2.
13. 解:需添加条件AB=CD.
∵E,F是AD,DB中点,
∴EF∥AB,EF=AB,
∵H,G是AC,BC中点,
∴HG∥AB,HG=AB,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形,
∵E,H是AD,AC中点,
∴EH=CD,
∵AB=CD,
∴EF=EH,
∴四边形EFGH是菱形.
故答案为:AB=CD.
14. 解:∵一月份的营业额为150万元,平均每月增长率为x,
∴二月份的营业额为150×(1+x),
∴三月份的营业额为150×(1+x)×(1+x)=150×(1+x)2,
∴可列方程为150+1050×(1+x)+100×(1+x)2=780,
即150[1+(1+x)+(1+x)2]=780.
故答案为:150[1+(1+x)+(1+x)2]=780.
15. 解:∵n+1个边长为1的等腰三角形有一条边在同一直线上,
∴S△AB1C1=×1×1=,
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=1,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=×=,
故答案为:;
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=×=,
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,
∴S3=×=,
∴S4=×=,
…
∴Sn=
故答案为:.
16. 解:如图所示:
点P就是安装照明灯的位置.
17. 解:(1)解:移项得:3x2﹣6x=1,
x2﹣2x=,
配方得:x2﹣2x+1=+1,
(x﹣1)2=,
x﹣1=±,
x1=1+,x2=1﹣.
(2)整理得:3x2﹣10x﹣5=0,
b2﹣4ac=(﹣10)2﹣4×3×(﹣5)=160,
x=,
x1=,x2=.
18. 解:设鸡场的长为x,因为篱笆总长为33米,由图可知宽为:米,
则根据题意列方程为:
x×=150,
解得:x1=15,x2=20(大于墙长,舍去).
宽为:10米.
所以鸡场的长为15米,宽为10米.
19. 解:设销售单价定为x元,根据题意得:
(x﹣40)[500﹣(x﹣50)÷0.1]=8000.
解得:x1=60,x2=80
当售价为60时,月成本[500﹣(60﹣50)÷0.1]×40=16000>10000,所以舍去.
当售价为80时,月成本[500﹣(80﹣50)÷0.1]×40=8000<10000.
答:销售单价定为80元.
20. 解:作EG∥AC交BC于G,
∴∠BGE=∠ACB,∠GED=∠F,∠EGD=∠FCD.
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠BGE,
∴BE=EG.
∵CF=BE,
∴CF=GE.
在△GED和△CFD中,
,
∴△GED≌△CFD(ASA),
∴DE=DF.
21(1)证明:在?ABDC中,∠BAC=∠D,AB=CD,AC=BD,
∵E、F分别是AC、BD的中点,
∴AE=DF,
在△ABE和△DCF中,,
∴△ABE≌△DCF(SAS);
(2)解:∠P=90°时,四边形BECF是菱形.理由如下:
在?ABCD中,AB∥CD,
∵AP∥BC,
∴四边形ABCP是平行四边形,
∴∠ABC=∠P=90°,
∵E是AC的中点,
∴BE=CE=AC,
∵E、F分别是AC、BD的中点,
∴BF=CE,
又∵AC∥BD,
∴四边形BECF是平行四边形,
∴四边形BECF是菱形(邻边相等的平行四边形是菱形).
22. 解:【探究发现】
(1)S1=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×2×(10﹣2)+2×2+×10×10﹣×2×(2+10)=8+4+50﹣12=50(cm2);21世纪教育网版权所有
S2=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×4×(10﹣4)+4×4+×10×10﹣×4×(4+10)=12+16+50﹣28=50(cm2);21cnjy.com
S3=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×8×(10﹣8)+8×8+×10×10﹣×8×(8+10)=8+64+50﹣72=50(cm2);21·cn·jy·com
(2)归纳总结得S△ACF=S正方形ABCD.
【推理反思】
S△ACF=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×b×(a﹣b)+b×b+×a×a﹣×b×(b+a)=ab﹣b2+b2+a2﹣b2﹣ab=a2;www.21-cn-jy.com
【应用拓展】
(1)由推理反思得S△ACF=S正方形ABCD=×80cm2=40cm2;
(2)∵△ACD和△BCE都是等边三角形,
∴∠ACD=60°,∠CBE=60°,
∴∠ACD=∠CBE,
∴CD∥BE,
∴S△DEB=S△CBE=×1×=cm2.
(3)如图,设BF交CE于点H,
∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴=,
即=,
解得:CH=,
所以,DH=CD﹣CH=2﹣=,
∵∠A=120°,
∴∠ECG=∠ABC=180°﹣120°=60°,
∴点B到CD的距离为2×=,
点G到CE的距离为3×=,
∴阴影部分的面积=S△BDH+S△FDH
=××+××
=.
23. 解:∵AB=10cm,AC=8cm,BC=6cm,
∴由勾股定理逆定理得△ABC为直角三角形,∠C为直角.
(1)BP=2t,则AP=10﹣2t.
∵PQ∥BC,∴,即,解得t=,
∴当t=s时,PQ∥BC.
(2)如答图1所示,过P点作PD⊥AC于点D.
∴PD∥BC,
∴,
即,
解得PD=6﹣t.
S=×AQ×PD=×2t×(6﹣t)
=﹣t2+6t
=﹣(t﹣)2+,
∴当t=s时,S取得最大值,最大值为cm2.
(3)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△AQP=S△ABC,而S△ABC=AC?BC=24,∴此时S△AQP=12.
由(2)可知,S△AQP=﹣t2+6t,
∴﹣t2+6t=12,化简得:t2﹣5t+10=0,
∵△=(﹣5)2﹣4×1×10=﹣15<0,此方程无解,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分.
(4)假设存在时刻t,使四边形AQPQ′为菱形,则有AQ=PQ=BP=2t.
如答图2所示,过P点作PD⊥AC于点D,则有PD∥BC,
∴,即,
解得:PD=6﹣t,AD=8﹣t,
∴QD=AD﹣AQ=8﹣t﹣2t=8﹣t.
在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,
即(8﹣t)2+(6﹣t)2=(2t)2,
化简得:13t2﹣90t+125=0,
解得:t1=5,t2=,
∵t=5s时,AQ=10cm>AC,不符合题意,舍去,∴t=.
由(2)可知,S△AQP=﹣t2+6t,
∴S菱形AQPQ′=2S△AQP=2×(﹣t2+6t)=2×[﹣×()2+6×]=(cm2).
所以存在时刻t,使四边形AQPQ′为菱形,此时菱形的面积为cm2.
试卷(10月份)
一、选择题(本题满分24分,共有8道小题,每小题3分,下列每小题都给出标号为A、B、C、D的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.)2·1·c·n·j·y
1.(3分)已知三角形两边长分别为2和9,第三边的长为二次方程x2﹣14x+48=0的根,则这个三角形的周长为( )【来源:21·世纪·教育·网】
A.
11
B.
17
C.
17或19
D.
19
2.(3分)下列方程中,关于x的一元二次方程的是( )
A.
ax2+bx+c=0
B.
3(x﹣1)2=2(x+1)
C.
D.
x2+3x=x2﹣1
3.(3分)元旦期间,一个小组有若干人,他们之间互送贺卡一张,已知全组共送贺卡132张,则这个小组共有( )21教育网
A.
11人
B.
12人
C.
13人
D.
14人
4.(3分)顺次连接某个四边形各边中点得到一个正方形,则原四边形一定是( )
A.
正方形
B.
对角线互相垂直的等腰梯形
C.
菱形
D.
对角线互相垂直且相等的四边形
5.(3分)正方形具有而菱形不具有的性质是( )
A.
对角线互相平分
B.
对角线相等
C.
对角线平分一组对角
D.
对角线互相垂直
6.(3分)在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为x cm,那么x满足的方程是( )www-2-1-cnjy-com
A.
x2+130x﹣1400=0
B.
x2+65x﹣350=0
C.
x2﹣130x﹣1400=0
D.
x2﹣65x﹣350=0
7.(3分)在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )2-1-c-n-j-y
A.
B.
2
C.
D.
1
8.(3分)如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①tan∠ADB=2;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点D不一定落在AC上;④BD=BF;⑤S四边形DFOE=S△AOF,上述结论中正确的个数是( )
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题(本题满分21分,共有7道小题,每小题3分)
9.(3分)如果等腰三角形的一个底角是80°,那么顶角是 _________ 度.
10.(3分)命题“等腰三角形的两个底角相等”的逆命题是 _________ .
11.(3分)如图,DE,FG分别是△ABC的AB,AC边的垂直平分线,连接AG,AE,已知BC=10,GE=2,∠BAC=80°,则∠GAE= _________ ,△AGE的周长是 _________ . 21*cnjy*com
12.(3分)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合.若BC=3,则折痕CE的长为 _________ .【来源:21cnj*y.co*m】
13.(3分)如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足 _________ 条件时,四边形EFGH是菱形.
14.(3分)某超市一月份的营业额为150万元,已知第一季度的总营业额共780万元.如果平均每月增长率为x,则由题意列方程应为 _________ .【出处:21教育名师】
15.(3分)如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S1= _________ ,Sn= _________ (用含n的式子表示).
三、解答题
16.(5分)某新建住宅小区里,有一块三角形绿地,现准备在其中安装一个照明灯P,使它到绿地各边的距离相等.请你在图中画出安装照明灯P的位置.21教育名师原创作品
17.(10分)解方程
(1)3x2﹣6x﹣1=0(配方法)
(2)3x2=5(2x+1)(公式法)
18.(8分)如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,求:鸡场的长和宽各为多少米?
19.(10分)某超市经销一种成本为40元/kg的水产品,市场调查发现,按50元/kg销售,一个月能售出500kg,销售单位每涨0.1元,月销售量就减少1kg,针对这种水产品的销售情况,超市在月成本不超过10000元的情况下,使得月销售利润达到8000元,请你帮忙算算,销售单价定为多少?
20.(6分)如图,△ABC中,AB=AC,在AB上取一点E,在AC的延长线上取一点F,使CF=BE,连接EF,交BC于点D.求证:DE=DF.
21.(10分)如图,在?ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P.21·世纪*教育网
(1)求证:△ABE≌△DCF;
(2)当∠P满足什么条件时,四边形BECF是菱形?证明你的结论.
22.(14分)【探究发现】
按图1、图2、图3中方式将大小不同的两个正方形放在一起,分别求出阴影部分(△ACF)的面积.(单位:厘米,阴影部分的面积依次用S1、S2、S3表示)【版权所有:21教育】
(1)S1= _________ cm2;S2= _________ cm2;S3= _________ cm2.
(2)归纳总结你的发现: _________
【推理反思】
按图4中方式将大小不同的两个正方形放在一起,设小正方形的边长是bcm,大正方形的边长是acm,求:阴影部分(△ACF)的面积.21*cnjy*com
【应用拓展】
(1)按图4方式将大小不同的两个正方形放在一起,若大正方形的面积是80cm2,则图中阴影三角形的面积是 _________ cm2.
(2)如图5,C是线段AB上任意一点,分别以AC、BC为边在线段AB同侧构造等边三角形△ACD和等边三角形△CBE,若△CBE的边长是1cm,则图中阴影三角形的面积是 _________ cm2.
(3)如图6,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是 _________ .
23.(12分)如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
参考答案与试题解析
3. 解:设这个小组有x人,则每人应送出x﹣1张贺卡,由题意得:
x(x﹣1)=132,
即:x2﹣x﹣132=0,
解得:x1=12,x2=﹣11(不符合题意舍去)
即:这个小组有12人,
故选:B.
4. 解:根据三角形中位线定理,顺次连接某个四边形各边中点得到一个平行四边形,它的一组邻边分别平行且等于四边形对角线的一半.因为正方形四边相等,邻边垂直,所以原四边形的对角线相等且互相垂直.
故选:D.
5. 解:正方形和菱形都满足:四条边都相等,对角线平分一组对角,对角线垂直且互相平分;
菱形的对角线不一定相等,而正方形的对角线一定相等.
故选B.
6. 解:依题意得:(80+2x)(50+2x)=5400,
即4000+260x+4x2=5400,
化简为:4x2+260x﹣1400=0,
即x2+65x﹣350=0.
故选:B.
7. 解:设AP=x,PD=4﹣x.
∵∠EAP=∠EAP,∠AEP=∠ADC;
∴△AEP∽△ADC,故=①;
同理可得△DFP∽△DAB,故=②.
①+②得=,
∴PE+PF=.故选A.
8. 解:①由折叠可得BD=DE,而DC>DE,∴DC>BD,∴tan∠ADB≠2,故①错误;
②图中的全等三角形有△ABF≌△AEF,△ABD≌△AED,△FBD≌△FED,(由折叠可知)
∵OB⊥AC,∴∠AOB=∠COB=90°,
在Rt△AOB和Rt△COB中,
,
∴Rt△AOB≌Rt△COB(HL),
则全等三角形共有4对,故②正确;
③∵AB=CB,BO⊥AC,把△ABC折叠,
∴∠ABO=∠CBO=45°,∠FBD=∠DEF,
∴∠AEF=∠DEF=45°,∴将△DEF沿EF折叠,可得点D一定在AC上,故③错误;
④∵OB⊥AC,且AB=CB,
∴BO为∠ABC的平分线,即∠ABO=∠OBC=45°,
由折叠可知,AD是∠BAC的平分线,即∠BAF=22.5°,
又∵∠BFD为三角形ABF的外角,
∴∠BFD=∠ABO+∠BAF=67.5°,
易得∠BDF=180°﹣45°﹣67.5°=67.5°,
∴∠BFD=∠BDF,
∴BD=BF,故④正确;
⑤连接CF,∵△AOF和△COF等底同高,
∴S△AOF=S△COF,
∵∠AEF=∠ACD=45°,
∴EF∥CD,
∴S△EFD=S△EFC,
∴S四边形DFOE=S△COF,
∴S四边形DFOE=S△AOF,
故⑤正确;
正确的有3个,
故选C.
9. 解:∵三角形是等腰三角形,
∴两个底角相等,
∵等腰三角形的一个底角是80°,
∴另一个底角也是80°,
∴顶角的度数为180°﹣80°﹣80°=20°.
故填20.
11. 解:∵∠BAC=80°,
∴∠B+∠C=180°﹣80°=100°,
∵DE,FG分别是△ABC的AB,AC边的垂直平分线,
∴AE=BE,CG=AG,
∵BC=10,GE=2,
∴AE+AG=BE+CG=10+2=12,
∴△AGE的周长是AG+AE+EG=12+2=14,
∵AE=BE,CG=AG,
∴∠B=∠EAB,∠C=∠GAC,
∴∠EAB+∠GAC=∠BAC+∠GAE=100°,
∴∠GAE=100°﹣80°=20°,
故答案为:20°,14.
12. 解:∵△CEO是△CEB翻折而成,
∴BC=OC,BE=OE,
∵O是矩形ABCD的中心,
∴OE是AC的垂直平分线,AC=2BC=2×3=6,
∴AE=CE,
在Rt△ABC中,AC2=AB2+BC2,
即62=AB2+32,
解得AB=3,
在Rt△AOE中,设OE=x,则AE=3﹣x,
AE2=AO2+OE2,
即(3﹣x)2=32+x2,
解得x=,
∴AE=EC=3﹣=2.
故答案为:2.
13. 解:需添加条件AB=CD.
∵E,F是AD,DB中点,
∴EF∥AB,EF=AB,
∵H,G是AC,BC中点,
∴HG∥AB,HG=AB,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形,
∵E,H是AD,AC中点,
∴EH=CD,
∵AB=CD,
∴EF=EH,
∴四边形EFGH是菱形.
故答案为:AB=CD.
14. 解:∵一月份的营业额为150万元,平均每月增长率为x,
∴二月份的营业额为150×(1+x),
∴三月份的营业额为150×(1+x)×(1+x)=150×(1+x)2,
∴可列方程为150+1050×(1+x)+100×(1+x)2=780,
即150[1+(1+x)+(1+x)2]=780.
故答案为:150[1+(1+x)+(1+x)2]=780.
15. 解:∵n+1个边长为1的等腰三角形有一条边在同一直线上,
∴S△AB1C1=×1×1=,
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=1,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=×=,
故答案为:;
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=×=,
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,
∴S3=×=,
∴S4=×=,
…
∴Sn=
故答案为:.
16. 解:如图所示:
点P就是安装照明灯的位置.
17. 解:(1)解:移项得:3x2﹣6x=1,
x2﹣2x=,
配方得:x2﹣2x+1=+1,
(x﹣1)2=,
x﹣1=±,
x1=1+,x2=1﹣.
(2)整理得:3x2﹣10x﹣5=0,
b2﹣4ac=(﹣10)2﹣4×3×(﹣5)=160,
x=,
x1=,x2=.
18. 解:设鸡场的长为x,因为篱笆总长为33米,由图可知宽为:米,
则根据题意列方程为:
x×=150,
解得:x1=15,x2=20(大于墙长,舍去).
宽为:10米.
所以鸡场的长为15米,宽为10米.
19. 解:设销售单价定为x元,根据题意得:
(x﹣40)[500﹣(x﹣50)÷0.1]=8000.
解得:x1=60,x2=80
当售价为60时,月成本[500﹣(60﹣50)÷0.1]×40=16000>10000,所以舍去.
当售价为80时,月成本[500﹣(80﹣50)÷0.1]×40=8000<10000.
答:销售单价定为80元.
20. 解:作EG∥AC交BC于G,
∴∠BGE=∠ACB,∠GED=∠F,∠EGD=∠FCD.
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠BGE,
∴BE=EG.
∵CF=BE,
∴CF=GE.
在△GED和△CFD中,
,
∴△GED≌△CFD(ASA),
∴DE=DF.
21(1)证明:在?ABDC中,∠BAC=∠D,AB=CD,AC=BD,
∵E、F分别是AC、BD的中点,
∴AE=DF,
在△ABE和△DCF中,,
∴△ABE≌△DCF(SAS);
(2)解:∠P=90°时,四边形BECF是菱形.理由如下:
在?ABCD中,AB∥CD,
∵AP∥BC,
∴四边形ABCP是平行四边形,
∴∠ABC=∠P=90°,
∵E是AC的中点,
∴BE=CE=AC,
∵E、F分别是AC、BD的中点,
∴BF=CE,
又∵AC∥BD,
∴四边形BECF是平行四边形,
∴四边形BECF是菱形(邻边相等的平行四边形是菱形).
22. 解:【探究发现】
(1)S1=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×2×(10﹣2)+2×2+×10×10﹣×2×(2+10)=8+4+50﹣12=50(cm2);21世纪教育网版权所有
S2=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×4×(10﹣4)+4×4+×10×10﹣×4×(4+10)=12+16+50﹣28=50(cm2);21cnjy.com
S3=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×8×(10﹣8)+8×8+×10×10﹣×8×(8+10)=8+64+50﹣72=50(cm2);21·cn·jy·com
(2)归纳总结得S△ACF=S正方形ABCD.
【推理反思】
S△ACF=S四边形ACEF﹣S△CEF=S△AFG+S正方形DEFG+S△ADC﹣S△CEF=×b×(a﹣b)+b×b+×a×a﹣×b×(b+a)=ab﹣b2+b2+a2﹣b2﹣ab=a2;www.21-cn-jy.com
【应用拓展】
(1)由推理反思得S△ACF=S正方形ABCD=×80cm2=40cm2;
(2)∵△ACD和△BCE都是等边三角形,
∴∠ACD=60°,∠CBE=60°,
∴∠ACD=∠CBE,
∴CD∥BE,
∴S△DEB=S△CBE=×1×=cm2.
(3)如图,设BF交CE于点H,
∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴=,
即=,
解得:CH=,
所以,DH=CD﹣CH=2﹣=,
∵∠A=120°,
∴∠ECG=∠ABC=180°﹣120°=60°,
∴点B到CD的距离为2×=,
点G到CE的距离为3×=,
∴阴影部分的面积=S△BDH+S△FDH
=××+××
=.
23. 解:∵AB=10cm,AC=8cm,BC=6cm,
∴由勾股定理逆定理得△ABC为直角三角形,∠C为直角.
(1)BP=2t,则AP=10﹣2t.
∵PQ∥BC,∴,即,解得t=,
∴当t=s时,PQ∥BC.
(2)如答图1所示,过P点作PD⊥AC于点D.
∴PD∥BC,
∴,
即,
解得PD=6﹣t.
S=×AQ×PD=×2t×(6﹣t)
=﹣t2+6t
=﹣(t﹣)2+,
∴当t=s时,S取得最大值,最大值为cm2.
(3)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△AQP=S△ABC,而S△ABC=AC?BC=24,∴此时S△AQP=12.
由(2)可知,S△AQP=﹣t2+6t,
∴﹣t2+6t=12,化简得:t2﹣5t+10=0,
∵△=(﹣5)2﹣4×1×10=﹣15<0,此方程无解,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分.
(4)假设存在时刻t,使四边形AQPQ′为菱形,则有AQ=PQ=BP=2t.
如答图2所示,过P点作PD⊥AC于点D,则有PD∥BC,
∴,即,
解得:PD=6﹣t,AD=8﹣t,
∴QD=AD﹣AQ=8﹣t﹣2t=8﹣t.
在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,
即(8﹣t)2+(6﹣t)2=(2t)2,
化简得:13t2﹣90t+125=0,
解得:t1=5,t2=,
∵t=5s时,AQ=10cm>AC,不符合题意,舍去,∴t=.
由(2)可知,S△AQP=﹣t2+6t,
∴S菱形AQPQ′=2S△AQP=2×(﹣t2+6t)=2×[﹣×()2+6×]=(cm2).
所以存在时刻t,使四边形AQPQ′为菱形,此时菱形的面积为cm2.
同课章节目录
