21.3.2 几何图形与一元二次方程同步习题精讲课件(预习导航+堂堂清+日日清)
文档属性
| 名称 | 21.3.2 几何图形与一元二次方程同步习题精讲课件(预习导航+堂堂清+日日清) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-28 21:11:12 | ||
图片预览





文档简介
课件13张PPT。21.3 实际问题与一元二次方程第2课时 几何图形与一元二次方程面积问题:求不规则图形的面积问题,往往把不规则图形转化成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程.几何图形的面积问题 1.(3分)一个面积为35 m2的矩形苗圃,它的长比宽多2 m,则这个苗圃的长为( )
A.5 m B.6 m C.7 m D.8 m
2.(3分)一个梯形的面积为160 cm2,上底比高多4 cm,下底比高多20 cm,这个梯形的高为( )
A.8 cm B.20 cm
C.8 cm或20 cm D.以上都不正确CA3.(3分)从一块正方形的木板上锯掉2 m宽的长方形木条,剩下的面积是48 m2,则原来这块木板的面积是( )
A.64 m2 B.100 m2 C.121 m2 D.144 m2
4.(3分)要用一条长为24 cm的铁丝围成一个斜边长是10 cm的直角三角形,则两直角边的长分别为( )
A.5 cm,9 cm B.6 cm,8 cm
C.4 cm,10 cm D.7 cm,7 cmAB5.(4分) 在宽为20米,长为32米的矩形地面上修筑同样宽的道路,余下部分种植草坪.要使草坪的面积为540平方米,则道路的宽为( )
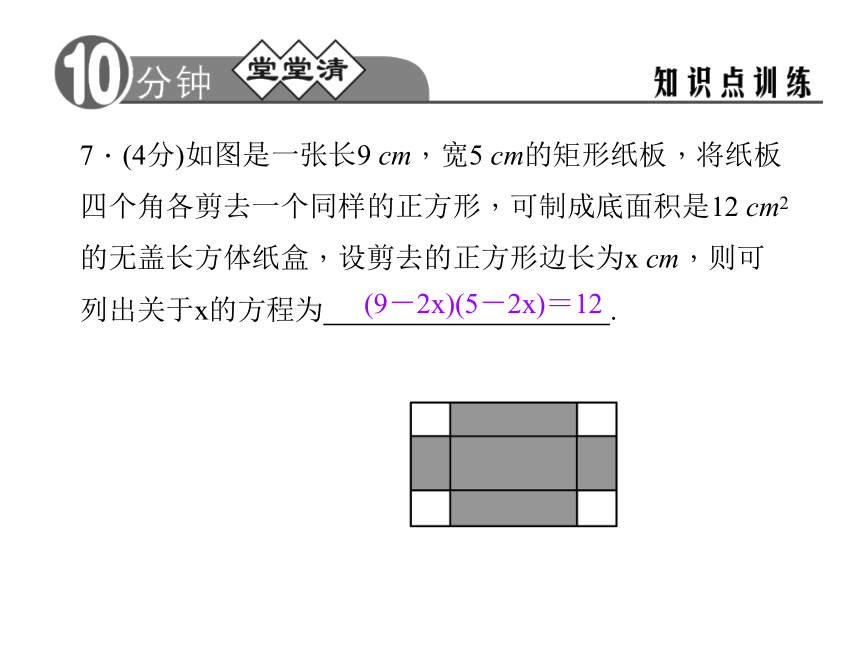
A.5米 B.3米 C.2米 D.2米或5米 C 6.(4分)如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6 m.若矩形的面积为4 m2,则AB的长度是____m.(可利用的围墙长度超过6 m)17.(4分)如图是一张长9 cm,宽5 cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12 cm2的无盖长方体纸盒,设剪去的正方形边长为x cm,则可列出关于x的方程为 .(9-2x)(5-2x)=128.(8分)如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25 m),现在已备足可以砌50 m长的墙的材料,试设计一种砌法,使矩形花园的面积为300 m2.
解:设AB为x m,则BC=(50-2x) m,由题意得x(50-2x)=300,整理得x2-25x+150=0,解得x1=10,x2=15,当x=10时,BC=50-2×10=30>25舍去,当x=15时,BC=50-2×15=20,则当AB为15 m,BC为20 m时,花园的总面积为300 m29.(8分)为响应市委市政府提出的建设“绿色家园”的号召,我市某单位准备将院内一块长30 m,宽20 m的长方形空地,建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532 m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)解:设小道进出口宽度为x米,依题意得(30-2x)(20-x)=532,整理得x2-35x+34=0.解得x1=1,x2=34(不合题意舍去),则小道进出口宽度为1米10.如图,在Rt△ABC中,点P,Q分别同时由A,C两点沿AC方向,CB方向出发,P点运动的速度为每秒1 cm,Q点运动的速度为每秒2 cm,点P运动到C,若点Q运动到B时,两点均停止运动,现已知AC=12 cm,BC=9 cm,设运动了t秒时,△PQC的面积等于△ABC面积的一半,则t的值为( )
A.3秒 B.9秒
C.3秒或9秒 D.4.5秒A11.有一面积为54 m2的长方形,将它的一边剪短5 m,另一边剪短2 m,恰好变成一个正方形,这个正方形的边长是多少?设正方形的边长为x m,请列出你求解的方程: .(x+5)(x+2)=5412.如图,已知点A是一次函数y=x-4在第四象限的图象上的一个动点,且矩形ABOC的面积等于3,则点A的坐标为 .(1,-3)或(3,-1)13.(14分)将一条长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17 cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12 cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.14.(14分)某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2∶1,在温室内,沿前侧内墙保留3 m宽的空地,其他三侧内墙各保留1 m宽的通道,当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288 m2?解:设长为2x m,宽为x m,则(x-2)(2x-4)=288,∴x1=14,x2=-10(舍去),∴长为28 m,宽为14 m15.(14分)在一块长16 m,宽12 m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.(1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗?若不符合,请用方程的方法说明理由;
(2)你还有其他的设计方案吗?请你设计出草图,将花园部分涂上阴影,并加以说明.
A.5 m B.6 m C.7 m D.8 m
2.(3分)一个梯形的面积为160 cm2,上底比高多4 cm,下底比高多20 cm,这个梯形的高为( )
A.8 cm B.20 cm
C.8 cm或20 cm D.以上都不正确CA3.(3分)从一块正方形的木板上锯掉2 m宽的长方形木条,剩下的面积是48 m2,则原来这块木板的面积是( )
A.64 m2 B.100 m2 C.121 m2 D.144 m2
4.(3分)要用一条长为24 cm的铁丝围成一个斜边长是10 cm的直角三角形,则两直角边的长分别为( )
A.5 cm,9 cm B.6 cm,8 cm
C.4 cm,10 cm D.7 cm,7 cmAB5.(4分) 在宽为20米,长为32米的矩形地面上修筑同样宽的道路,余下部分种植草坪.要使草坪的面积为540平方米,则道路的宽为( )
A.5米 B.3米 C.2米 D.2米或5米 C 6.(4分)如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6 m.若矩形的面积为4 m2,则AB的长度是____m.(可利用的围墙长度超过6 m)17.(4分)如图是一张长9 cm,宽5 cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12 cm2的无盖长方体纸盒,设剪去的正方形边长为x cm,则可列出关于x的方程为 .(9-2x)(5-2x)=128.(8分)如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25 m),现在已备足可以砌50 m长的墙的材料,试设计一种砌法,使矩形花园的面积为300 m2.
解:设AB为x m,则BC=(50-2x) m,由题意得x(50-2x)=300,整理得x2-25x+150=0,解得x1=10,x2=15,当x=10时,BC=50-2×10=30>25舍去,当x=15时,BC=50-2×15=20,则当AB为15 m,BC为20 m时,花园的总面积为300 m29.(8分)为响应市委市政府提出的建设“绿色家园”的号召,我市某单位准备将院内一块长30 m,宽20 m的长方形空地,建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532 m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)解:设小道进出口宽度为x米,依题意得(30-2x)(20-x)=532,整理得x2-35x+34=0.解得x1=1,x2=34(不合题意舍去),则小道进出口宽度为1米10.如图,在Rt△ABC中,点P,Q分别同时由A,C两点沿AC方向,CB方向出发,P点运动的速度为每秒1 cm,Q点运动的速度为每秒2 cm,点P运动到C,若点Q运动到B时,两点均停止运动,现已知AC=12 cm,BC=9 cm,设运动了t秒时,△PQC的面积等于△ABC面积的一半,则t的值为( )
A.3秒 B.9秒
C.3秒或9秒 D.4.5秒A11.有一面积为54 m2的长方形,将它的一边剪短5 m,另一边剪短2 m,恰好变成一个正方形,这个正方形的边长是多少?设正方形的边长为x m,请列出你求解的方程: .(x+5)(x+2)=5412.如图,已知点A是一次函数y=x-4在第四象限的图象上的一个动点,且矩形ABOC的面积等于3,则点A的坐标为 .(1,-3)或(3,-1)13.(14分)将一条长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17 cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12 cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.14.(14分)某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2∶1,在温室内,沿前侧内墙保留3 m宽的空地,其他三侧内墙各保留1 m宽的通道,当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288 m2?解:设长为2x m,宽为x m,则(x-2)(2x-4)=288,∴x1=14,x2=-10(舍去),∴长为28 m,宽为14 m15.(14分)在一块长16 m,宽12 m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.(1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗?若不符合,请用方程的方法说明理由;
(2)你还有其他的设计方案吗?请你设计出草图,将花园部分涂上阴影,并加以说明.
同课章节目录
