苏科版八上 第三章中心对称图形(一)复习与回顾(2)[上学期]
文档属性
| 名称 | 苏科版八上 第三章中心对称图形(一)复习与回顾(2)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 98.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-16 12:27:00 | ||
图片预览




文档简介
课件23张PPT。第三章 中心对称与
中心对称图形复习与回顾(2)矩形的定义 有一个角是直角的平行四边形叫做矩形,通常也叫长方形。 矩形的性质 ①矩形是特殊的平行四边形,它具有平行四边形的一切性质;
②矩形既是轴对称图形也是中心对称图形,对称轴是对边中点连线所在直线,有两条,对称中心是对角线的交点。
③矩形的对角线相等;
④矩形的四个角都是直角。矩形的判定 ①有一个角是直角的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
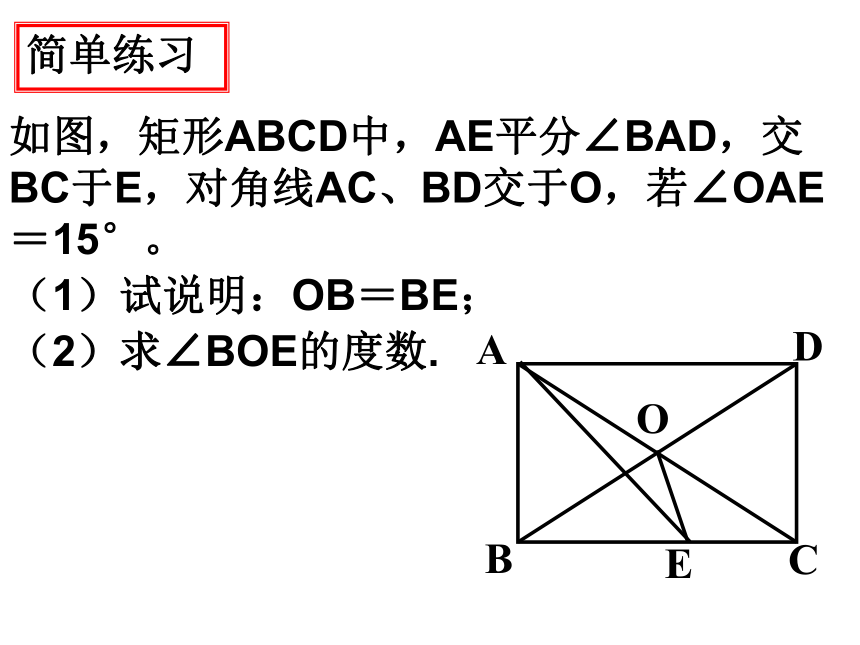
③有3个角是直角的四边形是矩形。简单练习如图,矩形ABCD中,AE平分∠BAD,交BC于E,对角线AC、BD交于O,若∠OAE=15°。
(1)试说明:OB=BE;
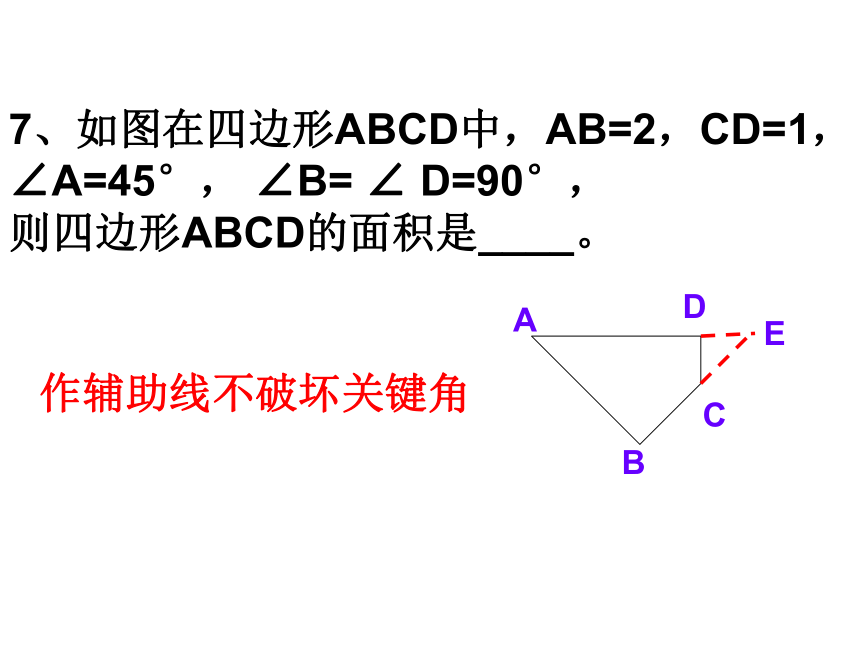
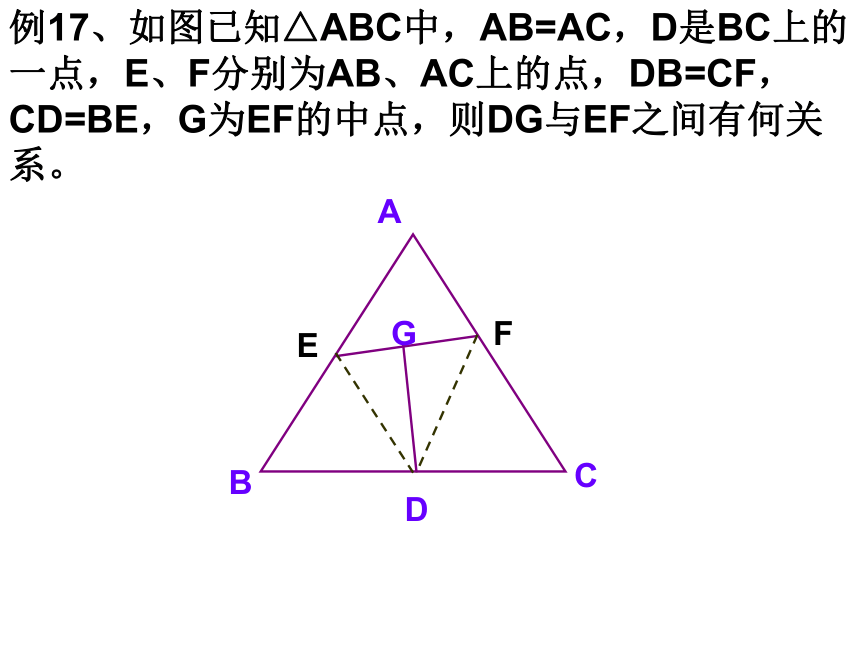
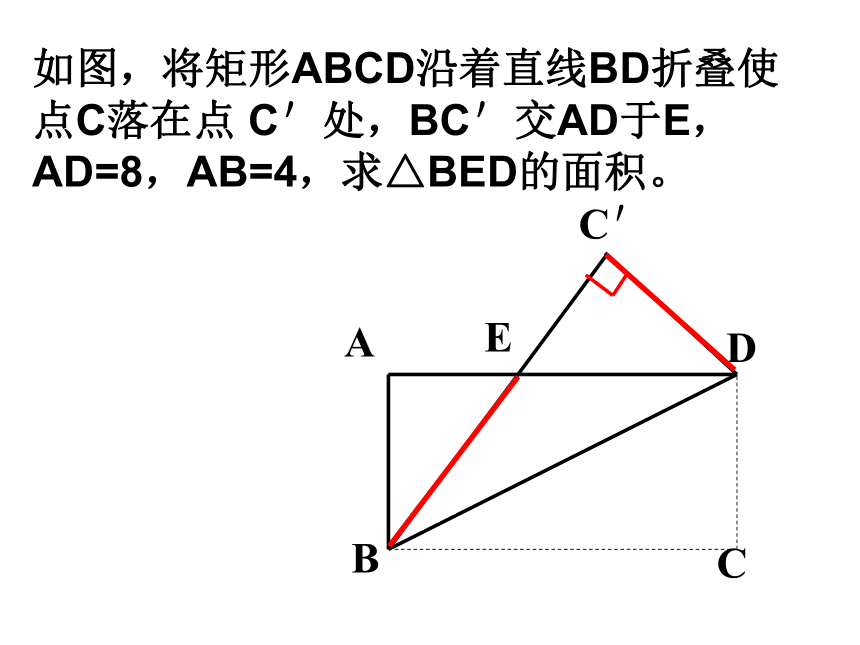
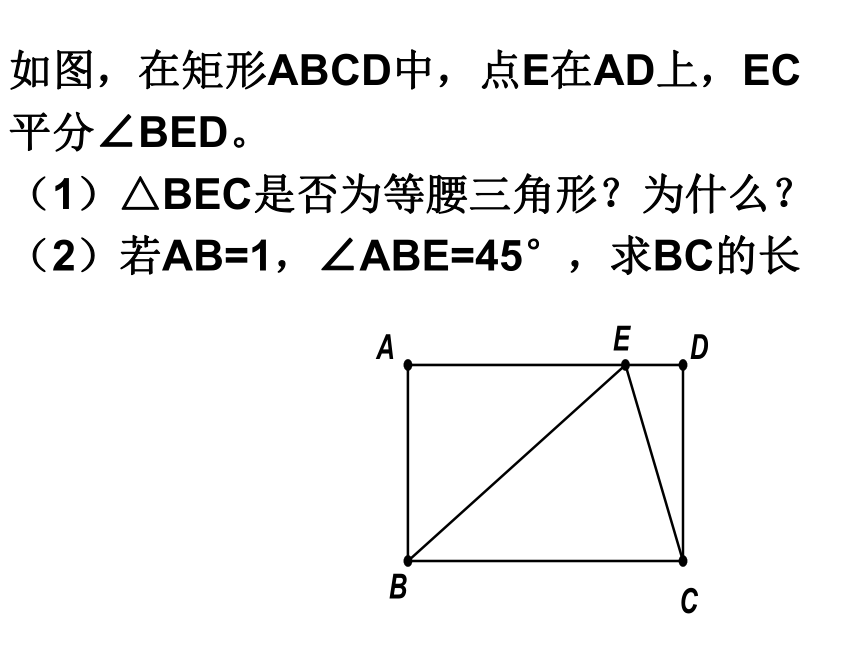
(2)求∠BOE的度数. 7、如图在四边形ABCD中,AB=2,CD=1, ∠A=45°, ∠B= ∠ D=90°, 则四边形ABCD的面积是____。E作辅助线不破坏关键角例17、如图已知△ABC中,AB=AC,D是BC上的一点,E、F分别为AB、AC上的点,DB=CF,CD=BE,G为EF的中点,则DG与EF之间有何关系。GACBDEF如图,将矩形ABCD沿着直线BD折叠使点C落在点 C'处,BC'交AD于E,AD=8,AB=4,求△BED的面积。 如图,在矩形ABCD中,点E在AD上,EC平分∠BED。
(1)△BEC是否为等腰三角形?为什么?
(2)若AB=1,∠ABE=45°,求BC的长菱形的定义 有一组邻边相等的平行四边形叫做菱形。菱形的性质 ①菱形是特殊的平行四边形,它具有平行四边形的一切性质;
②菱形既是轴对称图形也是中心对称图形,对称轴是两条对角线所在直线,对称中心是对角线的交点。
③菱形的四条边相等;
④菱形的对角线互相垂直,并且每一条对角线平分一组对角 菱形的判定 ①有一组邻边相等的平行四边形是菱形;
②四边都相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形 菱形的面积特殊计算公式菱形面积等于对角线积的一半简单应用已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求AC的长及菱形的面积。如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F。四边形AFCE是菱形吗?为什么? 正方形的定义 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形 正方形的性质 ①正方形具有矩形的性质,同时又具有菱形的性质。
②正方形既是轴对称图形也是中心对称图形,对称轴有四条,对称中心是对角线的交点 正方形的判定 ①有一组邻边相等并且有一个角是直角的平行四边形是正方形
②有一组邻边相等矩形形是正方形;
③有一个角是直角的菱形是正方形 平行四边形、矩形、菱形、正方形之间的关系 如图,点E是正方形ABCD的边BC延长线上的一点,且CE=AC,若AE交CD于点F,则∠E= °;∠AFC= _______.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于E,交CD于F, 则∠BEC=____度. 如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由.
1)如图(1)正方形ABCD中,AE⊥BF于点G,试说明AE=BF。 (2)如果把线段BF变动位置如图(2),其余条件不变,(1)中结论还成立吗?(3)如果把AE与BF变动位置如图(3),结论还成立吗?简单应用如图,在⊿ABC中,∠C=90°,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F。问四边形CFDE是正方形吗?请说明理由 G已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角CAM的平分线,CE⊥AN,垂足为E,连接DE
(1)求证:四边形ADCE为矩形
(2)求证:DF∥AB,DF= AB
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?简述你的理由。 已知:如图,△ABC和△ECD都是等腰直角三角形,,D为AB边上一点,
求证:(1)△ACE≌△BCD;
(2)例16、如图,已知过△ABC的顶点C在△ ABC的形外作直线EF,若AE⊥EF,BF⊥EF,D是AB的中点; (1)试说明△ DEF是等腰三角形; (2)如果直线EF经过△ ABC的内部,其余条件不变,则上述结论是否成立?说明理由。EADBFCGE1F1H
中心对称图形复习与回顾(2)矩形的定义 有一个角是直角的平行四边形叫做矩形,通常也叫长方形。 矩形的性质 ①矩形是特殊的平行四边形,它具有平行四边形的一切性质;
②矩形既是轴对称图形也是中心对称图形,对称轴是对边中点连线所在直线,有两条,对称中心是对角线的交点。
③矩形的对角线相等;
④矩形的四个角都是直角。矩形的判定 ①有一个角是直角的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
③有3个角是直角的四边形是矩形。简单练习如图,矩形ABCD中,AE平分∠BAD,交BC于E,对角线AC、BD交于O,若∠OAE=15°。
(1)试说明:OB=BE;
(2)求∠BOE的度数. 7、如图在四边形ABCD中,AB=2,CD=1, ∠A=45°, ∠B= ∠ D=90°, 则四边形ABCD的面积是____。E作辅助线不破坏关键角例17、如图已知△ABC中,AB=AC,D是BC上的一点,E、F分别为AB、AC上的点,DB=CF,CD=BE,G为EF的中点,则DG与EF之间有何关系。GACBDEF如图,将矩形ABCD沿着直线BD折叠使点C落在点 C'处,BC'交AD于E,AD=8,AB=4,求△BED的面积。 如图,在矩形ABCD中,点E在AD上,EC平分∠BED。
(1)△BEC是否为等腰三角形?为什么?
(2)若AB=1,∠ABE=45°,求BC的长菱形的定义 有一组邻边相等的平行四边形叫做菱形。菱形的性质 ①菱形是特殊的平行四边形,它具有平行四边形的一切性质;
②菱形既是轴对称图形也是中心对称图形,对称轴是两条对角线所在直线,对称中心是对角线的交点。
③菱形的四条边相等;
④菱形的对角线互相垂直,并且每一条对角线平分一组对角 菱形的判定 ①有一组邻边相等的平行四边形是菱形;
②四边都相等的四边形是菱形;
③对角线互相垂直的平行四边形是菱形 菱形的面积特殊计算公式菱形面积等于对角线积的一半简单应用已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求AC的长及菱形的面积。如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F。四边形AFCE是菱形吗?为什么? 正方形的定义 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形 正方形的性质 ①正方形具有矩形的性质,同时又具有菱形的性质。
②正方形既是轴对称图形也是中心对称图形,对称轴有四条,对称中心是对角线的交点 正方形的判定 ①有一组邻边相等并且有一个角是直角的平行四边形是正方形
②有一组邻边相等矩形形是正方形;
③有一个角是直角的菱形是正方形 平行四边形、矩形、菱形、正方形之间的关系 如图,点E是正方形ABCD的边BC延长线上的一点,且CE=AC,若AE交CD于点F,则∠E= °;∠AFC= _______.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于E,交CD于F, 则∠BEC=____度. 如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由.
1)如图(1)正方形ABCD中,AE⊥BF于点G,试说明AE=BF。 (2)如果把线段BF变动位置如图(2),其余条件不变,(1)中结论还成立吗?(3)如果把AE与BF变动位置如图(3),结论还成立吗?简单应用如图,在⊿ABC中,∠C=90°,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F。问四边形CFDE是正方形吗?请说明理由 G已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角CAM的平分线,CE⊥AN,垂足为E,连接DE
(1)求证:四边形ADCE为矩形
(2)求证:DF∥AB,DF= AB
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?简述你的理由。 已知:如图,△ABC和△ECD都是等腰直角三角形,,D为AB边上一点,
求证:(1)△ACE≌△BCD;
(2)例16、如图,已知过△ABC的顶点C在△ ABC的形外作直线EF,若AE⊥EF,BF⊥EF,D是AB的中点; (1)试说明△ DEF是等腰三角形; (2)如果直线EF经过△ ABC的内部,其余条件不变,则上述结论是否成立?说明理由。EADBFCGE1F1H
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
