2.2.2化学反应的计算 课件(共41张PPT)高中化学苏教版必修第一册
文档属性
| 名称 | 2.2.2化学反应的计算 课件(共41张PPT)高中化学苏教版必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2023-07-15 21:25:16 | ||
图片预览










文档简介
(共41张PPT)
第二单元 溶液组成的定量研究
第2课时 化学反应的计算
课标定位素养阐释
1.能准确描述物质的量在化学方程式计算中的应用步骤及方法。以定量的视角得出化学反应中相关量的关系。
2.能说出化学计算中的常用方法,建立化学方程式计算模型。
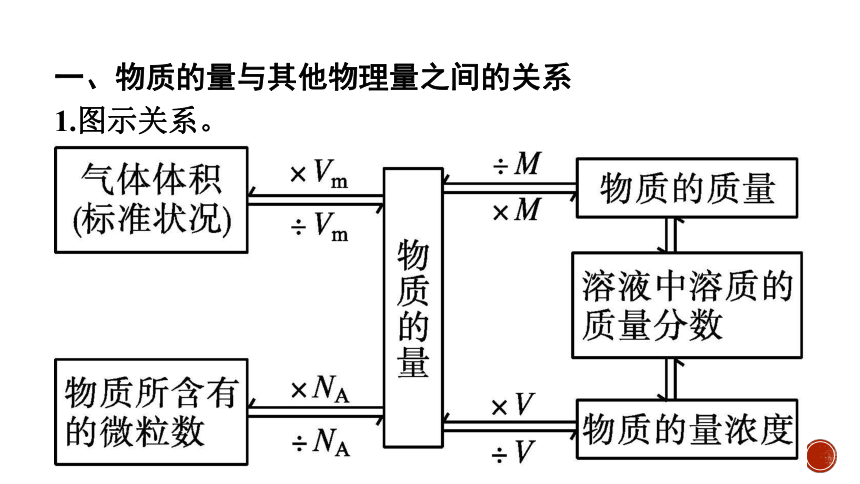
一、物质的量与其他物理量之间的关系
1.图示关系。
2.计算公式。
二、物质的量在化学方程式计算中的应用
1.化学方程式中各物质的化学计量数之比等于各物质的物质的量之比,也等于各物质的微粒数之比,对于有气体参加的反应还等于气体体积之比(相同状况下)。
2.物质的量应用于化学方程式中的计算步骤。
(1)设:设所求物质的物质的量为n(B) 。
(2)写:写出有关的化学方程式。
(3)标:在化学方程式有关物质的化学式下面标出已知和未知的有关物理量的关系,再代入已知量和未知量。
(4)列:列出含有未知量的数学表达式。
(5)算:根据表达式进行计算。
(6)答:简明地写出答案。
【自主思考1】 将6.5 g 锌放入足量的盐酸中充分反应,生成标准状况下氢气的体积是多少
提示:n(Zn)= =0.1 mol。根据化学方程式Zn+2HCl ══ZnCl2+H2↑可知,n(H2)=n(Zn)=0.1 mol,V(H2)=n·Vm=0.1 mol×22.4 L·mol-1=2.24 L。
【自主思考2】 将6.5 g 锌放入含有0.1 mol HCl的盐酸中,充分反应,生成标准状况下氢气的体积是多少
提示:若已知两种或两种以上反应物的量,计算时首先要判断哪种物质过量,以完全反应的物质的有关物理量为标准进行计算。n(Zn)= =0.1 mol,n(HCl)=0.1 mol,根据化学方程式Zn+2HCl══ZnCl2+H2↑可知Zn过量,应根据HCl的物质的量进行计算。n(H2)= n(HCl)=0.05 mol,V(H2)=n·Vm= 0.05 mol×22.4 L·mol-1=1.12 L。
【效果自测】
1.对于反应:2A(g)+2B(g)══3C(g)+D(g),化学计量数之比与下列各项不等的是( )。
A.分子数之比 B.物质的量之比
C.质量之比 D.体积之比(相同状况)
答案:C
2.若56 g铁粉完全氧化成氧化铁,需要消耗氧气的质量为( )。
A.24 g B.32 g C.21 g D.16 g
答案:A
3.标准状况下,3.25 g锌与足量的盐酸反应生成x L氢气,下列比例式正确的是( )。
A.Zn+2HCl══ZnCl2+H2↑
1 mol 1 mol
3.25 g x L
B.Zn+2HCl══ZnCl2+H2↑
65 g 1 L
3.25 g x L
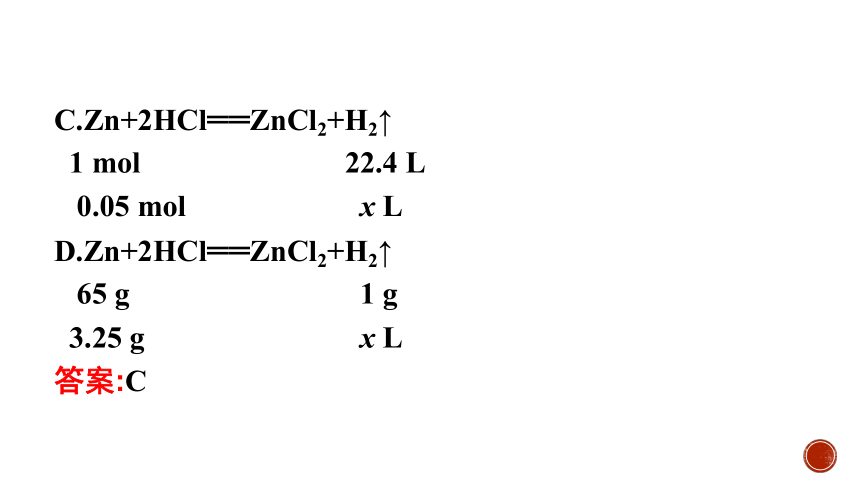
C.Zn+2HCl══ZnCl2+H2↑
1 mol 22.4 L
0.05 mol x L
D.Zn+2HCl══ZnCl2+H2↑
65 g 1 g
3.25 g x L
答案:C
问题引领
化学方程式表示的意义(或提供的信息)
探究任务1 物质的量在化学方程式计算中的应用
1.化学方程式H2+Cl2 2HCl的含义有哪些 (从物质的转化、微观粒子的数目、质量、物质的量4个方面分析)
提示:物质的转化:氢气和氯气在点燃条件下生成氯化氢;
微观粒子的数目:一个氢气分子与一个氯气分子结合生成两个氯化氢分子;
质量:每2 g氢气与71 g氯气反应生成73 g氯化氢;
物质的量:1 mol H2与1 mol Cl2完全反应生成2 mol HCl。
2.化学反应前后质量是守恒的,那么物质的量也守恒吗
提示:化学方程式中各物质的物质的量之比=各物质的化学计量数之比,所以,化学反应后物质的量可能增加,可能减少,也可能不变。
3.根据化学方程式进行计算时,如果遇到已知物理量与未知物理量不一致时,可以直接列式计算吗
提示:由于同一物质的质量与其物质的量成正比关系,相同状况下,气体体积与物质的量成正比关系,因此根据化学方程式计算时,各物质对应的各物理量的单位上、下必须一致,左、右相互对应即可。
归纳提升
1.化学方程式所表示的意义。
化学方程式既表示化学反应前后的物质变化,也表示反应物和生成物之间的分子数关系、质量关系以及物质的量关系,它还表示反应前后固体的质量差或物质的量的差等差量关系。
以H2和O2反应生成H2O为例,它所反映的关系可以表示为:
2H2+O2 2H2O
化学计量数(ν)之比 2 1 2
质量(m)之比 4 32 36
微粒或分子数(N)之比 2 1 2
物质的量(n)之比 2 1 2
结论:化学方程式中各物质的化学计量数之比等于物质的量之比,也等于微粒个数之比。即:
2.物质的量在化学方程式计算中的应用。
学习“物质的量”这一物理量后,可以从一个崭新的视角来认识化学反应。根据化学方程式进行计算时,列比例式不要拘泥于质量之间的正比例关系,只要注意化学计量数,并使上下(同一物质)单位相同,左右(两种物质)单位相对应,都可以列出比例式,直接求解有关量。
例如:对于反应Zn+H2SO4══ZnSO4+H2↑,其意义为:1 mol(65 g) Zn与1 mol H2SO4恰好完全反应生成1 mol(161 g)ZnSO4和1 mol H2,且溶液的质量增加63 g。因此可列出如下比例式:
已知上式中3个量中的任何一个,便可依据比例式求解另外2个量。
典型例题
【例题1】 已知Al与NaOH溶液反应的化学方程式为2Al+2NaOH+2H2O══2NaAlO2+3H2↑。向500 mL NaOH溶液中投入10.8 g Al,两者恰好完全反应,计算:
(1)Al的物质的量。
(2)参加反应的NaOH的物质的量和溶液中NaOH的物质的量浓度。
(3)生成的H2在标准状况下的体积。
答案:解:(1)Al的摩尔质量是27 g·mol-1,
(2)2Al + 2NaOH+2H2O══2NaAlO2+3H2↑
2 2
0.4 mol n(NaOH)
(3)2Al+2NaOH+2H2O══2NaAlO2+3H2↑
2 mol 3×22.4 L
0.4 mol V(H2)
答:(1)Al的物质的量为0.4 mol。
(2)参加反应的NaOH的物质的量为0.4 mol,NaOH的物质的量浓度为0.8 mol·L-1。
(3)生成的H2在标准状况下的体积为13.44 L。
素养提升 1.物质的量是化学计算的工具,解题过程中我们通常会把微粒数、物质的质量、气体物质的体积、溶液的物质的量浓度等转化成物质的量(n= =c·V),再利用相关的关系建立关系式进行解题。
2.物质的量应用于化学反应计算的基本步骤。
【变式训练1】 已知钠与水反应的化学方程式为2Na+2H2O══2NaOH+H2↑。将2.3 g钠投入97.8 g水中,反应完毕后,得到100 mL溶液,求:
(1)产生的氢气在标准状况下的体积。
(2)所得氢氧化钠溶液的溶质质量分数。
(3)所得氢氧化钠溶液的物质的量浓度。
2Na+2H2O══2NaOH+H2↑
2 mol 22.4 L
0.1 mol V(H2)
生成的氢气在标准状况下的体积为V(H2)= =1.12 L。
(2)0.1 mol Na完全反应生成0.1 mol NaOH和0.05 mol H2,氢氧化钠的质量为40 g·mol-1×0.1 mol=4 g,所得溶液质量为2.3 g+97.8 g-2 g·mol-1×0.05 mol=100 g,则所得溶液中氢氧化钠
答:(1)产生的氢气在标准状况下的体积为1.12 L。
(2)所得氢氧化钠溶液的溶质质量分数为4%。
(3)所得氢氧化钠溶液的物质的量浓度为1 mol·L-1。
问题引领
1.将一定量的锌放入盐酸中,完全反应后,溶液质量增加6.3 g,计算参加反应的锌的物质的量。
提示:
Zn+2HCl══ZnCl2+H2↑ Δm
1 mol 63 g
n 6.3 g
n=0.1 mol。
探究任务2 化学计算中常用的三种方法
提示:方法一:根据化学方程式得4FeS2~8SO2~8SO3~8H2SO4,即FeS2~2H2SO4。
方法二:由硫元素守恒得,FeS2~2H2SO4。
归纳提升
1.关系式法。
当已知物和未知物之间是靠多个反应来联系时,可直接确定已知量物质和未知量物质之间的“关系式”。
(1)根据化学方程式确定关系式:写出发生反应的化学方程式,根据量的关系写出关系式。
如:把CO还原Fe2O3生成的CO2通入澄清石灰水中,求生成沉淀的量。
发生反应的化学方程式:
3CO+Fe2O3 2Fe+3CO2,
CO2+Ca(OH)2══CaCO3↓+H2O
则关系式为3CO~3CO2~3CaCO3,即CO~CaCO3。
(2)根据原子守恒确定关系式:上述例子中也可直接根据碳原子守恒得出CO~CaCO3。
2.守恒法。
化学反应的实质是原子的重新组合,依据质量守恒定律,在化学反应中存在一系列守恒关系,如质量守恒、电荷守恒等,利用这些守恒关系解题的方法叫做守恒法。
(1)质量守恒:化学反应前后各物质的质量总和不变。
(2)元素守恒:如工业制硝酸,4NH3+5O2 4NO+6H2O, 2NO+O2══2NO2,3NO2+H2O══2HNO3+NO。经多次氧化和吸收,由氮元素守恒知:NH3~HNO3。
(3)电荷守恒:电荷守恒即对任一电中性的体系,如化合物、混合物、溶液等,正电荷总数和负电荷总数相等。如K2SO4和NaCl的混合溶液中,n(K+)+n(Na+)=2n( )+n(Cl-)。
3.差量法。
根据化学反应前后物质的有关物理量(物质的量或质量或相同状况下气体的体积)发生的变化,找出所谓“理论差量”,该差量的大小与反应物的有关量成正比。差量法就是借助这种比例关系,解决问题的计算方法。解题的一般步骤为:
(1)准确写出有关反应的化学方程式。
(2)找出产生差量的“对象”及“理论差量”。该“理论差量”可以是质量、物质的量、气体体积等,且该差量的大小与参加反应的物质的有关量成正比。
(3)根据化学方程式,从“实际差量”寻找比例关系,列比例式求解。
如Zn+FeSO4══ZnSO4+Fe,反应前后溶液的质量增加(或固体的质量减少),每消耗1 mol Zn,生成1 mol Fe,溶液质量增加(或固体质量减少)65 g-56 g=9 g。
典型例题
【例题2】 把一铁棒插入CuSO4溶液中,过一段时间取出,铁棒质量增加了4 g,求参加反应的Fe的质量。
答案:28 g
解析:
Fe+CuSO4══FeSO4+Cu Δm(质量增加)
56 64 64-56=8
m(Fe) 4 g
m(Fe)=28 g
加热,待其反应后再加入过量盐酸,将生成的气体完全燃烧,共收集得9 g水,则加入的铁粉质量为( )。
A.14 g B.42 g
C.56 g D.28 g
答案:D
解析:设加入的铁粉的质量为x。根据各步反应的定量关系,可列出关系式:
推出:Fe~H2O
56 18
x 9 g
x=28 g,即加入的铁粉为28 g。
第二单元 溶液组成的定量研究
第2课时 化学反应的计算
课标定位素养阐释
1.能准确描述物质的量在化学方程式计算中的应用步骤及方法。以定量的视角得出化学反应中相关量的关系。
2.能说出化学计算中的常用方法,建立化学方程式计算模型。
一、物质的量与其他物理量之间的关系
1.图示关系。
2.计算公式。
二、物质的量在化学方程式计算中的应用
1.化学方程式中各物质的化学计量数之比等于各物质的物质的量之比,也等于各物质的微粒数之比,对于有气体参加的反应还等于气体体积之比(相同状况下)。
2.物质的量应用于化学方程式中的计算步骤。
(1)设:设所求物质的物质的量为n(B) 。
(2)写:写出有关的化学方程式。
(3)标:在化学方程式有关物质的化学式下面标出已知和未知的有关物理量的关系,再代入已知量和未知量。
(4)列:列出含有未知量的数学表达式。
(5)算:根据表达式进行计算。
(6)答:简明地写出答案。
【自主思考1】 将6.5 g 锌放入足量的盐酸中充分反应,生成标准状况下氢气的体积是多少
提示:n(Zn)= =0.1 mol。根据化学方程式Zn+2HCl ══ZnCl2+H2↑可知,n(H2)=n(Zn)=0.1 mol,V(H2)=n·Vm=0.1 mol×22.4 L·mol-1=2.24 L。
【自主思考2】 将6.5 g 锌放入含有0.1 mol HCl的盐酸中,充分反应,生成标准状况下氢气的体积是多少
提示:若已知两种或两种以上反应物的量,计算时首先要判断哪种物质过量,以完全反应的物质的有关物理量为标准进行计算。n(Zn)= =0.1 mol,n(HCl)=0.1 mol,根据化学方程式Zn+2HCl══ZnCl2+H2↑可知Zn过量,应根据HCl的物质的量进行计算。n(H2)= n(HCl)=0.05 mol,V(H2)=n·Vm= 0.05 mol×22.4 L·mol-1=1.12 L。
【效果自测】
1.对于反应:2A(g)+2B(g)══3C(g)+D(g),化学计量数之比与下列各项不等的是( )。
A.分子数之比 B.物质的量之比
C.质量之比 D.体积之比(相同状况)
答案:C
2.若56 g铁粉完全氧化成氧化铁,需要消耗氧气的质量为( )。
A.24 g B.32 g C.21 g D.16 g
答案:A
3.标准状况下,3.25 g锌与足量的盐酸反应生成x L氢气,下列比例式正确的是( )。
A.Zn+2HCl══ZnCl2+H2↑
1 mol 1 mol
3.25 g x L
B.Zn+2HCl══ZnCl2+H2↑
65 g 1 L
3.25 g x L
C.Zn+2HCl══ZnCl2+H2↑
1 mol 22.4 L
0.05 mol x L
D.Zn+2HCl══ZnCl2+H2↑
65 g 1 g
3.25 g x L
答案:C
问题引领
化学方程式表示的意义(或提供的信息)
探究任务1 物质的量在化学方程式计算中的应用
1.化学方程式H2+Cl2 2HCl的含义有哪些 (从物质的转化、微观粒子的数目、质量、物质的量4个方面分析)
提示:物质的转化:氢气和氯气在点燃条件下生成氯化氢;
微观粒子的数目:一个氢气分子与一个氯气分子结合生成两个氯化氢分子;
质量:每2 g氢气与71 g氯气反应生成73 g氯化氢;
物质的量:1 mol H2与1 mol Cl2完全反应生成2 mol HCl。
2.化学反应前后质量是守恒的,那么物质的量也守恒吗
提示:化学方程式中各物质的物质的量之比=各物质的化学计量数之比,所以,化学反应后物质的量可能增加,可能减少,也可能不变。
3.根据化学方程式进行计算时,如果遇到已知物理量与未知物理量不一致时,可以直接列式计算吗
提示:由于同一物质的质量与其物质的量成正比关系,相同状况下,气体体积与物质的量成正比关系,因此根据化学方程式计算时,各物质对应的各物理量的单位上、下必须一致,左、右相互对应即可。
归纳提升
1.化学方程式所表示的意义。
化学方程式既表示化学反应前后的物质变化,也表示反应物和生成物之间的分子数关系、质量关系以及物质的量关系,它还表示反应前后固体的质量差或物质的量的差等差量关系。
以H2和O2反应生成H2O为例,它所反映的关系可以表示为:
2H2+O2 2H2O
化学计量数(ν)之比 2 1 2
质量(m)之比 4 32 36
微粒或分子数(N)之比 2 1 2
物质的量(n)之比 2 1 2
结论:化学方程式中各物质的化学计量数之比等于物质的量之比,也等于微粒个数之比。即:
2.物质的量在化学方程式计算中的应用。
学习“物质的量”这一物理量后,可以从一个崭新的视角来认识化学反应。根据化学方程式进行计算时,列比例式不要拘泥于质量之间的正比例关系,只要注意化学计量数,并使上下(同一物质)单位相同,左右(两种物质)单位相对应,都可以列出比例式,直接求解有关量。
例如:对于反应Zn+H2SO4══ZnSO4+H2↑,其意义为:1 mol(65 g) Zn与1 mol H2SO4恰好完全反应生成1 mol(161 g)ZnSO4和1 mol H2,且溶液的质量增加63 g。因此可列出如下比例式:
已知上式中3个量中的任何一个,便可依据比例式求解另外2个量。
典型例题
【例题1】 已知Al与NaOH溶液反应的化学方程式为2Al+2NaOH+2H2O══2NaAlO2+3H2↑。向500 mL NaOH溶液中投入10.8 g Al,两者恰好完全反应,计算:
(1)Al的物质的量。
(2)参加反应的NaOH的物质的量和溶液中NaOH的物质的量浓度。
(3)生成的H2在标准状况下的体积。
答案:解:(1)Al的摩尔质量是27 g·mol-1,
(2)2Al + 2NaOH+2H2O══2NaAlO2+3H2↑
2 2
0.4 mol n(NaOH)
(3)2Al+2NaOH+2H2O══2NaAlO2+3H2↑
2 mol 3×22.4 L
0.4 mol V(H2)
答:(1)Al的物质的量为0.4 mol。
(2)参加反应的NaOH的物质的量为0.4 mol,NaOH的物质的量浓度为0.8 mol·L-1。
(3)生成的H2在标准状况下的体积为13.44 L。
素养提升 1.物质的量是化学计算的工具,解题过程中我们通常会把微粒数、物质的质量、气体物质的体积、溶液的物质的量浓度等转化成物质的量(n= =c·V),再利用相关的关系建立关系式进行解题。
2.物质的量应用于化学反应计算的基本步骤。
【变式训练1】 已知钠与水反应的化学方程式为2Na+2H2O══2NaOH+H2↑。将2.3 g钠投入97.8 g水中,反应完毕后,得到100 mL溶液,求:
(1)产生的氢气在标准状况下的体积。
(2)所得氢氧化钠溶液的溶质质量分数。
(3)所得氢氧化钠溶液的物质的量浓度。
2Na+2H2O══2NaOH+H2↑
2 mol 22.4 L
0.1 mol V(H2)
生成的氢气在标准状况下的体积为V(H2)= =1.12 L。
(2)0.1 mol Na完全反应生成0.1 mol NaOH和0.05 mol H2,氢氧化钠的质量为40 g·mol-1×0.1 mol=4 g,所得溶液质量为2.3 g+97.8 g-2 g·mol-1×0.05 mol=100 g,则所得溶液中氢氧化钠
答:(1)产生的氢气在标准状况下的体积为1.12 L。
(2)所得氢氧化钠溶液的溶质质量分数为4%。
(3)所得氢氧化钠溶液的物质的量浓度为1 mol·L-1。
问题引领
1.将一定量的锌放入盐酸中,完全反应后,溶液质量增加6.3 g,计算参加反应的锌的物质的量。
提示:
Zn+2HCl══ZnCl2+H2↑ Δm
1 mol 63 g
n 6.3 g
n=0.1 mol。
探究任务2 化学计算中常用的三种方法
提示:方法一:根据化学方程式得4FeS2~8SO2~8SO3~8H2SO4,即FeS2~2H2SO4。
方法二:由硫元素守恒得,FeS2~2H2SO4。
归纳提升
1.关系式法。
当已知物和未知物之间是靠多个反应来联系时,可直接确定已知量物质和未知量物质之间的“关系式”。
(1)根据化学方程式确定关系式:写出发生反应的化学方程式,根据量的关系写出关系式。
如:把CO还原Fe2O3生成的CO2通入澄清石灰水中,求生成沉淀的量。
发生反应的化学方程式:
3CO+Fe2O3 2Fe+3CO2,
CO2+Ca(OH)2══CaCO3↓+H2O
则关系式为3CO~3CO2~3CaCO3,即CO~CaCO3。
(2)根据原子守恒确定关系式:上述例子中也可直接根据碳原子守恒得出CO~CaCO3。
2.守恒法。
化学反应的实质是原子的重新组合,依据质量守恒定律,在化学反应中存在一系列守恒关系,如质量守恒、电荷守恒等,利用这些守恒关系解题的方法叫做守恒法。
(1)质量守恒:化学反应前后各物质的质量总和不变。
(2)元素守恒:如工业制硝酸,4NH3+5O2 4NO+6H2O, 2NO+O2══2NO2,3NO2+H2O══2HNO3+NO。经多次氧化和吸收,由氮元素守恒知:NH3~HNO3。
(3)电荷守恒:电荷守恒即对任一电中性的体系,如化合物、混合物、溶液等,正电荷总数和负电荷总数相等。如K2SO4和NaCl的混合溶液中,n(K+)+n(Na+)=2n( )+n(Cl-)。
3.差量法。
根据化学反应前后物质的有关物理量(物质的量或质量或相同状况下气体的体积)发生的变化,找出所谓“理论差量”,该差量的大小与反应物的有关量成正比。差量法就是借助这种比例关系,解决问题的计算方法。解题的一般步骤为:
(1)准确写出有关反应的化学方程式。
(2)找出产生差量的“对象”及“理论差量”。该“理论差量”可以是质量、物质的量、气体体积等,且该差量的大小与参加反应的物质的有关量成正比。
(3)根据化学方程式,从“实际差量”寻找比例关系,列比例式求解。
如Zn+FeSO4══ZnSO4+Fe,反应前后溶液的质量增加(或固体的质量减少),每消耗1 mol Zn,生成1 mol Fe,溶液质量增加(或固体质量减少)65 g-56 g=9 g。
典型例题
【例题2】 把一铁棒插入CuSO4溶液中,过一段时间取出,铁棒质量增加了4 g,求参加反应的Fe的质量。
答案:28 g
解析:
Fe+CuSO4══FeSO4+Cu Δm(质量增加)
56 64 64-56=8
m(Fe) 4 g
m(Fe)=28 g
加热,待其反应后再加入过量盐酸,将生成的气体完全燃烧,共收集得9 g水,则加入的铁粉质量为( )。
A.14 g B.42 g
C.56 g D.28 g
答案:D
解析:设加入的铁粉的质量为x。根据各步反应的定量关系,可列出关系式:
推出:Fe~H2O
56 18
x 9 g
x=28 g,即加入的铁粉为28 g。
