27.2.1相似三角形的判定(第1课时)[下学期]
文档属性
| 名称 | 27.2.1相似三角形的判定(第1课时)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 101.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-17 08:07:00 | ||
图片预览


文档简介
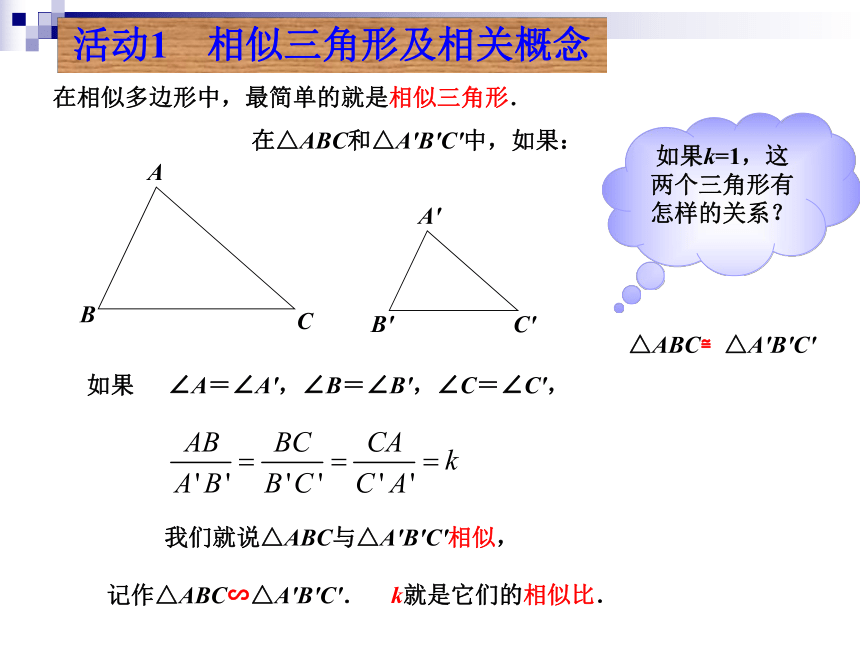
课件9张PPT。27.2 相似三角形27.2.1 相似三角形的判定(第1课时)义务教育课程标准实验教科书九年级 上册人民教育出版社在相似多边形中,最简单的就是相似三角形.
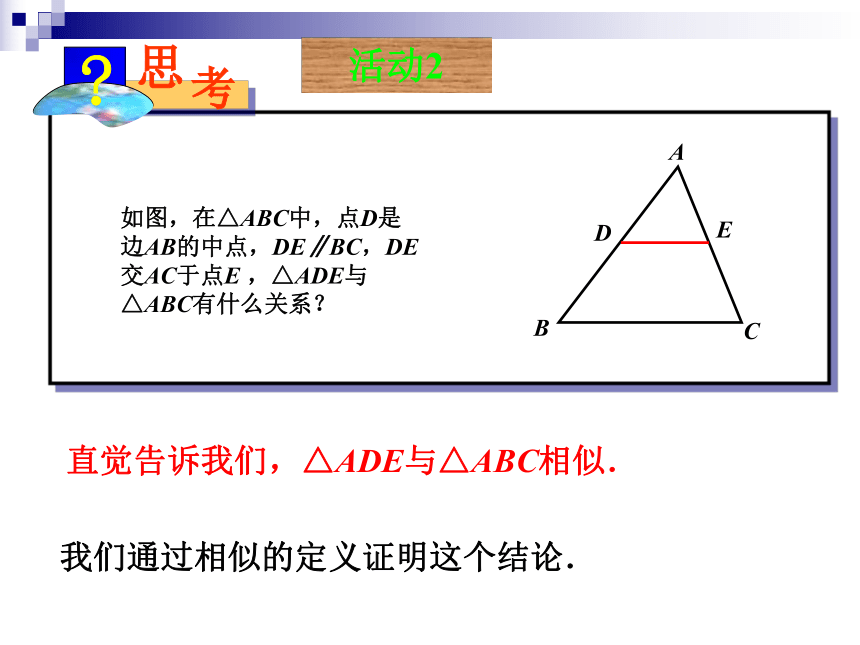
在△ABC和△A'B'C'中,如果:如果 ∠A=∠A',∠B=∠B',∠C=∠C',我们就说△ABC与△A'B'C'相似,如果k=1,这两个三角形有怎样的关系?活动1 相似三角形及相关概念△ABC≌△A'B'C'记作△ABC∽△A'B'C'.k就是它们的相似比.如图,在△ABC中,点D是边AB的中点,DE∥BC,DE交AC于点E ,△ADE与△ABC有什么关系?ABCDE我们通过相似的定义证明这个结论.活动2直觉告诉我们,△ADE与△ABC相似.这样,我们证明了△ADE和△ABC的对应角相等,对应边的比相等,所以它们相似,相似比为先证明两个三角形的对应角相等.在△ADE与△ABC中,∠A=∠A∵DE∥BC∴∠ADE=∠B,∠AED=∠C再证明两个三角形的对应边的比相等.过点E作EF∥AB,EF交BC于点F.在 BFED中,DE=BF,DB=EF∵AD=BD= AB∴AD=EF又∠A=∠1,∠2=∠C∴△ADE≌△EFC∴AE=EC= ACDE=FC=BF= BCABCDEF12ABCDE改变点D在AB上的位置,继续观察图形,进一步想 △ADE与△ABC是否存在着相似关系. 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.证明:过点E作EF//AB,交BC于点F∵DE//BC,DF//AB(平行于三角形一边的直线截其它两边所得的对应线段成比例)∵四边形DEFB是平行四边形,F学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?活动3在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与邻座交流一下,看看是否有同样的结论.如图在△ABC和△A'B'C'中,
求证: △ABC∽△A'B'C'这两个三角形是相似的.证明:在线段A'B'(或它的延长线)上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,根据前面的结论可得△A'DE∽△A'B'C'同理 DE=BC∴△A'DE≌△ABC∴△ABC∽△A'B'C'A'B'C'DE由此我们得到利用三边判定三角形相似的方法:如果两个三角形的三组对应边的比
相等,那么这两个三角形相似.△ABC ∽ △A'B'C'
在△ABC和△A'B'C'中,如果:如果 ∠A=∠A',∠B=∠B',∠C=∠C',我们就说△ABC与△A'B'C'相似,如果k=1,这两个三角形有怎样的关系?活动1 相似三角形及相关概念△ABC≌△A'B'C'记作△ABC∽△A'B'C'.k就是它们的相似比.如图,在△ABC中,点D是边AB的中点,DE∥BC,DE交AC于点E ,△ADE与△ABC有什么关系?ABCDE我们通过相似的定义证明这个结论.活动2直觉告诉我们,△ADE与△ABC相似.这样,我们证明了△ADE和△ABC的对应角相等,对应边的比相等,所以它们相似,相似比为先证明两个三角形的对应角相等.在△ADE与△ABC中,∠A=∠A∵DE∥BC∴∠ADE=∠B,∠AED=∠C再证明两个三角形的对应边的比相等.过点E作EF∥AB,EF交BC于点F.在 BFED中,DE=BF,DB=EF∵AD=BD= AB∴AD=EF又∠A=∠1,∠2=∠C∴△ADE≌△EFC∴AE=EC= ACDE=FC=BF= BCABCDEF12ABCDE改变点D在AB上的位置,继续观察图形,进一步想 △ADE与△ABC是否存在着相似关系. 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.证明:过点E作EF//AB,交BC于点F∵DE//BC,DF//AB(平行于三角形一边的直线截其它两边所得的对应线段成比例)∵四边形DEFB是平行四边形,F学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?活动3在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与邻座交流一下,看看是否有同样的结论.如图在△ABC和△A'B'C'中,
求证: △ABC∽△A'B'C'这两个三角形是相似的.证明:在线段A'B'(或它的延长线)上截取A'D=AB,过点D作DE∥B'C',交A'C'于点E,根据前面的结论可得△A'DE∽△A'B'C'同理 DE=BC∴△A'DE≌△ABC∴△ABC∽△A'B'C'A'B'C'DE由此我们得到利用三边判定三角形相似的方法:如果两个三角形的三组对应边的比
相等,那么这两个三角形相似.△ABC ∽ △A'B'C'
