人教版六年级上册第五单元圆综合质量检测卷三(含答案)
文档属性
| 名称 | 人教版六年级上册第五单元圆综合质量检测卷三(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 375.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-14 00:00:00 | ||
图片预览




文档简介
人教版六年级上册第五单元圆综合质量检测卷三
一、选择题(满分16分)
1.大圆与小圆的半径的比是3∶2,下面选项中错误的是( )。
A.它们的直径的比是3∶2 B.它们的周长的比是3∶2
C.它们的面积的比是3∶2 D.它们的面积的比是9∶4
2.圆的半径扩大到原来的5倍,圆的面积扩大到原来的( )。
A.5倍 B.10倍 C.25倍 D.无法确定
3.画圆时,圆的周长为31.4cm,那么圆规两脚尖的距离为( )。
A.1cm B.2.5cm C.5cm D.10cm
4.一个圆形蓄水池的周长是25.12m。它的占地面积是( )m2。
A.200.96 B.50.24 C.25.12
5.如下图所示,大半圆面积与小半圆面积的最简整数比是( )。
A.1∶1 B.2∶1 C.4∶1 D.1∶4
6.左图中长方形的面积是6cm2,那么半圆的面积是( )。
A.4.71 B.9.42 C.5
7.如下图,大圆直径2cm,小圆贴着大圆的内侧从P点开始按箭头所指方向滚动,小圆至少需要滚动( )周才能回到P点。
A.2 B.3 C.4
8.圆规两脚之间的距离如图床示,用此时的圆规所画出的圆的周长是( )cm。
A.3π B.4π C.6π
二、填空题(满分16分)
9.下图中长方形和圆的面积相等,长方形的长是6.28cm,则阴影部分的面积是( )cm2。
10.在一张长10cm,宽6cm的长方形纸片上画一个最大的半圆,这个半圆的周长是( )cm。
11.用一根31.4米的铁丝弯成一个圆形铁圈,铁圈的直径是( ),面积是( )。
12.一个圆的周长是31.4分米,它的面积是( )平方分米。
13.把一个圆平均分成若干(偶数)等份,然后剪开,拼成一个近似的长方形,这个长方形的长近似于( ),宽近似于( )。
14.如果把一个圆缩小,其周长由原来的31.4厘米变成15.7厘米,那么它的面积就变成原来的( )。
15.花园小区修建一个半径是4米的圆形花坛,在花坛周围又修建了一条1米宽的小路,这条小路的面积是( )平方米。
16.如图中圆的面积是,平行四边形的面积是________,三角形的面积是________。
三、判断题(满分8分)
17.甲乙两个圆的半径比是2∶9,它们的周长比也是2∶9。( )
18.半圆、正方形、长方形与平行四边形都是轴对称图形。( )
19.周长相等的两个圆,面积一定相等。( )
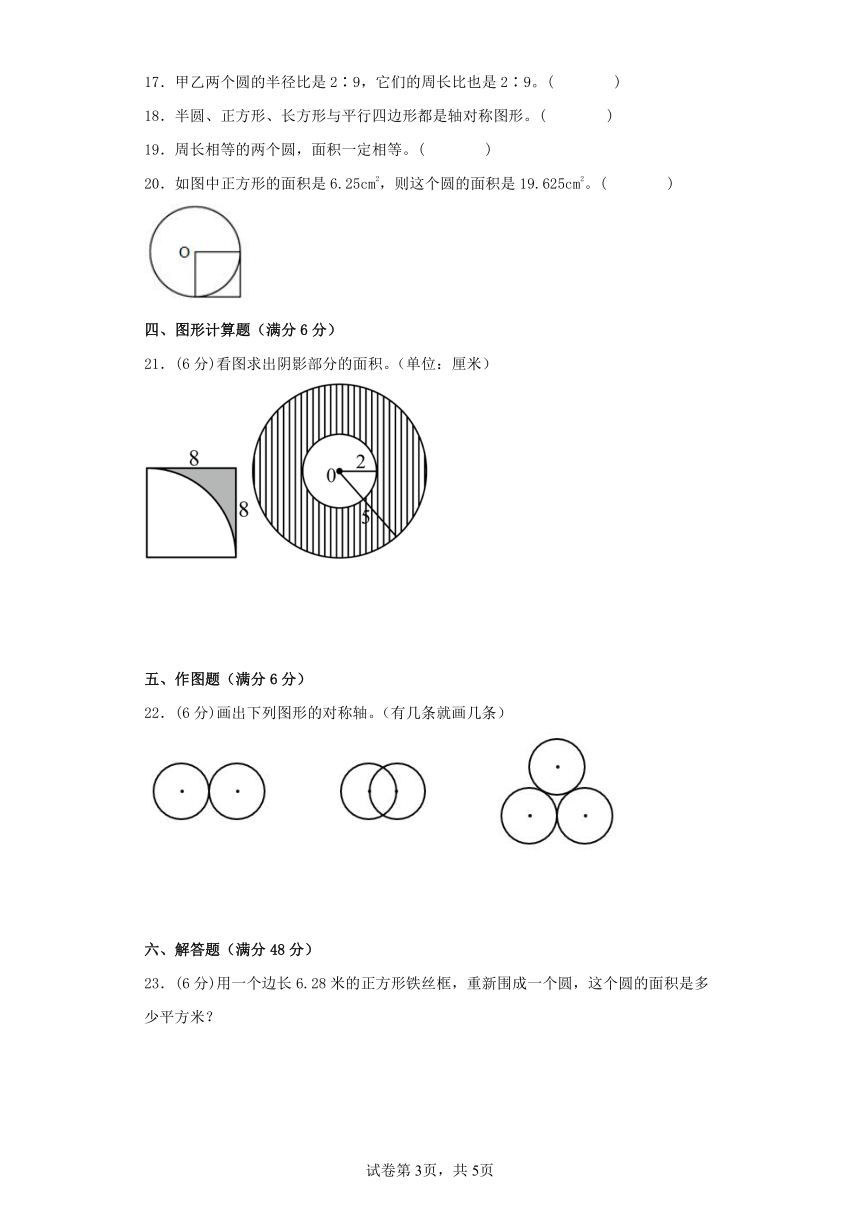
20.如图中正方形的面积是6.25cm2,则这个圆的面积是19.625cm2。( )
四、图形计算题(满分6分)
21.(6分)看图求出阴影部分的面积。(单位:厘米)
五、作图题(满分6分)
22.(6分)画出下列图形的对称轴。(有几条就画几条)
六、解答题(满分48分)
23.(6分)用一个边长6.28米的正方形铁丝框,重新围成一个圆,这个圆的面积是多少平方米?
24.(6分)一辆自行车车轮的外直径为72cm,王帆骑这辆自行车通过一座长2260.8m的大桥,如果期间车轮平均每分钟转100圈,那么他通过这座大桥需要几分钟?
25.(6分)餐厅有两种圆桌。小圆桌桌面直径是1.6米,是大圆桌的。大圆桌面积比小圆桌大约大多少平方米?(得数保留两位小数)
26.(6分)一个鸡舍依墙而建,呈半圆形,半径是10米。
(1)修这个鸡舍需要多长的栅栏?
(2)如果要扩建这个鸡舍,把它的直径增加2米。鸡舍的面积增加了多少?
27.(6分)学校要修建一个直径是6米的圆形花园,花园外留出1米宽的小路。这块场地占地面积是多少?
28.(6分)一个圆形花坛的半径是5米,现在要扩建花坛,将半径增加了3米,这时花坛的占地面积比原来多了多少平方米?
29.(6分)坐落于贵州的“天厦”射电望远惶外侧,直径600米的圆周上建造均匀布置的6座不同高度的馈源支撑塔,以及相关的塔基础、附属设施、防雷接地等。你能算出每两座馈源支撑塔之间的距离是多少吗?
30.(6分)猫和老鼠在一个直径是50米的圆周上的同一地点向相反方向运动,猫每分钟走21.98米,老鼠每分钟走9.42米。当猫和老鼠第一次相遇时,猫比老鼠多走了多少米?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【分析】根据圆的半径比与直径比、周长比相等,面积比等于半径的平方比;据此判断即可。
【详解】大圆与小圆的半径的比是3∶2,所以它们的直径的比是3∶2,它们的周长的比是3∶2,它们的面积比是9∶4。
故答案为:C
【点睛】本题主要考查了圆的半径比、直径比、周长比与面积比的关系及应用。
2.C
【分析】假设出原来圆的半径,利用“”分别求出原来圆的面积和现在圆的面积,最后求出圆的面积扩大的倍数,据此解答。
【详解】假设原来圆的半径为2。
原来圆的面积:
现在圆的面积:
=
=
÷=25
所以,圆的面积扩大到原来的25倍。
故答案为:C
【点睛】掌握圆的面积计算公式是解答题目的关键。
3.C
【分析】画圆时,圆规两脚尖的距离是半径,根据圆的半径=周长÷π÷2,列式计算即可。
【详解】31.4÷3.14÷2=5(cm)
圆规两脚尖的距离为5cm。
故答案为:C
【点睛】关键是熟悉画圆的方法,掌握并灵活运用圆的周长公式。
4.B
【分析】根据圆的周长公式:C=2πr,据此求出圆的半径,再根据圆的面积公式:S=πr2,据此计算即可。
【详解】25.12÷3.14÷2
=8÷2
=4(m)
3.14×42=50.24(m2)
则它的占地面积是50.24m2。
故答案为:B
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
5.C
【分析】根据圆的面积公式S=πr2,代入数据,分别求出大半圆和小半圆的面积,再写出对应的比,化简即可。
【详解】大半圆的面积:3.14×22÷2
=3.14×4÷2
=12.56÷2
=6.28
小半圆的面积:3.14×(2÷2)2÷2
=3.14×1÷2
=3.14÷2
=1.57
6.28∶1.57
=(6.28×100÷157)∶(1.57×100÷157)
=(628÷157)∶(157÷157)
=4∶1
故答案为:C
【点睛】此题主要考查了圆的面积公式的应用,注意因为此题是求两个数的比,不是求具体的数,所以在利用公式时带着π也可以。
6.A
【分析】长方形的长等于圆的直径,宽等于圆的半径,假设圆的半径为r,直径为2r,利用长方形的面积公式,代入求出r2,根据圆的面积公式:S=,代入r2的值,再除以2,即可求出半圆的面积。
【详解】假设圆的半径为r,则直径为2r,
r×2r=6
解:2r2=6
r2=6÷2
r2=3
半圆的面积:
=
=4.71(cm2)
故答案为:A
【点睛】此题的解题关键是利用长方形和圆之间的关系,灵活运用长方形和圆的面积公式,解决实际的问题。
7.A
【分析】根据圆的周长公式C=πd,小圆的直径等于大圆的半径,也就是大圆直径是小圆直径的2倍,因为圆周率是一定的,所以大小圆周长的比等于大小圆直径的比,小圆滚动的周数等于大圆周长是小圆周长的倍数,据此解答即可。
【详解】因为大圆直径是小圆直径的2倍,所以大圆周长是小圆周长的2倍;
故答案为:A
【点睛】此题主要考查圆的周长公式的灵活运用,关键是明确:大小圆周长的比等于大小圆直径的比。
8.B
【分析】圆规的两脚之间的距离就是所画圆的半径,根据直尺上的刻度求出圆的半径,再利用圆的周长公式:C=,代入即可求出所画出的圆的周长。
【详解】3-1=2(cm)
2×π×2=4π(cm)
故答案为:B
【点睛】此题考查了圆的周长的计算应用,关键是明白:圆规的两脚之间的距离就是所画圆的半径。
9.9.42
【分析】长方形的长已知,长方形的宽与圆的半径相等,可以用r来表示,长方形面积=长×宽,圆的面积S=πr2,因为长方形和圆的面积相等,所以6.28×r=πr2,由此可求出圆的半径,阴影部分面积=长方形面积-圆的面积。
【详解】假设圆的半径为r,由分析可知:长方形和圆的面积相等,即6.28×r=πr2。
那么圆的半径为:
6.28÷3.14=2(cm)
阴影部分面积:
6.28×2-×3.14×2×2
=12.56-3.14
=9.42(cm2)
【点睛】本题主要考查圆的面积公式,求得圆的半径是解题的关键。
10.25.7
【分析】在一张长10cm,宽6cm的长方形纸片上画一个最大的半圆,这个半圆的直径最大是10cm,直径÷2=半径,根据半圆的周长=πr+d,列式解答即可。
【详解】10÷2=5(cm)
3.14×5+10
=15.7+10
=25.7(cm)
这个半圆的周长是25.7cm。
【点睛】关键是熟悉半圆的特征,掌握并灵活运用半圆周长公式。
11. 10米 78.5平方米
【分析】圆的周长公式为C=πd,则d=C÷π把圆的周长代入可以求出圆的直径,在通过圆的直径是半径的2倍,求出半径,再利用S=πr2求出这个圆的面积。
【详解】直径:31.4÷3.14=10(米)
半径:10÷2=5(米)
面积:3.14×52=78.5(平方米)
【点睛】熟记并灵活运用圆的周长和面积计算公式是解答题目的关键。
12.78.5
【分析】根据圆的周长公式:C=2πr,据此求出圆的半径;再根据圆的面积公式:S=πr2,据此代入数值进行计算即可求出它的面积。
【详解】31.4÷3.14÷2
=10÷2
=5(分米)
3.14×52=78.5(平方分米)
则它的面积是78.5平方分米。
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
13. 圆周长的一半 圆的半径
【分析】根据圆面积公式推导的过程:把一个圆分成若干等份,拼成的图形近似于长方形,这个长方形的长相当于圆周长的一半,长方形的宽就是圆的半径,据此即可解答。
【详解】由分析可知:
把一个圆平均分成若干(偶数)等份,然后剪开,拼成一个近似的长方形,这个长方形的长近似于圆周长的一半,宽近似于圆的半径。
【点睛】此题考查的目的是理解掌握圆面积公式的推导过程。
14.
【分析】先根据“”求出圆的半径,再利用“”求出原来和现在圆的面积,最后用除法求出现在圆的面积占原来圆面积的分率,据此解答。
【详解】原来的半径:31.4÷3.14÷2
=10÷2
=5(厘米)
原来的面积:3.14×52=78.5(平方厘米)
现在的半径:15.7÷3.14÷2
=5÷2
=2.5(厘米)
现在的面积:3.14×2.52=19.625(平方厘米)
19.625÷78.5=
所以,它的面积就变成原来的。
【点睛】掌握圆的周长和面积的计算公式是解答题目的关键。
15.28.26
【分析】由题意可知,大圆的半径为(4+1)米,小圆的半径为4米,利用“”求出小路的面积,据此解答。
【详解】3.14×[(4+1)2-42]
=3.14×[52-42]
=3.14×[25-16]
=3.14×9
=28.26(平方米)
所以,这条小路的面积是28.26平方米。
【点睛】掌握环形的面积计算公式是解答题目的关键。
16. 24 21
【分析】观察图形可知,三角形和平行四边形的高相当于圆的直径,根据圆的面积公式:S=πr2,据此求出圆的半径,进而求出圆的直径,也就是三角形和平行四边形的高,再根据三角形的面积公式:S=ah÷2,平行四边形的面积公式:S=ah,代入数据计算即可求解。
【详解】28.26÷3.14=9(cm2)
因为3×3=9(cm2),所以圆的半径是3cm。
直径是3×2=6(cm)
7×6÷2
=42÷2
=21(cm2)
4×6=24(cm2)
则平行四边形的面积是24,三角形的面积是21。
【点睛】本题考查三角形、平行四边形和圆的面积,求出圆的半径是解题的关键。
17.√
【分析】根据甲乙两个圆的半径比是2∶9,设甲圆的半径为2r,则乙圆的半径为9r,代入圆的周长公式,表示出各自的周长,再利用比的意义即可求解。
【详解】解:设甲圆的半径为2r,则乙圆的半径为9r,
甲圆的周长=2×π×2r=4πr
乙圆的周长=2×π×9r=18πr
4πr∶18πr
=4∶18
=2∶9
即它们的周长比也是2∶9。
故答案为:√
【点睛】此题主要考查圆的周长的计算方法的灵活应用。
18.×
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】
如上图,半圆、正方形、长方形都是轴对称成图形,有对称轴,平行四边形不是轴对称图形。所以原说法错误。
故答案为:×
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
19.√
【分析】因为半径决定圆的大小,如果两个圆的周长相等,也就是两个圆的半径相等,那么两个圆的面积一定相等。据此判断。
【详解】周长相等的两个圆,面积一定相等。这种说法是正确的。
故答案为:√
【点睛】此题考查的目的是理解掌握圆的周长、面积的意义及应用。关键是明确:半径决定圆的大小。
20.√
【分析】根据题意知:圆的半径等于则正方形的边长,正方形的面积等于圆的半径平方,再根据圆的面积公式S=πr2即可求出圆的面积,由此进行判断。
【详解】3.14×6.25=19.625(cm2)
故答案为:√
【点睛】理解正方形的面积等于圆的半径平方,再代入圆的面积公式是解答本题的关键。
21.13.76平方厘米;65.94平方厘米
【分析】(1)空白部分的面积占整个圆面积的,阴影部分的面积=正方形的面积-圆的面积;
(2)阴影部分是一个圆环,圆环的面积计算公式为“”,把图中数据代入公式计算,据此解答。
【详解】(1)8×8-×82×3.14
=64-16×3.14
=64-50.24
=13.76(平方厘米)
所以,阴影部分的面积是13.76平方厘米。
(2)3.14×(52-22)
=3.14×21
=65.94(平方厘米)
所以,阴影部分的面积是65.94平方厘米。
22.见详解
【分析】如果将一个图形沿着一条直线对折,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。画对称轴时要用虚线。
第一个图形是由左、右2个大小相同的圆相切组成的,可以横着画1条对称轴,也可以竖着画一条对称轴,因此它有2条对称轴。
第二个图形是由左、右2个大小相同的圆相交组成的,可以横着画1条对称轴,也可以竖着画一条对称轴,因此它有2条对称轴。
第三个图形是由3个大小相同的圆组成的,把其中任意1个圆的圆心和另外2个圆的相交处相连并延长,都可以画出对称轴,因此它有3条对称轴。
【详解】如图。
【点睛】找组合图形的对称轴时,要把这些图形看作一个整体,仔细观察,发现对称轴的位置。
23.50.24平方米
【分析】先根据“正方形的周长=边长×4”求出铁丝的总长度,圆的周长等于铁丝的总长度,根据“”求出圆的半径,最后利用“”求出这个圆的面积,据此解答。
【详解】半径:6.28×4÷3.14÷2
=(6.28÷3.14)×(4÷2)
=2×2
=4(米)
面积:3.14×42=50.24(平方米)
答:这个圆的面积是50.24平方米。
【点睛】掌握圆的周长和面积计算公式是解答题目的关键。
24.10分钟
【分析】根据圆的周长=πd,求出车轮转一圈行进的距离,车轮周长×每分钟转动圈数=每分钟行驶距离,统一单位,根据时间=路程÷速度,列式解答即可。
【详解】3.14×72×100=22608(厘米)=226.08(米)
2260.8÷226.08=10(分钟)
答:他通过这座大桥需要10分钟。
【点睛】关键是掌握圆的周长公式,理解速度、时间、路程之间的关系。
25.1.13平方米
【分析】根据题意,小圆桌桌面直径是大圆桌的,把大圆桌桌面直径看作单位“1”,单位“1”未知,用小圆桌桌面直径除以,求出大圆桌桌面直径;
根据圆的面积公式S=πr2,用大圆桌桌面的面积减去小圆桌桌面的面积即可。
【详解】大圆桌的直径:
1.6÷
=1.6×
=2(米)
大圆桌的面积比小圆桌大:
3.14×(2÷2)2-3.14×(1.6÷2)2
=3.14×1-3.14×0.64
=3.14×(1-0.64)
=3.14×0.36
≈1.13(平方米)
答:大圆桌面积比小圆桌大约大1.13平方米。
【点睛】本题考查分数除法的意义及应用,圆的面积公式的运用。
26.(1)31.4米;
(2)32.97平方米
【分析】(1)已知栅栏呈半圆形,半径是10米。根据圆的周长公式,求出半径为10米的圆的周长,然后再除以2即可得栅栏的长度;
(2)如果直径增加2米,则现在的半径变为(10+2÷2)米,然后根据圆的面积公式,求出现在鸡舍的面积和原来鸡舍的面积,再相减即可得鸡舍的面积增加了多少。
【详解】(1)3.14×10×2÷2
=62.8÷2
=31.4(米)
答:修这个鸡舍需要31.4米长的栅栏。
(2)10+2÷2
=10+1
=11(米)
3.14×11×11÷2-3.14×10×10÷2
=189.97-157
=32.97(平方米)
答:鸡舍的面积增加了32.97平方米。
【点睛】本题考查了圆的周长公式和面积公式,需要明确鸡舍的栅栏长度为圆周长的一半,鸡舍的面积为圆面积的一半。
27.50.24平方米
【分析】先求出圆形花园内圆的半径,即6÷2=3米,再加上环宽1米,就是外圆的半径,再利用圆的面积公式:即可得解。
【详解】6÷2=3(米)
3+1=4(米)
3.14×42
=3.14×16
=50.24(平方米)
答:这块场地占地面积是50.24平方米。
【点睛】此题的解题关键是掌握圆的面积的计算方法。注意此题不是求圆环的面积,而是求大圆的面积。
28.122.46平方米
【分析】内圆的半径为5米,增加了3米,则外圆的半径为(5+3)米,求增加的面积实际是求圆环的面积,利用圆环的面积公式:,代入数据,即可求出花坛的占地面积比原来多了多少平方米。
【详解】5+3=8(米)
3.14×(82-52)
=3.14×(64-25)
=3.14×39
=122.46(平方米)
答:这时花坛的占地面积比原来多了122.46平方米。
【点睛】此题的解题关键是理解增加的面积实际是在求圆环的面积,再利用圆环的面积计算方法求解。
29.314米
【分析】根据圆的周长公式:C=,代入直径求出圆的周长,因为圆属于封闭路线,用圆的周长除以馈源支撑塔的数量,即可求出每两座馈源支撑塔之间的距离。
【详解】3.14×600÷6=314(米)
答:每两座馈源支撑塔之间的距离是314米。
【点睛】此题的解题关键是结合圆的周长公式和植树问题中的处理方法,参照实际情况,列出算式,解决问题。
30.62.8米
【分析】相遇时间=相遇路程÷速度和,再根据猫每分钟比老鼠多走12.56米,乘相遇时间,求出当猫和老鼠第一次相遇时,猫比老鼠多走了多少米即可。
【详解】
(分钟)
(21.98-9.41)×5
=12.56×5
=62.8(米)
答:猫和老鼠第一次相遇时,猫比老鼠多走了62.8米。
【点睛】本题考查相遇问题、圆的周长,解答本题的关键是掌握相遇问题中的数量关系。
答案第1页,共2页
答案第1页,共2页
一、选择题(满分16分)
1.大圆与小圆的半径的比是3∶2,下面选项中错误的是( )。
A.它们的直径的比是3∶2 B.它们的周长的比是3∶2
C.它们的面积的比是3∶2 D.它们的面积的比是9∶4
2.圆的半径扩大到原来的5倍,圆的面积扩大到原来的( )。
A.5倍 B.10倍 C.25倍 D.无法确定
3.画圆时,圆的周长为31.4cm,那么圆规两脚尖的距离为( )。
A.1cm B.2.5cm C.5cm D.10cm
4.一个圆形蓄水池的周长是25.12m。它的占地面积是( )m2。
A.200.96 B.50.24 C.25.12
5.如下图所示,大半圆面积与小半圆面积的最简整数比是( )。
A.1∶1 B.2∶1 C.4∶1 D.1∶4
6.左图中长方形的面积是6cm2,那么半圆的面积是( )。
A.4.71 B.9.42 C.5
7.如下图,大圆直径2cm,小圆贴着大圆的内侧从P点开始按箭头所指方向滚动,小圆至少需要滚动( )周才能回到P点。
A.2 B.3 C.4
8.圆规两脚之间的距离如图床示,用此时的圆规所画出的圆的周长是( )cm。
A.3π B.4π C.6π
二、填空题(满分16分)
9.下图中长方形和圆的面积相等,长方形的长是6.28cm,则阴影部分的面积是( )cm2。
10.在一张长10cm,宽6cm的长方形纸片上画一个最大的半圆,这个半圆的周长是( )cm。
11.用一根31.4米的铁丝弯成一个圆形铁圈,铁圈的直径是( ),面积是( )。
12.一个圆的周长是31.4分米,它的面积是( )平方分米。
13.把一个圆平均分成若干(偶数)等份,然后剪开,拼成一个近似的长方形,这个长方形的长近似于( ),宽近似于( )。
14.如果把一个圆缩小,其周长由原来的31.4厘米变成15.7厘米,那么它的面积就变成原来的( )。
15.花园小区修建一个半径是4米的圆形花坛,在花坛周围又修建了一条1米宽的小路,这条小路的面积是( )平方米。
16.如图中圆的面积是,平行四边形的面积是________,三角形的面积是________。
三、判断题(满分8分)
17.甲乙两个圆的半径比是2∶9,它们的周长比也是2∶9。( )
18.半圆、正方形、长方形与平行四边形都是轴对称图形。( )
19.周长相等的两个圆,面积一定相等。( )
20.如图中正方形的面积是6.25cm2,则这个圆的面积是19.625cm2。( )
四、图形计算题(满分6分)
21.(6分)看图求出阴影部分的面积。(单位:厘米)
五、作图题(满分6分)
22.(6分)画出下列图形的对称轴。(有几条就画几条)
六、解答题(满分48分)
23.(6分)用一个边长6.28米的正方形铁丝框,重新围成一个圆,这个圆的面积是多少平方米?
24.(6分)一辆自行车车轮的外直径为72cm,王帆骑这辆自行车通过一座长2260.8m的大桥,如果期间车轮平均每分钟转100圈,那么他通过这座大桥需要几分钟?
25.(6分)餐厅有两种圆桌。小圆桌桌面直径是1.6米,是大圆桌的。大圆桌面积比小圆桌大约大多少平方米?(得数保留两位小数)
26.(6分)一个鸡舍依墙而建,呈半圆形,半径是10米。
(1)修这个鸡舍需要多长的栅栏?
(2)如果要扩建这个鸡舍,把它的直径增加2米。鸡舍的面积增加了多少?
27.(6分)学校要修建一个直径是6米的圆形花园,花园外留出1米宽的小路。这块场地占地面积是多少?
28.(6分)一个圆形花坛的半径是5米,现在要扩建花坛,将半径增加了3米,这时花坛的占地面积比原来多了多少平方米?
29.(6分)坐落于贵州的“天厦”射电望远惶外侧,直径600米的圆周上建造均匀布置的6座不同高度的馈源支撑塔,以及相关的塔基础、附属设施、防雷接地等。你能算出每两座馈源支撑塔之间的距离是多少吗?
30.(6分)猫和老鼠在一个直径是50米的圆周上的同一地点向相反方向运动,猫每分钟走21.98米,老鼠每分钟走9.42米。当猫和老鼠第一次相遇时,猫比老鼠多走了多少米?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【分析】根据圆的半径比与直径比、周长比相等,面积比等于半径的平方比;据此判断即可。
【详解】大圆与小圆的半径的比是3∶2,所以它们的直径的比是3∶2,它们的周长的比是3∶2,它们的面积比是9∶4。
故答案为:C
【点睛】本题主要考查了圆的半径比、直径比、周长比与面积比的关系及应用。
2.C
【分析】假设出原来圆的半径,利用“”分别求出原来圆的面积和现在圆的面积,最后求出圆的面积扩大的倍数,据此解答。
【详解】假设原来圆的半径为2。
原来圆的面积:
现在圆的面积:
=
=
÷=25
所以,圆的面积扩大到原来的25倍。
故答案为:C
【点睛】掌握圆的面积计算公式是解答题目的关键。
3.C
【分析】画圆时,圆规两脚尖的距离是半径,根据圆的半径=周长÷π÷2,列式计算即可。
【详解】31.4÷3.14÷2=5(cm)
圆规两脚尖的距离为5cm。
故答案为:C
【点睛】关键是熟悉画圆的方法,掌握并灵活运用圆的周长公式。
4.B
【分析】根据圆的周长公式:C=2πr,据此求出圆的半径,再根据圆的面积公式:S=πr2,据此计算即可。
【详解】25.12÷3.14÷2
=8÷2
=4(m)
3.14×42=50.24(m2)
则它的占地面积是50.24m2。
故答案为:B
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
5.C
【分析】根据圆的面积公式S=πr2,代入数据,分别求出大半圆和小半圆的面积,再写出对应的比,化简即可。
【详解】大半圆的面积:3.14×22÷2
=3.14×4÷2
=12.56÷2
=6.28
小半圆的面积:3.14×(2÷2)2÷2
=3.14×1÷2
=3.14÷2
=1.57
6.28∶1.57
=(6.28×100÷157)∶(1.57×100÷157)
=(628÷157)∶(157÷157)
=4∶1
故答案为:C
【点睛】此题主要考查了圆的面积公式的应用,注意因为此题是求两个数的比,不是求具体的数,所以在利用公式时带着π也可以。
6.A
【分析】长方形的长等于圆的直径,宽等于圆的半径,假设圆的半径为r,直径为2r,利用长方形的面积公式,代入求出r2,根据圆的面积公式:S=,代入r2的值,再除以2,即可求出半圆的面积。
【详解】假设圆的半径为r,则直径为2r,
r×2r=6
解:2r2=6
r2=6÷2
r2=3
半圆的面积:
=
=4.71(cm2)
故答案为:A
【点睛】此题的解题关键是利用长方形和圆之间的关系,灵活运用长方形和圆的面积公式,解决实际的问题。
7.A
【分析】根据圆的周长公式C=πd,小圆的直径等于大圆的半径,也就是大圆直径是小圆直径的2倍,因为圆周率是一定的,所以大小圆周长的比等于大小圆直径的比,小圆滚动的周数等于大圆周长是小圆周长的倍数,据此解答即可。
【详解】因为大圆直径是小圆直径的2倍,所以大圆周长是小圆周长的2倍;
故答案为:A
【点睛】此题主要考查圆的周长公式的灵活运用,关键是明确:大小圆周长的比等于大小圆直径的比。
8.B
【分析】圆规的两脚之间的距离就是所画圆的半径,根据直尺上的刻度求出圆的半径,再利用圆的周长公式:C=,代入即可求出所画出的圆的周长。
【详解】3-1=2(cm)
2×π×2=4π(cm)
故答案为:B
【点睛】此题考查了圆的周长的计算应用,关键是明白:圆规的两脚之间的距离就是所画圆的半径。
9.9.42
【分析】长方形的长已知,长方形的宽与圆的半径相等,可以用r来表示,长方形面积=长×宽,圆的面积S=πr2,因为长方形和圆的面积相等,所以6.28×r=πr2,由此可求出圆的半径,阴影部分面积=长方形面积-圆的面积。
【详解】假设圆的半径为r,由分析可知:长方形和圆的面积相等,即6.28×r=πr2。
那么圆的半径为:
6.28÷3.14=2(cm)
阴影部分面积:
6.28×2-×3.14×2×2
=12.56-3.14
=9.42(cm2)
【点睛】本题主要考查圆的面积公式,求得圆的半径是解题的关键。
10.25.7
【分析】在一张长10cm,宽6cm的长方形纸片上画一个最大的半圆,这个半圆的直径最大是10cm,直径÷2=半径,根据半圆的周长=πr+d,列式解答即可。
【详解】10÷2=5(cm)
3.14×5+10
=15.7+10
=25.7(cm)
这个半圆的周长是25.7cm。
【点睛】关键是熟悉半圆的特征,掌握并灵活运用半圆周长公式。
11. 10米 78.5平方米
【分析】圆的周长公式为C=πd,则d=C÷π把圆的周长代入可以求出圆的直径,在通过圆的直径是半径的2倍,求出半径,再利用S=πr2求出这个圆的面积。
【详解】直径:31.4÷3.14=10(米)
半径:10÷2=5(米)
面积:3.14×52=78.5(平方米)
【点睛】熟记并灵活运用圆的周长和面积计算公式是解答题目的关键。
12.78.5
【分析】根据圆的周长公式:C=2πr,据此求出圆的半径;再根据圆的面积公式:S=πr2,据此代入数值进行计算即可求出它的面积。
【详解】31.4÷3.14÷2
=10÷2
=5(分米)
3.14×52=78.5(平方分米)
则它的面积是78.5平方分米。
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
13. 圆周长的一半 圆的半径
【分析】根据圆面积公式推导的过程:把一个圆分成若干等份,拼成的图形近似于长方形,这个长方形的长相当于圆周长的一半,长方形的宽就是圆的半径,据此即可解答。
【详解】由分析可知:
把一个圆平均分成若干(偶数)等份,然后剪开,拼成一个近似的长方形,这个长方形的长近似于圆周长的一半,宽近似于圆的半径。
【点睛】此题考查的目的是理解掌握圆面积公式的推导过程。
14.
【分析】先根据“”求出圆的半径,再利用“”求出原来和现在圆的面积,最后用除法求出现在圆的面积占原来圆面积的分率,据此解答。
【详解】原来的半径:31.4÷3.14÷2
=10÷2
=5(厘米)
原来的面积:3.14×52=78.5(平方厘米)
现在的半径:15.7÷3.14÷2
=5÷2
=2.5(厘米)
现在的面积:3.14×2.52=19.625(平方厘米)
19.625÷78.5=
所以,它的面积就变成原来的。
【点睛】掌握圆的周长和面积的计算公式是解答题目的关键。
15.28.26
【分析】由题意可知,大圆的半径为(4+1)米,小圆的半径为4米,利用“”求出小路的面积,据此解答。
【详解】3.14×[(4+1)2-42]
=3.14×[52-42]
=3.14×[25-16]
=3.14×9
=28.26(平方米)
所以,这条小路的面积是28.26平方米。
【点睛】掌握环形的面积计算公式是解答题目的关键。
16. 24 21
【分析】观察图形可知,三角形和平行四边形的高相当于圆的直径,根据圆的面积公式:S=πr2,据此求出圆的半径,进而求出圆的直径,也就是三角形和平行四边形的高,再根据三角形的面积公式:S=ah÷2,平行四边形的面积公式:S=ah,代入数据计算即可求解。
【详解】28.26÷3.14=9(cm2)
因为3×3=9(cm2),所以圆的半径是3cm。
直径是3×2=6(cm)
7×6÷2
=42÷2
=21(cm2)
4×6=24(cm2)
则平行四边形的面积是24,三角形的面积是21。
【点睛】本题考查三角形、平行四边形和圆的面积,求出圆的半径是解题的关键。
17.√
【分析】根据甲乙两个圆的半径比是2∶9,设甲圆的半径为2r,则乙圆的半径为9r,代入圆的周长公式,表示出各自的周长,再利用比的意义即可求解。
【详解】解:设甲圆的半径为2r,则乙圆的半径为9r,
甲圆的周长=2×π×2r=4πr
乙圆的周长=2×π×9r=18πr
4πr∶18πr
=4∶18
=2∶9
即它们的周长比也是2∶9。
故答案为:√
【点睛】此题主要考查圆的周长的计算方法的灵活应用。
18.×
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可。
【详解】
如上图,半圆、正方形、长方形都是轴对称成图形,有对称轴,平行四边形不是轴对称图形。所以原说法错误。
故答案为:×
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
19.√
【分析】因为半径决定圆的大小,如果两个圆的周长相等,也就是两个圆的半径相等,那么两个圆的面积一定相等。据此判断。
【详解】周长相等的两个圆,面积一定相等。这种说法是正确的。
故答案为:√
【点睛】此题考查的目的是理解掌握圆的周长、面积的意义及应用。关键是明确:半径决定圆的大小。
20.√
【分析】根据题意知:圆的半径等于则正方形的边长,正方形的面积等于圆的半径平方,再根据圆的面积公式S=πr2即可求出圆的面积,由此进行判断。
【详解】3.14×6.25=19.625(cm2)
故答案为:√
【点睛】理解正方形的面积等于圆的半径平方,再代入圆的面积公式是解答本题的关键。
21.13.76平方厘米;65.94平方厘米
【分析】(1)空白部分的面积占整个圆面积的,阴影部分的面积=正方形的面积-圆的面积;
(2)阴影部分是一个圆环,圆环的面积计算公式为“”,把图中数据代入公式计算,据此解答。
【详解】(1)8×8-×82×3.14
=64-16×3.14
=64-50.24
=13.76(平方厘米)
所以,阴影部分的面积是13.76平方厘米。
(2)3.14×(52-22)
=3.14×21
=65.94(平方厘米)
所以,阴影部分的面积是65.94平方厘米。
22.见详解
【分析】如果将一个图形沿着一条直线对折,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。画对称轴时要用虚线。
第一个图形是由左、右2个大小相同的圆相切组成的,可以横着画1条对称轴,也可以竖着画一条对称轴,因此它有2条对称轴。
第二个图形是由左、右2个大小相同的圆相交组成的,可以横着画1条对称轴,也可以竖着画一条对称轴,因此它有2条对称轴。
第三个图形是由3个大小相同的圆组成的,把其中任意1个圆的圆心和另外2个圆的相交处相连并延长,都可以画出对称轴,因此它有3条对称轴。
【详解】如图。
【点睛】找组合图形的对称轴时,要把这些图形看作一个整体,仔细观察,发现对称轴的位置。
23.50.24平方米
【分析】先根据“正方形的周长=边长×4”求出铁丝的总长度,圆的周长等于铁丝的总长度,根据“”求出圆的半径,最后利用“”求出这个圆的面积,据此解答。
【详解】半径:6.28×4÷3.14÷2
=(6.28÷3.14)×(4÷2)
=2×2
=4(米)
面积:3.14×42=50.24(平方米)
答:这个圆的面积是50.24平方米。
【点睛】掌握圆的周长和面积计算公式是解答题目的关键。
24.10分钟
【分析】根据圆的周长=πd,求出车轮转一圈行进的距离,车轮周长×每分钟转动圈数=每分钟行驶距离,统一单位,根据时间=路程÷速度,列式解答即可。
【详解】3.14×72×100=22608(厘米)=226.08(米)
2260.8÷226.08=10(分钟)
答:他通过这座大桥需要10分钟。
【点睛】关键是掌握圆的周长公式,理解速度、时间、路程之间的关系。
25.1.13平方米
【分析】根据题意,小圆桌桌面直径是大圆桌的,把大圆桌桌面直径看作单位“1”,单位“1”未知,用小圆桌桌面直径除以,求出大圆桌桌面直径;
根据圆的面积公式S=πr2,用大圆桌桌面的面积减去小圆桌桌面的面积即可。
【详解】大圆桌的直径:
1.6÷
=1.6×
=2(米)
大圆桌的面积比小圆桌大:
3.14×(2÷2)2-3.14×(1.6÷2)2
=3.14×1-3.14×0.64
=3.14×(1-0.64)
=3.14×0.36
≈1.13(平方米)
答:大圆桌面积比小圆桌大约大1.13平方米。
【点睛】本题考查分数除法的意义及应用,圆的面积公式的运用。
26.(1)31.4米;
(2)32.97平方米
【分析】(1)已知栅栏呈半圆形,半径是10米。根据圆的周长公式,求出半径为10米的圆的周长,然后再除以2即可得栅栏的长度;
(2)如果直径增加2米,则现在的半径变为(10+2÷2)米,然后根据圆的面积公式,求出现在鸡舍的面积和原来鸡舍的面积,再相减即可得鸡舍的面积增加了多少。
【详解】(1)3.14×10×2÷2
=62.8÷2
=31.4(米)
答:修这个鸡舍需要31.4米长的栅栏。
(2)10+2÷2
=10+1
=11(米)
3.14×11×11÷2-3.14×10×10÷2
=189.97-157
=32.97(平方米)
答:鸡舍的面积增加了32.97平方米。
【点睛】本题考查了圆的周长公式和面积公式,需要明确鸡舍的栅栏长度为圆周长的一半,鸡舍的面积为圆面积的一半。
27.50.24平方米
【分析】先求出圆形花园内圆的半径,即6÷2=3米,再加上环宽1米,就是外圆的半径,再利用圆的面积公式:即可得解。
【详解】6÷2=3(米)
3+1=4(米)
3.14×42
=3.14×16
=50.24(平方米)
答:这块场地占地面积是50.24平方米。
【点睛】此题的解题关键是掌握圆的面积的计算方法。注意此题不是求圆环的面积,而是求大圆的面积。
28.122.46平方米
【分析】内圆的半径为5米,增加了3米,则外圆的半径为(5+3)米,求增加的面积实际是求圆环的面积,利用圆环的面积公式:,代入数据,即可求出花坛的占地面积比原来多了多少平方米。
【详解】5+3=8(米)
3.14×(82-52)
=3.14×(64-25)
=3.14×39
=122.46(平方米)
答:这时花坛的占地面积比原来多了122.46平方米。
【点睛】此题的解题关键是理解增加的面积实际是在求圆环的面积,再利用圆环的面积计算方法求解。
29.314米
【分析】根据圆的周长公式:C=,代入直径求出圆的周长,因为圆属于封闭路线,用圆的周长除以馈源支撑塔的数量,即可求出每两座馈源支撑塔之间的距离。
【详解】3.14×600÷6=314(米)
答:每两座馈源支撑塔之间的距离是314米。
【点睛】此题的解题关键是结合圆的周长公式和植树问题中的处理方法,参照实际情况,列出算式,解决问题。
30.62.8米
【分析】相遇时间=相遇路程÷速度和,再根据猫每分钟比老鼠多走12.56米,乘相遇时间,求出当猫和老鼠第一次相遇时,猫比老鼠多走了多少米即可。
【详解】
(分钟)
(21.98-9.41)×5
=12.56×5
=62.8(米)
答:猫和老鼠第一次相遇时,猫比老鼠多走了62.8米。
【点睛】本题考查相遇问题、圆的周长,解答本题的关键是掌握相遇问题中的数量关系。
答案第1页,共2页
答案第1页,共2页
