27.2.1相似三角形的判定(第3课时)[下学期]
文档属性
| 名称 | 27.2.1相似三角形的判定(第3课时)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 223.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-17 08:09:00 | ||
图片预览



文档简介
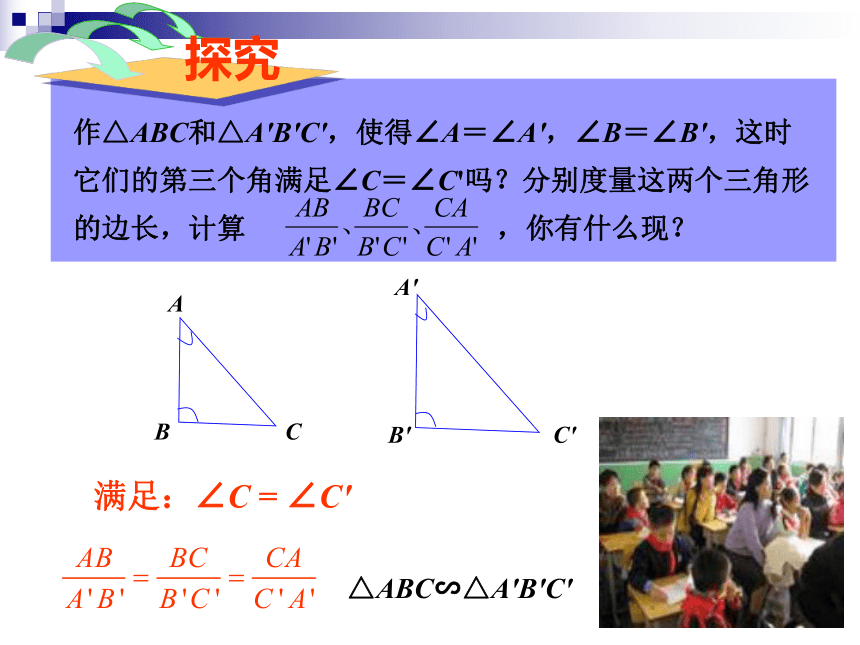
课件9张PPT。27.2.1 相似三角形的判定(第3课时)义务教育课程标准实验教科书九年级 上册人民教育出版社 观察两副三角尺如图,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.一般地,如果两个三角形有两组对应角相等,它们一定相似吗?观 察作△ABC和△A'B'C',使得∠A=∠A',∠B=∠B',这时它们的第三个角满足∠C=∠C'吗?分别度量这两个三角形的边长,计算 ,你有什么现?满足:∠C = ∠C'△ABC∽△A'B'C' 把你的结果与邻座的同学比较,你们的结论一样吗?
△ABC和△A'B'C'相似吗?一样△ABC和△A'B'C'相似得到判定两个三角形相似的又一个简便方法:如图,已知△ABC和△A'B'C'中,∠A=∠A', ∠B=∠B',
求证: △ABC∽△A'B'C'证明:在△ABC的边AB(或延长线)上,截取AD=A'B',过点D
作DE//BC,交AC于点E,则有△ADE∽△ABC∵∠ADE=∠B, ∠B=∠B'∴∠ADE=∠B'又∵∠A=∠A',AD=A'B'∴△ADE≌△A'B'C'∴△A'B'C'∽△ABC例2 如图,弦AB和CD相交于⊙O内一点P,求证PA·PB=PC·PD证明:连接AC、BD.∵ ∠A和∠D都是 所对的圆周角,∴ ∠A=∠D同理 ∠C=∠B∴ △PAC∽△PDB即 PA·PB=PC·PD·ABCDOP1. 底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.已知:等腰△ABC AB = AC 和等腰△A'B'C' ,A'B'=A'C'
且有∠B=∠B',
求证:△ABC∽△A'B'C'证明:∵等腰三角形 AB=AC ∴∠B=∠C∴△ABC∽△A'B'C' ∵等腰三角形 A'B'=A'C' ∴∠B'=∠C'∵∠B=∠B',∴∠C=∠C' 练 习已知:第腰△ABC 有AB=AC 和 △A'B'C' 有A'B'=A'C', 并且∠A=∠A', 求证:△ABC∽△A'B'C'证明:∵ △ABC中AB=AC,∠B =∠C∴ 2∠B =180°-∠A同理 △A'B'C'中A'B'=A'C',∠B' =∠C'∴ 2∠B' =180°-∠A'又 ∠A=∠A'∵ ∠B=∠B',∵ △ABC∽△A'B'C'2. 如图,Rt△ABC中,CD是斜边上的高,△ACD和△CBD都
和△ABC相似吗?证明你的结论.△ACD∽△ABC△CBD∽△ABC证明:∵∠ACB=∠ADC=90°又∠ A = ∠ A=90°∴ △ACD∽△ABC∵∠CDB=∠ACB=90°∠B = ∠B = 90°∴ △CBD∽△ABC
△ABC和△A'B'C'相似吗?一样△ABC和△A'B'C'相似得到判定两个三角形相似的又一个简便方法:如图,已知△ABC和△A'B'C'中,∠A=∠A', ∠B=∠B',
求证: △ABC∽△A'B'C'证明:在△ABC的边AB(或延长线)上,截取AD=A'B',过点D
作DE//BC,交AC于点E,则有△ADE∽△ABC∵∠ADE=∠B, ∠B=∠B'∴∠ADE=∠B'又∵∠A=∠A',AD=A'B'∴△ADE≌△A'B'C'∴△A'B'C'∽△ABC例2 如图,弦AB和CD相交于⊙O内一点P,求证PA·PB=PC·PD证明:连接AC、BD.∵ ∠A和∠D都是 所对的圆周角,∴ ∠A=∠D同理 ∠C=∠B∴ △PAC∽△PDB即 PA·PB=PC·PD·ABCDOP1. 底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.已知:等腰△ABC AB = AC 和等腰△A'B'C' ,A'B'=A'C'
且有∠B=∠B',
求证:△ABC∽△A'B'C'证明:∵等腰三角形 AB=AC ∴∠B=∠C∴△ABC∽△A'B'C' ∵等腰三角形 A'B'=A'C' ∴∠B'=∠C'∵∠B=∠B',∴∠C=∠C' 练 习已知:第腰△ABC 有AB=AC 和 △A'B'C' 有A'B'=A'C', 并且∠A=∠A', 求证:△ABC∽△A'B'C'证明:∵ △ABC中AB=AC,∠B =∠C∴ 2∠B =180°-∠A同理 △A'B'C'中A'B'=A'C',∠B' =∠C'∴ 2∠B' =180°-∠A'又 ∠A=∠A'∵ ∠B=∠B',∵ △ABC∽△A'B'C'2. 如图,Rt△ABC中,CD是斜边上的高,△ACD和△CBD都
和△ABC相似吗?证明你的结论.△ACD∽△ABC△CBD∽△ABC证明:∵∠ACB=∠ADC=90°又∠ A = ∠ A=90°∴ △ACD∽△ABC∵∠CDB=∠ACB=90°∠B = ∠B = 90°∴ △CBD∽△ABC
