角平分线的性质(练习课)
文档属性
| 名称 | 角平分线的性质(练习课) |

|
|
| 格式 | zip | ||
| 文件大小 | 154.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-29 00:00:00 | ||
图片预览

文档简介
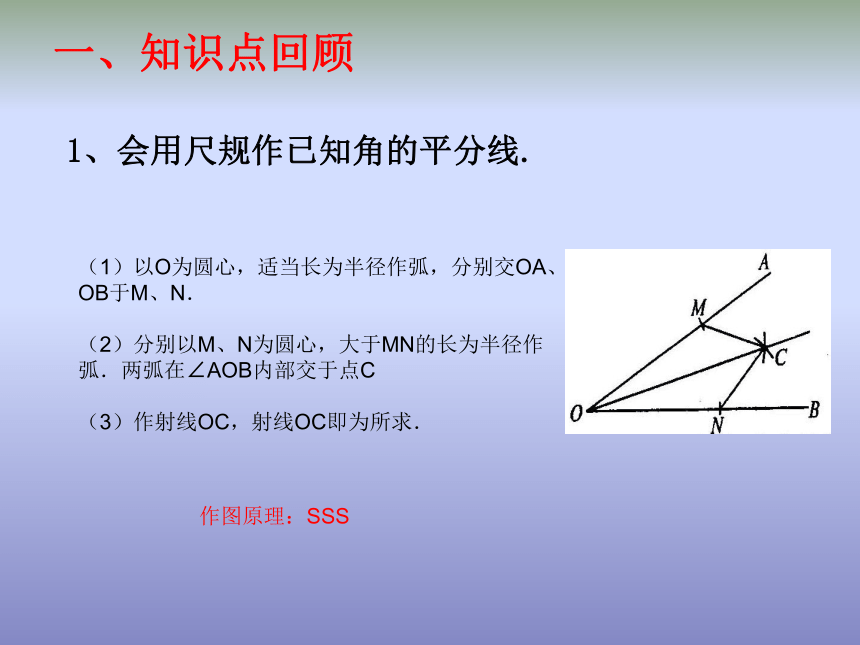
课件11张PPT。 角的平分线的性质 (练习课)1、会用尺规作已知角的平分线.一、知识点回顾(1)以O为圆心,适当长为半径作弧,分别交OA、 OB于M、N.
(2)分别以M、N为圆心,大于MN的长为半径作弧.两弧在∠AOB内部交于点C
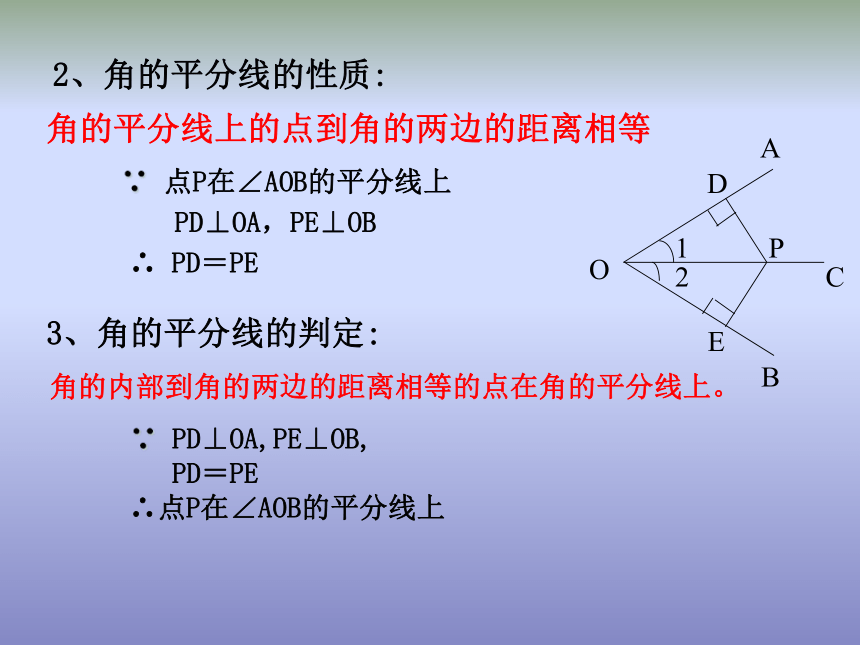
(3)作射线OC,射线OC即为所求.作图原理:SSS角的平分线上的点到角的两边的距离相等2、角的平分线的性质:PD⊥OA,PE⊥OB∵ 点P在∠AOB的平分线上∴ PD=PE角的内部到角的两边的距离相等的点在角的平分线上。3、角的平分线的判定:∵ PD⊥OA,PE⊥OB,
PD=PE
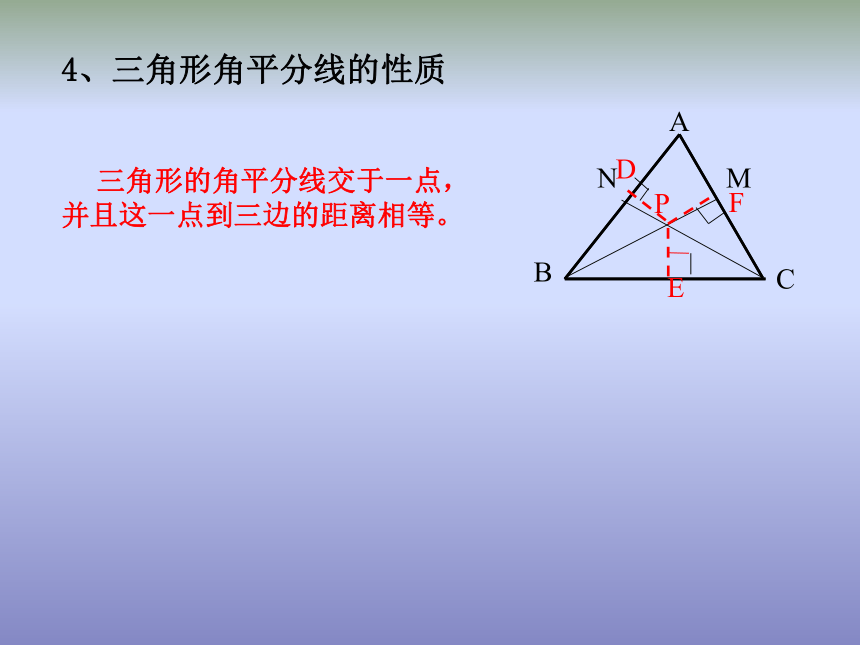
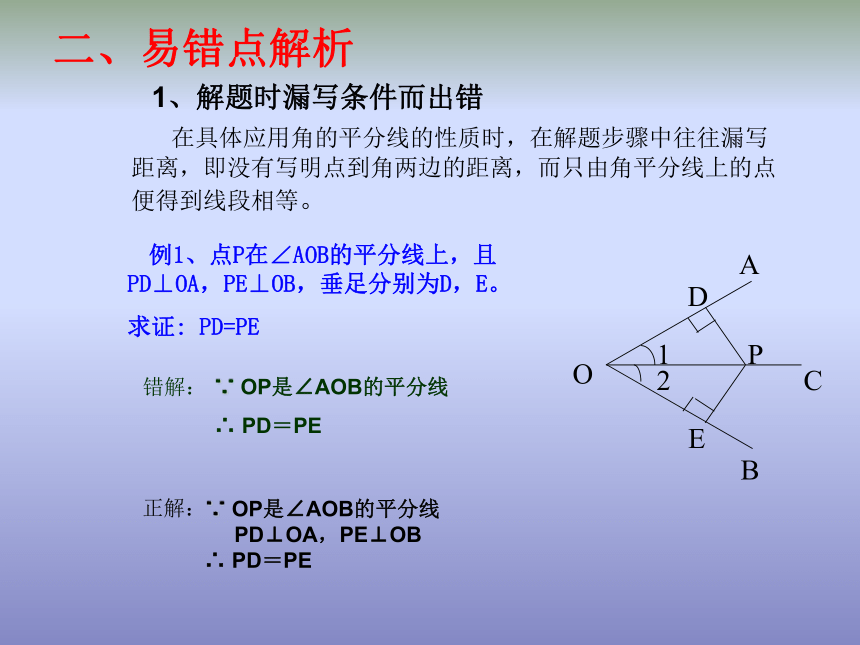
∴点P在∠AOB的平分线上4、三角形角平分线的性质 三角形的角平分线交于一点,并且这一点到三边的距离相等。二、易错点解析1、解题时漏写条件而出错 在具体应用角的平分线的性质时,在解题步骤中往往漏写距离,即没有写明点到角两边的距离,而只由角平分线上的点便得到线段相等。 例1、点P在∠AOB的平分线上,且PD⊥OA,PE⊥OB,垂足分别为D,E。
求证: PD=PE错解: ∵ OP是∠AOB的平分线
∴ PD=PE∵ OP是∠AOB的平分线
PD⊥OA,PE⊥OB
∴ PD=PE
正解:2、忽视条件而出错 角的平分线上的点到角的两边的距离是指这个点到角两边垂线段的长度,而不是过此点与角平分线垂直(或只相交)的直线与角两边相交得到的线段的长度。 例2、点P在∠AOB的平分线上,过点P的直线与OA,OB分别相交于D,E两点。问PD与PE相等吗?为什么?错解: ∵点P在∠AOB的平分线上,
∴ PD=PE 条件如果还加上“DE⊥OP”呢?3、解题方法选择出错 忽略角平分线的性质和判定的应用,机械的使用全等的知识来得到角相等或线段相等,使解题过程复杂化。 错解:∵点P在∠AOB的平分线上,
PD⊥OP PE⊥OP
∴ PD=PE 三、典型习题解析1、利用角平分线的性质证明线段之间的关系 例3、如图,BD平分∠ABC,AB=BC,点P在BD上, PM⊥AD,PN⊥CD,M,N为垂足。
求证:PM=PN2、利用角平分线的性质证明角之间的关系 例4、如图,点P为∠ABC平分线上的一点,点D和点E分别在AB和BC上,且PD=PE。
求证: ∠BDP+ ∠BEP= 180°3、角平分线的性质与判定的综合应用 例5、如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:AF平分∠DAE4、角平分线的性质实际应用 例6 、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建? 如果不限制在中间平地上修建,其他要求相同,那可以有几处可以修建?分别在哪里?四、考点热点链接 例6、如图,已知△ABC中,AB=7, ∠C= 90°,AC=BC,
AD平分∠ CAB,DE⊥AB于E,求△BDE的周长。
(2)分别以M、N为圆心,大于MN的长为半径作弧.两弧在∠AOB内部交于点C
(3)作射线OC,射线OC即为所求.作图原理:SSS角的平分线上的点到角的两边的距离相等2、角的平分线的性质:PD⊥OA,PE⊥OB∵ 点P在∠AOB的平分线上∴ PD=PE角的内部到角的两边的距离相等的点在角的平分线上。3、角的平分线的判定:∵ PD⊥OA,PE⊥OB,
PD=PE
∴点P在∠AOB的平分线上4、三角形角平分线的性质 三角形的角平分线交于一点,并且这一点到三边的距离相等。二、易错点解析1、解题时漏写条件而出错 在具体应用角的平分线的性质时,在解题步骤中往往漏写距离,即没有写明点到角两边的距离,而只由角平分线上的点便得到线段相等。 例1、点P在∠AOB的平分线上,且PD⊥OA,PE⊥OB,垂足分别为D,E。
求证: PD=PE错解: ∵ OP是∠AOB的平分线
∴ PD=PE∵ OP是∠AOB的平分线
PD⊥OA,PE⊥OB
∴ PD=PE
正解:2、忽视条件而出错 角的平分线上的点到角的两边的距离是指这个点到角两边垂线段的长度,而不是过此点与角平分线垂直(或只相交)的直线与角两边相交得到的线段的长度。 例2、点P在∠AOB的平分线上,过点P的直线与OA,OB分别相交于D,E两点。问PD与PE相等吗?为什么?错解: ∵点P在∠AOB的平分线上,
∴ PD=PE 条件如果还加上“DE⊥OP”呢?3、解题方法选择出错 忽略角平分线的性质和判定的应用,机械的使用全等的知识来得到角相等或线段相等,使解题过程复杂化。 错解:∵点P在∠AOB的平分线上,
PD⊥OP PE⊥OP
∴ PD=PE 三、典型习题解析1、利用角平分线的性质证明线段之间的关系 例3、如图,BD平分∠ABC,AB=BC,点P在BD上, PM⊥AD,PN⊥CD,M,N为垂足。
求证:PM=PN2、利用角平分线的性质证明角之间的关系 例4、如图,点P为∠ABC平分线上的一点,点D和点E分别在AB和BC上,且PD=PE。
求证: ∠BDP+ ∠BEP= 180°3、角平分线的性质与判定的综合应用 例5、如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:AF平分∠DAE4、角平分线的性质实际应用 例6 、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建? 如果不限制在中间平地上修建,其他要求相同,那可以有几处可以修建?分别在哪里?四、考点热点链接 例6、如图,已知△ABC中,AB=7, ∠C= 90°,AC=BC,
AD平分∠ CAB,DE⊥AB于E,求△BDE的周长。
