九年级数学沪科版下册试题 24.2.2 垂径定理 练习(含答案)
文档属性
| 名称 | 九年级数学沪科版下册试题 24.2.2 垂径定理 练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 817.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 14:24:55 | ||
图片预览




文档简介
24.2圆的基本性质--垂径定理
一、选择题
1.如图,的直径为26,弦的长为24,且,垂足为,则的长为
A.25 B.8 C.5 D.13
2.已知的半径为5,一条弦的弦心距为3,则此弦的长为
A.6 B.4 C.8 D.1
3.为内一点,,半径为5,则经过点的最短弦长为
A.5 B.6 C.8 D.10
4.如图的直径垂直于弦,垂足为,且,,则的半径为
A. B. C. D.
5.如图,的直径为10,弦的长为6,为弦上的动点,则线段长的取值范围是
A.3≦OP≦5 B. C.4≦OP≦5 D.
6.如图,在半径为5的中,半径弦于点,连接并延长交于点,连接、.若,则的长为
A. B.8 C. D.
7.如图,的半径为13,弦,是弦上的一个动点,不在取值范围内的是
A.4 B.5 C.12 D.13
8.如图,是的直径,弦于,连接,过点作于,若,,则的长度是
A. B. C. D.
9.的直径为20,圆上两点、距离为16,上一动点到直线距离的最大值为
A.16 B.18 C.24 D.32
10.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心为圆心的圆,如图2.已知圆心在水面上方,且被水面截得的弦长为6米,半径长为4米.若点为运行轨道的最低点,则点到弦所在直线的距离是
A.1米 B.米 C.2米 D.米
二、填空题
11.如图,是的一条弦,于点,交于点,连接.若,,则的半径为 .
12.如图,已知在半径为10的中,弦,,则的长为 .
13.已知的直径,是的弦,,垂足为点,若,则线段的长为 .
14.如图,是的直径,弦于点,,,则的半径 .
15.如图所示一个圆柱体容器内装入一些水,截面在圆心下方,若的直径为,水面宽,则水的最大深度为 .
16.小明很喜欢钻研问题,一次数学杨老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径,小明连接瓦片弧线两端,量的弧的中心到的距离,,很快求得圆形瓦片所在圆的半径为 .
17.如图是一种机械传动装置示意图,的半径为,点固定在上,连杆定长,点随着的转动在射线上运动.在一个停止状态时,与交于点,测得,,此时长为 .
18.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心为圆心,为半径的圆,且圆心在水面上方.若圆被水面截得的弦长为,则筒车工作时,盛水桶在水面以下的最大深度为 .
三、解答题
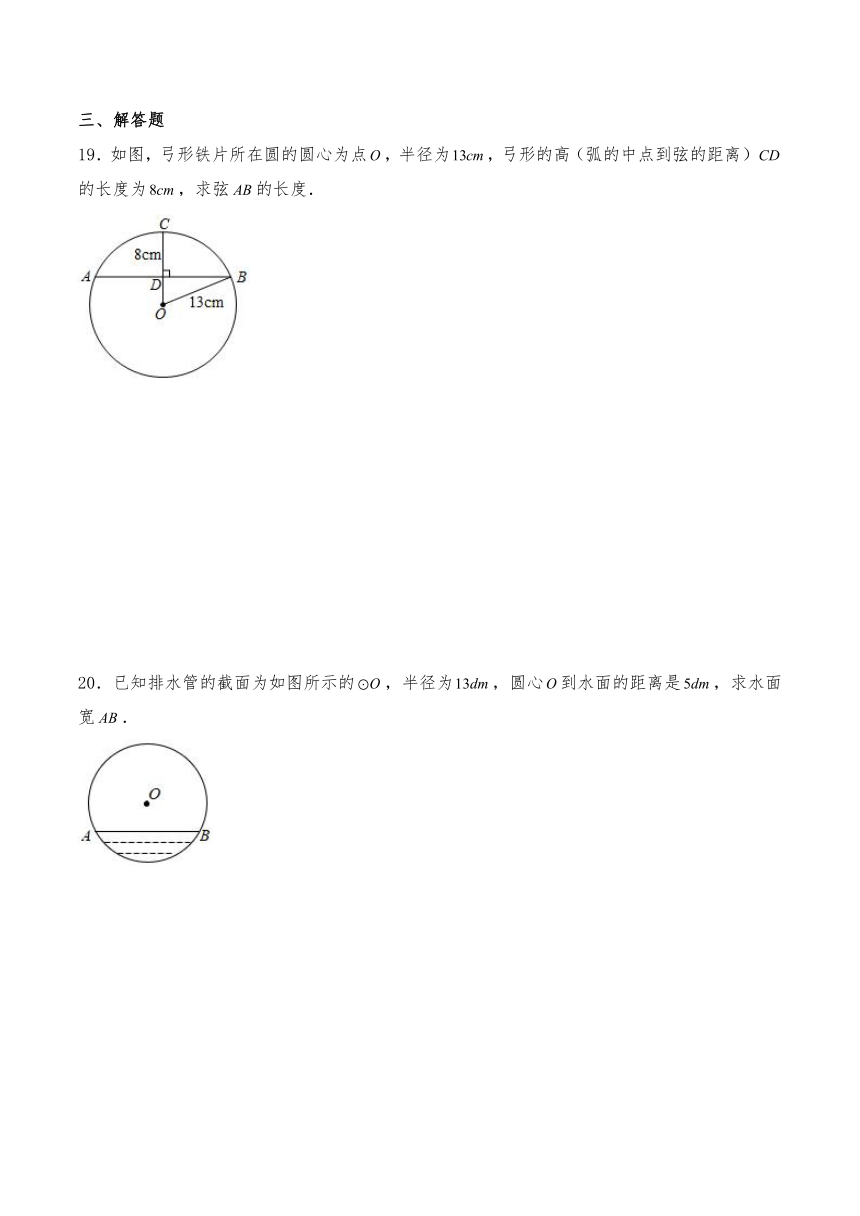
19.如图,弓形铁片所在圆的圆心为点,半径为,弓形的高(弧的中点到弦的距离)的长度为,求弦的长度.
20.已知排水管的截面为如图所示的,半径为,圆心到水面的距离是,求水面宽.
21.如图,有一座圆弧形拱桥,桥下水面宽度为,拱高为.
(1)求拱桥的半径;
(2)有一艘宽为的货船,船舱顶部为长方形,并高出水面,则此货船是否能顺利通过此圆弧形拱桥,并说明理由.
22.如图,某隧道的截面是一个半径为3.4米的半圆形,一辆宽3.2米的厢式卡车(截面是长方形)恰好能通过该隧道,则这辆卡车的高为多少米?
23.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端分米,为中点,为拱门最高点,圆心在线段上,分米,求拱门所在圆的半径.
24.如图所示,某地欲搭建一座圆弧型拱桥,跨度米,拱高米为的中点,为弧的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩支撑,求桥墩的高度.
答案
一、选择题
..........
二、填空题
11.2.5. 12.6. 13.9或1. 14..
15.12. 16.4. 17.. 18..
三、解答题
19.,
,
,,
,
,
.
20.如图,过点作于点,连接.
由垂径定理可知,,.
由勾股定理得,
所以.
21.(1)如图,连接,.
,
为中点,
,
.
又,
设,则.
在中,根据勾股定理得:,
解得.
(2),船舱顶部为长方形并高出水面,
,
,
在中,,
.
.
此货船能顺利通过这座拱桥.
22.过作于,
则,米,
由垂径定理得:(米,
在中,,米,米,由勾股定理得:(米,
即这辆卡车的高为3米.
23.连接,
过圆心,为的中点,
,
,为的中点,
,
设圆的半径为分米,则分米,
,
,
在中,,
,
(分米),
答:拱门所在圆的半径是15分米.
24.(1)设弧所在的圆心为,为弧的中点,于,延长经过点,设的半径为,
在中,,
,
解得;
(2)于,则,,
在中,,
,(米,
在离桥的一端4米处,桥墩高4米.
一、选择题
1.如图,的直径为26,弦的长为24,且,垂足为,则的长为
A.25 B.8 C.5 D.13
2.已知的半径为5,一条弦的弦心距为3,则此弦的长为
A.6 B.4 C.8 D.1
3.为内一点,,半径为5,则经过点的最短弦长为
A.5 B.6 C.8 D.10
4.如图的直径垂直于弦,垂足为,且,,则的半径为
A. B. C. D.
5.如图,的直径为10,弦的长为6,为弦上的动点,则线段长的取值范围是
A.3≦OP≦5 B. C.4≦OP≦5 D.
6.如图,在半径为5的中,半径弦于点,连接并延长交于点,连接、.若,则的长为
A. B.8 C. D.
7.如图,的半径为13,弦,是弦上的一个动点,不在取值范围内的是
A.4 B.5 C.12 D.13
8.如图,是的直径,弦于,连接,过点作于,若,,则的长度是
A. B. C. D.
9.的直径为20,圆上两点、距离为16,上一动点到直线距离的最大值为
A.16 B.18 C.24 D.32
10.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心为圆心的圆,如图2.已知圆心在水面上方,且被水面截得的弦长为6米,半径长为4米.若点为运行轨道的最低点,则点到弦所在直线的距离是
A.1米 B.米 C.2米 D.米
二、填空题
11.如图,是的一条弦,于点,交于点,连接.若,,则的半径为 .
12.如图,已知在半径为10的中,弦,,则的长为 .
13.已知的直径,是的弦,,垂足为点,若,则线段的长为 .
14.如图,是的直径,弦于点,,,则的半径 .
15.如图所示一个圆柱体容器内装入一些水,截面在圆心下方,若的直径为,水面宽,则水的最大深度为 .
16.小明很喜欢钻研问题,一次数学杨老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径,小明连接瓦片弧线两端,量的弧的中心到的距离,,很快求得圆形瓦片所在圆的半径为 .
17.如图是一种机械传动装置示意图,的半径为,点固定在上,连杆定长,点随着的转动在射线上运动.在一个停止状态时,与交于点,测得,,此时长为 .
18.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心为圆心,为半径的圆,且圆心在水面上方.若圆被水面截得的弦长为,则筒车工作时,盛水桶在水面以下的最大深度为 .
三、解答题
19.如图,弓形铁片所在圆的圆心为点,半径为,弓形的高(弧的中点到弦的距离)的长度为,求弦的长度.
20.已知排水管的截面为如图所示的,半径为,圆心到水面的距离是,求水面宽.
21.如图,有一座圆弧形拱桥,桥下水面宽度为,拱高为.
(1)求拱桥的半径;
(2)有一艘宽为的货船,船舱顶部为长方形,并高出水面,则此货船是否能顺利通过此圆弧形拱桥,并说明理由.
22.如图,某隧道的截面是一个半径为3.4米的半圆形,一辆宽3.2米的厢式卡车(截面是长方形)恰好能通过该隧道,则这辆卡车的高为多少米?
23.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端分米,为中点,为拱门最高点,圆心在线段上,分米,求拱门所在圆的半径.
24.如图所示,某地欲搭建一座圆弧型拱桥,跨度米,拱高米为的中点,为弧的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩支撑,求桥墩的高度.
答案
一、选择题
..........
二、填空题
11.2.5. 12.6. 13.9或1. 14..
15.12. 16.4. 17.. 18..
三、解答题
19.,
,
,,
,
,
.
20.如图,过点作于点,连接.
由垂径定理可知,,.
由勾股定理得,
所以.
21.(1)如图,连接,.
,
为中点,
,
.
又,
设,则.
在中,根据勾股定理得:,
解得.
(2),船舱顶部为长方形并高出水面,
,
,
在中,,
.
.
此货船能顺利通过这座拱桥.
22.过作于,
则,米,
由垂径定理得:(米,
在中,,米,米,由勾股定理得:(米,
即这辆卡车的高为3米.
23.连接,
过圆心,为的中点,
,
,为的中点,
,
设圆的半径为分米,则分米,
,
,
在中,,
,
(分米),
答:拱门所在圆的半径是15分米.
24.(1)设弧所在的圆心为,为弧的中点,于,延长经过点,设的半径为,
在中,,
,
解得;
(2)于,则,,
在中,,
,(米,
在离桥的一端4米处,桥墩高4米.
