九年级沪科版数学下册试题 24.2.4 圆的确定 练习(含答案)
文档属性
| 名称 | 九年级沪科版数学下册试题 24.2.4 圆的确定 练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 857.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 00:00:00 | ||
图片预览


文档简介
24.2圆的基本性质--圆的确定
一、选择题
1.经过不在同一直线上的三个点可以作圆的个数是
A.1 B.2 C.3 D.无数
2.下列关于圆的说法,正确的是
A.弦是直径,直径也是弦
B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴
D.过三点可以作一个圆
3.下列说法错误的是
A.已知圆心和半径可以作一个圆
B.经过一个已知点的圆能作无数个
C.经过两个已知点,的圆能作两个
D.经过不在同一直线上的三个点,,只能作一个圆
4.过、、三点能确定一个圆的条件是
①,,;
②,,;
③,,.
A.①② B.①②③ C.②③ D.①③
5.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是
A.① B.② C.③ D.④
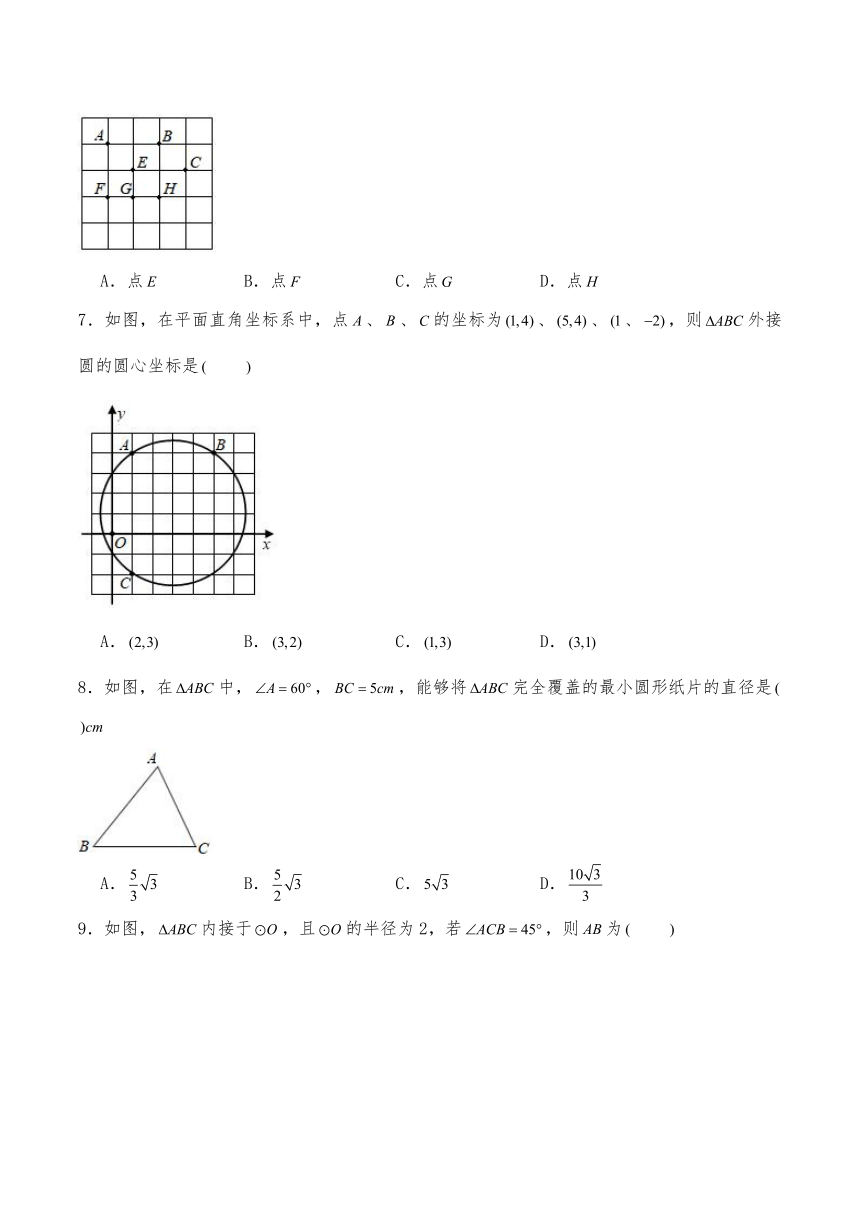
6.如图所示的正方形网格中,,,三点均在格点上,那么的外接圆圆心是
A.点 B.点 C.点 D.点
7.如图,在平面直角坐标系中,点、、的坐标为、、、,则外接圆的圆心坐标是
A. B. C. D.
8.如图,在中,,,能够将完全覆盖的最小圆形纸片的直径是
A. B. C. D.
9.如图,内接于,且的半径为2,若,则为
A.2 B. C.4 D.
10.如图,内接于,且圆心在边上,半径为8,点是弧的中点,分别连接,,若,则的长为
A. B.8 C.10 D.
二、填空题
11.已知某直角三角形的边长分别是、,则它的外接圆半径是 .
12.如图,内接于,,,于点,若的半径为4,则的长为 .
13.如图,是的外接圆,,,则的直径长等于 .
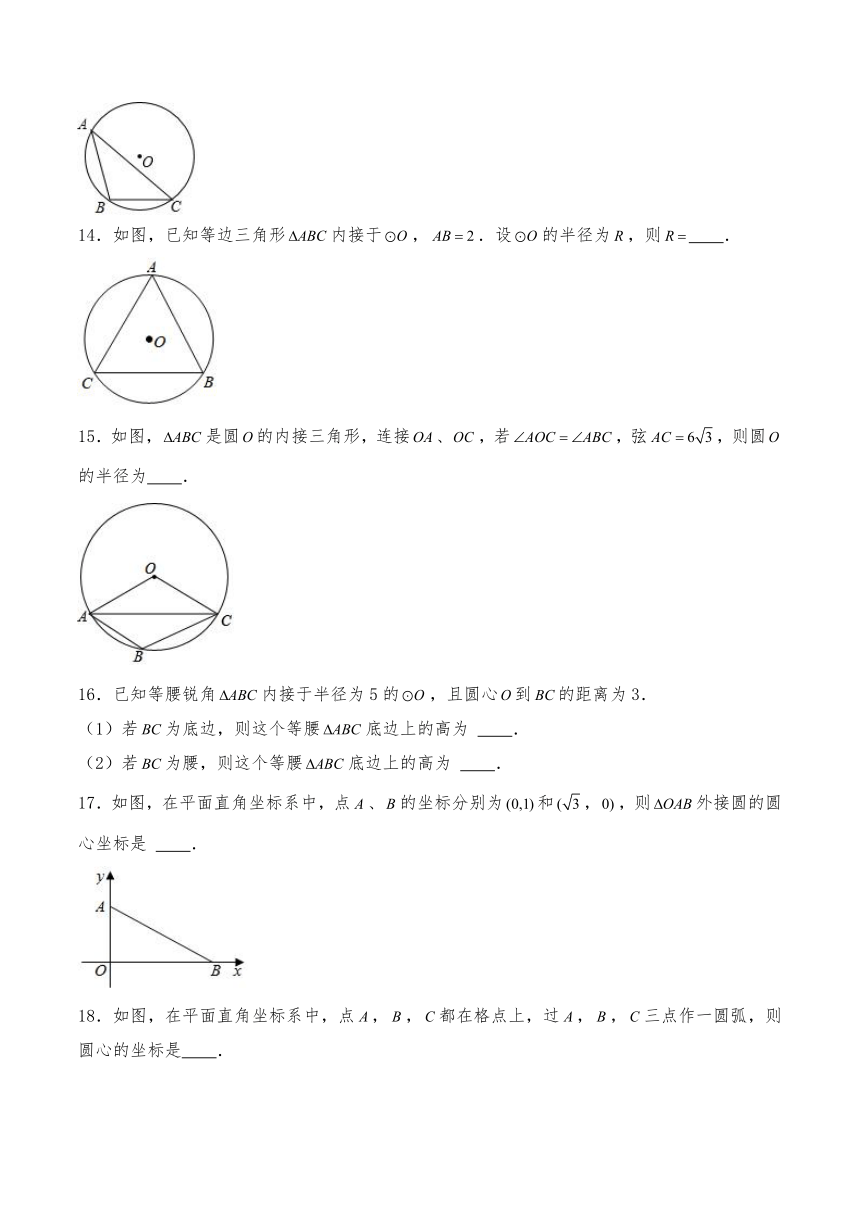
14.如图,已知等边三角形内接于,.设的半径为,则 .
15.如图,是圆的内接三角形,连接、,若,弦,则圆的半径为 .
16.已知等腰锐角内接于半径为5的,且圆心到的距离为3.
(1)若为底边,则这个等腰底边上的高为 .
(2)若为腰,则这个等腰底边上的高为 .
17.如图,在平面直角坐标系中,点、的坐标分别为和,,则外接圆的圆心坐标是 .
18.如图,在平面直角坐标系中,点,,都在格点上,过,,三点作一圆弧,则圆心的坐标是 .
三、解答题
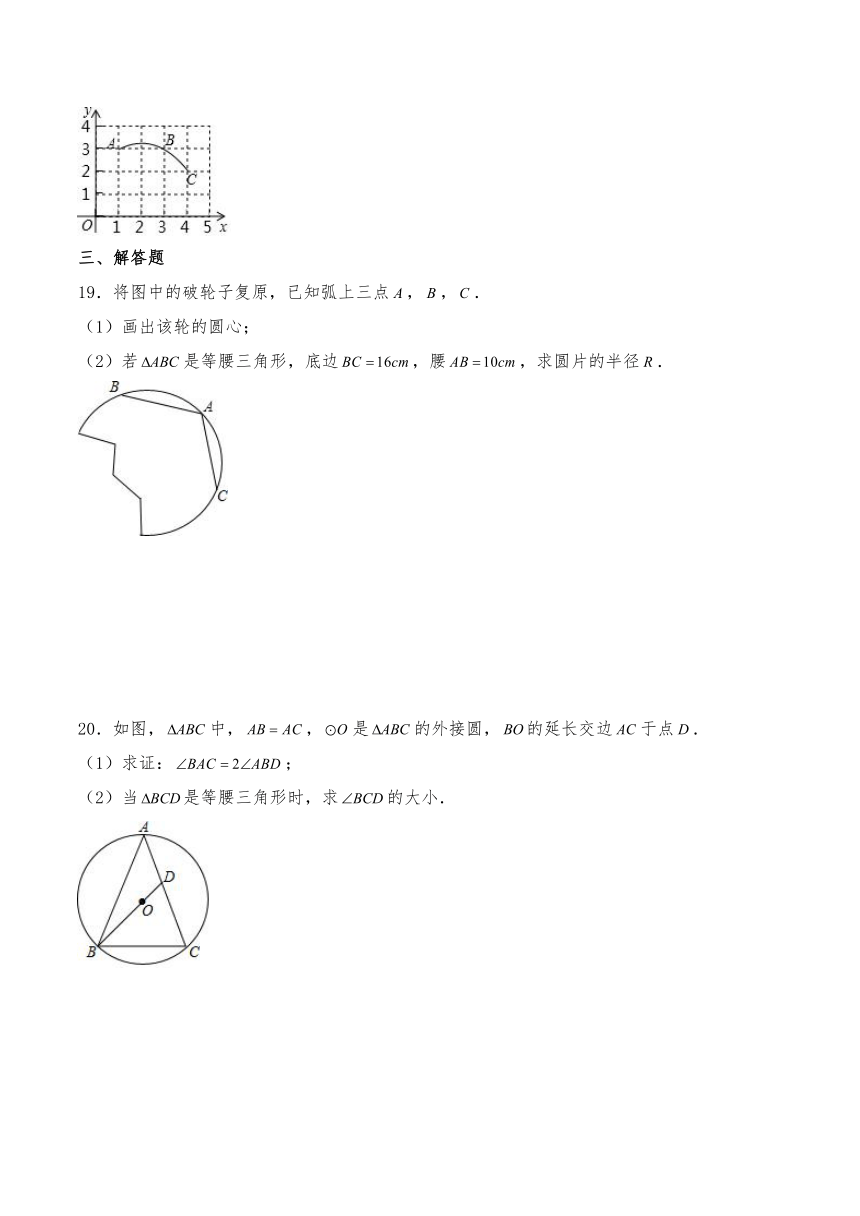
19.将图中的破轮子复原,已知弧上三点,,.
(1)画出该轮的圆心;
(2)若是等腰三角形,底边,腰,求圆片的半径.
20.如图,中,,是的外接圆,的延长交边于点.
(1)求证:;
(2)当是等腰三角形时,求的大小.
21.如图,是的外接圆,长为4,,联结并延长,交边于点,交于点,且为弧的中点.求:
(1)边的长;
(2)的半径.
22.如图,在平面直角坐标系中,、、.
(1)经过、、三点的圆弧所在圆的圆心的坐标为 ;
(2)这个圆的半径为 ;
(3)直接判断点与的位置关系.点在 (填内、外、上).
23.如图,内接于,于点,,为直径,的半径为2,连接.
(1)求的长;
(2)求证:.
24.如图,在中,,,,点从点开始以的速度沿向点运动,点从点开始以的速度沿向点运动,点、同时出发,当一个点到达终点时,另一个点也停止运动.
(1)2秒时,的面积是 ;
(2)求经过几秒,的面积是;
(3)试说明外接圆的半径能否是.
答案
一、选择题
..........
二、填空题
11.2.5或2. 12.. 13.4. 14..
15.6. 16.8; . 17.,. 18..
三、解答题
19.(1)如图所示:分别作弦和的垂直平分线交点即为所求的圆心;
(2)连接,,,交于.
,
,
,
,
设圆片的半径为,在中,,
,
解得:,
圆片的半径为.
20.(1)连接并延长交于,
,
弧弧,
过圆心,
垂直平分(平分弧的直径垂直平分弧所对的弦),
平分,
,
,
,
;
(2)设,
由(1)知,
,
是等腰三角形,
①若,
则,
,
,
在中,,
,
解得,
,
②若,则,
,
在中,,
,
,
,
综上所述,是等腰三角形,为或.
21.(1)点为的中点,为直径,
,
,
即垂直平分,
;
(2)连接,如图,
,
为等边三角形,
,
,
,
在中,,
,
,
即的半径为.
22.(1)如图,圆心的坐标为;
(2),,
,
即的半径为;
(3),,
,
,
点在内.
故答案为;;内.
23.(1)如图,连接,
于点,,
,
,
是的直径,
,
,
;
(2)证明:是的直径,
,
,
,
,
,
,
,
.
24.(1),,,
,
根据题意得,,,
,
;
故答案为;
(2)设经过秒,
根据题意得,,
解得,;
即经过1秒或3秒,的面积是;
(3)为直角三角形,,
为外接圆的直径,
假设外接圆的半径为,则,
设点运动的时间为秒,则,,
根据题意得,,
整理得,
△,
原方程没有实数解,
外接圆的半径不能是.
一、选择题
1.经过不在同一直线上的三个点可以作圆的个数是
A.1 B.2 C.3 D.无数
2.下列关于圆的说法,正确的是
A.弦是直径,直径也是弦
B.半圆是圆中最长的弧
C.圆的每一条直径所在的直线都是它的对称轴
D.过三点可以作一个圆
3.下列说法错误的是
A.已知圆心和半径可以作一个圆
B.经过一个已知点的圆能作无数个
C.经过两个已知点,的圆能作两个
D.经过不在同一直线上的三个点,,只能作一个圆
4.过、、三点能确定一个圆的条件是
①,,;
②,,;
③,,.
A.①② B.①②③ C.②③ D.①③
5.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是
A.① B.② C.③ D.④
6.如图所示的正方形网格中,,,三点均在格点上,那么的外接圆圆心是
A.点 B.点 C.点 D.点
7.如图,在平面直角坐标系中,点、、的坐标为、、、,则外接圆的圆心坐标是
A. B. C. D.
8.如图,在中,,,能够将完全覆盖的最小圆形纸片的直径是
A. B. C. D.
9.如图,内接于,且的半径为2,若,则为
A.2 B. C.4 D.
10.如图,内接于,且圆心在边上,半径为8,点是弧的中点,分别连接,,若,则的长为
A. B.8 C.10 D.
二、填空题
11.已知某直角三角形的边长分别是、,则它的外接圆半径是 .
12.如图,内接于,,,于点,若的半径为4,则的长为 .
13.如图,是的外接圆,,,则的直径长等于 .
14.如图,已知等边三角形内接于,.设的半径为,则 .
15.如图,是圆的内接三角形,连接、,若,弦,则圆的半径为 .
16.已知等腰锐角内接于半径为5的,且圆心到的距离为3.
(1)若为底边,则这个等腰底边上的高为 .
(2)若为腰,则这个等腰底边上的高为 .
17.如图,在平面直角坐标系中,点、的坐标分别为和,,则外接圆的圆心坐标是 .
18.如图,在平面直角坐标系中,点,,都在格点上,过,,三点作一圆弧,则圆心的坐标是 .
三、解答题
19.将图中的破轮子复原,已知弧上三点,,.
(1)画出该轮的圆心;
(2)若是等腰三角形,底边,腰,求圆片的半径.
20.如图,中,,是的外接圆,的延长交边于点.
(1)求证:;
(2)当是等腰三角形时,求的大小.
21.如图,是的外接圆,长为4,,联结并延长,交边于点,交于点,且为弧的中点.求:
(1)边的长;
(2)的半径.
22.如图,在平面直角坐标系中,、、.
(1)经过、、三点的圆弧所在圆的圆心的坐标为 ;
(2)这个圆的半径为 ;
(3)直接判断点与的位置关系.点在 (填内、外、上).
23.如图,内接于,于点,,为直径,的半径为2,连接.
(1)求的长;
(2)求证:.
24.如图,在中,,,,点从点开始以的速度沿向点运动,点从点开始以的速度沿向点运动,点、同时出发,当一个点到达终点时,另一个点也停止运动.
(1)2秒时,的面积是 ;
(2)求经过几秒,的面积是;
(3)试说明外接圆的半径能否是.
答案
一、选择题
..........
二、填空题
11.2.5或2. 12.. 13.4. 14..
15.6. 16.8; . 17.,. 18..
三、解答题
19.(1)如图所示:分别作弦和的垂直平分线交点即为所求的圆心;
(2)连接,,,交于.
,
,
,
,
设圆片的半径为,在中,,
,
解得:,
圆片的半径为.
20.(1)连接并延长交于,
,
弧弧,
过圆心,
垂直平分(平分弧的直径垂直平分弧所对的弦),
平分,
,
,
,
;
(2)设,
由(1)知,
,
是等腰三角形,
①若,
则,
,
,
在中,,
,
解得,
,
②若,则,
,
在中,,
,
,
,
综上所述,是等腰三角形,为或.
21.(1)点为的中点,为直径,
,
,
即垂直平分,
;
(2)连接,如图,
,
为等边三角形,
,
,
,
在中,,
,
,
即的半径为.
22.(1)如图,圆心的坐标为;
(2),,
,
即的半径为;
(3),,
,
,
点在内.
故答案为;;内.
23.(1)如图,连接,
于点,,
,
,
是的直径,
,
,
;
(2)证明:是的直径,
,
,
,
,
,
,
,
.
24.(1),,,
,
根据题意得,,,
,
;
故答案为;
(2)设经过秒,
根据题意得,,
解得,;
即经过1秒或3秒,的面积是;
(3)为直角三角形,,
为外接圆的直径,
假设外接圆的半径为,则,
设点运动的时间为秒,则,,
根据题意得,,
整理得,
△,
原方程没有实数解,
外接圆的半径不能是.
