九年级数学下册试题 24.6正多边形与圆-沪科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 24.6正多边形与圆-沪科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 906.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 16:30:40 | ||
图片预览

文档简介
24.6正多边形与圆
一、选择题
1.正六边形的边长为,则它的面积为
A. B. C. D.
2.一个圆的内接正六边形与内接正方形的边长之比为
A. B. C. D.
3.如图,正方形内接于,点在上,则的度数为
A. B. C. D.
4.如图,是正六边形的外接圆,点在上不与,重合),则的度数为
A.或 B.或 C. D.
5.在圆内接正六边形中,正六边形的边长为2,则这个正六边形的中心角和边心距分别是
A.,1 B., C., D.,2
6.如图,正方形内接于.点为上一点,连接、,若,,则的长为
A. B. C. D.
7.如图,在一张圆形纸片上剪下一个面积最大的正六边形纸片,它的边长是,的长度是
A. B. C. D.
8.如图,正五边形内接于,点为上一点(点与点,点不重合),连接,,,垂足为,则等于
A. B. C. D.
9.如图,与正六边形的边、分别交于点、,点为劣弧的中点.若,则的半径为
A.2 B. C. D.
10.如图,以正六边形的对角线为边,再作一个正六边形,若,则的长为
A.2 B. C.3 D.
二、填空题
11.两个全等的正方形如图放置,重叠部分为正八边形,且其各边长都为,每个内角均为,则正方形的边长为 .
12.如图,正方形内接于,的半径为6,则的长为 .
13.如图,边长为的正六边形内有两个三角形(数据如图),则 .
14.如图,在正六边形中,于相交于点,则值为 .
15.如图,要拧开一个边长为的正六边形螺料,扳手张开的开口至少为 .
16.如图,正方形和正六边形均内接于,连接;若线段恰好是的一个内接正边形的一条边,则 .
17.如图,正八边形内接于,若,则点到的距离为 .
18.如图,是正五边形的一条对角线,以为圆心,为半径画弧交于点,连接,则 .
三、解答题
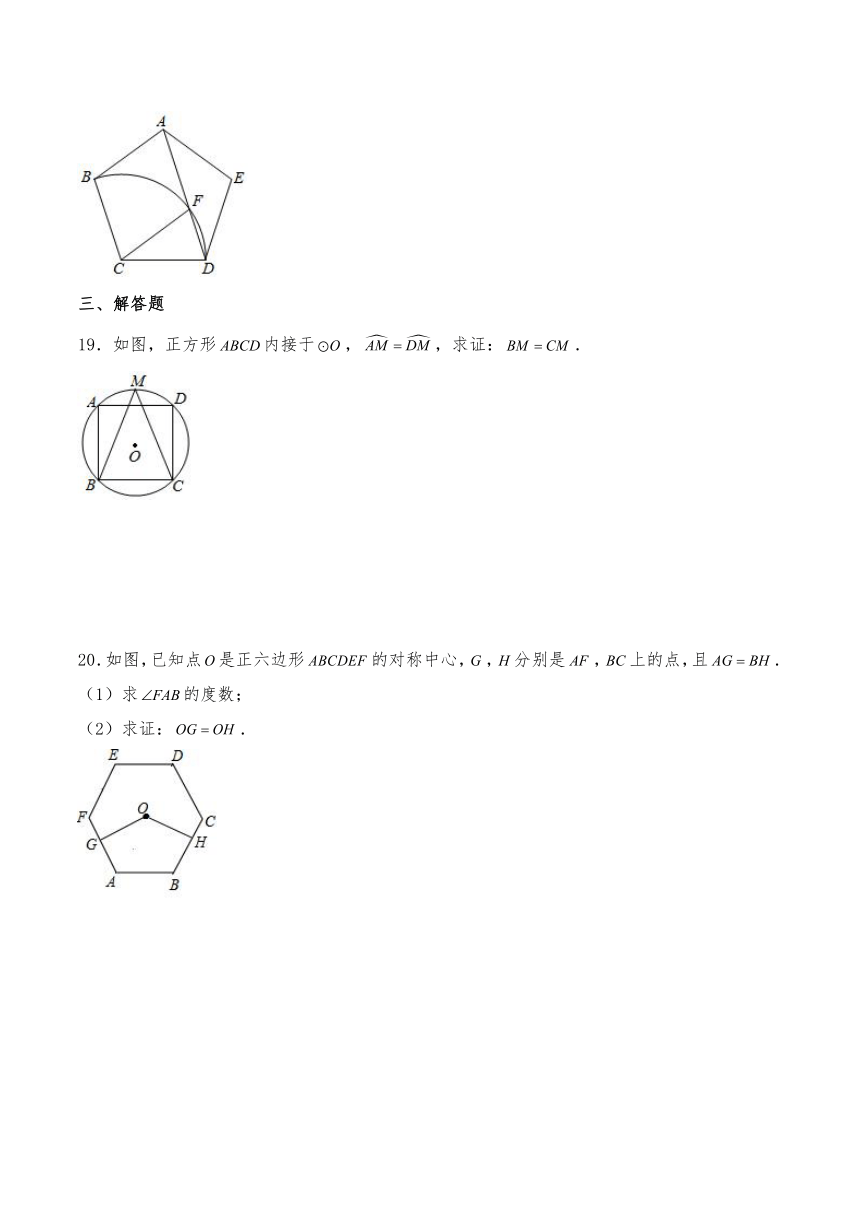
19.如图,正方形内接于,,求证:.
20.如图,已知点是正六边形的对称中心,,分别是,上的点,且.
(1)求的度数;
(2)求证:.
21.如图,,,,是上的四个点,.
(1)求证:是等边三角形.
(2)若的半径为2,求等边的边心距.
22.已知,正方形内接于,点是弧上一点.
(1)如图1,若点是弧的中点,求证:;
(2)如图2,若图中,求的值.
23.(1)已知:如图1,是的内接正三角形,点为劣弧上一动点.求证:;
(2)已知:如图2,四边形是的内接正方形,点为劣弧上一动点.求证:.
24.如图1,为等边三角形,图2为正方形,图3为正五边形,图4为正多边形.
(1)如图1当时,请求出的度数,并说明理由
(2)如图2,在正方形中,当时 ;如图3,在正五边形中,当时, ;
(3)如图4,在正边形中,当时,是否有什么规律?如果有请用含有的式子直接表示;如果没有规律,请说明理由.
答案
一、选择题
.. ........
二、填空题
11.. 12.. 13.5. 14.. 15..
16.12. 17.2. 18.72.
三、解答题
19.证明:四边形是正方形,
,
,
,
,即,
.
20.(1)解:六边形是正六边形,
;
(2)证明:连接、,
,
,
,
,
在和中,
,
.
21.(1)证明:在中,
与是对的圆周角,与是所对的圆周角,
,,
又,
,
为等边三角形;
(2)过作于,连接,
则,,
,
,
等边的边心距为1.
22.(1)证明:如图1,连接,
四边形是正方形,
,,
,,
,
点是弧的中点,
,
,
,
,
;
(2)解:如图2,连接,,
四边形是正方形,
,,
,
,
,由(1)知,
,
,
,
,
,
,
,
,
,,
.
23.证明:(1)延长至,使,连接,如图1,
、、、四点共圆,
,
,
,
,
是等边三角形,
,;
又,,
,
、为等边三角形,
,,
在和中,
,
,
;
(2)过点作交于,连接,.如图2,
,
,
,
,
在和中,
,
,
,
;
24.(1).
在和中,.
.
.
;
(2)理由同(1):正方形,正五边形,
(3)正边形.
一、选择题
1.正六边形的边长为,则它的面积为
A. B. C. D.
2.一个圆的内接正六边形与内接正方形的边长之比为
A. B. C. D.
3.如图,正方形内接于,点在上,则的度数为
A. B. C. D.
4.如图,是正六边形的外接圆,点在上不与,重合),则的度数为
A.或 B.或 C. D.
5.在圆内接正六边形中,正六边形的边长为2,则这个正六边形的中心角和边心距分别是
A.,1 B., C., D.,2
6.如图,正方形内接于.点为上一点,连接、,若,,则的长为
A. B. C. D.
7.如图,在一张圆形纸片上剪下一个面积最大的正六边形纸片,它的边长是,的长度是
A. B. C. D.
8.如图,正五边形内接于,点为上一点(点与点,点不重合),连接,,,垂足为,则等于
A. B. C. D.
9.如图,与正六边形的边、分别交于点、,点为劣弧的中点.若,则的半径为
A.2 B. C. D.
10.如图,以正六边形的对角线为边,再作一个正六边形,若,则的长为
A.2 B. C.3 D.
二、填空题
11.两个全等的正方形如图放置,重叠部分为正八边形,且其各边长都为,每个内角均为,则正方形的边长为 .
12.如图,正方形内接于,的半径为6,则的长为 .
13.如图,边长为的正六边形内有两个三角形(数据如图),则 .
14.如图,在正六边形中,于相交于点,则值为 .
15.如图,要拧开一个边长为的正六边形螺料,扳手张开的开口至少为 .
16.如图,正方形和正六边形均内接于,连接;若线段恰好是的一个内接正边形的一条边,则 .
17.如图,正八边形内接于,若,则点到的距离为 .
18.如图,是正五边形的一条对角线,以为圆心,为半径画弧交于点,连接,则 .
三、解答题
19.如图,正方形内接于,,求证:.
20.如图,已知点是正六边形的对称中心,,分别是,上的点,且.
(1)求的度数;
(2)求证:.
21.如图,,,,是上的四个点,.
(1)求证:是等边三角形.
(2)若的半径为2,求等边的边心距.
22.已知,正方形内接于,点是弧上一点.
(1)如图1,若点是弧的中点,求证:;
(2)如图2,若图中,求的值.
23.(1)已知:如图1,是的内接正三角形,点为劣弧上一动点.求证:;
(2)已知:如图2,四边形是的内接正方形,点为劣弧上一动点.求证:.
24.如图1,为等边三角形,图2为正方形,图3为正五边形,图4为正多边形.
(1)如图1当时,请求出的度数,并说明理由
(2)如图2,在正方形中,当时 ;如图3,在正五边形中,当时, ;
(3)如图4,在正边形中,当时,是否有什么规律?如果有请用含有的式子直接表示;如果没有规律,请说明理由.
答案
一、选择题
.. ........
二、填空题
11.. 12.. 13.5. 14.. 15..
16.12. 17.2. 18.72.
三、解答题
19.证明:四边形是正方形,
,
,
,
,即,
.
20.(1)解:六边形是正六边形,
;
(2)证明:连接、,
,
,
,
,
在和中,
,
.
21.(1)证明:在中,
与是对的圆周角,与是所对的圆周角,
,,
又,
,
为等边三角形;
(2)过作于,连接,
则,,
,
,
等边的边心距为1.
22.(1)证明:如图1,连接,
四边形是正方形,
,,
,,
,
点是弧的中点,
,
,
,
,
;
(2)解:如图2,连接,,
四边形是正方形,
,,
,
,
,由(1)知,
,
,
,
,
,
,
,
,
,,
.
23.证明:(1)延长至,使,连接,如图1,
、、、四点共圆,
,
,
,
,
是等边三角形,
,;
又,,
,
、为等边三角形,
,,
在和中,
,
,
;
(2)过点作交于,连接,.如图2,
,
,
,
,
在和中,
,
,
,
;
24.(1).
在和中,.
.
.
;
(2)理由同(1):正方形,正五边形,
(3)正边形.
