九年级数学下册试题 25.2视图-沪科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 25.2视图-沪科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 514.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 00:00:00 | ||
图片预览

文档简介
25.2视图
一、选择题.
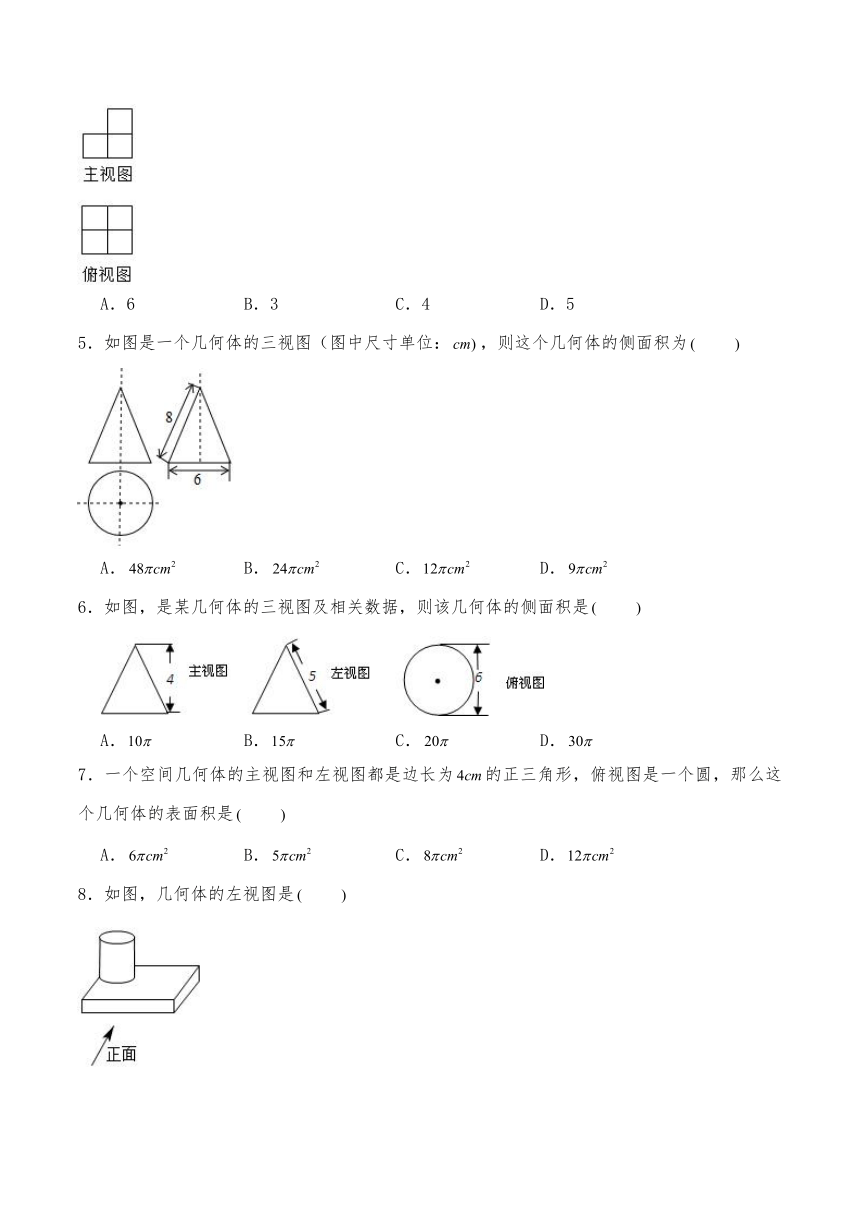
1.一个正方体沿四条棱的中点切割掉一部分后,如图所示,则该几何体的左视图是
A. B. C. D.
2.八个大小相同的正方体搭成的几何体如图所示,其主视图是
A. B. C. D.
3.如图,由七个相同的小正方体拼成立体图形,若从标有①②③④的四个小正方体中取走一个或多个后,余下的几何体与原几何体的左视图相同,则取走的正方体不可能是
A.④ B.③ C.② D.①
4.如图,是由一些大小相同的小正方体搭成的几何体的主视图和俯视图,则搭成该几何体的小正方体的个数最少是
A.6 B.3 C.4 D.5
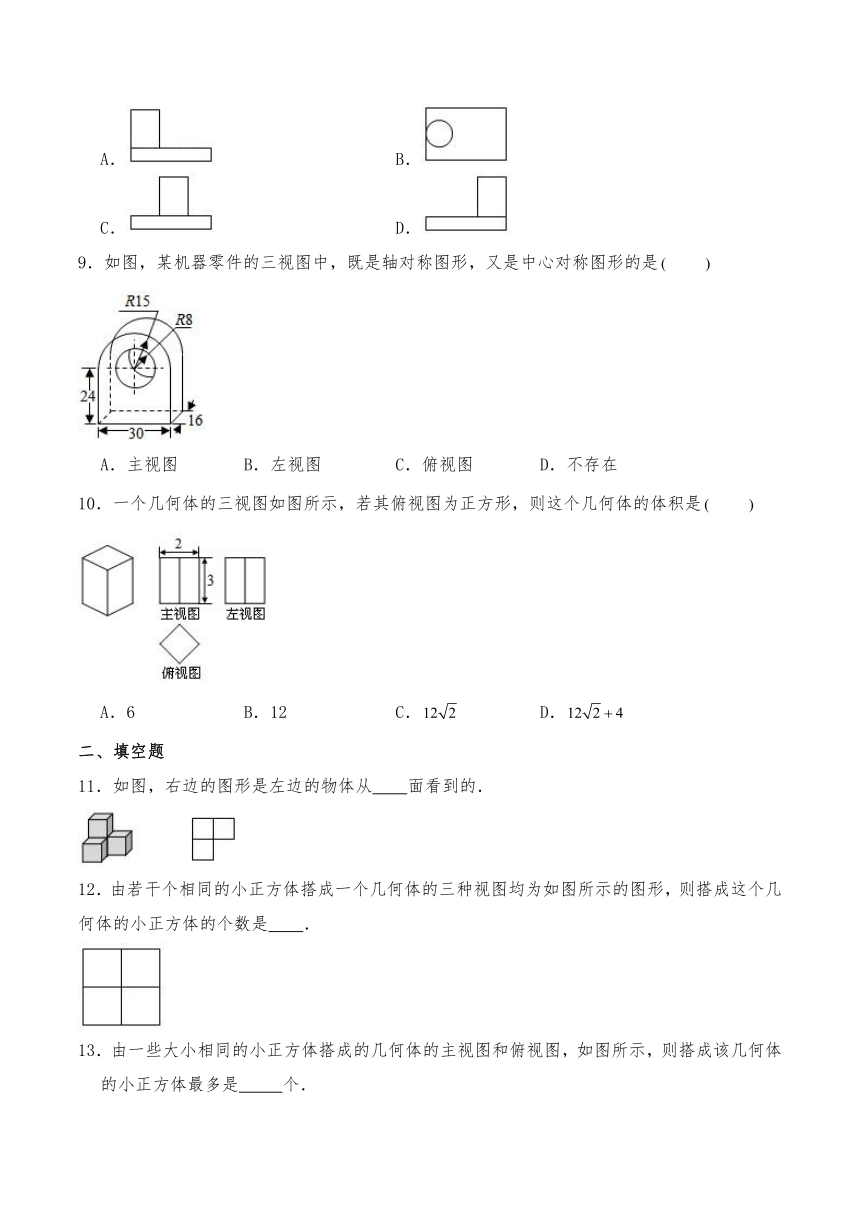
5.如图是一个几何体的三视图(图中尺寸单位:,则这个几何体的侧面积为
A. B. C. D.
6.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是
A. B. C. D.
7.一个空间几何体的主视图和左视图都是边长为的正三角形,俯视图是一个圆,那么这个几何体的表面积是
A. B. C. D.
8.如图,几何体的左视图是
A. B.
C. D.
9.如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是
A.主视图 B.左视图 C.俯视图 D.不存在
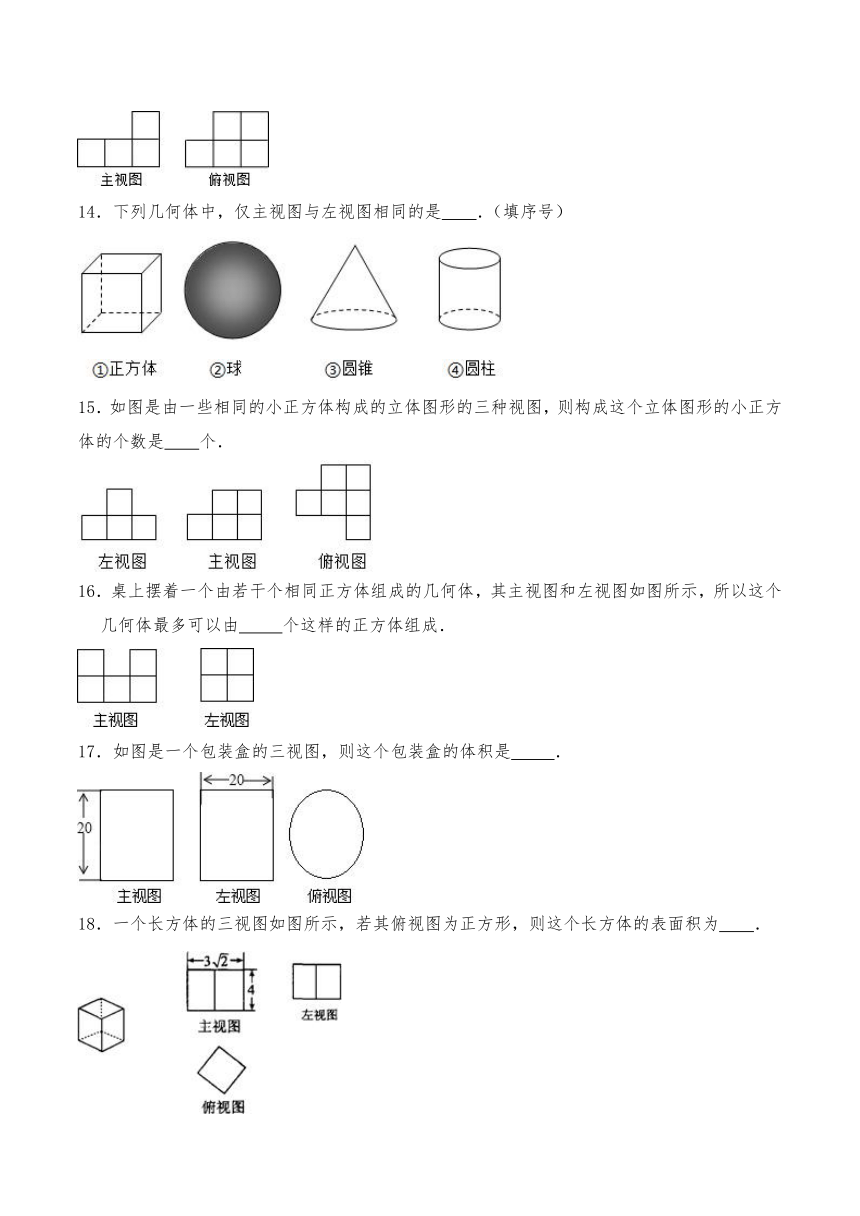
10.一个几何体的三视图如图所示,若其俯视图为正方形,则这个几何体的体积是
A.6 B.12 C. D.
二、填空题
11.如图,右边的图形是左边的物体从 面看到的.
12.由若干个相同的小正方体搭成一个几何体的三种视图均为如图所示的图形,则搭成这个几何体的小正方体的个数是 .
13.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是 个.
14.下列几何体中,仅主视图与左视图相同的是 .(填序号)
15.如图是由一些相同的小正方体构成的立体图形的三种视图,则构成这个立体图形的小正方体的个数是 个.
16.桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,所以这个几何体最多可以由 个这样的正方体组成.
17.如图是一个包装盒的三视图,则这个包装盒的体积是 .
18.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为 .
三、解答题
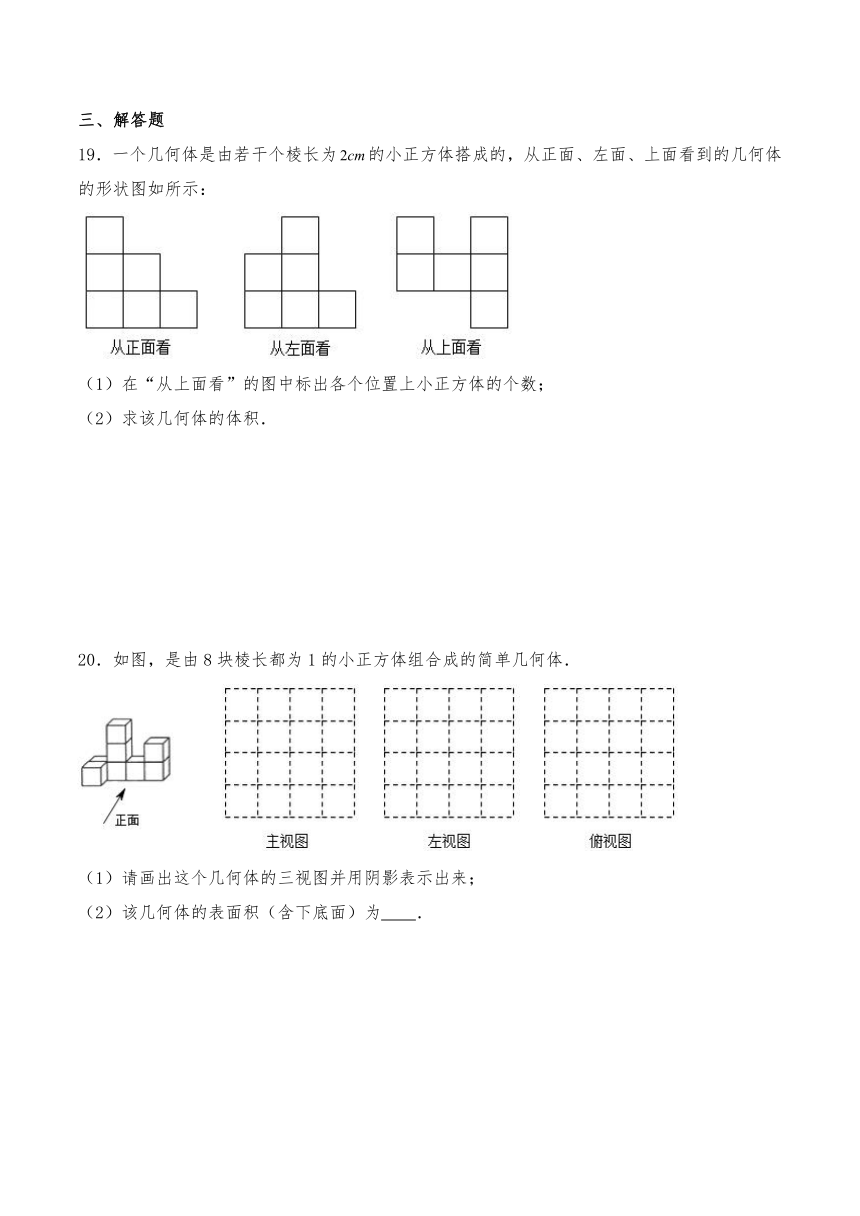
19.一个几何体是由若干个棱长为的小正方体搭成的,从正面、左面、上面看到的几何体的形状图如所示:
(1)在“从上面看”的图中标出各个位置上小正方体的个数;
(2)求该几何体的体积.
20.如图,是由8块棱长都为1的小正方体组合成的简单几何体.
(1)请画出这个几何体的三视图并用阴影表示出来;
(2)该几何体的表面积(含下底面)为 .
21.一个几何体的三种视图如图所示.
(1)这个几何体的名称是 ,其侧面积为 ;
(2)画出它的一种表面展开图;
(3)求出左视图中的长.
22.某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
(1)由三视图可知,密封纸盒的形状是 ;
(2)根据该几何体的三视图,在图2中补全它的表面展开图;
(3)请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)
23.如图,在等腰中,,是的角平分线,且,以点为圆心,长为半径画弧,交于点,交于点.
(1)求由弧及线段、、围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形,将扇形围成一个圆锥的侧面,与正好重合,圆锥侧面无重叠,求这个圆锥的高.
24.如图1,等腰三角形中,,当顶角的大小确定时,它的邻边(即腰或与对边(即底边的比值也就确定,我们把这个比值记作(A),即(A),当时,如.
①理解巩固: , ,(A)的取值范围是 ;
②学以致用:如图2,圆锥的母线长为18,底面直径,一只蚂蚁从点沿着圆锥的侧面爬行到点,求蚂蚁爬行的最短路径长(精确到.
(参考数据:,,
答案
一、选择题
..........
二.填空题
11.上. 12.6或7或8. 13.7.
14.③④. 15.8. 16.10. 17.. 18.66.
三.解答题
19.解:(1)如图所示:
(2)该几何体的体积为:.
答:该几何体的体积为.
20.解:(1)如图所示:
;
(2)该几何体的表面积为:34.
21.解:(1)这个几何体的名称是正三棱柱,
这个几何体的侧面积为.
故答案为:正三棱柱,72;
(2)展开图如下:
(3)在中,作于点,
则,
故左视图中的长为.
22.解:(1)根据该几何体的三视图知道它是一个正六棱柱.
故答案为:正六棱柱;
(2)六棱柱的表面展开图如图(本题只给出一种图形,其它图形请参考给分);
(3)由图中数据可知:六棱柱的高为,底面边长为,
六棱柱的侧面积为.
又密封纸盒的底面面积为:,
六棱柱的表面积为.
23.解:在等腰中,,
,
是的角平分线,
,,
,
,
由弧及线段、、围成图形(图中阴影部分)的面积;
(2)设圆锥的底面圆的半径为,
根据题意得,解得,
这个圆锥的高.
24.解:(1)如图1,,,
则,
,
如图2,,,作于,则,
,
,
;
,
(A)
故答案为:;;(A);
(2)圆锥的底面直径,
圆锥的底面周长为,即侧面展开图扇形的弧长为,
设扇形的圆心角为,
则,
解得,
,
蚂蚁爬行的最短路径长为.
一、选择题.
1.一个正方体沿四条棱的中点切割掉一部分后,如图所示,则该几何体的左视图是
A. B. C. D.
2.八个大小相同的正方体搭成的几何体如图所示,其主视图是
A. B. C. D.
3.如图,由七个相同的小正方体拼成立体图形,若从标有①②③④的四个小正方体中取走一个或多个后,余下的几何体与原几何体的左视图相同,则取走的正方体不可能是
A.④ B.③ C.② D.①
4.如图,是由一些大小相同的小正方体搭成的几何体的主视图和俯视图,则搭成该几何体的小正方体的个数最少是
A.6 B.3 C.4 D.5
5.如图是一个几何体的三视图(图中尺寸单位:,则这个几何体的侧面积为
A. B. C. D.
6.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是
A. B. C. D.
7.一个空间几何体的主视图和左视图都是边长为的正三角形,俯视图是一个圆,那么这个几何体的表面积是
A. B. C. D.
8.如图,几何体的左视图是
A. B.
C. D.
9.如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是
A.主视图 B.左视图 C.俯视图 D.不存在
10.一个几何体的三视图如图所示,若其俯视图为正方形,则这个几何体的体积是
A.6 B.12 C. D.
二、填空题
11.如图,右边的图形是左边的物体从 面看到的.
12.由若干个相同的小正方体搭成一个几何体的三种视图均为如图所示的图形,则搭成这个几何体的小正方体的个数是 .
13.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是 个.
14.下列几何体中,仅主视图与左视图相同的是 .(填序号)
15.如图是由一些相同的小正方体构成的立体图形的三种视图,则构成这个立体图形的小正方体的个数是 个.
16.桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,所以这个几何体最多可以由 个这样的正方体组成.
17.如图是一个包装盒的三视图,则这个包装盒的体积是 .
18.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为 .
三、解答题
19.一个几何体是由若干个棱长为的小正方体搭成的,从正面、左面、上面看到的几何体的形状图如所示:
(1)在“从上面看”的图中标出各个位置上小正方体的个数;
(2)求该几何体的体积.
20.如图,是由8块棱长都为1的小正方体组合成的简单几何体.
(1)请画出这个几何体的三视图并用阴影表示出来;
(2)该几何体的表面积(含下底面)为 .
21.一个几何体的三种视图如图所示.
(1)这个几何体的名称是 ,其侧面积为 ;
(2)画出它的一种表面展开图;
(3)求出左视图中的长.
22.某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
(1)由三视图可知,密封纸盒的形状是 ;
(2)根据该几何体的三视图,在图2中补全它的表面展开图;
(3)请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)
23.如图,在等腰中,,是的角平分线,且,以点为圆心,长为半径画弧,交于点,交于点.
(1)求由弧及线段、、围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形,将扇形围成一个圆锥的侧面,与正好重合,圆锥侧面无重叠,求这个圆锥的高.
24.如图1,等腰三角形中,,当顶角的大小确定时,它的邻边(即腰或与对边(即底边的比值也就确定,我们把这个比值记作(A),即(A),当时,如.
①理解巩固: , ,(A)的取值范围是 ;
②学以致用:如图2,圆锥的母线长为18,底面直径,一只蚂蚁从点沿着圆锥的侧面爬行到点,求蚂蚁爬行的最短路径长(精确到.
(参考数据:,,
答案
一、选择题
..........
二.填空题
11.上. 12.6或7或8. 13.7.
14.③④. 15.8. 16.10. 17.. 18.66.
三.解答题
19.解:(1)如图所示:
(2)该几何体的体积为:.
答:该几何体的体积为.
20.解:(1)如图所示:
;
(2)该几何体的表面积为:34.
21.解:(1)这个几何体的名称是正三棱柱,
这个几何体的侧面积为.
故答案为:正三棱柱,72;
(2)展开图如下:
(3)在中,作于点,
则,
故左视图中的长为.
22.解:(1)根据该几何体的三视图知道它是一个正六棱柱.
故答案为:正六棱柱;
(2)六棱柱的表面展开图如图(本题只给出一种图形,其它图形请参考给分);
(3)由图中数据可知:六棱柱的高为,底面边长为,
六棱柱的侧面积为.
又密封纸盒的底面面积为:,
六棱柱的表面积为.
23.解:在等腰中,,
,
是的角平分线,
,,
,
,
由弧及线段、、围成图形(图中阴影部分)的面积;
(2)设圆锥的底面圆的半径为,
根据题意得,解得,
这个圆锥的高.
24.解:(1)如图1,,,
则,
,
如图2,,,作于,则,
,
,
;
,
(A)
故答案为:;;(A);
(2)圆锥的底面直径,
圆锥的底面周长为,即侧面展开图扇形的弧长为,
设扇形的圆心角为,
则,
解得,
,
蚂蚁爬行的最短路径长为.
