1.3.2 有理数的减法(第一课时) 课件(21张PPT)
文档属性
| 名称 | 1.3.2 有理数的减法(第一课时) 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 10:21:06 | ||
图片预览








文档简介
(共21张PPT)
第1章 有理数
1.3.2 有理数的减法
第一单元
1.理解、掌握有理数的减法法则,会将有理数的减法运算转化为加法运算.(转化思想、几何直观)
2.通过把有理数的减法运算转化为加法运算,渗透转化思想,培养运算能力.(运算能力)
下面是北京冬季某天的气温(-3-3℃).根据你的生活经验,你能说出这天的温差吗?____℃.
6
温差是指最高气温减最低气温.
你还能从温度计上看出3℃比-3℃高多少℃吗?
6
你会列式求这一天北京的温差吗?__________.
3-(-3)
这里用到正数与负数的减法.
减法是加法的逆运算,计算3-(-3),就是求出一个数x,使得x+(-3)=3,因为____+(-3)=3,所以x=_____,即
3-(-3)=____ ①
另一方面,我们知道
3+(+3)=6 ②
由①、②两式,有3-_____=3+_____ ③
6
6
6
(-3)
(+3)
从3-(-3)=3+(+3)能看出减-3相当加哪个数吗?把3换成0,-1,-5,用上面的方法考虑0-(-3),(-1)-(-3),(-5)-(-3).这些数减-3的结果与它们加+3的结果相同吗?
0-(-3)=0+3=3,(-1)-(-3)=(-1)+3=2,(-5)-(-3)=(-5)+3=-2
计算9-8,9+(-8);15-7,15+(-7).从中又能有什么发现吗?
9-8=9+(-8)=1,15-7=15+(-7)=8
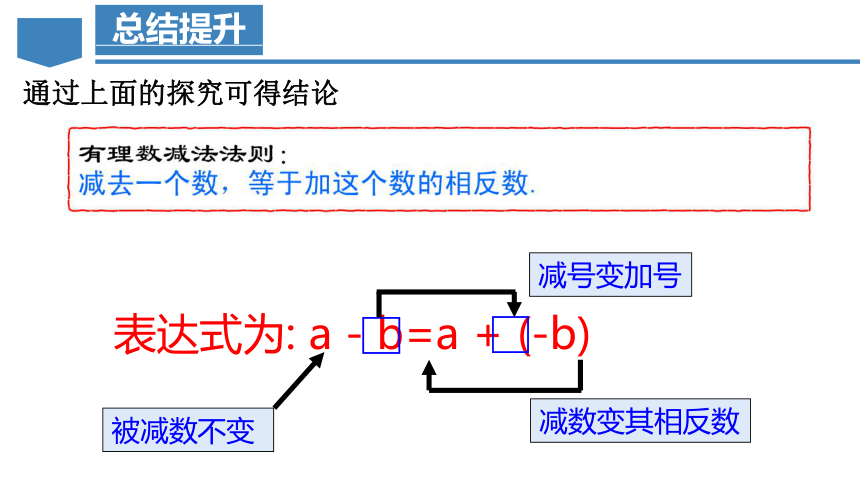
表达式为: a - b=a + (-b)
被减数不变
通过上面的探究可得结论
减号变加号
减数变其相反数
有理数减法法则
重点
例1.计算:
(1)8-15; (2)7-(-5); (3)(-5)-7; (4)(-1.8)-(-3.5);
(5)(-)-(-); (6)0-3; (7)0-(-9).
解:(1)原式=8+(-15)=-7; (2)原式=7+5=12;
(3)原式=(-5)+(-7)=-12; (4)原式=(-1.8)+3.5=1.7;
(5)原式=(-)+=-; (6)原式=0+(-3)=-3; (7)原式=0+9=9.
1.在(-4)-( )=-9中的括号里应填_______.
2.绝对值是的数减去所得的差是__________.
易错点:已知一个数的绝对值,则这个数的取值一般有两种情况,注意不要漏解.
-1
3.计算:
(1)9-13; (2)0-11; (3)0-(-6); (4)4.6-(-3.4);
(5)(-)-; (6)|-3-(-7)|.
解:(1)原式=9+(-13)=-4; (2)原式=0+(-11)=-11;
(3)原式=0+6=6; (4)原式=4.6+3.4=8;
(5)原式=(-)+(-)=-; (6)原式=|-3+7|=4.
在小学,只有当a大于或等于b时,我们才会做a-b(例如2-1,1-1).现在,当a小于b时,你会做a-b(例如1-2,(-1)-1)吗?
一般地,较小的数减较大的数,所得的差是_____数.
负
当a大于或等于b时,a-b≥0;
当a小于b时,a-b<0
有理数的减法运算
重点
例2.计算:
(1)(-)-(-3); (2)(-8)-(-5)-(+1).
解:(1)原式=(-)+3
=2;
(2)原式=(-8)+5+(-1)
=[-8+5+(-1)]+[(-)++(-)]
=(-4)+(-)
=-5.
计算:
(1)(-3)-1; (2)(-2)-(-5)-(+1).
解:(1)原式=(-3)+(-1)
=-5;
(2)原式=(-2)+5+(-1)
=[-8+5+(-1)]+[(-)++(-)]
=2+0
=2.
有理数减法的实际运用
重点
例3.某地一周前四天每天的最高气温与最低气温如表所示,则这四天中温差最大的是( )
A.星期一 B.星期二 C.星期三 D.星期四
C
1.小怡家的冰箱冷藏室温度是5℃,冷冻室温度是-12℃,则她家冰箱冷藏室温度比冷冻室温度高( )
A.13℃ B.-13℃ C.17℃ D.-17℃
2.某市冬季中的一天,中午12时的气温是-3℃,经过6h气温下降了7℃,那么当天18时的气温是______.
3.矿井下A,B,C三处的标高分别是A(-37.5m),B(-129.7m) ,C(-73.2m),最高处比最低处高_______m.
C
-10℃
92.2
数轴在有理数的加减运算中的应用
难点
例4.如图,表示数a,b,c的点在数轴上,且a,b互为相反数.用“>”“<”或“=”号填空:
(1)a+b____0; (2)a+c____0; (3)b+c____0;
(4)a-c____0; (5)b-a____0; (6)c-b____0.
=
<
<
>
<
<
1.已知a,b,c三个数在数轴上对应点的位置如图所示,下列各式错误的是( )
A.b0
2.有理数a,b,c,d在数轴上的对应点的位置如图所示,则下列运算结果中是正确的有( )
①a-b; ②b-c; ③d-a; ④c-a.
A.1个 B.2个 C.3个 D.4个
B
B
利用作差法比较两个有理数的大小
难点
例5.阅读材料:
比较-和-的大小.
解:(-)-(-)=-+=-+=>0,则->-.
试用这种方法比较和-和-的大小.
解:--(-)=-+=-+=-<0,则-<-
比较大小:
(1)- ____ -; (2)- ____ -; (3)- ____ -
解:(1)--(-)=-+=-+=0,则->-
(2)--(-)=-+=-+=-0,则-<-
(3)--(-)=-+=-+=0,则->-
>
<
>
利用有理数的减法求数轴上两点之间的距离
难点
例6.根据图中数轴提供的信息,回答下列问题:
(1)A,B两点之间的距离是多少 (2)B,C两点之间的距离是多少
解:点A表示的数是2,点B表示的数是-,点C表示的数是-3.
(1)A,B两点之间的距离是==;
(2)B,C两点之间的距离是==.
1.数轴上表示-8的点与表示2的点之间的距离为______.
2.数轴上表示-3.7的点与表示-1.9的点之间的距离为_______.
3.如图,数轴上M,N两点所对应的数分别为m,n,则m-n的结果可能是( )
A.-1 B.1 C.2 D.3
10
C
1.8
有理数的减法法则是一个转化法则,减号转化为加号,同时要注意减数变为它的相反数,这样就可以用加法来解决减法问题.
第1章 有理数
1.3.2 有理数的减法
第一单元
1.理解、掌握有理数的减法法则,会将有理数的减法运算转化为加法运算.(转化思想、几何直观)
2.通过把有理数的减法运算转化为加法运算,渗透转化思想,培养运算能力.(运算能力)
下面是北京冬季某天的气温(-3-3℃).根据你的生活经验,你能说出这天的温差吗?____℃.
6
温差是指最高气温减最低气温.
你还能从温度计上看出3℃比-3℃高多少℃吗?
6
你会列式求这一天北京的温差吗?__________.
3-(-3)
这里用到正数与负数的减法.
减法是加法的逆运算,计算3-(-3),就是求出一个数x,使得x+(-3)=3,因为____+(-3)=3,所以x=_____,即
3-(-3)=____ ①
另一方面,我们知道
3+(+3)=6 ②
由①、②两式,有3-_____=3+_____ ③
6
6
6
(-3)
(+3)
从3-(-3)=3+(+3)能看出减-3相当加哪个数吗?把3换成0,-1,-5,用上面的方法考虑0-(-3),(-1)-(-3),(-5)-(-3).这些数减-3的结果与它们加+3的结果相同吗?
0-(-3)=0+3=3,(-1)-(-3)=(-1)+3=2,(-5)-(-3)=(-5)+3=-2
计算9-8,9+(-8);15-7,15+(-7).从中又能有什么发现吗?
9-8=9+(-8)=1,15-7=15+(-7)=8
表达式为: a - b=a + (-b)
被减数不变
通过上面的探究可得结论
减号变加号
减数变其相反数
有理数减法法则
重点
例1.计算:
(1)8-15; (2)7-(-5); (3)(-5)-7; (4)(-1.8)-(-3.5);
(5)(-)-(-); (6)0-3; (7)0-(-9).
解:(1)原式=8+(-15)=-7; (2)原式=7+5=12;
(3)原式=(-5)+(-7)=-12; (4)原式=(-1.8)+3.5=1.7;
(5)原式=(-)+=-; (6)原式=0+(-3)=-3; (7)原式=0+9=9.
1.在(-4)-( )=-9中的括号里应填_______.
2.绝对值是的数减去所得的差是__________.
易错点:已知一个数的绝对值,则这个数的取值一般有两种情况,注意不要漏解.
-1
3.计算:
(1)9-13; (2)0-11; (3)0-(-6); (4)4.6-(-3.4);
(5)(-)-; (6)|-3-(-7)|.
解:(1)原式=9+(-13)=-4; (2)原式=0+(-11)=-11;
(3)原式=0+6=6; (4)原式=4.6+3.4=8;
(5)原式=(-)+(-)=-; (6)原式=|-3+7|=4.
在小学,只有当a大于或等于b时,我们才会做a-b(例如2-1,1-1).现在,当a小于b时,你会做a-b(例如1-2,(-1)-1)吗?
一般地,较小的数减较大的数,所得的差是_____数.
负
当a大于或等于b时,a-b≥0;
当a小于b时,a-b<0
有理数的减法运算
重点
例2.计算:
(1)(-)-(-3); (2)(-8)-(-5)-(+1).
解:(1)原式=(-)+3
=2;
(2)原式=(-8)+5+(-1)
=[-8+5+(-1)]+[(-)++(-)]
=(-4)+(-)
=-5.
计算:
(1)(-3)-1; (2)(-2)-(-5)-(+1).
解:(1)原式=(-3)+(-1)
=-5;
(2)原式=(-2)+5+(-1)
=[-8+5+(-1)]+[(-)++(-)]
=2+0
=2.
有理数减法的实际运用
重点
例3.某地一周前四天每天的最高气温与最低气温如表所示,则这四天中温差最大的是( )
A.星期一 B.星期二 C.星期三 D.星期四
C
1.小怡家的冰箱冷藏室温度是5℃,冷冻室温度是-12℃,则她家冰箱冷藏室温度比冷冻室温度高( )
A.13℃ B.-13℃ C.17℃ D.-17℃
2.某市冬季中的一天,中午12时的气温是-3℃,经过6h气温下降了7℃,那么当天18时的气温是______.
3.矿井下A,B,C三处的标高分别是A(-37.5m),B(-129.7m) ,C(-73.2m),最高处比最低处高_______m.
C
-10℃
92.2
数轴在有理数的加减运算中的应用
难点
例4.如图,表示数a,b,c的点在数轴上,且a,b互为相反数.用“>”“<”或“=”号填空:
(1)a+b____0; (2)a+c____0; (3)b+c____0;
(4)a-c____0; (5)b-a____0; (6)c-b____0.
=
<
<
>
<
<
1.已知a,b,c三个数在数轴上对应点的位置如图所示,下列各式错误的是( )
A.b
2.有理数a,b,c,d在数轴上的对应点的位置如图所示,则下列运算结果中是正确的有( )
①a-b; ②b-c; ③d-a; ④c-a.
A.1个 B.2个 C.3个 D.4个
B
B
利用作差法比较两个有理数的大小
难点
例5.阅读材料:
比较-和-的大小.
解:(-)-(-)=-+=-+=>0,则->-.
试用这种方法比较和-和-的大小.
解:--(-)=-+=-+=-<0,则-<-
比较大小:
(1)- ____ -; (2)- ____ -; (3)- ____ -
解:(1)--(-)=-+=-+=0,则->-
(2)--(-)=-+=-+=-0,则-<-
(3)--(-)=-+=-+=0,则->-
>
<
>
利用有理数的减法求数轴上两点之间的距离
难点
例6.根据图中数轴提供的信息,回答下列问题:
(1)A,B两点之间的距离是多少 (2)B,C两点之间的距离是多少
解:点A表示的数是2,点B表示的数是-,点C表示的数是-3.
(1)A,B两点之间的距离是==;
(2)B,C两点之间的距离是==.
1.数轴上表示-8的点与表示2的点之间的距离为______.
2.数轴上表示-3.7的点与表示-1.9的点之间的距离为_______.
3.如图,数轴上M,N两点所对应的数分别为m,n,则m-n的结果可能是( )
A.-1 B.1 C.2 D.3
10
C
1.8
有理数的减法法则是一个转化法则,减号转化为加号,同时要注意减数变为它的相反数,这样就可以用加法来解决减法问题.
