直线与圆相切的复习课[上学期]
图片预览

文档简介
(共8张PPT)
千秋外国语学校沈朝杰
O
.
A
B
60°
C
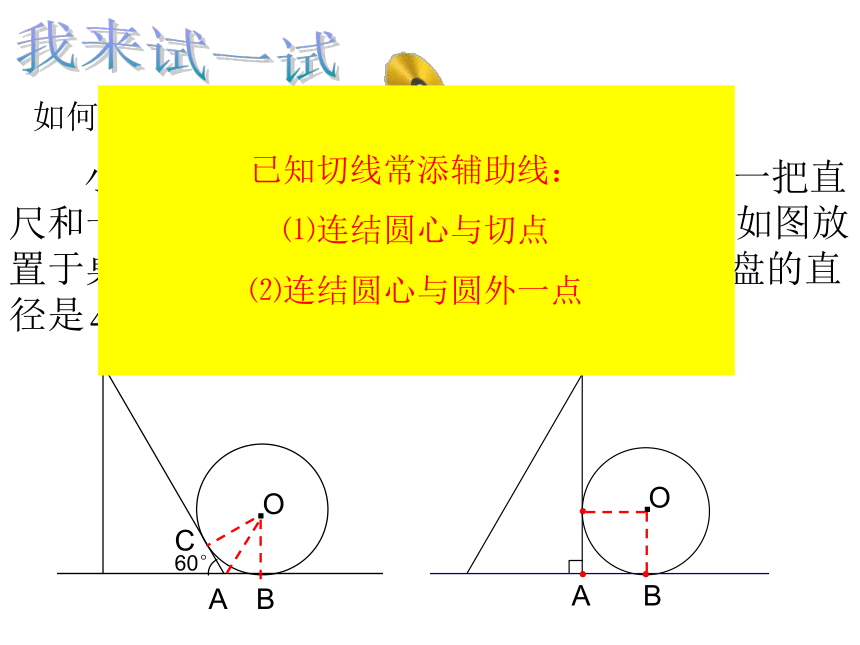
小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=2cm,他就知道光盘的直径是 cm,你知道为什么吗?
如何测量光盘的直径
已知切线常添辅助线:
⑴连结圆心与切点
⑵连结圆心与圆外一点
O
.
A
C
60°
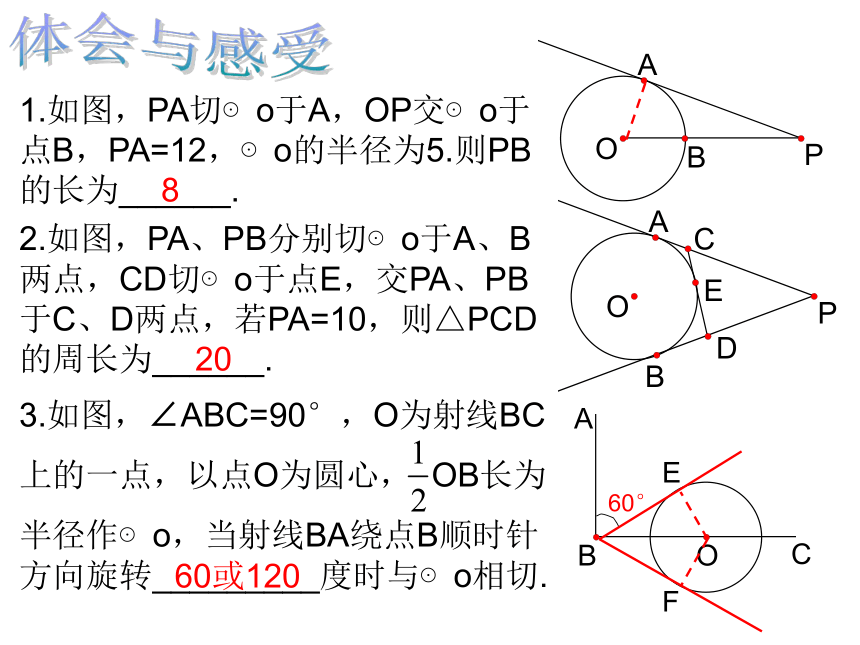
1.如图,PA切⊙o于A,OP交⊙o于点B,PA=12,⊙o的半径为5.则PB的长为______.
2.如图,PA、PB分别切⊙o于A、B两点,CD切⊙o于点E,交PA、PB于C、D两点,若PA=10,则△PCD的周长为______.
3.如图,∠ABC=90°,O为射线BC
上的一点,以点O为圆心, OB长为
半径作⊙o,当射线BA绕点B顺时针方向旋转_________度时与⊙o相切.
8
20
60或120
E
F
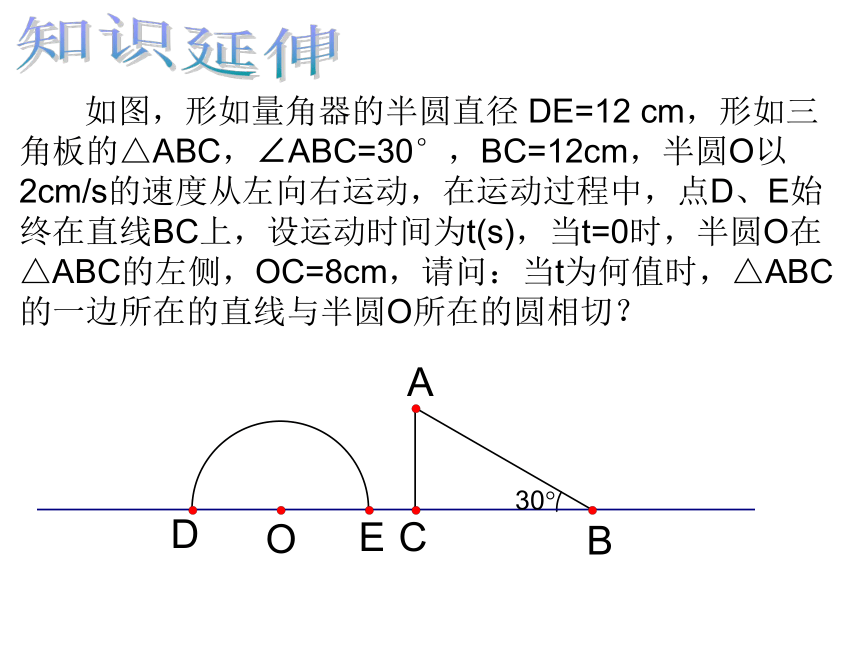
如图,形如量角器的半圆直径 DE=12 cm,形如三角板的△ABC,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0时,半圆O在△ABC的左侧,OC=8cm,请问:当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
D
O
C(E)
E
B
A
D
O
C(D)
E
B(E)
A
解:(1)⊙o与AC 相切
① ⊙o在AC左侧
此时⊙o运动的路程EC=OC-OE=8-6=2,所以t=1.
② ⊙o在AC右侧
因为DE=BC,所以⊙o运动的路程为EB.因为EB=EC+BC=2+12=14,所以t=7.
D
O
C(O)
E
B
A
E
F
(2)⊙o与AB 相切
① ⊙o在AB左侧
连结OF,则OF⊥AB
∵∠ABC=30°
此时⊙o运动的路程为OC=8,所以t=4.
∴OB=2OF=12
即点O和点C重合,
D
O
C
E
B
A
E
O’
G
② ⊙o在AB右侧
∴O’B=2O’G=12
连结O’G,则O’G⊥AG
∵∠O’BG=∠ABC=30°
此时⊙o运动的路程为OO’=OC+BC+O’B=32,所以t=16.
综上所述,当t=2、4、7、16秒时, △ABC的一边所在的直线与半圆O所在的圆相切.
谈谈你的收获……
1.切线的性质;切线长定理.
2.已知切线常添辅助线:
⑴连结圆心与切点
⑵连结圆心与圆外一点
3.常用的数学思想方法:转化;分类讨论等等.
千秋外国语学校沈朝杰
O
.
A
B
60°
C
小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=2cm,他就知道光盘的直径是 cm,你知道为什么吗?
如何测量光盘的直径
已知切线常添辅助线:
⑴连结圆心与切点
⑵连结圆心与圆外一点
O
.
A
C
60°
1.如图,PA切⊙o于A,OP交⊙o于点B,PA=12,⊙o的半径为5.则PB的长为______.
2.如图,PA、PB分别切⊙o于A、B两点,CD切⊙o于点E,交PA、PB于C、D两点,若PA=10,则△PCD的周长为______.
3.如图,∠ABC=90°,O为射线BC
上的一点,以点O为圆心, OB长为
半径作⊙o,当射线BA绕点B顺时针方向旋转_________度时与⊙o相切.
8
20
60或120
E
F
如图,形如量角器的半圆直径 DE=12 cm,形如三角板的△ABC,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0时,半圆O在△ABC的左侧,OC=8cm,请问:当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
D
O
C(E)
E
B
A
D
O
C(D)
E
B(E)
A
解:(1)⊙o与AC 相切
① ⊙o在AC左侧
此时⊙o运动的路程EC=OC-OE=8-6=2,所以t=1.
② ⊙o在AC右侧
因为DE=BC,所以⊙o运动的路程为EB.因为EB=EC+BC=2+12=14,所以t=7.
D
O
C(O)
E
B
A
E
F
(2)⊙o与AB 相切
① ⊙o在AB左侧
连结OF,则OF⊥AB
∵∠ABC=30°
此时⊙o运动的路程为OC=8,所以t=4.
∴OB=2OF=12
即点O和点C重合,
D
O
C
E
B
A
E
O’
G
② ⊙o在AB右侧
∴O’B=2O’G=12
连结O’G,则O’G⊥AG
∵∠O’BG=∠ABC=30°
此时⊙o运动的路程为OO’=OC+BC+O’B=32,所以t=16.
综上所述,当t=2、4、7、16秒时, △ABC的一边所在的直线与半圆O所在的圆相切.
谈谈你的收获……
1.切线的性质;切线长定理.
2.已知切线常添辅助线:
⑴连结圆心与切点
⑵连结圆心与圆外一点
3.常用的数学思想方法:转化;分类讨论等等.
