2022-2023学年河北省石家庄市裕华区七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年河北省石家庄市裕华区七年级(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 404.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 13:21:26 | ||
图片预览




文档简介
2022-2023学年河北省石家庄市裕华区七年级(下)期末数学试卷
一、选择题(本大题共16小题,共32.0分。在每小题列出的选项中,选出符合题目的一项)
1. 可燃冰是一种新型能源,它的密度很小,可燃冰的质量仅为数字用科学记数法表示是( )
A. B. C. D.
2. 已知,下列式子不成立的是( )
A. B. C. D.
3. 如图,某地进行城市规划,在一条新修公路旁有一村庄,现要建一个汽车站,且有,,,四个地点可供选择若要使汽车站离村庄最近,则选择在点处建汽车站的依据是( )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 点到直线的距离 D. 垂线段最短
4. 下列变形中是因式分解的是( )
A. B.
C. D.
5. 山上的一段观光索道如图所示,索道支撑架均为互相平行,且每两个支撑架之间的索道均是直的,若,,则( )
A. B. C. D.
6. 运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了次后就停止,则最小整数值取多少( )
A. B. C. D.
7. 如图,直线,点是直线上一个动点,当点的位置发生变化时,的面积( )
A. 向左移动变小
B. 向右移动变小
C. 始终不变
D. 无法确定
8. 下列命题中的假命题是( )
A. 当时,有
B. 经过已知直线外一点,有且只有一条直线与已知直线平行
C. 互为相反数的两个数的和为
D. 相等的角是对顶角
9. 若、为正整数,则( )
A. B. C. D.
10. 将一副三角尺如图放置,其中,,,则的度数为( )
A.
B.
C.
D.
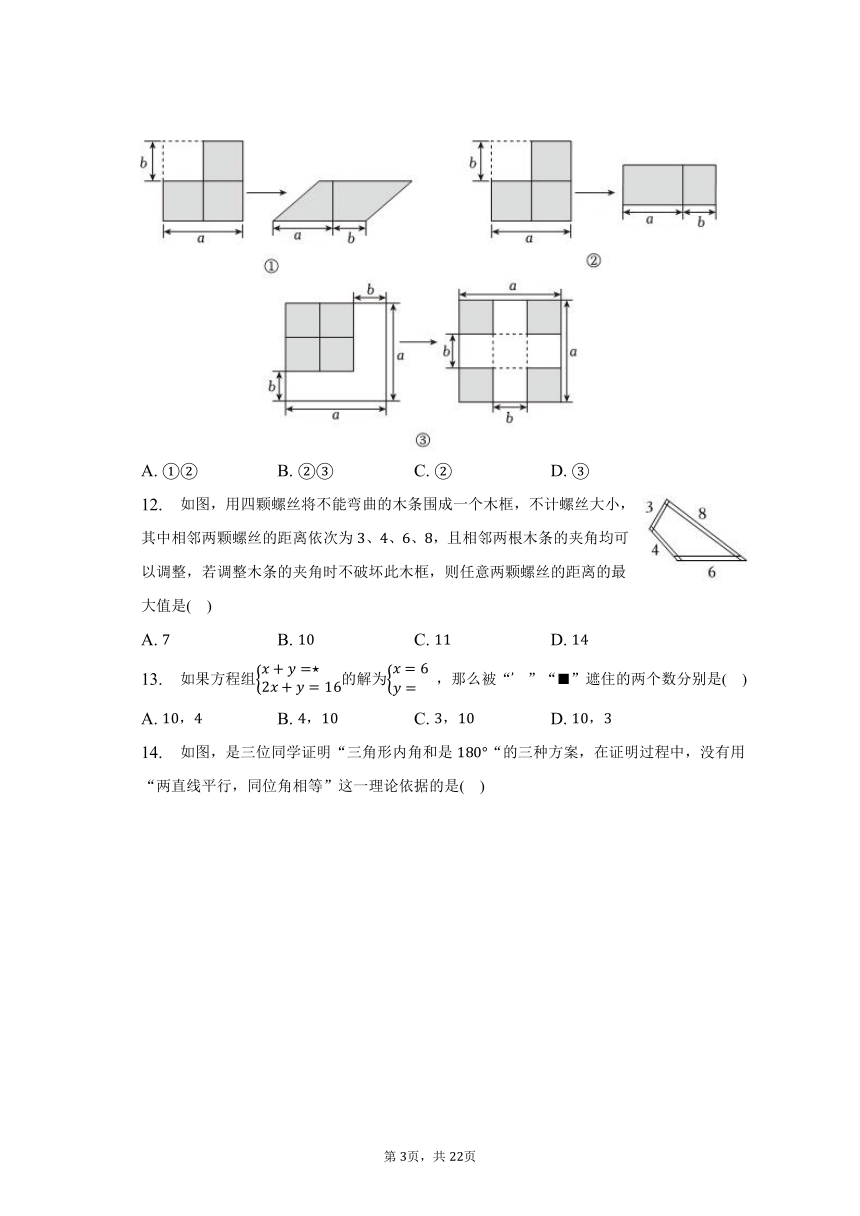
11. 下面给出的三幅图都是将阴影部分通过割,拼,形成新的图形,其中不能验证平方差公式的是( )
A. B. C. D.
12. 如图,用四颗螺丝将不能弯曲的木条围成一个木框,不计螺丝大小,其中相邻两颗螺丝的距离依次为、、、,且相邻两根木条的夹角均可以调整,若调整木条的夹角时不破坏此木框,则任意两颗螺丝的距离的最大值是( )
A. B. C. D.
13. 如果方程组的解为,那么被“”“”遮住的两个数分别是( )
A. , B. , C. , D. ,
14. 如图,是三位同学证明“三角形内角和是“的三种方案,在证明过程中,没有用“两直线平行,同位角相等”这一理论依据的是( )
方案Ⅰ 方案Ⅱ 方案Ⅲ
过点作,
则,
,
. 过点作,
则,,
. 过点作,
则,,
,
.
A. 方案Ⅰ和方案Ⅱ B. 方案Ⅱ和方案Ⅲ C. 方案Ⅰ和方案Ⅲ D. 都没用到
15. 不等式组的整数解的个数是( )
A. B. C. D.
16. 三角形中,如果一个角是另一个角的倍,这样的三角形我们称之为“灵动三角形”例如,三个内角分别为、、的三角形是“灵动三角形”如图,,
在射线上找一点,过点作交于点,以为端点作射线,交线段于点我们规定.
的度数为;
是“灵动三角形”;
若,则是“灵动三角形”;
当为“灵动三角形”时,为或
结论正确的有个.( )
A. B. C. D.
二、填空题(本大题共3小题,共7.0分)
17. 如图,中,、分别是,的中点,的面积是,则阴影部分的面积是______ .
18. 多项式是一个完全平方式,则______.
19. 要度量作业纸上两条相交直线、所夹锐角的大小,发现其交点不在作业纸内,无法直接度量.
小明的方案:画直线与、相交,如图,测得,,则 ______ 用含、的代数式表示;
小刚的方案:画直线与、相交,再画、相邻的外角的角平分线交于点,如图,则得,则 ______ 用含的代数式表示.
三、解答题(本大题共7小题,共61.0分。解答应写出文字说明,证明过程或演算步骤)
20. 本小题分
计算:;
;
;
因式分解:.
解不等式组,并把它的解集在数轴上表示出来.
解方程组:.
21. 本小题分
在边长为的方格纸中有一个.
作出的高,并求出面积.
将向上平移个单位,再向左平移个单位,得到,请画出.
请任意写出一组平移前后两个三角形中平行且相等的线段.
22. 本小题分
杨老师在黑板上布置了一道题,小白和小红展开了下面的讨论:
已知时,求代数式:的值.
这道题与无关,是可以解的.
只知道的值,没有告诉的值,求不出答案.
根据上述情景,你认为谁说得对?为什么?并求出代数式的值.
23. 本小题分
如图,,,,请将求的过程填写完整.
解:因为
所以____________
又因为
所以______
所以____________
所以____________
因为
所以______
24. 本小题分
发现:任意两个连续奇数的平方差是的倍数.
验证:如,,请求出它的结果是的几倍?
探究:设两个连续奇数为,其中为正整数,请论证“发现”中的结论正确;
延伸:两个连续偶数的平方差是______ 的倍数.
25. 本小题分
某商场计划经销、两种新型节能台灯共盏,这两种台灯的进价、售价如表所示:
型 型
进价元盏
售价元盏
若该商场购进这批台灯共用去元,问这两种台灯各购进多少盏?
在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于元,问至少购进种台灯多少盏?
26. 本小题分
如图,把一块含的直角三角板的边放置于长方形直尺的边上.
如图,现把三角板绕点逆时针旋转,当,且点恰好落在边上时,请直接写出 ______ , ______ 结果用含的代数式表示;
在的条件下,若恰好是的倍,求的值.
如图三角板的放置,现将射线绕点以每秒的转速逆时针旋转得到射线,同时射线绕点以每秒的转速顺时针旋转得到射线,当射线旋转至与重合时,则射线、均停止转动,设旋转时间为在旋转过程中,是否存在,若存在,求出此时的值;若不存在,请说明理由.
答案和解析
1.【答案】
【解析】解:.
故选:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
2.【答案】
【解析】解:,
,
故选项A不符合题意;
,
,
故选项B不符合题意;
,
,
故选项C不符合题意;
,,
,
故选项D符合题意.
故选:.
根据不等式的性质,逐项判断即可.
此题主要考查了不等式的性质:不等式的两边同时乘或除以同一个正数,不等号的方向不变;不等式的两边同时乘或除以同一个负数,不等号的方向改变;不等式的两边同时加上或减去同一个数或同一个含有字母的式子,不等号的方向不变.
3.【答案】
【解析】解:根据题意得:要使汽车站离村庄最近,则选择在点处建汽车站的依据是垂线段最短.
故选:.
根据垂线段最短,即可求解.
本题考查了垂线段最短,熟练掌握垂线段最短的知识点是解此题的关键.
4.【答案】
【解析】解:由因式分解的定义可得,
选项等式右边不是积的形式不是因式分解,不符合题意;
选项是因式分解,符合题意;
选项等式右边不是积的形式不是因式分解,不符合题意;
选项等式右边不是积的形式不是因式分解,不符合题意;
故选:.
根据因式分解的定义:将一个多项式写成几个整式的积的形式,直接判断即可得到答案.
本题考查因式分解的定义:将一个多项式写成几个整式的积的形式叫因式分解.
5.【答案】
【解析】解:如图所示,过点作,
,
,
,,
,
故选:.
如图所示,过点作,则,由平行线的性质进行求解即可.
本题主要考查了平行线的性质,熟知两直线平行,内错角相等是解题的关键.
6.【答案】
【解析】解:依题意,得:,
解得:.
为整数,
的最小值为.
故选:.
根据程序操作进行了次后就停止,即可得出关于的一元一次不等式,解之即可得出的取值范围,再取其中最小的整数值即可得出结论.
本题考查了一元一次不等式的应用,找准等量关系,正确列出一元一次不等式是解题的关键.
7.【答案】
【解析】解:直线,点是直线上一个动点,
无论点怎么移动,点到的距离不变,
的底不变,高不变,面积也不变,
故选:.
根据平行线间的距离处处相等可得点到的距离不变,因此三角形的面积不变.
本题考查平行线间的距离,掌握平行线间的距离处处相等是解题的关键.
8.【答案】
【解析】解:、当时,有,所以为真命题;
B、经过已知直线外一点,有且只有一条直线与已知直线平行,所以为真命题;
C、互为相反数的两个数的和为,所以为真命题;
D、相等的角不一定是对顶角,所以为假命题.
故选D.
根据乘方的意义对进行判断;根据经过已知直线外一点,有且只有一条直线与已知直线平行对进行判断;根据相反数的定义对进行判断;根据对顶角的定义对进行判断.
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果那么”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.
9.【答案】
【解析】解:由题意,原式.
故选:.
依据题意,由乘方的意义及同底数幂的乘法进行计算可以得解.
本题考查了乘方的意义及同底数幂的乘法,需要熟练掌握并理解.
10.【答案】
【解析】解:,
,
,
.
又,
.
故选:.
由,利用“同位角相等,两直线平行”,可得出,利用“两直线平行,同位角相等”,可求出的度数,结合,可求出的度数,再利用邻补角互补,即可求出的度数.
本题考查了平行线的判定与性质以及邻补角,根据各角之间的关系,求出的度数是解题的关键.
11.【答案】
【解析】解:图中,将阴影部分沿着虚线裁剪,可以拼成右侧的平行四边形,
阴影部分面积可以看作两个正方形的面积差,即,所拼成的是底为,高为的平行四边形,因此面积为,所以有,
所以图可以验证平方差公式,不符合题意;
图中阴影部分面积可以看作两个正方形的面积差,即,所拼成的长方形的长为,款为,因此面积为,所以有,
因此图可以验证平方差公式,不符合题意;
图中阴影部分可以看作是边长为的正方形,因此面积为,所拼成的图形中阴影部分的面积可以看作四个小正方形的面积和,,因此不能验证平方差公式,符合题意;
故选:.
根据各个图形中阴影部分面积的“算两次”,进而判断是否验证平方差公式即可.
本题考查平方差公式,掌握平方差公式的结构特征是正确解答的前提,用代数式表示图形中阴影部分的面积是解决问题的关键.
12.【答案】
【解析】解:其中相邻两颗螺丝的距离依次为、、、,
任意两颗螺丝的距离的最大值是,
故选:.
根据三角形的三边关系即可得到结论.
本题考查了三角形的三边关系,熟练掌握三角形的三边关系是解题的关键.
13.【答案】
【解析】解:把代入得,解得,
再把代入得,
故选:.
把代入先求出,再代入求.
本题主要考查了二元一次方程组的解,解题的关键是理解题意,代入法求解.
14.【答案】
【解析】解:方案Ⅰ,过点作,
则两直线平行内错角相等,两直线平行同旁内角互补,
;
方案Ⅱ,过点作,
则两直线平行内错角相等,两直线平行同位角相等,
,
;
方案Ⅲ,过点作,
则两直线平行内错角相等,两直线平行内错角相等,
,
.
方案Ⅰ和方案Ⅲ都没用到“两直线平行,同位角相等”这一理论依据,而方案Ⅱ用到了.
故选:.
根据平行线的性质即可求解.
本题考查了平行线的性质,掌握两直线平行,同位角相等;两直线平行内错角相等;两直线平行同旁内角互补是解题的关键.
15.【答案】
【解析】解:,
解不等式得,
解不等式得.
则不等式组的解集是:.
则整数解是、、,共有个.
故选:.
首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,根据不等式组的解集确定整数解及其个数即可.
此题考查的是一元一次不等式组的解法和一元一次不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
16.【答案】
【解析】解:,
,
,
,
,
是“灵动三角形”,故正确,
,,
,
,
是“灵动三角形”故正确,
是“灵动三角形”,
时,,;
当时,,.
当时,,可得.
综上所述,满足条件的值为或或故错误,
综上所述,正确的有:,共个.
故选:.
根据直角三角形两锐角互余求解.
根据“灵动三角形”的定义判断即可.
根据“灵动三角形”的定义判断即可.
分三种情形,利用三角形内角和定理求解即可.
本题考查三角形内角和定理,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
17.【答案】
【解析】解:是的中点,的面积是,
,
是的中点,
,
故答案为:.
根据三角形中线平分三角形面积进行求解即可.
本题主要考查了三角形中线的性质,熟知三角形中线平分三角形面积是解题的关键.
18.【答案】
【解析】解:是一个完全平方式,
,
故答案为.
根据完全平方公式的灵活应用,这里中间项为减去和的乘积的倍,那么末项是的平方.
本题主要考查完全平方公式,根据两平方项确定出这两个数,再根据乘积二倍项求解.
19.【答案】
【解析】解:,和正好是一个三角形的三个内角,
,
.
故答案为:.
,分别是、的平分线,
,,
,,
即:,,
,,
,
,
,
,
由可知:
故答案为:.
根据,和正好是一个三角形的三个内角,然后根据三角形的内角和定理即可得出答案;
首先根据角平分线的定义得,,再根据邻补角的定义得,,据此得,再根据三角形的内角和定理得可得出,据此可得,然后再利用的结论可得出答案.
此题主要考查了三角形的内角和定理,邻补角的定义,角平分线的定义等,解答此题的关键是熟练掌握三角形的内角和等于.
20.【答案】解:原式
;
原式
;
原式
;
原式
;
,
由得:,
由得:,
不等式组的解集为,
数轴表示如下:
;
,
得:,
解得:,
把代入得:,
解得:,
则方程组的解为.
【解析】原式利用乘方的意义,零指数幂、负整数指数幂法则计算即可求出值;
原式利用幂的乘方运算法则,以及同底数幂的乘除法则计算即可求出值;
原式利用多项式乘多项式,以及单项式乘多项式法则计算,去括号合并即可得到结果;
原式提取公因式,再利用完全平方公式分解即可;
分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,表示在数轴上即可;
方程组利用加减消元法求出解即可.
此题考查了整式的混合运算,提公因式法与公式法的综合运用,解二元一次方程组,实数的运算,以及解一元一次不等式组,熟练掌握各自的解法及运算法则是解本题的关键.
21.【答案】解:高如图所示,.
先将点,,分别向上平移个单位,再向左平移个单位确定点,,,再连接,,,此时即为所求.
与相等且平行,与相等且平行,与相等且平行,三组线段任写一组.
【解析】根据三角形的高的定义画出图形即可.
先将点,,分别向上平移个单位,再向左平移个单位确定点,,,再连接,,,此时即为所求.
利用平移的性质判断即可.
本题考查作图平移变换,平行线的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
22.【答案】解:小红说得对.
理由:
.
化简结果中不含,所以值与取值无关.
所以小红说得对.
当时,
原式.
【解析】利用乘法法则化简给出的代数式,根据化简结果判断谁说得对并求值即可.
本题主要考查了整式的化简求值,掌握整式的乘法公式是解决本题的关键.
23.【答案】 两直线平行,同位角相等 等量代换 内错角相等,两直线平行 两直线平行,同旁内角互补
【解析】解:,
两直线平行,同位角相等,
,
等量代换,
内错角相等,两直线平行,
两直线平行,同旁内角互补,
,
,
故答案为:;两直线平行,同位角相等;等量代换;;内错角相等,两直线平行;;两直线平行,同旁内角互补;.
根据平行线的性质推出,推出,根据平行线的性质得出,代入求出即可.
本题主要考查了平行线的判定与性质,理解平行线的判定与性质进行证明是解此题的关键.
24.【答案】
【解析】解:验证:,
是的倍.
探究:,
两个连续奇数,的平方差是的倍数.
延伸:两个连续偶数的平方差是的倍数.
理由如下:
设两个连续的偶数分别为:,,
,
两个连续偶数的平方差是的倍数.
故答案为:.
验证通过计算即可得出答案;
探究应用因式分解的方法计算,据此可得出结论;
延伸:首先设两个连续的偶数分别为:,,再计算,据此可得出答案.
此题主要考查了因式分解的应用,解答此题的关键是在有理数的运算和整式的运算中熟练应用完全平方公式和平方差公式.
25.【答案】解:设购进种新型节能台灯盏,购进种新型节能台灯盏,
依题意,得:,
解得:.
答:购进种新型节能台灯盏,购进种新型节能台灯盏.
设购进种新型节能台灯盏,则购进种新型节能台灯盏,
依题意,得:,
解得:.
为正整数,
的最小值为.
答:至少购进种台灯盏.
【解析】设购进种新型节能台灯盏,购进种新型节能台灯盏,根据总价单价数量结合该商城用元购进、两种新型节能台灯共盏,即可得出关于,的二元一次方程组,解之即可得出结论;
设购进种新型节能台灯盏,则购进种新型节能台灯盏,根据总利润单盏利润数量结合总利润不少于元,即可得出关于的一元一次不等式,解之取其中的最小整数值即可得出结论.
本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;根据各数量之间的关系,正确列出一元一次不等式.
26.【答案】解:;;
恰好是的倍,
,
解得,
的值是;
存在,理由如下:
如图:则,,
,
,
,
解得;
如图:
,
,
,
解得,
综上所述,的值为或.
【解析】
【分析】
本题考查平行线的性质,三角板中交点的特点,掌握平行线的性质并利用分类讨论的思想求解是解题的关键.
根据平行线的性质得到,,再求出,最后根据邻补角互补求出对应角的度数即可;
根据恰好是的倍列方程,计算可求解;
分两种情况,根据画出图形,列方程可解得答案.
【解答】
解:,,
,,
,,
;
见答案;
见答案.
第1页,共1页
一、选择题(本大题共16小题,共32.0分。在每小题列出的选项中,选出符合题目的一项)
1. 可燃冰是一种新型能源,它的密度很小,可燃冰的质量仅为数字用科学记数法表示是( )
A. B. C. D.
2. 已知,下列式子不成立的是( )
A. B. C. D.
3. 如图,某地进行城市规划,在一条新修公路旁有一村庄,现要建一个汽车站,且有,,,四个地点可供选择若要使汽车站离村庄最近,则选择在点处建汽车站的依据是( )
A. 两点之间,线段最短 B. 两点确定一条直线
C. 点到直线的距离 D. 垂线段最短
4. 下列变形中是因式分解的是( )
A. B.
C. D.
5. 山上的一段观光索道如图所示,索道支撑架均为互相平行,且每两个支撑架之间的索道均是直的,若,,则( )
A. B. C. D.
6. 运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了次后就停止,则最小整数值取多少( )
A. B. C. D.
7. 如图,直线,点是直线上一个动点,当点的位置发生变化时,的面积( )
A. 向左移动变小
B. 向右移动变小
C. 始终不变
D. 无法确定
8. 下列命题中的假命题是( )
A. 当时,有
B. 经过已知直线外一点,有且只有一条直线与已知直线平行
C. 互为相反数的两个数的和为
D. 相等的角是对顶角
9. 若、为正整数,则( )
A. B. C. D.
10. 将一副三角尺如图放置,其中,,,则的度数为( )
A.
B.
C.
D.
11. 下面给出的三幅图都是将阴影部分通过割,拼,形成新的图形,其中不能验证平方差公式的是( )
A. B. C. D.
12. 如图,用四颗螺丝将不能弯曲的木条围成一个木框,不计螺丝大小,其中相邻两颗螺丝的距离依次为、、、,且相邻两根木条的夹角均可以调整,若调整木条的夹角时不破坏此木框,则任意两颗螺丝的距离的最大值是( )
A. B. C. D.
13. 如果方程组的解为,那么被“”“”遮住的两个数分别是( )
A. , B. , C. , D. ,
14. 如图,是三位同学证明“三角形内角和是“的三种方案,在证明过程中,没有用“两直线平行,同位角相等”这一理论依据的是( )
方案Ⅰ 方案Ⅱ 方案Ⅲ
过点作,
则,
,
. 过点作,
则,,
. 过点作,
则,,
,
.
A. 方案Ⅰ和方案Ⅱ B. 方案Ⅱ和方案Ⅲ C. 方案Ⅰ和方案Ⅲ D. 都没用到
15. 不等式组的整数解的个数是( )
A. B. C. D.
16. 三角形中,如果一个角是另一个角的倍,这样的三角形我们称之为“灵动三角形”例如,三个内角分别为、、的三角形是“灵动三角形”如图,,
在射线上找一点,过点作交于点,以为端点作射线,交线段于点我们规定.
的度数为;
是“灵动三角形”;
若,则是“灵动三角形”;
当为“灵动三角形”时,为或
结论正确的有个.( )
A. B. C. D.
二、填空题(本大题共3小题,共7.0分)
17. 如图,中,、分别是,的中点,的面积是,则阴影部分的面积是______ .
18. 多项式是一个完全平方式,则______.
19. 要度量作业纸上两条相交直线、所夹锐角的大小,发现其交点不在作业纸内,无法直接度量.
小明的方案:画直线与、相交,如图,测得,,则 ______ 用含、的代数式表示;
小刚的方案:画直线与、相交,再画、相邻的外角的角平分线交于点,如图,则得,则 ______ 用含的代数式表示.
三、解答题(本大题共7小题,共61.0分。解答应写出文字说明,证明过程或演算步骤)
20. 本小题分
计算:;
;
;
因式分解:.
解不等式组,并把它的解集在数轴上表示出来.
解方程组:.
21. 本小题分
在边长为的方格纸中有一个.
作出的高,并求出面积.
将向上平移个单位,再向左平移个单位,得到,请画出.
请任意写出一组平移前后两个三角形中平行且相等的线段.
22. 本小题分
杨老师在黑板上布置了一道题,小白和小红展开了下面的讨论:
已知时,求代数式:的值.
这道题与无关,是可以解的.
只知道的值,没有告诉的值,求不出答案.
根据上述情景,你认为谁说得对?为什么?并求出代数式的值.
23. 本小题分
如图,,,,请将求的过程填写完整.
解:因为
所以____________
又因为
所以______
所以____________
所以____________
因为
所以______
24. 本小题分
发现:任意两个连续奇数的平方差是的倍数.
验证:如,,请求出它的结果是的几倍?
探究:设两个连续奇数为,其中为正整数,请论证“发现”中的结论正确;
延伸:两个连续偶数的平方差是______ 的倍数.
25. 本小题分
某商场计划经销、两种新型节能台灯共盏,这两种台灯的进价、售价如表所示:
型 型
进价元盏
售价元盏
若该商场购进这批台灯共用去元,问这两种台灯各购进多少盏?
在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于元,问至少购进种台灯多少盏?
26. 本小题分
如图,把一块含的直角三角板的边放置于长方形直尺的边上.
如图,现把三角板绕点逆时针旋转,当,且点恰好落在边上时,请直接写出 ______ , ______ 结果用含的代数式表示;
在的条件下,若恰好是的倍,求的值.
如图三角板的放置,现将射线绕点以每秒的转速逆时针旋转得到射线,同时射线绕点以每秒的转速顺时针旋转得到射线,当射线旋转至与重合时,则射线、均停止转动,设旋转时间为在旋转过程中,是否存在,若存在,求出此时的值;若不存在,请说明理由.
答案和解析
1.【答案】
【解析】解:.
故选:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
2.【答案】
【解析】解:,
,
故选项A不符合题意;
,
,
故选项B不符合题意;
,
,
故选项C不符合题意;
,,
,
故选项D符合题意.
故选:.
根据不等式的性质,逐项判断即可.
此题主要考查了不等式的性质:不等式的两边同时乘或除以同一个正数,不等号的方向不变;不等式的两边同时乘或除以同一个负数,不等号的方向改变;不等式的两边同时加上或减去同一个数或同一个含有字母的式子,不等号的方向不变.
3.【答案】
【解析】解:根据题意得:要使汽车站离村庄最近,则选择在点处建汽车站的依据是垂线段最短.
故选:.
根据垂线段最短,即可求解.
本题考查了垂线段最短,熟练掌握垂线段最短的知识点是解此题的关键.
4.【答案】
【解析】解:由因式分解的定义可得,
选项等式右边不是积的形式不是因式分解,不符合题意;
选项是因式分解,符合题意;
选项等式右边不是积的形式不是因式分解,不符合题意;
选项等式右边不是积的形式不是因式分解,不符合题意;
故选:.
根据因式分解的定义:将一个多项式写成几个整式的积的形式,直接判断即可得到答案.
本题考查因式分解的定义:将一个多项式写成几个整式的积的形式叫因式分解.
5.【答案】
【解析】解:如图所示,过点作,
,
,
,,
,
故选:.
如图所示,过点作,则,由平行线的性质进行求解即可.
本题主要考查了平行线的性质,熟知两直线平行,内错角相等是解题的关键.
6.【答案】
【解析】解:依题意,得:,
解得:.
为整数,
的最小值为.
故选:.
根据程序操作进行了次后就停止,即可得出关于的一元一次不等式,解之即可得出的取值范围,再取其中最小的整数值即可得出结论.
本题考查了一元一次不等式的应用,找准等量关系,正确列出一元一次不等式是解题的关键.
7.【答案】
【解析】解:直线,点是直线上一个动点,
无论点怎么移动,点到的距离不变,
的底不变,高不变,面积也不变,
故选:.
根据平行线间的距离处处相等可得点到的距离不变,因此三角形的面积不变.
本题考查平行线间的距离,掌握平行线间的距离处处相等是解题的关键.
8.【答案】
【解析】解:、当时,有,所以为真命题;
B、经过已知直线外一点,有且只有一条直线与已知直线平行,所以为真命题;
C、互为相反数的两个数的和为,所以为真命题;
D、相等的角不一定是对顶角,所以为假命题.
故选D.
根据乘方的意义对进行判断;根据经过已知直线外一点,有且只有一条直线与已知直线平行对进行判断;根据相反数的定义对进行判断;根据对顶角的定义对进行判断.
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果那么”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.
9.【答案】
【解析】解:由题意,原式.
故选:.
依据题意,由乘方的意义及同底数幂的乘法进行计算可以得解.
本题考查了乘方的意义及同底数幂的乘法,需要熟练掌握并理解.
10.【答案】
【解析】解:,
,
,
.
又,
.
故选:.
由,利用“同位角相等,两直线平行”,可得出,利用“两直线平行,同位角相等”,可求出的度数,结合,可求出的度数,再利用邻补角互补,即可求出的度数.
本题考查了平行线的判定与性质以及邻补角,根据各角之间的关系,求出的度数是解题的关键.
11.【答案】
【解析】解:图中,将阴影部分沿着虚线裁剪,可以拼成右侧的平行四边形,
阴影部分面积可以看作两个正方形的面积差,即,所拼成的是底为,高为的平行四边形,因此面积为,所以有,
所以图可以验证平方差公式,不符合题意;
图中阴影部分面积可以看作两个正方形的面积差,即,所拼成的长方形的长为,款为,因此面积为,所以有,
因此图可以验证平方差公式,不符合题意;
图中阴影部分可以看作是边长为的正方形,因此面积为,所拼成的图形中阴影部分的面积可以看作四个小正方形的面积和,,因此不能验证平方差公式,符合题意;
故选:.
根据各个图形中阴影部分面积的“算两次”,进而判断是否验证平方差公式即可.
本题考查平方差公式,掌握平方差公式的结构特征是正确解答的前提,用代数式表示图形中阴影部分的面积是解决问题的关键.
12.【答案】
【解析】解:其中相邻两颗螺丝的距离依次为、、、,
任意两颗螺丝的距离的最大值是,
故选:.
根据三角形的三边关系即可得到结论.
本题考查了三角形的三边关系,熟练掌握三角形的三边关系是解题的关键.
13.【答案】
【解析】解:把代入得,解得,
再把代入得,
故选:.
把代入先求出,再代入求.
本题主要考查了二元一次方程组的解,解题的关键是理解题意,代入法求解.
14.【答案】
【解析】解:方案Ⅰ,过点作,
则两直线平行内错角相等,两直线平行同旁内角互补,
;
方案Ⅱ,过点作,
则两直线平行内错角相等,两直线平行同位角相等,
,
;
方案Ⅲ,过点作,
则两直线平行内错角相等,两直线平行内错角相等,
,
.
方案Ⅰ和方案Ⅲ都没用到“两直线平行,同位角相等”这一理论依据,而方案Ⅱ用到了.
故选:.
根据平行线的性质即可求解.
本题考查了平行线的性质,掌握两直线平行,同位角相等;两直线平行内错角相等;两直线平行同旁内角互补是解题的关键.
15.【答案】
【解析】解:,
解不等式得,
解不等式得.
则不等式组的解集是:.
则整数解是、、,共有个.
故选:.
首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,根据不等式组的解集确定整数解及其个数即可.
此题考查的是一元一次不等式组的解法和一元一次不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
16.【答案】
【解析】解:,
,
,
,
,
是“灵动三角形”,故正确,
,,
,
,
是“灵动三角形”故正确,
是“灵动三角形”,
时,,;
当时,,.
当时,,可得.
综上所述,满足条件的值为或或故错误,
综上所述,正确的有:,共个.
故选:.
根据直角三角形两锐角互余求解.
根据“灵动三角形”的定义判断即可.
根据“灵动三角形”的定义判断即可.
分三种情形,利用三角形内角和定理求解即可.
本题考查三角形内角和定理,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
17.【答案】
【解析】解:是的中点,的面积是,
,
是的中点,
,
故答案为:.
根据三角形中线平分三角形面积进行求解即可.
本题主要考查了三角形中线的性质,熟知三角形中线平分三角形面积是解题的关键.
18.【答案】
【解析】解:是一个完全平方式,
,
故答案为.
根据完全平方公式的灵活应用,这里中间项为减去和的乘积的倍,那么末项是的平方.
本题主要考查完全平方公式,根据两平方项确定出这两个数,再根据乘积二倍项求解.
19.【答案】
【解析】解:,和正好是一个三角形的三个内角,
,
.
故答案为:.
,分别是、的平分线,
,,
,,
即:,,
,,
,
,
,
,
由可知:
故答案为:.
根据,和正好是一个三角形的三个内角,然后根据三角形的内角和定理即可得出答案;
首先根据角平分线的定义得,,再根据邻补角的定义得,,据此得,再根据三角形的内角和定理得可得出,据此可得,然后再利用的结论可得出答案.
此题主要考查了三角形的内角和定理,邻补角的定义,角平分线的定义等,解答此题的关键是熟练掌握三角形的内角和等于.
20.【答案】解:原式
;
原式
;
原式
;
原式
;
,
由得:,
由得:,
不等式组的解集为,
数轴表示如下:
;
,
得:,
解得:,
把代入得:,
解得:,
则方程组的解为.
【解析】原式利用乘方的意义,零指数幂、负整数指数幂法则计算即可求出值;
原式利用幂的乘方运算法则,以及同底数幂的乘除法则计算即可求出值;
原式利用多项式乘多项式,以及单项式乘多项式法则计算,去括号合并即可得到结果;
原式提取公因式,再利用完全平方公式分解即可;
分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,表示在数轴上即可;
方程组利用加减消元法求出解即可.
此题考查了整式的混合运算,提公因式法与公式法的综合运用,解二元一次方程组,实数的运算,以及解一元一次不等式组,熟练掌握各自的解法及运算法则是解本题的关键.
21.【答案】解:高如图所示,.
先将点,,分别向上平移个单位,再向左平移个单位确定点,,,再连接,,,此时即为所求.
与相等且平行,与相等且平行,与相等且平行,三组线段任写一组.
【解析】根据三角形的高的定义画出图形即可.
先将点,,分别向上平移个单位,再向左平移个单位确定点,,,再连接,,,此时即为所求.
利用平移的性质判断即可.
本题考查作图平移变换,平行线的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
22.【答案】解:小红说得对.
理由:
.
化简结果中不含,所以值与取值无关.
所以小红说得对.
当时,
原式.
【解析】利用乘法法则化简给出的代数式,根据化简结果判断谁说得对并求值即可.
本题主要考查了整式的化简求值,掌握整式的乘法公式是解决本题的关键.
23.【答案】 两直线平行,同位角相等 等量代换 内错角相等,两直线平行 两直线平行,同旁内角互补
【解析】解:,
两直线平行,同位角相等,
,
等量代换,
内错角相等,两直线平行,
两直线平行,同旁内角互补,
,
,
故答案为:;两直线平行,同位角相等;等量代换;;内错角相等,两直线平行;;两直线平行,同旁内角互补;.
根据平行线的性质推出,推出,根据平行线的性质得出,代入求出即可.
本题主要考查了平行线的判定与性质,理解平行线的判定与性质进行证明是解此题的关键.
24.【答案】
【解析】解:验证:,
是的倍.
探究:,
两个连续奇数,的平方差是的倍数.
延伸:两个连续偶数的平方差是的倍数.
理由如下:
设两个连续的偶数分别为:,,
,
两个连续偶数的平方差是的倍数.
故答案为:.
验证通过计算即可得出答案;
探究应用因式分解的方法计算,据此可得出结论;
延伸:首先设两个连续的偶数分别为:,,再计算,据此可得出答案.
此题主要考查了因式分解的应用,解答此题的关键是在有理数的运算和整式的运算中熟练应用完全平方公式和平方差公式.
25.【答案】解:设购进种新型节能台灯盏,购进种新型节能台灯盏,
依题意,得:,
解得:.
答:购进种新型节能台灯盏,购进种新型节能台灯盏.
设购进种新型节能台灯盏,则购进种新型节能台灯盏,
依题意,得:,
解得:.
为正整数,
的最小值为.
答:至少购进种台灯盏.
【解析】设购进种新型节能台灯盏,购进种新型节能台灯盏,根据总价单价数量结合该商城用元购进、两种新型节能台灯共盏,即可得出关于,的二元一次方程组,解之即可得出结论;
设购进种新型节能台灯盏,则购进种新型节能台灯盏,根据总利润单盏利润数量结合总利润不少于元,即可得出关于的一元一次不等式,解之取其中的最小整数值即可得出结论.
本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出二元一次方程组;根据各数量之间的关系,正确列出一元一次不等式.
26.【答案】解:;;
恰好是的倍,
,
解得,
的值是;
存在,理由如下:
如图:则,,
,
,
,
解得;
如图:
,
,
,
解得,
综上所述,的值为或.
【解析】
【分析】
本题考查平行线的性质,三角板中交点的特点,掌握平行线的性质并利用分类讨论的思想求解是解题的关键.
根据平行线的性质得到,,再求出,最后根据邻补角互补求出对应角的度数即可;
根据恰好是的倍列方程,计算可求解;
分两种情况,根据画出图形,列方程可解得答案.
【解答】
解:,,
,,
,,
;
见答案;
见答案.
第1页,共1页
同课章节目录
