一元二次方程[上学期]

课件13张PPT。一元二次方程期末复习一一元二次方程的概念 等号两边都是整式, 只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的方程叫做一元二次方程.特点:①都是整式方程;②只含一个未知数;③未知数的最高次数是2.A当 时,它不是一元二次方程.当 时,它是一元二次方程;解： 原方程转化为(2a-4)x2 -2bx+a=0
当a≠2时是一元二次方程；
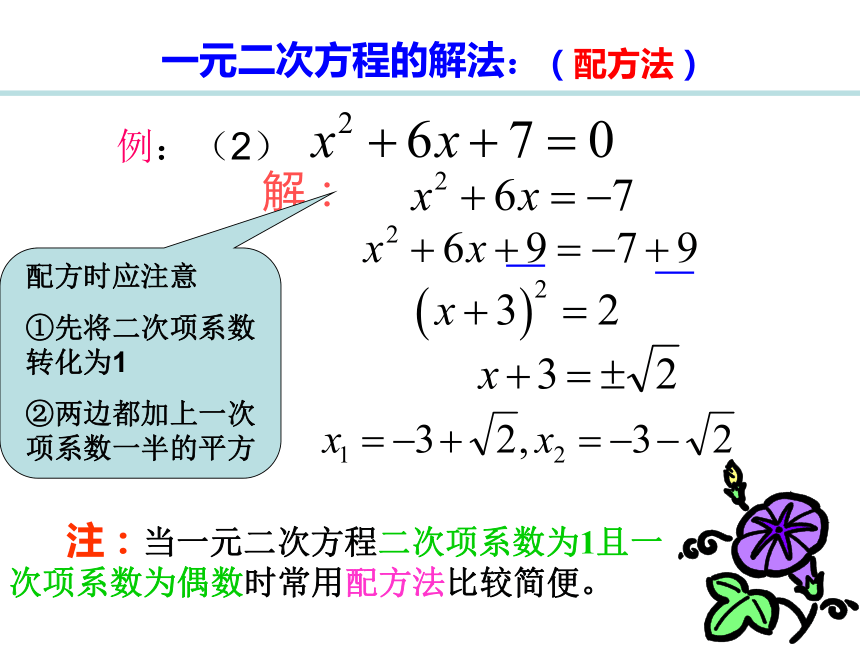
当a＝2,b≠0时是一元一次方程；一元二次方程的一般形式(a,b,c为常数，a≠0）一元二次方程的解法(1)直接开平方法(2)配方法(3)公式法(4)因式分解法例：解下列方程（1）解： 注：当一元二次方程缺一次项时常用直接开平方法。（直接开平方法）一元二次方程的解法：例：（2）一元二次方程的解法：解： 注：当一元二次方程二次项系数为1且一次项系数为偶数时常用配方法比较简便。（配方法）——例：（3）一元二次方程的解法：解：（公式法） 注：当一元二次方程二次项系数为不是1且难以用因式分解时常用公式法比较简便。（因式分解法） 解:原方程化为 （y+2) 2﹣3（y+2）=0
(y+2)(y+2-3)=0
(y+2)(y-1)=0
y+2=0 或 y-1=0
∴y1=-2 y2=1把y+2看作一个整体，变成
a×b=0形式(即两个因式的积的形式)。例：一元二次方程的解法： 注：在解一元二次方程时, 要先观察方程,选择适当的方法.配方法、公式法适用于任何一个一元二次方程,但公式法首先要将方程转化为一般式,而因式分解法只适用于某些一元二次方程.总之它 的基本思路就是将二次方程转化为一次方程,即降次.一元二次方程的根能使方程左右两边相等的未知数的值叫做方程的解，
一元二次方程的解也叫做一元二次方程的根(1).已知x＝－1是方程x2－ax＋6＝0的一个根，则a＝___,另一个根为__
(2).若关于X的一元二次方程
的一个根为0，则 的值为（ ）

A、1 B、-1 C、 1或 -1 D、(3).一元二次方程ax2 +bx +c =0，
若x=1是它的一个根，则a+b+c= ，
若a -b+c=0，则方程必有一根为 。-76B0-1方程有两个不相等的实数根方程有两个相等的实数根方程没有实数根一元二次方程的根的情况不求根,判别一元二次方程 根的情况.所以此方程没有实根.(1).关于x的方程(m-2)x2-4x+4=0有两个实数根.求m的取值范围.关于x的方程(m-2)x2-4x+4=0有两个实数根.求m的取值范围.解:因为方程有两个实数根
所以b2-4ac≥0
即16-16(m-2) ≥0
所以m≤3
因为m≠2
所以m的取值范围是m≤3且m≠2.方程有两个不相等的实数根方程有两个相等的实数根方程没有实数根一元二次方程的根的情况不求根,判别一元二次方程 根的情况.所以此方程没有实根.(2).无论m取何值,关于x的方程x2+mx+2(m+3)=0都有两个实数根吗?为什么?(2).无论m取何值,关于x的方程x2+mx+2(m+3)=0都有两个实数根吗?为什么?解:因为b2-4ac=m2+4×2(m+3)
=m2+8m+24
=(m+4)2+8
因为无论m取何值,(m+4)2≥0
所以 b2-4ac =(m+4)2+8>0
所以无论m取何值,关于x的方程x2+mx+2(m+3)=0
都有两个实数根