人教版九年级上册数学22.3实际问题与二次函数课时训练(含答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 296.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-15 00:00:00 | ||
图片预览

文档简介
人教版九年级上册数学22.3实际问题与二次函数课时训练
一、单选题
1.根据福建省统计局数据,福建省年的地区生产总值为亿元,年的地区生产总值为亿元.设这两年福建省地区生产总值的年平均增长率为x,根据题意可列方程( )
A. B.
C. D.
2.竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+,若小球经过秒落地,则小球在上抛过程中,第( )秒离地面最高.
A. B. C. D.
3.如图,抛物线与轴相交于、两点,与轴相交于点,点在抛物线上,且.与轴相交于点,过点的直线平行于轴,与抛物线交于,两点,则线段的长为( )
A. B.3 C. D.
4.将进货单价为元的某种商品按零售价元一个售出时,每天能卖出个.若这种商品的零售价在一定范围内每降价元,其日销售量就增加个,则能获取的最大利润是( )
A.元 B.元 C.元 D.元
5.某旅社有100张床位,若每张床位每晚收费100元,床位可全部租出,若每张床位每晚收费提高20元,则减少10张床位租出;若每张床位每晚收费再提高20元,则再减少10张床位租出.以每次提高20元的这种方法变化下去,为了投资少而收入最多,每张床位每晚应提高( )
A.60元 B.50元 C.40元 D.40元或60元
6.长方形的周长为24cm,其中一边为xcm(其中 x0),面积为,则这样的长方形中y与x的关系可以写为( )
A. B.
C. D.
7.用20cm长的绳子围成一个矩形,如果这个矩形的一边长为xcm,面积是Scm2,则S与x的函数关系式为( )
A.S=x(20﹣x) B.S=x(20﹣2x) C.S=x(10﹣x) D.S=2x(10﹣x)
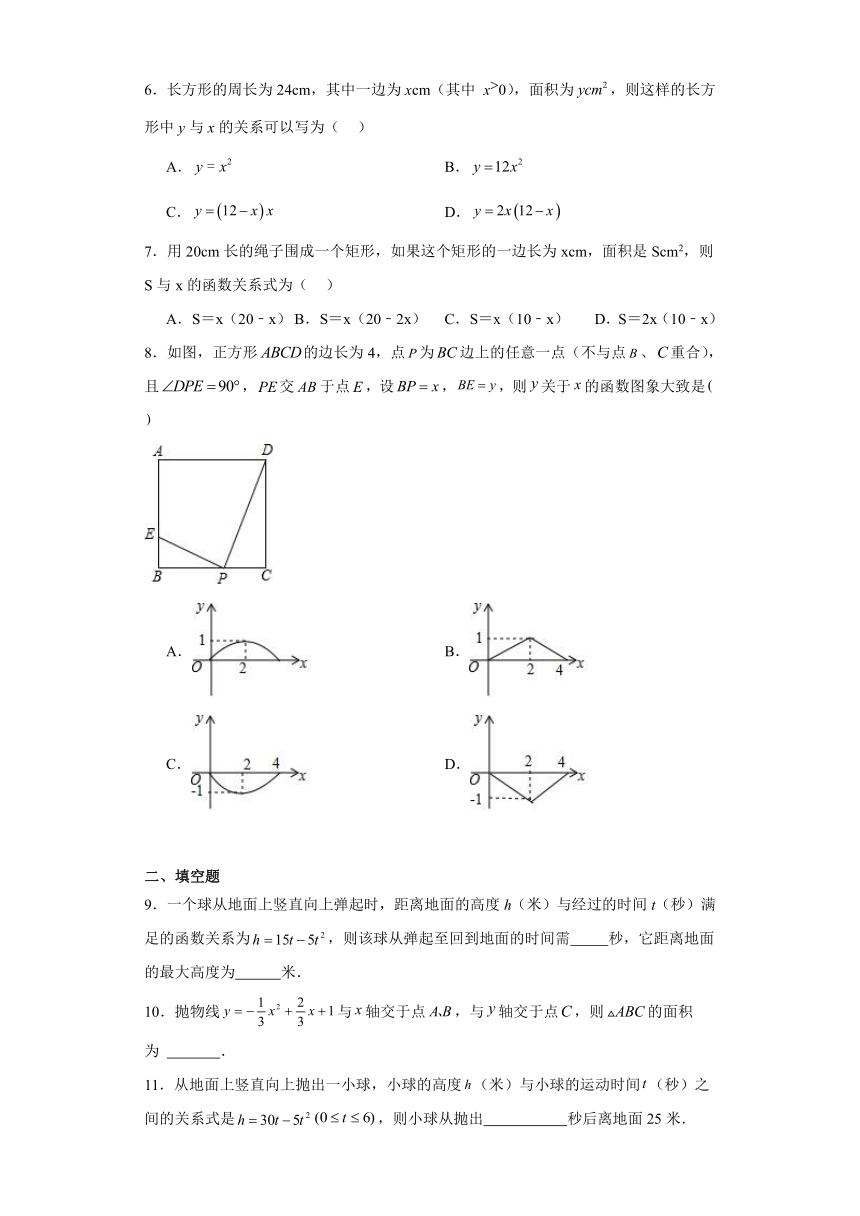
8.如图,正方形的边长为4,点为边上的任意一点(不与点、重合),且,交于点,设,,则关于的函数图象大致是
A. B.
C. D.
二、填空题
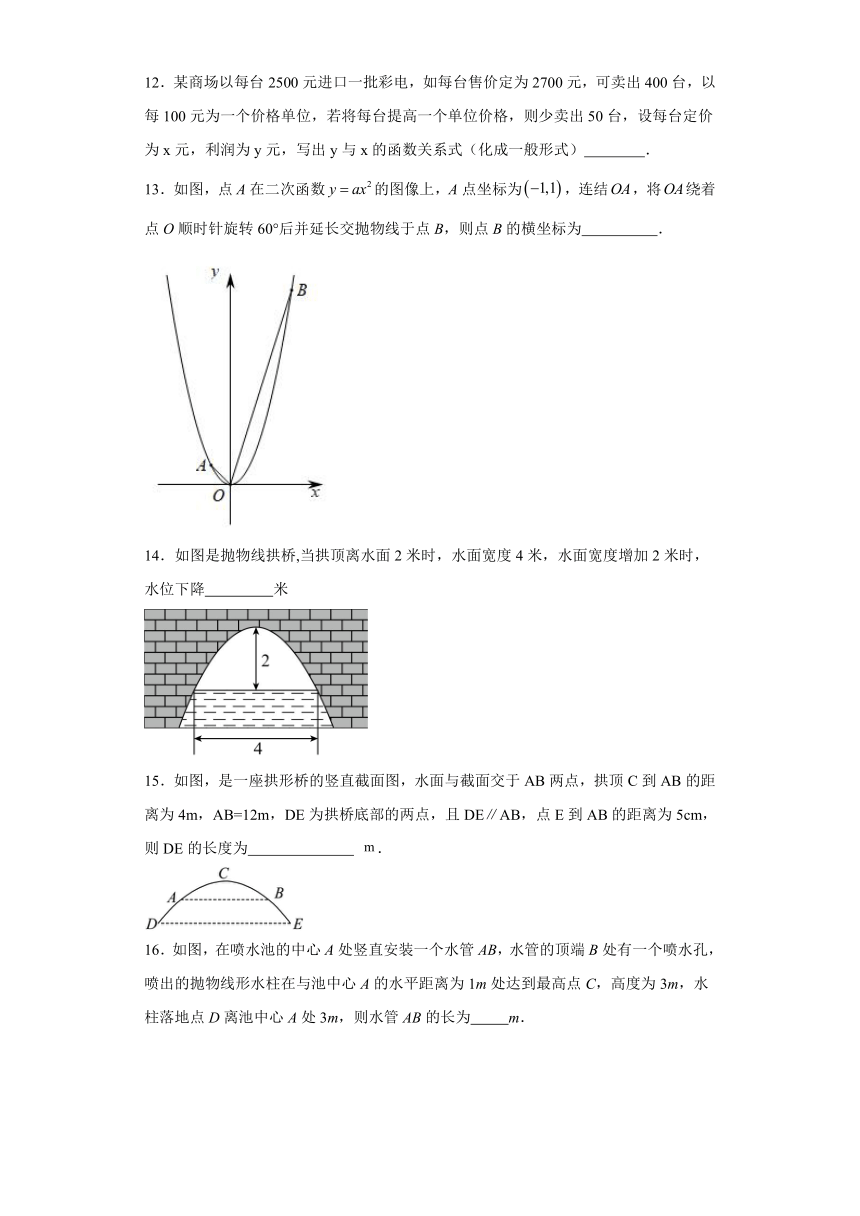
9.一个球从地面上竖直向上弹起时,距离地面的高度h(米)与经过的时间t(秒)满足的函数关系为,则该球从弹起至回到地面的时间需 秒,它距离地面的最大高度为 米.
10.抛物线与轴交于点,与轴交于点,则的面积为 .
11.从地面上竖直向上抛出一小球,小球的高度(米)与小球的运动时间(秒)之间的关系式是,则小球从抛出 秒后离地面25米.
12.某商场以每台2500元进口一批彩电,如每台售价定为2700元,可卖出400台,以每100元为一个价格单位,若将每台提高一个单位价格,则少卖出50台,设每台定价为x元,利润为y元,写出y与x的函数关系式(化成一般形式) .
13.如图,点A在二次函数的图像上,A点坐标为,连结,将绕着点O顺时针旋转60°后并延长交抛物线于点B,则点B的横坐标为 .
14.如图是抛物线拱桥,当拱顶离水面2米时,水面宽度4米,水面宽度增加2米时,水位下降 米
15.如图,是一座拱形桥的竖直截面图,水面与截面交于AB两点,拱顶C到AB的距离为4m,AB=12m,DE为拱桥底部的两点,且DE∥AB,点E到AB的距离为5cm,则DE的长度为 .
16.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端B处有一个喷水孔,喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,则水管AB的长为 m.
三、解答题
17.如图,某市民政局欲给敬老院修建一个半径为米的圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点处安一个喷水头,测得喷水头距地面的高度为,水柱在距喷水头水平距离处达到最高,建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是水柱距喷水头的水平距离,是水柱距地面的高度.
(1)求抛物线的表达式;
(2)请你通过计算说明喷出的水柱是否会落到圆形喷水池的外面.
18.嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点处将沙包(看成点)抛出,并运动路线为抛物线的一部分,淇淇恰在点处接住,然后跳起将沙包回传,其运动路线为抛物线的一部分.
(1)写出的最高点坐标,并求a,c的值;
(2)若嘉嘉在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,求符合条件的n的整数值.
19.为充分利用现有资源,学校“牧春园”计划用一块矩形地种植两种花卉.如图,矩形地一面靠墙(墙的长度为12m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积相等的矩形,已知栅栏的总长度为27m.
(1)若矩形地的面积为,求的长;
(2)当边为多少时,矩形地的面积最大,最大面积是多少
20.某网店销售一种儿童玩具,进价为每件元,物价部门规定每件儿童玩具的售价不低于进价且销售利润不高于进价的.在销售过程中发现,这种儿童玩具每天的销售量y(件)与销售单价x(元)满足一次函数关系.当销售单价为元时,每天的销售量为件;当销售单价为元时,每天的销售量为件.
(1)求y与x之间的函数关系式并直接写出自变量x的取值范围;
(2)若该网店每天想从这种儿童玩具销售中获利元,那么这种儿童玩具的销售单价应定为多少元?
(3)当销售单价为多少元时,该网店销售这种儿童玩具每天获得的利润最大?最大利润是多少元?
参考答案:
1.B
2.A
3.C
4.B
5.A
6.C
7.C
8.A
9. 3
10.2
11.1或5
12.y=﹣5000x2+3000x+80000
13.
14.
15.18
16.
17.(1)
(2)喷出的水柱不会落到圆形喷水池的外面,
18.(1)的最高点坐标为,,;
(2)符合条件的n的整数值为4和5.
19.(1)
(2)时,最大面积是
20.(1),
(2)这种儿童玩具的销售单价应定为元;
(3)当销售单价为元时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是元.
一、单选题
1.根据福建省统计局数据,福建省年的地区生产总值为亿元,年的地区生产总值为亿元.设这两年福建省地区生产总值的年平均增长率为x,根据题意可列方程( )
A. B.
C. D.
2.竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+,若小球经过秒落地,则小球在上抛过程中,第( )秒离地面最高.
A. B. C. D.
3.如图,抛物线与轴相交于、两点,与轴相交于点,点在抛物线上,且.与轴相交于点,过点的直线平行于轴,与抛物线交于,两点,则线段的长为( )
A. B.3 C. D.
4.将进货单价为元的某种商品按零售价元一个售出时,每天能卖出个.若这种商品的零售价在一定范围内每降价元,其日销售量就增加个,则能获取的最大利润是( )
A.元 B.元 C.元 D.元
5.某旅社有100张床位,若每张床位每晚收费100元,床位可全部租出,若每张床位每晚收费提高20元,则减少10张床位租出;若每张床位每晚收费再提高20元,则再减少10张床位租出.以每次提高20元的这种方法变化下去,为了投资少而收入最多,每张床位每晚应提高( )
A.60元 B.50元 C.40元 D.40元或60元
6.长方形的周长为24cm,其中一边为xcm(其中 x0),面积为,则这样的长方形中y与x的关系可以写为( )
A. B.
C. D.
7.用20cm长的绳子围成一个矩形,如果这个矩形的一边长为xcm,面积是Scm2,则S与x的函数关系式为( )
A.S=x(20﹣x) B.S=x(20﹣2x) C.S=x(10﹣x) D.S=2x(10﹣x)
8.如图,正方形的边长为4,点为边上的任意一点(不与点、重合),且,交于点,设,,则关于的函数图象大致是
A. B.
C. D.
二、填空题
9.一个球从地面上竖直向上弹起时,距离地面的高度h(米)与经过的时间t(秒)满足的函数关系为,则该球从弹起至回到地面的时间需 秒,它距离地面的最大高度为 米.
10.抛物线与轴交于点,与轴交于点,则的面积为 .
11.从地面上竖直向上抛出一小球,小球的高度(米)与小球的运动时间(秒)之间的关系式是,则小球从抛出 秒后离地面25米.
12.某商场以每台2500元进口一批彩电,如每台售价定为2700元,可卖出400台,以每100元为一个价格单位,若将每台提高一个单位价格,则少卖出50台,设每台定价为x元,利润为y元,写出y与x的函数关系式(化成一般形式) .
13.如图,点A在二次函数的图像上,A点坐标为,连结,将绕着点O顺时针旋转60°后并延长交抛物线于点B,则点B的横坐标为 .
14.如图是抛物线拱桥,当拱顶离水面2米时,水面宽度4米,水面宽度增加2米时,水位下降 米
15.如图,是一座拱形桥的竖直截面图,水面与截面交于AB两点,拱顶C到AB的距离为4m,AB=12m,DE为拱桥底部的两点,且DE∥AB,点E到AB的距离为5cm,则DE的长度为 .
16.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端B处有一个喷水孔,喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,则水管AB的长为 m.
三、解答题
17.如图,某市民政局欲给敬老院修建一个半径为米的圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点处安一个喷水头,测得喷水头距地面的高度为,水柱在距喷水头水平距离处达到最高,建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中是水柱距喷水头的水平距离,是水柱距地面的高度.
(1)求抛物线的表达式;
(2)请你通过计算说明喷出的水柱是否会落到圆形喷水池的外面.
18.嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点处将沙包(看成点)抛出,并运动路线为抛物线的一部分,淇淇恰在点处接住,然后跳起将沙包回传,其运动路线为抛物线的一部分.
(1)写出的最高点坐标,并求a,c的值;
(2)若嘉嘉在x轴上方的高度上,且到点A水平距离不超过的范围内可以接到沙包,求符合条件的n的整数值.
19.为充分利用现有资源,学校“牧春园”计划用一块矩形地种植两种花卉.如图,矩形地一面靠墙(墙的长度为12m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积相等的矩形,已知栅栏的总长度为27m.
(1)若矩形地的面积为,求的长;
(2)当边为多少时,矩形地的面积最大,最大面积是多少
20.某网店销售一种儿童玩具,进价为每件元,物价部门规定每件儿童玩具的售价不低于进价且销售利润不高于进价的.在销售过程中发现,这种儿童玩具每天的销售量y(件)与销售单价x(元)满足一次函数关系.当销售单价为元时,每天的销售量为件;当销售单价为元时,每天的销售量为件.
(1)求y与x之间的函数关系式并直接写出自变量x的取值范围;
(2)若该网店每天想从这种儿童玩具销售中获利元,那么这种儿童玩具的销售单价应定为多少元?
(3)当销售单价为多少元时,该网店销售这种儿童玩具每天获得的利润最大?最大利润是多少元?
参考答案:
1.B
2.A
3.C
4.B
5.A
6.C
7.C
8.A
9. 3
10.2
11.1或5
12.y=﹣5000x2+3000x+80000
13.
14.
15.18
16.
17.(1)
(2)喷出的水柱不会落到圆形喷水池的外面,
18.(1)的最高点坐标为,,;
(2)符合条件的n的整数值为4和5.
19.(1)
(2)时,最大面积是
20.(1),
(2)这种儿童玩具的销售单价应定为元;
(3)当销售单价为元时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是元.
同课章节目录
