河北省石家庄市正定县2022-2023学年下学期七年级期末数学试卷(含解析)
文档属性
| 名称 | 河北省石家庄市正定县2022-2023学年下学期七年级期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 271.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 17:50:42 | ||
图片预览



文档简介
2022-2023学年河北省石家庄市正定县七年级(下)期末数学试卷
一、选择题(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2分)下列方程:
①x2+y2=1;
②;
③2x+3y=0;
④;
其中二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
2.(2分)我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为( )
A.7.5×105 B.7.5×10﹣5 C.0.75×10﹣4 D.75×10﹣6
3.(2分)如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( )
A. B.
C. D.
4.(2分)下列等式从左到右的变形,属于因式分解的是( )
A.a(x﹣y)=ax﹣ay B.x3﹣x=x(x+1)(x﹣1)
C.(x+1)(x+3)=x2+4x+3 D.x2+2x+1=x(x+2)+1
5.(2分)如果a=﹣0.32,b=﹣3﹣2,c=(﹣)﹣2,d=(﹣)0,那么a、b、c、d的大小关系为( )
A.a<b<c<d B.a<d<c<b C.b<a<d<c D.c<a<d<b
6.(2分)如果关于x的不等式2x+a>0的解集在数轴上表示如下图,那么a的值为( )
A.﹣2 B.2 C.﹣6 D.6
7.(2分)方程组中,若未知数x、y满足x+y>0,则m的取值范围是( )
A.m>﹣4 B.m≥﹣4 C.m<﹣4 D.m≤﹣4
8.(2分)已知是方程2x﹣ay=3的一个解,那么a的值是( )
A.1 B.3 C.﹣3 D.﹣1
9.(2分)下列式子一定成立的是( )
A.若ac2=bc2,则a=b
B.若ac>bc,则a>b
C.若a>b,则ac>bc2
D.若a<b,则a(c2+1)<b(c2+1)
10.(2分)已知方程组和有相同的解,则a,b的值为( )
A. B. C. D.
11.(2分)如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
12.(2分)如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )
A.70° B.50° C.40° D.30°
13.(2分)我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
14.(2分)已知关于x的不等式组的整数解共有5个,则a的取值范围是( )
A.﹣3<a<﹣2 B.﹣3<a≤﹣2 C.﹣3≤a≤﹣2 D.﹣3≤a<﹣2
15.(2分)如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为( )
A.20° B.30° C.40° D.无法确定
16.(2分)如图,在△ABC 中,点D、E、F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是( )
A.30 B.28 C.56 D.60
二、填空题(共4小题,17-19题每题3分,20题每空2分,共13分)
17.(3分)因式分解:a2﹣2ab+b2﹣1= .
18.(3分)自来水公司为某小区A改造供水系统,如图沿路线AO铺设管道和BO主管道衔接(AO⊥BO),路线最短,工程造价最低,根据是 .
19.(3分)如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数 .
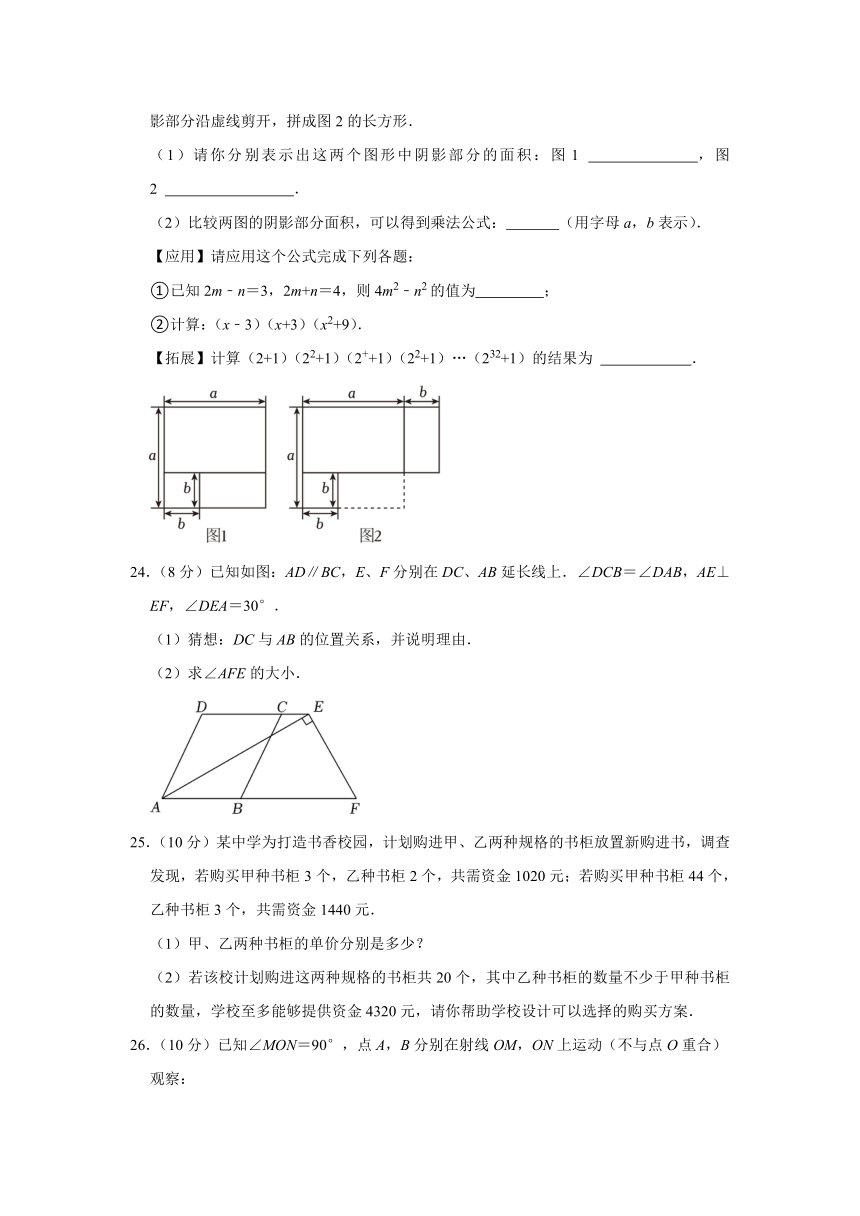
20.(4分)在△ABC中,∠A=160°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图①,则∠A1的度数为 ;第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图②.照此下去,至多能进行 步.
三、解答题(本大题共6个大题,共55分,解答应写出文字说明、证明过程或演算步骤)
21.(10分)(1)解方程组:;
(2)解不等式组并写出不等式组的整数解.
22.(10分)(1)先化简,再求值:a(a﹣3b)+(a+b)2﹣a(a﹣b)其中a=1,.
(2)是小明完成的一道作业,请你参考小明的方法解答下面的问题:
小明的作业计算:85×(﹣0.125)5 解:85×(﹣0.125)5=(﹣8×0.125)5 =(﹣1)5 =﹣1
①42020×(﹣0.25)2020;
②;
③若 2×4n×16n=219,直接写出n的值.
23.(7分)边长为b的小1,从边长为a的大正方形中剪掉一个【探究】如图1方形,将阴影部分沿虚线剪开,拼成图2的长方形.
(1)请你分别表示出这两个图形中阴影部分的面积:图1 ,图2 .
(2)比较两图的阴影部分面积,可以得到乘法公式: (用字母a,b表示).
【应用】请应用这个公式完成下列各题:
①已知2m﹣n=3,2m+n=4,则4m2﹣n2的值为 ;
②计算:(x﹣3)(x+3)(x2+9).
【拓展】计算(2+1)(22+1)(2++1)(22+1)…(232+1)的结果为 .
24.(8分)已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
(1)猜想:DC与AB的位置关系,并说明理由.
(2)求∠AFE的大小.
25.(10分)某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需资金1020元;若购买甲种书柜44个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜的单价分别是多少?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请你帮助学校设计可以选择的购买方案.
26.(10分)已知∠MON=90°,点A,B分别在射线OM,ON上运动(不与点O重合)
观察:
(1)如图1,若∠OBA和∠OAB的平分线交于点C,∠ACB= °
猜想:
(2)如图2,随着点A,B分别在射线OM,ON上运动(不与点O重合).若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E,∠E的大小会变吗?如果不会,求∠E的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将△ABE沿MN折叠,使点E落在四边形ABMN内点E′的位置.求∠BME′+∠ANE′的度数.
2022-2023学年河北省石家庄市正定县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2分)下列方程:
①x2+y2=1;
②;
③2x+3y=0;
④;
其中二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
【分析】利用二元一次方程的定义,逐一分析给出的四个方程即可.
【解答】解:∵①方程x2+y2=1是二元二次方程;②方程3x+=4是分式方程;③方程2x+3y=0是二元一次方程;④方程+=7是二元一次方程,
∴二元一次方程有2个.
故选:B.
本题考查了二元一次方程的定义,牢记“含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程”是解题的关键.
2.(2分)我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为( )
A.7.5×105 B.7.5×10﹣5 C.0.75×10﹣4 D.75×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:将0.000075用科学记数法表示为:7.5×10﹣5.
故选:B.
本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
3.(2分)如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( )
A. B.
C. D.
【分析】根据高线的定义即可得出结论.
【解答】解:A,C,D都不是△ABC的边AB上的高,
故选:B.
本题考查的是作图﹣基本作图,熟知三角形高线的定义是解答此题的关键.
4.(2分)下列等式从左到右的变形,属于因式分解的是( )
A.a(x﹣y)=ax﹣ay B.x3﹣x=x(x+1)(x﹣1)
C.(x+1)(x+3)=x2+4x+3 D.x2+2x+1=x(x+2)+1
【分析】根据因式分解的意义即可判断.
【解答】解:因式分解是指将一个多项式化为几个整式的乘积,
故选:B.
本题考查因式分解的意义,解题的关键是正确理解因式分解的意义,本题属于基础题型.
5.(2分)如果a=﹣0.32,b=﹣3﹣2,c=(﹣)﹣2,d=(﹣)0,那么a、b、c、d的大小关系为( )
A.a<b<c<d B.a<d<c<b C.b<a<d<c D.c<a<d<b
【分析】根据负整数指数幂、有理数的乘方、零指数幂的定义将a、b、c、d的值计算出来即可比较出其值的大小.
【解答】解:因为a=﹣0.32=﹣0.09,
b=﹣3﹣2=﹣=﹣,
c=(﹣)﹣2==9,
d=(﹣)0=1,
所以c>d>a>b.
故选:C.
本题主要考查了
(1)零指数幂,负整数指数幂和有理数的乘方运算:负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
(2)有理数比较大小:正数>0;0>负数;两个负数,绝对值大的反而小.
6.(2分)如果关于x的不等式2x+a>0的解集在数轴上表示如下图,那么a的值为( )
A.﹣2 B.2 C.﹣6 D.6
【分析】先根据在数轴上表示不等式解集的方法得出不等式的解集,再把a当作已知条件得出不等式的解集,与求出的不等式解集相比较即可.
【解答】解:∵由题意可知,不等式的解集为x>3,
解不等式2x+a>0得,x>﹣,
∴﹣=3,解得a=﹣6.
故选:C.
本题考查的是解一元一次不等式,熟知不等式的基本性质是解答此题的关键.
7.(2分)方程组中,若未知数x、y满足x+y>0,则m的取值范围是( )
A.m>﹣4 B.m≥﹣4 C.m<﹣4 D.m≤﹣4
【分析】①+②得出3x+3y=4+m,求出x+y=,根据x+y>0得出>0,再求出不等式的解集即可.
【解答】解:,
①+②,得3x+3y=4+m,
x+y=,
∵方程组中,未知数x、y满足x+y>0,
∴>0,
解得:m>﹣4,
故选:A.
本题考查了解二元一次方程组,二元一次方程组的解和解一元一次不等式等知识点,能求出关于m的不等式是解此题的关键.
8.(2分)已知是方程2x﹣ay=3的一个解,那么a的值是( )
A.1 B.3 C.﹣3 D.﹣1
【分析】把方程的解代入方程,把关于x和y的方程转化为关于a的方程,然后解方程即可.
【解答】解:∵是方程2x﹣ay=3的一个解,
∴满足方程2x﹣ay=3,
∴2×1﹣(﹣1)a=3,即2+a=3,
解得a=1.
故选:A.
本题主要考查了二元一次方程的解.解题关键是把方程的解代入原方程,使原方程转化为以系数a为未知数的方程.
9.(2分)下列式子一定成立的是( )
A.若ac2=bc2,则a=b
B.若ac>bc,则a>b
C.若a>b,则ac>bc2
D.若a<b,则a(c2+1)<b(c2+1)
【分析】根据不等式的性质进行判断即可.
【解答】解:A.若c=0,则ac2=bc2,
但a与b不一定相等,
则A不符合题意;
B.若ac>bc,c<0,
那么a<b,
则B不符合题意;
C.若a>b,c=0,
那么ac=bc2,
则C不符合题意;
D.若a<b,则c2+1>0,
那么a(c2+1)<b(c2+1),
则D符合题意;
故选:D.
本题考查不等式的性质,根据不等式的性质并结合反例进行判断是解题的关键.
10.(2分)已知方程组和有相同的解,则a,b的值为( )
A. B. C. D.
【分析】因为方程组和有相同的解,所以把5x+y=3和x﹣2y=5联立解之求出x、y,再代入其他两个方程即可得到关于a、b的方程组,解方程组即可求解.
【解答】解:∵方程组和有相同的解,
∴方程组的解也它们的解,
解得:,
代入其他两个方程得,
解得:,
故选:D.
本题主要考查了二元一次方程的解及二元一次方程组的解法,正确理解题意,然后根据题意得到关于待定系数的方程组,解方程组是解答此题的关键.
11.(2分)如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
【分析】根据平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行分别进行分析即可.
【解答】解:A、根据内错角相等,两直线平行可判断直线l1∥l2,故此选项不合题意;
B、∠2=∠3,不能判断直线l1∥l2,故此选项符合题意;
C、根据同位角相等,两直线平行可判断直线l1∥l2,故此选项不合题意;
D、根据同旁内角互补,两直线平行可判断直线l1∥l2,故此选项不合题意;
故选:B.
此题主要考查了平行线的判定,关键是掌握平行线的判定定理.
12.(2分)如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )
A.70° B.50° C.40° D.30°
【分析】延长ED交BC于F,根据平行线的性质求出∠MFC=∠ABC=70°,求出∠FDC=30°,根据三角形外角性质得出∠BCD=∠MFC﹣∠MDC,代入求出即可.
【解答】解:延长ED交BC于F,如图所示:
∵AB∥DE,∠ABC=70°,
∴∠MFC=∠ABC=70°,
∵∠CDE=140°,
∴∠FDC=180°﹣140°=30°,
∴∠BCD=∠MFC﹣∠MDC=70°﹣30°=40°,
故选:C.
本题考查了三角形外角性质,平行线的性质,解此题的关键是求出∠MFC的度数,注意:两直线平行,同位角相等.
13.(2分)我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
【分析】直接利用“绳长=木条+4.5;绳子=木条﹣1”分别得出等式求出答案.
【解答】解:设木条长x尺,绳子长y尺,那么可列方程组为:
.
故选:A.
此题主要考查了由实际问题抽象出二元一次方程组,正确得出等量关系是解题关键.
14.(2分)已知关于x的不等式组的整数解共有5个,则a的取值范围是( )
A.﹣3<a<﹣2 B.﹣3<a≤﹣2 C.﹣3≤a≤﹣2 D.﹣3≤a<﹣2
【分析】先求出每个不等式的解集,再求出不等式组的解集,根据已知得出关于a的不等式组,即可得出选项.
【解答】解:
∵解不等式①得:x≥a,
解不等式②得:x<3,
∴不等式组的解集为a≤x<3,
∵关于x的不等式组的整数解共有5个,
∴﹣3<a≤﹣2,
故选:B.
本题考查了解一元一次不等式组,不等式组的整数解的应用,解此题的关键是能根据不等式组的解集和已知得出关于a的不等式组.
15.(2分)如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为( )
A.20° B.30° C.40° D.无法确定
【分析】先根据三角形内角和定理求出∠C的度数,故可得出∠3+∠4的度数,根据四边形的内角和等于360°即可得出结论.
【解答】解:∵△ABC中,∠A=60°∠B=70°,∠2=80°,
∴∠C=180°﹣60°﹣70°=50°,
∴∠3+∠4=∠A+∠B=60°+70°=130°,
∴∠1=360°﹣(∠A+∠B)﹣(∠3+∠4)﹣∠2=360°﹣130°﹣130°﹣80°=20°.
故选:A.
本题考查的是三角形内角和定理及翻折变换,熟知图形翻折不变性的性质是解答此题的关键.
16.(2分)如图,在△ABC 中,点D、E、F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是( )
A.30 B.28 C.56 D.60
【分析】根据BD=2DC得出△BGD和△CGD面积之间的关系,根据E是AC的中点得出△AGE和△CGE面积之间的关系,从而求出△BCE的面积,再根据BE是△ABC的中线即可求出△ABC的面积.
【解答】解:∵BD=2DC,
∴S△BGD=2S△CGD=16,
∴S△CGD=8,
∵E是AC的中点,
∴S△AGE=S△CGE=6,
∴S△BCE=S△BGD+S△CGD+S△CGE
=16+8+6
=30,
∵E是AC的中点,
∴S△ABC=2S△BCE=2×30=60,
故选:D.
本题考查了三角形面积的求法,熟知三角形的中线把三角形分成两个面积相等的三角形.
二、填空题(共4小题,17-19题每题3分,20题每空2分,共13分)
17.(3分)因式分解:a2﹣2ab+b2﹣1= (a﹣b+1)(a﹣b﹣1) .
【分析】先将该多项式分组,再运用公式法进行因式分解.
【解答】解:a2﹣2ab+b2﹣1
=(a2﹣2ab+b2)﹣1
=(a﹣b)2﹣12
=(a﹣b+1)(a﹣b﹣1),
故答案为:(a﹣b+1)(a﹣b﹣1).
此题考查了运用分组法和公式法进行因式分解的能力,关键是能准确确定分解方法.
18.(3分)自来水公司为某小区A改造供水系统,如图沿路线AO铺设管道和BO主管道衔接(AO⊥BO),路线最短,工程造价最低,根据是 垂线段最短 .
【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.据此作答.
【解答】解:根据是:直线外一点与直线上各点连接而得到的所有线段中,垂线段最短.
故答案为:垂线段最短.
此题主要考查垂线段最短在实际生活中的应用.
19.(3分)如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数 60° .
【分析】由垂直的定义,角平分线的定义以及三角形内角和定理进行计算即可.
【解答】解:∵AD⊥BC,
∴∠ADB=90°,
∵∠B=50°,
∴∠BAD=90°﹣50°=40°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=40°﹣5°=35°,
∴∠BAC=2×35°=70°,
∴∠C=180°﹣50°﹣70°
=60°,
故答案为:60°.
本题考查三角形内角和定理,角平分线以及垂直的定义,掌握三角形内角和是180°,角平分线的定义是正确解答的前提.
20.(4分)在△ABC中,∠A=160°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图①,则∠A1的度数为 140° ;第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图②.照此下去,至多能进行 7 步.
【分析】根据三角形内角和是180°,推出另外两角之和,依次类推可得出规律,依据三角形角不能为0,推出进行的步数即可.
【解答】解:∵∠A=160°,
∴∠ABC+∠ACB=180°﹣∠A=20°,
∵∠A1BA=∠ABC,∠A1CA=∠ACB,
∴∠A1BC+∠A1CB=2(∠ABC+∠ACB)=40°,
∴∠A1=180°﹣(∠A1BC+∠A1CB)=140°,
同理∠A2=120°,
∠A3=100°,
……
∠An=180°﹣20(n+1),
∴当n=8时,∠A8=0,
∴至多能进行七步.
故答案为:140°,7.
本题考查了三角形的内角和定理,三角形内角和是180°,知道一个角的度数,可以求出另外两角和的度数.
三、解答题(本大题共6个大题,共55分,解答应写出文字说明、证明过程或演算步骤)
21.(10分)(1)解方程组:;
(2)解不等式组并写出不等式组的整数解.
【分析】(1)利用加减消元法求解即可;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集,即可求出整数解.
【解答】解:(1)①×2+②,得:11x=22,
解得x=2,
将x=2代入①,得:8﹣y=5,
解得y=3,
∴方程组的解为;
(2)解不等式+3≥x,得:x≤3,
解不等式1﹣2(x﹣1)<4﹣x,得:x>﹣1,
则不等式组的解集为﹣1<x≤3,
所以不等式组的整数解为0,1,2,3.
本题考查的是解二元一次方程组和一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
22.(10分)(1)先化简,再求值:a(a﹣3b)+(a+b)2﹣a(a﹣b)其中a=1,.
(2)是小明完成的一道作业,请你参考小明的方法解答下面的问题:
小明的作业计算:85×(﹣0.125)5 解:85×(﹣0.125)5=(﹣8×0.125)5 =(﹣1)5 =﹣1
①42020×(﹣0.25)2020;
②;
③若 2×4n×16n=219,直接写出n的值.
【分析】(1)先展开,再去括号,合并同类项,化简后将a,b的值代入计算即可;
(2)①逆用积的乘方法则可得答案;
②逆用积的乘方法则;
③化为同底数,可得关于n的方程,即可解得答案.
【解答】解:(1)原式=a2﹣3ab+a2+2ab+b2﹣a2+ab
=a2+b2,
当a=1,b=﹣时,
原式=12+(﹣)2
=1+
=;
(2)①42020×(﹣0.25)2020
=[4×(﹣0.25)]2020
=(﹣1)2020
=1;
②原式=[×(﹣)×]11×(﹣)2×
=(﹣1)11××
=﹣1××
=﹣;
③∵2×4n×16n=219,
∴2×22n×24n=219;
∴26n+1=219;
∴6n+1=19,
解得n=3,
∴n的值为3.
本题考查整式的混合运算,解题的关键是掌握整式相关运算的法则.
23.(7分)边长为b的小1,从边长为a的大正方形中剪掉一个【探究】如图1方形,将阴影部分沿虚线剪开,拼成图2的长方形.
(1)请你分别表示出这两个图形中阴影部分的面积:图1 a2﹣b2 ,图2 (a+b)(a﹣b) .
(2)比较两图的阴影部分面积,可以得到乘法公式: 1 (用字母a,b表示).
【应用】请应用这个公式完成下列各题:
①已知2m﹣n=3,2m+n=4,则4m2﹣n2的值为 12 ;
②计算:(x﹣3)(x+3)(x2+9).
【拓展】计算(2+1)(22+1)(2++1)(22+1)…(232+1)的结果为 264﹣1 .
【分析】(1)图①阴影部分的面积为两个正方形的面积差,即a2﹣b2,而图②的阴影部分为长为(a+b),宽为(a﹣b)的矩形,可表示出面积为(a+b)(a﹣b).
(2)由图①与图②的面积相等,可以得到乘法公式;
①利用公式将4m2﹣n2写成(2m﹣n)(2m+n)进而求出答案.
②连续两次利用平方差公式进行计算即可.
将原式转化为(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1),再连续使用平方差公式,得出最后的结果.
【解答】解:【探究】(1)图①阴影部分的面积为两个正方形的面积差,即a2﹣b2;图②的阴影部分为长为(a+b),宽为(a﹣b)的矩形,其面积为(a+b)(a﹣b).
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)由图①与图②的面积相等,可以得到乘法公式,(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b);(a﹣b)=a2﹣b2;
【应用】①4m2﹣n2=(2m﹣n)(2m+n)=3×4=12.
故答案为:12.
②(x﹣3)(x+3)(x2+9)=(x2﹣9)(x2+9)=x4﹣81;
【拓展】(2+1)(22+1)(24+1)(28+1)…(232+1),
=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1),
=(22﹣1)(22+1)(24+1)(28+1)…(232+1),
=(24﹣1)(24+1)(28+1)…(232+1),
=(28﹣1)(28+1)…(232+1),
=264﹣1.
故答案为:264﹣1.
考查平方差公式,掌握平方差公式的结构特征是正确应用的前提.
24.(8分)已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
(1)猜想:DC与AB的位置关系,并说明理由.
(2)求∠AFE的大小.
【分析】(1)由AD∥BC,得到∠CBF=∠DAB,而∠DCB=∠DAB,因此∠CBF=∠DCB,即可证明CD∥AB;
(2)由DC∥AB,得到∠EAF=∠DEA=30°,由直角三角形的性质得到∠AFE=90°﹣∠EAF=60°.
【解答】解:(1)CD∥AB,理由如下:
∵AD∥BC,
∴∠CBF=∠DAB,
∵∠DCB=∠DAB,
∵∠CBF=∠DCB,
∴CD∥AB;
(2)∵DC∥AB,
∴∠EAF=∠DEA=30°,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AFE=90°﹣∠EAF=60°.
本题考查平行线的判定和性质,熟练掌握平行线的判定和性质是解题的关键.
25.(10分)某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需资金1020元;若购买甲种书柜44个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜的单价分别是多少?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请你帮助学校设计可以选择的购买方案.
【分析】(1)设每个甲种书柜的价格是x元,每个乙种书柜的价格是y元,根据“若购买甲种书柜3个,乙种书柜2个,共需要资金1020元;若购买甲种书柜4个,乙种书柜3个,共需要资金1440元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买m个甲种书柜,则购买(20﹣m)个乙种书柜,根据“乙种书柜的数量不少于甲种书柜的数量,且学校至多能提供资金4320元”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数,即可得出各购买方案.
【解答】解:(1)设每个甲种书柜的单价是x元,每个乙种书柜的单价是y元,
依题意得:,
解得:.
答:甲种书柜的单价是180元,乙种书柜的单价是240元.
(2)设购买m个甲种书柜,则购买(20﹣m)个乙种书柜,
依题意得:,
解得:8≤m≤10,
又∵m为整数,
∴m可以取8,9,10,
∴该校共有3种购买方案,
方案1:购买8个甲种书柜,12个乙种书柜;
方案2:购买9个甲种书柜,11个乙种书柜;
方案3:购买10个甲种书柜,10个乙种书柜.
本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
26.(10分)已知∠MON=90°,点A,B分别在射线OM,ON上运动(不与点O重合)
观察:
(1)如图1,若∠OBA和∠OAB的平分线交于点C,∠ACB= 135 °
猜想:
(2)如图2,随着点A,B分别在射线OM,ON上运动(不与点O重合).若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E,∠E的大小会变吗?如果不会,求∠E的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将△ABE沿MN折叠,使点E落在四边形ABMN内点E′的位置.求∠BME′+∠ANE′的度数.
【分析】(1)根据三角形的内角和定理角平分线的定义计算即可.
(2)利用三角形的外角的性质,三角形内角和定理构建关系式解决问题即可.
(3)根据翻折不变性,三角形内角和定理,三角形的外角的性质构建关系式解决问题即可.
【解答】解:观察:(1)∵∠MON=90°,
∴∠OAB+∠OBA=90°,
∵∠OBA和∠OAB的平分线交于点C,
∴∠ABC=∠OBA,∠BAC=∠OAB,
∴∠ABC+∠BAC=(∠OBA+∠OAB)=45°,
∴∠CBA=180°﹣45°=135°
故答案为135.
猜想:(2)∵AE是∠BAO的平分线
∴∠BAE=∠BAO,
∵BC是∠ABN的平分线,
∴∠CBA=∠NBA,
∵∠NBA=∠O+∠BAO,
∴∠CBA=(∠O+∠BAO)=45°+∠BAE,
∵∠CBA=∠E+∠BAE,
∴∠E+∠BAE=45°+∠BAE,
即∠E=45°.
拓展:(3)由折叠可得,∠EMN=∠E′MN,∠E N M=∠E′NM,
∴2∠EMN+∠BM E′=180°,2∠ENM+∠ANE′=180°,
∴∠BM E′=180°﹣2∠EMN,∠ANE′=180°﹣2∠ENM,
∴∠BM E′+∠ANE′=360°﹣2(∠EMN+∠ENM),
∵∠EMN+∠ENM=180°﹣∠E,∠E=45°,
∴∠BM E′+∠ANE′=360°﹣2(∠EMN+∠ENM)
=360°﹣2(180°﹣∠E)
=2∠E
=90°.
本题考查三角形内角和定理,三角形的外角的性质,翻折变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
一、选择题(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2分)下列方程:
①x2+y2=1;
②;
③2x+3y=0;
④;
其中二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
2.(2分)我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为( )
A.7.5×105 B.7.5×10﹣5 C.0.75×10﹣4 D.75×10﹣6
3.(2分)如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( )
A. B.
C. D.
4.(2分)下列等式从左到右的变形,属于因式分解的是( )
A.a(x﹣y)=ax﹣ay B.x3﹣x=x(x+1)(x﹣1)
C.(x+1)(x+3)=x2+4x+3 D.x2+2x+1=x(x+2)+1
5.(2分)如果a=﹣0.32,b=﹣3﹣2,c=(﹣)﹣2,d=(﹣)0,那么a、b、c、d的大小关系为( )
A.a<b<c<d B.a<d<c<b C.b<a<d<c D.c<a<d<b
6.(2分)如果关于x的不等式2x+a>0的解集在数轴上表示如下图,那么a的值为( )
A.﹣2 B.2 C.﹣6 D.6
7.(2分)方程组中,若未知数x、y满足x+y>0,则m的取值范围是( )
A.m>﹣4 B.m≥﹣4 C.m<﹣4 D.m≤﹣4
8.(2分)已知是方程2x﹣ay=3的一个解,那么a的值是( )
A.1 B.3 C.﹣3 D.﹣1
9.(2分)下列式子一定成立的是( )
A.若ac2=bc2,则a=b
B.若ac>bc,则a>b
C.若a>b,则ac>bc2
D.若a<b,则a(c2+1)<b(c2+1)
10.(2分)已知方程组和有相同的解,则a,b的值为( )
A. B. C. D.
11.(2分)如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
12.(2分)如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )
A.70° B.50° C.40° D.30°
13.(2分)我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
14.(2分)已知关于x的不等式组的整数解共有5个,则a的取值范围是( )
A.﹣3<a<﹣2 B.﹣3<a≤﹣2 C.﹣3≤a≤﹣2 D.﹣3≤a<﹣2
15.(2分)如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为( )
A.20° B.30° C.40° D.无法确定
16.(2分)如图,在△ABC 中,点D、E、F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是( )
A.30 B.28 C.56 D.60
二、填空题(共4小题,17-19题每题3分,20题每空2分,共13分)
17.(3分)因式分解:a2﹣2ab+b2﹣1= .
18.(3分)自来水公司为某小区A改造供水系统,如图沿路线AO铺设管道和BO主管道衔接(AO⊥BO),路线最短,工程造价最低,根据是 .
19.(3分)如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数 .
20.(4分)在△ABC中,∠A=160°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图①,则∠A1的度数为 ;第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图②.照此下去,至多能进行 步.
三、解答题(本大题共6个大题,共55分,解答应写出文字说明、证明过程或演算步骤)
21.(10分)(1)解方程组:;
(2)解不等式组并写出不等式组的整数解.
22.(10分)(1)先化简,再求值:a(a﹣3b)+(a+b)2﹣a(a﹣b)其中a=1,.
(2)是小明完成的一道作业,请你参考小明的方法解答下面的问题:
小明的作业计算:85×(﹣0.125)5 解:85×(﹣0.125)5=(﹣8×0.125)5 =(﹣1)5 =﹣1
①42020×(﹣0.25)2020;
②;
③若 2×4n×16n=219,直接写出n的值.
23.(7分)边长为b的小1,从边长为a的大正方形中剪掉一个【探究】如图1方形,将阴影部分沿虚线剪开,拼成图2的长方形.
(1)请你分别表示出这两个图形中阴影部分的面积:图1 ,图2 .
(2)比较两图的阴影部分面积,可以得到乘法公式: (用字母a,b表示).
【应用】请应用这个公式完成下列各题:
①已知2m﹣n=3,2m+n=4,则4m2﹣n2的值为 ;
②计算:(x﹣3)(x+3)(x2+9).
【拓展】计算(2+1)(22+1)(2++1)(22+1)…(232+1)的结果为 .
24.(8分)已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
(1)猜想:DC与AB的位置关系,并说明理由.
(2)求∠AFE的大小.
25.(10分)某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需资金1020元;若购买甲种书柜44个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜的单价分别是多少?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请你帮助学校设计可以选择的购买方案.
26.(10分)已知∠MON=90°,点A,B分别在射线OM,ON上运动(不与点O重合)
观察:
(1)如图1,若∠OBA和∠OAB的平分线交于点C,∠ACB= °
猜想:
(2)如图2,随着点A,B分别在射线OM,ON上运动(不与点O重合).若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E,∠E的大小会变吗?如果不会,求∠E的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将△ABE沿MN折叠,使点E落在四边形ABMN内点E′的位置.求∠BME′+∠ANE′的度数.
2022-2023学年河北省石家庄市正定县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共16个小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2分)下列方程:
①x2+y2=1;
②;
③2x+3y=0;
④;
其中二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
【分析】利用二元一次方程的定义,逐一分析给出的四个方程即可.
【解答】解:∵①方程x2+y2=1是二元二次方程;②方程3x+=4是分式方程;③方程2x+3y=0是二元一次方程;④方程+=7是二元一次方程,
∴二元一次方程有2个.
故选:B.
本题考查了二元一次方程的定义,牢记“含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程”是解题的关键.
2.(2分)我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为( )
A.7.5×105 B.7.5×10﹣5 C.0.75×10﹣4 D.75×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:将0.000075用科学记数法表示为:7.5×10﹣5.
故选:B.
本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
3.(2分)如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( )
A. B.
C. D.
【分析】根据高线的定义即可得出结论.
【解答】解:A,C,D都不是△ABC的边AB上的高,
故选:B.
本题考查的是作图﹣基本作图,熟知三角形高线的定义是解答此题的关键.
4.(2分)下列等式从左到右的变形,属于因式分解的是( )
A.a(x﹣y)=ax﹣ay B.x3﹣x=x(x+1)(x﹣1)
C.(x+1)(x+3)=x2+4x+3 D.x2+2x+1=x(x+2)+1
【分析】根据因式分解的意义即可判断.
【解答】解:因式分解是指将一个多项式化为几个整式的乘积,
故选:B.
本题考查因式分解的意义,解题的关键是正确理解因式分解的意义,本题属于基础题型.
5.(2分)如果a=﹣0.32,b=﹣3﹣2,c=(﹣)﹣2,d=(﹣)0,那么a、b、c、d的大小关系为( )
A.a<b<c<d B.a<d<c<b C.b<a<d<c D.c<a<d<b
【分析】根据负整数指数幂、有理数的乘方、零指数幂的定义将a、b、c、d的值计算出来即可比较出其值的大小.
【解答】解:因为a=﹣0.32=﹣0.09,
b=﹣3﹣2=﹣=﹣,
c=(﹣)﹣2==9,
d=(﹣)0=1,
所以c>d>a>b.
故选:C.
本题主要考查了
(1)零指数幂,负整数指数幂和有理数的乘方运算:负整数指数为正整数指数的倒数;任何非0数的0次幂等于1.
(2)有理数比较大小:正数>0;0>负数;两个负数,绝对值大的反而小.
6.(2分)如果关于x的不等式2x+a>0的解集在数轴上表示如下图,那么a的值为( )
A.﹣2 B.2 C.﹣6 D.6
【分析】先根据在数轴上表示不等式解集的方法得出不等式的解集,再把a当作已知条件得出不等式的解集,与求出的不等式解集相比较即可.
【解答】解:∵由题意可知,不等式的解集为x>3,
解不等式2x+a>0得,x>﹣,
∴﹣=3,解得a=﹣6.
故选:C.
本题考查的是解一元一次不等式,熟知不等式的基本性质是解答此题的关键.
7.(2分)方程组中,若未知数x、y满足x+y>0,则m的取值范围是( )
A.m>﹣4 B.m≥﹣4 C.m<﹣4 D.m≤﹣4
【分析】①+②得出3x+3y=4+m,求出x+y=,根据x+y>0得出>0,再求出不等式的解集即可.
【解答】解:,
①+②,得3x+3y=4+m,
x+y=,
∵方程组中,未知数x、y满足x+y>0,
∴>0,
解得:m>﹣4,
故选:A.
本题考查了解二元一次方程组,二元一次方程组的解和解一元一次不等式等知识点,能求出关于m的不等式是解此题的关键.
8.(2分)已知是方程2x﹣ay=3的一个解,那么a的值是( )
A.1 B.3 C.﹣3 D.﹣1
【分析】把方程的解代入方程,把关于x和y的方程转化为关于a的方程,然后解方程即可.
【解答】解:∵是方程2x﹣ay=3的一个解,
∴满足方程2x﹣ay=3,
∴2×1﹣(﹣1)a=3,即2+a=3,
解得a=1.
故选:A.
本题主要考查了二元一次方程的解.解题关键是把方程的解代入原方程,使原方程转化为以系数a为未知数的方程.
9.(2分)下列式子一定成立的是( )
A.若ac2=bc2,则a=b
B.若ac>bc,则a>b
C.若a>b,则ac>bc2
D.若a<b,则a(c2+1)<b(c2+1)
【分析】根据不等式的性质进行判断即可.
【解答】解:A.若c=0,则ac2=bc2,
但a与b不一定相等,
则A不符合题意;
B.若ac>bc,c<0,
那么a<b,
则B不符合题意;
C.若a>b,c=0,
那么ac=bc2,
则C不符合题意;
D.若a<b,则c2+1>0,
那么a(c2+1)<b(c2+1),
则D符合题意;
故选:D.
本题考查不等式的性质,根据不等式的性质并结合反例进行判断是解题的关键.
10.(2分)已知方程组和有相同的解,则a,b的值为( )
A. B. C. D.
【分析】因为方程组和有相同的解,所以把5x+y=3和x﹣2y=5联立解之求出x、y,再代入其他两个方程即可得到关于a、b的方程组,解方程组即可求解.
【解答】解:∵方程组和有相同的解,
∴方程组的解也它们的解,
解得:,
代入其他两个方程得,
解得:,
故选:D.
本题主要考查了二元一次方程的解及二元一次方程组的解法,正确理解题意,然后根据题意得到关于待定系数的方程组,解方程组是解答此题的关键.
11.(2分)如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
【分析】根据平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行分别进行分析即可.
【解答】解:A、根据内错角相等,两直线平行可判断直线l1∥l2,故此选项不合题意;
B、∠2=∠3,不能判断直线l1∥l2,故此选项符合题意;
C、根据同位角相等,两直线平行可判断直线l1∥l2,故此选项不合题意;
D、根据同旁内角互补,两直线平行可判断直线l1∥l2,故此选项不合题意;
故选:B.
此题主要考查了平行线的判定,关键是掌握平行线的判定定理.
12.(2分)如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为( )
A.70° B.50° C.40° D.30°
【分析】延长ED交BC于F,根据平行线的性质求出∠MFC=∠ABC=70°,求出∠FDC=30°,根据三角形外角性质得出∠BCD=∠MFC﹣∠MDC,代入求出即可.
【解答】解:延长ED交BC于F,如图所示:
∵AB∥DE,∠ABC=70°,
∴∠MFC=∠ABC=70°,
∵∠CDE=140°,
∴∠FDC=180°﹣140°=30°,
∴∠BCD=∠MFC﹣∠MDC=70°﹣30°=40°,
故选:C.
本题考查了三角形外角性质,平行线的性质,解此题的关键是求出∠MFC的度数,注意:两直线平行,同位角相等.
13.(2分)我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
【分析】直接利用“绳长=木条+4.5;绳子=木条﹣1”分别得出等式求出答案.
【解答】解:设木条长x尺,绳子长y尺,那么可列方程组为:
.
故选:A.
此题主要考查了由实际问题抽象出二元一次方程组,正确得出等量关系是解题关键.
14.(2分)已知关于x的不等式组的整数解共有5个,则a的取值范围是( )
A.﹣3<a<﹣2 B.﹣3<a≤﹣2 C.﹣3≤a≤﹣2 D.﹣3≤a<﹣2
【分析】先求出每个不等式的解集,再求出不等式组的解集,根据已知得出关于a的不等式组,即可得出选项.
【解答】解:
∵解不等式①得:x≥a,
解不等式②得:x<3,
∴不等式组的解集为a≤x<3,
∵关于x的不等式组的整数解共有5个,
∴﹣3<a≤﹣2,
故选:B.
本题考查了解一元一次不等式组,不等式组的整数解的应用,解此题的关键是能根据不等式组的解集和已知得出关于a的不等式组.
15.(2分)如图,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC内,若∠2=80°,则∠1的度数为( )
A.20° B.30° C.40° D.无法确定
【分析】先根据三角形内角和定理求出∠C的度数,故可得出∠3+∠4的度数,根据四边形的内角和等于360°即可得出结论.
【解答】解:∵△ABC中,∠A=60°∠B=70°,∠2=80°,
∴∠C=180°﹣60°﹣70°=50°,
∴∠3+∠4=∠A+∠B=60°+70°=130°,
∴∠1=360°﹣(∠A+∠B)﹣(∠3+∠4)﹣∠2=360°﹣130°﹣130°﹣80°=20°.
故选:A.
本题考查的是三角形内角和定理及翻折变换,熟知图形翻折不变性的性质是解答此题的关键.
16.(2分)如图,在△ABC 中,点D、E、F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是( )
A.30 B.28 C.56 D.60
【分析】根据BD=2DC得出△BGD和△CGD面积之间的关系,根据E是AC的中点得出△AGE和△CGE面积之间的关系,从而求出△BCE的面积,再根据BE是△ABC的中线即可求出△ABC的面积.
【解答】解:∵BD=2DC,
∴S△BGD=2S△CGD=16,
∴S△CGD=8,
∵E是AC的中点,
∴S△AGE=S△CGE=6,
∴S△BCE=S△BGD+S△CGD+S△CGE
=16+8+6
=30,
∵E是AC的中点,
∴S△ABC=2S△BCE=2×30=60,
故选:D.
本题考查了三角形面积的求法,熟知三角形的中线把三角形分成两个面积相等的三角形.
二、填空题(共4小题,17-19题每题3分,20题每空2分,共13分)
17.(3分)因式分解:a2﹣2ab+b2﹣1= (a﹣b+1)(a﹣b﹣1) .
【分析】先将该多项式分组,再运用公式法进行因式分解.
【解答】解:a2﹣2ab+b2﹣1
=(a2﹣2ab+b2)﹣1
=(a﹣b)2﹣12
=(a﹣b+1)(a﹣b﹣1),
故答案为:(a﹣b+1)(a﹣b﹣1).
此题考查了运用分组法和公式法进行因式分解的能力,关键是能准确确定分解方法.
18.(3分)自来水公司为某小区A改造供水系统,如图沿路线AO铺设管道和BO主管道衔接(AO⊥BO),路线最短,工程造价最低,根据是 垂线段最短 .
【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.据此作答.
【解答】解:根据是:直线外一点与直线上各点连接而得到的所有线段中,垂线段最短.
故答案为:垂线段最短.
此题主要考查垂线段最短在实际生活中的应用.
19.(3分)如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数 60° .
【分析】由垂直的定义,角平分线的定义以及三角形内角和定理进行计算即可.
【解答】解:∵AD⊥BC,
∴∠ADB=90°,
∵∠B=50°,
∴∠BAD=90°﹣50°=40°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=40°﹣5°=35°,
∴∠BAC=2×35°=70°,
∴∠C=180°﹣50°﹣70°
=60°,
故答案为:60°.
本题考查三角形内角和定理,角平分线以及垂直的定义,掌握三角形内角和是180°,角平分线的定义是正确解答的前提.
20.(4分)在△ABC中,∠A=160°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图①,则∠A1的度数为 140° ;第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图②.照此下去,至多能进行 7 步.
【分析】根据三角形内角和是180°,推出另外两角之和,依次类推可得出规律,依据三角形角不能为0,推出进行的步数即可.
【解答】解:∵∠A=160°,
∴∠ABC+∠ACB=180°﹣∠A=20°,
∵∠A1BA=∠ABC,∠A1CA=∠ACB,
∴∠A1BC+∠A1CB=2(∠ABC+∠ACB)=40°,
∴∠A1=180°﹣(∠A1BC+∠A1CB)=140°,
同理∠A2=120°,
∠A3=100°,
……
∠An=180°﹣20(n+1),
∴当n=8时,∠A8=0,
∴至多能进行七步.
故答案为:140°,7.
本题考查了三角形的内角和定理,三角形内角和是180°,知道一个角的度数,可以求出另外两角和的度数.
三、解答题(本大题共6个大题,共55分,解答应写出文字说明、证明过程或演算步骤)
21.(10分)(1)解方程组:;
(2)解不等式组并写出不等式组的整数解.
【分析】(1)利用加减消元法求解即可;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集,即可求出整数解.
【解答】解:(1)①×2+②,得:11x=22,
解得x=2,
将x=2代入①,得:8﹣y=5,
解得y=3,
∴方程组的解为;
(2)解不等式+3≥x,得:x≤3,
解不等式1﹣2(x﹣1)<4﹣x,得:x>﹣1,
则不等式组的解集为﹣1<x≤3,
所以不等式组的整数解为0,1,2,3.
本题考查的是解二元一次方程组和一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
22.(10分)(1)先化简,再求值:a(a﹣3b)+(a+b)2﹣a(a﹣b)其中a=1,.
(2)是小明完成的一道作业,请你参考小明的方法解答下面的问题:
小明的作业计算:85×(﹣0.125)5 解:85×(﹣0.125)5=(﹣8×0.125)5 =(﹣1)5 =﹣1
①42020×(﹣0.25)2020;
②;
③若 2×4n×16n=219,直接写出n的值.
【分析】(1)先展开,再去括号,合并同类项,化简后将a,b的值代入计算即可;
(2)①逆用积的乘方法则可得答案;
②逆用积的乘方法则;
③化为同底数,可得关于n的方程,即可解得答案.
【解答】解:(1)原式=a2﹣3ab+a2+2ab+b2﹣a2+ab
=a2+b2,
当a=1,b=﹣时,
原式=12+(﹣)2
=1+
=;
(2)①42020×(﹣0.25)2020
=[4×(﹣0.25)]2020
=(﹣1)2020
=1;
②原式=[×(﹣)×]11×(﹣)2×
=(﹣1)11××
=﹣1××
=﹣;
③∵2×4n×16n=219,
∴2×22n×24n=219;
∴26n+1=219;
∴6n+1=19,
解得n=3,
∴n的值为3.
本题考查整式的混合运算,解题的关键是掌握整式相关运算的法则.
23.(7分)边长为b的小1,从边长为a的大正方形中剪掉一个【探究】如图1方形,将阴影部分沿虚线剪开,拼成图2的长方形.
(1)请你分别表示出这两个图形中阴影部分的面积:图1 a2﹣b2 ,图2 (a+b)(a﹣b) .
(2)比较两图的阴影部分面积,可以得到乘法公式: 1 (用字母a,b表示).
【应用】请应用这个公式完成下列各题:
①已知2m﹣n=3,2m+n=4,则4m2﹣n2的值为 12 ;
②计算:(x﹣3)(x+3)(x2+9).
【拓展】计算(2+1)(22+1)(2++1)(22+1)…(232+1)的结果为 264﹣1 .
【分析】(1)图①阴影部分的面积为两个正方形的面积差,即a2﹣b2,而图②的阴影部分为长为(a+b),宽为(a﹣b)的矩形,可表示出面积为(a+b)(a﹣b).
(2)由图①与图②的面积相等,可以得到乘法公式;
①利用公式将4m2﹣n2写成(2m﹣n)(2m+n)进而求出答案.
②连续两次利用平方差公式进行计算即可.
将原式转化为(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1),再连续使用平方差公式,得出最后的结果.
【解答】解:【探究】(1)图①阴影部分的面积为两个正方形的面积差,即a2﹣b2;图②的阴影部分为长为(a+b),宽为(a﹣b)的矩形,其面积为(a+b)(a﹣b).
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)由图①与图②的面积相等,可以得到乘法公式,(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b);(a﹣b)=a2﹣b2;
【应用】①4m2﹣n2=(2m﹣n)(2m+n)=3×4=12.
故答案为:12.
②(x﹣3)(x+3)(x2+9)=(x2﹣9)(x2+9)=x4﹣81;
【拓展】(2+1)(22+1)(24+1)(28+1)…(232+1),
=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1),
=(22﹣1)(22+1)(24+1)(28+1)…(232+1),
=(24﹣1)(24+1)(28+1)…(232+1),
=(28﹣1)(28+1)…(232+1),
=264﹣1.
故答案为:264﹣1.
考查平方差公式,掌握平方差公式的结构特征是正确应用的前提.
24.(8分)已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
(1)猜想:DC与AB的位置关系,并说明理由.
(2)求∠AFE的大小.
【分析】(1)由AD∥BC,得到∠CBF=∠DAB,而∠DCB=∠DAB,因此∠CBF=∠DCB,即可证明CD∥AB;
(2)由DC∥AB,得到∠EAF=∠DEA=30°,由直角三角形的性质得到∠AFE=90°﹣∠EAF=60°.
【解答】解:(1)CD∥AB,理由如下:
∵AD∥BC,
∴∠CBF=∠DAB,
∵∠DCB=∠DAB,
∵∠CBF=∠DCB,
∴CD∥AB;
(2)∵DC∥AB,
∴∠EAF=∠DEA=30°,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AFE=90°﹣∠EAF=60°.
本题考查平行线的判定和性质,熟练掌握平行线的判定和性质是解题的关键.
25.(10分)某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需资金1020元;若购买甲种书柜44个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜的单价分别是多少?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请你帮助学校设计可以选择的购买方案.
【分析】(1)设每个甲种书柜的价格是x元,每个乙种书柜的价格是y元,根据“若购买甲种书柜3个,乙种书柜2个,共需要资金1020元;若购买甲种书柜4个,乙种书柜3个,共需要资金1440元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买m个甲种书柜,则购买(20﹣m)个乙种书柜,根据“乙种书柜的数量不少于甲种书柜的数量,且学校至多能提供资金4320元”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数,即可得出各购买方案.
【解答】解:(1)设每个甲种书柜的单价是x元,每个乙种书柜的单价是y元,
依题意得:,
解得:.
答:甲种书柜的单价是180元,乙种书柜的单价是240元.
(2)设购买m个甲种书柜,则购买(20﹣m)个乙种书柜,
依题意得:,
解得:8≤m≤10,
又∵m为整数,
∴m可以取8,9,10,
∴该校共有3种购买方案,
方案1:购买8个甲种书柜,12个乙种书柜;
方案2:购买9个甲种书柜,11个乙种书柜;
方案3:购买10个甲种书柜,10个乙种书柜.
本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
26.(10分)已知∠MON=90°,点A,B分别在射线OM,ON上运动(不与点O重合)
观察:
(1)如图1,若∠OBA和∠OAB的平分线交于点C,∠ACB= 135 °
猜想:
(2)如图2,随着点A,B分别在射线OM,ON上运动(不与点O重合).若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E,∠E的大小会变吗?如果不会,求∠E的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将△ABE沿MN折叠,使点E落在四边形ABMN内点E′的位置.求∠BME′+∠ANE′的度数.
【分析】(1)根据三角形的内角和定理角平分线的定义计算即可.
(2)利用三角形的外角的性质,三角形内角和定理构建关系式解决问题即可.
(3)根据翻折不变性,三角形内角和定理,三角形的外角的性质构建关系式解决问题即可.
【解答】解:观察:(1)∵∠MON=90°,
∴∠OAB+∠OBA=90°,
∵∠OBA和∠OAB的平分线交于点C,
∴∠ABC=∠OBA,∠BAC=∠OAB,
∴∠ABC+∠BAC=(∠OBA+∠OAB)=45°,
∴∠CBA=180°﹣45°=135°
故答案为135.
猜想:(2)∵AE是∠BAO的平分线
∴∠BAE=∠BAO,
∵BC是∠ABN的平分线,
∴∠CBA=∠NBA,
∵∠NBA=∠O+∠BAO,
∴∠CBA=(∠O+∠BAO)=45°+∠BAE,
∵∠CBA=∠E+∠BAE,
∴∠E+∠BAE=45°+∠BAE,
即∠E=45°.
拓展:(3)由折叠可得,∠EMN=∠E′MN,∠E N M=∠E′NM,
∴2∠EMN+∠BM E′=180°,2∠ENM+∠ANE′=180°,
∴∠BM E′=180°﹣2∠EMN,∠ANE′=180°﹣2∠ENM,
∴∠BM E′+∠ANE′=360°﹣2(∠EMN+∠ENM),
∵∠EMN+∠ENM=180°﹣∠E,∠E=45°,
∴∠BM E′+∠ANE′=360°﹣2(∠EMN+∠ENM)
=360°﹣2(180°﹣∠E)
=2∠E
=90°.
本题考查三角形内角和定理,三角形的外角的性质,翻折变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
同课章节目录
